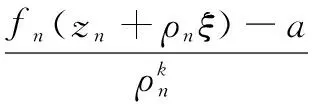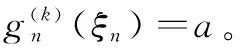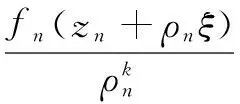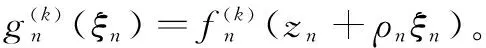涉及高阶导数分担值的亚纯函数正规族
2017-11-02吕凤姣刘芝秀
吕凤姣,刘芝秀
(1.黄河科技学院信息工程学院,郑州450063;2.南昌工程学院理学院,南昌330099)
涉及高阶导数分担值的亚纯函数正规族
吕凤姣1,刘芝秀2
(1.黄河科技学院信息工程学院,郑州450063;2.南昌工程学院理学院,南昌330099)
正规族理论的发展经历了利用Nevanlinna值分布理论和L.Zalcman引理简化许多通过大量消去原始值而得到正规定则证明的过程,同时也建立了一系列新的正规定则。把亚纯函数正规族与分担值或分担集合结合起来考虑是亚纯函数正规族理论研究的一个重要课题。目前正规族的相关理论在复动力系统、复微分方程、模分布和整函数唯一性等方面都有着重要的应用。文章主要探讨了亚纯函数的值分布理论,利用L.Zalcman引理研究了一类涉及高阶导数分担值的亚纯函数族的正规性问题,推广并改进了已有的结果。主要结果为:设F是区域D上的一亚纯函数族,k为正整数,a为非零有穷复数,若对任意的f(z)∈F,有f(z)-a的零点重级至少为k+1,且f(z),f(k)(z)与f(k+1)(z)IM分担a,则F在D上正规。
亚纯函数;高阶导数;分担值;正规族
引言
设f(z)为开平面上非常数的亚纯函数,采用值分布论中的相关记号[1-2],在此给出相关的定义。
设D为复平面C上的区域,F为定义在区域D内一族亚纯函数,称F在区域D上正规,是指亚纯函数族F中每一个函数序列{fn(z)}(n=1,2,…)均可以选出一个子序列{fnk(z)}(k=1,2,…)在区域D上按球面距离内闭一致收敛于一个亚纯函数或者恒为无穷。
称F在区域D上一点z0正规是指,F在z0的某个领域内正规。可知,F在区域D上正规等价于F在区域D上每一点都正规。
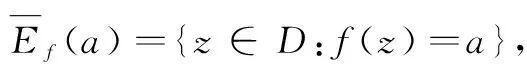
设f(z),g(z)为区域D上的两个亚纯函数,对复数a∈C,若f(z)-a的零点为zn(n=1,2,3,…),如果zn(n=1,2,3,…)也是g(z)-a的零点(不计重数),则称单向分担a,记为f(z)=a⟹g(z)=a。
把亚纯函数正规族与分担值或分担集合结合起来考虑是由W.schwick在1992年首先开始研究,之后国内外许多学者都对这方面进行了深入的研究,其成果有:
定理1[3]设F={f(z)}是单位圆盘Δ上的亚纯函数族,a1,a2,a3是三个不同的复数,如果对每个f∈F,f与f′同时分担值a1,a2,a3,则F在Δ上正规。
定理2[4]设F是D上的一亚纯函数族,a和b是两个不同的复数,如果对任一f∈F,f(z)与f′(z)在D内IM分担a,b,则F在D内正规。
定理3[5]设F是区域D上的解析函数族,a和b是两个相互判别的非零有穷复数,如果对∀f∈F,有f(z)=a⟺f′(z)=a,f′(z)=b⟺f″(z)=b,那么F在D内正规。
文献[5]在定理3的后面,提出一个问题:该定理对亚纯函数族是否成立?
2013年,文献[6]将解析函数族推广为亚纯函数族,并将f′推广为f(k),得到了如下两个结论。
定理4设F是区域D上的亚纯函数族,且a和b是两个相互判别的非零有穷复数,如果对∀f∈F,f(z)的零点重级至少为2,且f(z)=a⟺f′(z)=a,f′(z)=b⟺f″(z)=b,那么F正规。
定理5设F是区域D上的亚纯函数族,且a和b是两个相互判别的非零有穷复数,k是一个正整数。如果对∀f∈F,f(z)的零点重级至少为k+1,且f(z)=a⟺f(k)(z)=a,f(k)(z)=b⟺f(k+1)(z)=b,那么F在D内正规。
但是,在上述定理中有两个分担值,能否把f′推广为f(k)的同时,将分担值的个数减少为一个呢?本文证明了下述定理。
定理6设F是区域D上的一亚纯函数族,k为正整数,a为非零有穷复数,若对任意的f(z)∈F,有f(z)-a的零点重级至少为k+1,且f(z),f(k)(z)与f(k+1)(z)IM分担a,则F在D上正规。
文献[7-8]举例说明了定理中的条件“函数的零点重级至少为k+1”是必须的,此例也说明了定理6中的条件“f(z)-a的零点重级至少为k+1”是必须的。
1 引理
引理1[9](Zalcman引理)设k为正整数,F是单位圆盘Δ上的亚纯函数族,f的零点重级均≥k,极点重级均≥j,那么F在Δ上不正规的充要条件是:对∀α∈(-j,k),存在函数列fn∈F,点列zn∈Δ,正数列ρn→0,使得函数列
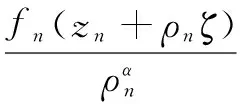
在复平面上按球距内闭一致地成立。
这里g(ζ)为复平面上的一个亚纯函数,其零点(极点)重级均≥k(j),且g#(ζ)≤g#(0)=1。
注这是Zalcman引理的推广,亦称为Zalcman引理,其中,当k=1,j=1,α=0时是Zalcman最先的结果。上面的形式是经庞学诚[10],Schwick[11],陈怀惠和顾永兴[12]推广而得到的。
本文常用的Zalcman引理是庞学诚和Zalcman对上面的结果所做的进一步的推广。
引理2[13](Pang-Zalcman引理)设k为正整数,F是单位圆盘Δ上的亚纯函数族,f的零点重级至少为k,假设存在A≥1,使得当f(z)=0时,有|f(k)(z)|≤A对∀f∈F都成立。如果F在单位圆内不正规,则对0≤α≤k,存在正数r,0 在复平面上按球距内闭一致地成立。这里g(ζ)为复平面上的一个非常数亚纯函数,其零点重级至少为k,且g#(ζ)≤g#(0)=kA+1。特别地,g(ζ)的级至多为2。 引理3[14]设函数序列{fn(z)}在区域D内解析,并且在D内闭一致收敛到一个不恒为零的函数,γ是D内可求长的闭曲线,其内部属于D,且不经过f(z)的零点,则存在正整数N,使得当n≥N时,在γ内部,fn(z)和f(z)的零点个数是相同的。 引理4[15-16](Hayman不等式)设f(z)是一个亚纯函数,a为非零复数,k为正整数。若f(z)≠0,f(k)(z)≠a,则f(z)是一个常数。 证明假设F在D上不正规,不失一般性,由引理2得: 按球面距离内闭一致收敛,这里g(ξ)是复平面C上的非常数亚纯函数,且满足g(k)(ξ)≤g(k)(0)=k(|a|+1)+1。 证明g(k)(ξ)≠a,g(ξ)≠0。先证g(k)(ξ)≠a。 所以ξ0是g(k)(ξ)的a-值点,是重级的。 假定ξ0是g(k)(ξ)的l重a-值点(l≥2),则g(k+l)(ξ0)≠0,从而存在δ>0,当|ξ-ξ0|<δ时,有 g(k+l)(ξ)≠0 (1) 所以这l个a-值点均是单级的。即当i≠j时,ξni≠ξnj。所以g(k+l)(ξ0)=0,这与式(1)矛盾。 因此g(k)(ξ)≠a得证。 再证g(ξ)≠0。 假设存在ξ0,使g(ξ0)=0。由Hurwitz定理,存在ξn,ξn→ξ0,当n充分大时,有 根据引理4得,g(ξ)是一个常数。这与假设相矛盾。从而定理6得证。 目前,正规族的相关理论在复动力系统、复微分方程、模分布和整函数唯一性等方面都有着广泛的应用。另外,将正规族理论应用到亚纯函数唯一性的研究中,已取得了一些很好的结果。 [1] 杨乐.值分布论及其新研究[M].北京:科学出版社,1982. [2] LIU X J,LI S H,PANG X C.A normal criterion about two families of meromorphic functions concering shared values[J].Acta Mathematica Sinica,English Series,2013(1):151-158. [3] SCHWICK W.Sharing values and normality[J].Arch Math,1992,59:50-54. [4] PANG X,LAWRENCE Z. Normality and shared values[J].Arkiv for Matematik,2000,38:171-182. [5] 顾永兴,庞学诚,方明亮.正规族理论及其应用[M].北京:科学出版社,2007. [6] 段曦盛,谢莉.分担值与亚纯函数的正规性[J].数学物理学报,2013,33A(2):242-245. [7] ZHANG G M,PANG X C,ZALCMAN L.Normal families and omitted functions II[J].Bull London Math Soc,2009,41:63-71. [8] 王雪琴.亚纯函数的分担值与正规族[J].数学物理学报,2014,34A(4):1008-1013. [9] ZALCMAN L.A heuristic principle in complex function theory[J],Ame Math Mont,1975(82):813-817. [10] PANG X.Blochs principle and normal criterion[J].Sci China Ser A,1989(32):782-791. [11] SCHWICK W.Normality Crietion for families of meromorphic functions[J].Anal Math,1989,52:241-289. [12] 陈怀惠,顾永兴.Marty定则的改进及应用[J].中国科学A辑,1993,23(2):123-129. [13] 庞学诚.亚纯函数的正规族与正规函数[J].数学年刊A辑,2000(5):601-604. [14] 方企勤.复变函数教程[M].北京:北京大学出版社,1996. [15] HAYMAN W K.Picard Value of Meromorphe functions And Their Derivatives[J].Annals of Mathematics,1959,70:9-42. [16] LI S,GAO Z.Results on a question of Zhangand Yang[J].Acta Math Sci Ser B Engl Ed,2012,32:717-723. NormalFamiliesofMeromorphicFunctionsInvolvingHigherDerivativeSharingValues LVFengjiao1,LIUZhixiu2 (1.Collge of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450063, China;2.College of Science, Nanchang Institute of Technology, Nanchang 330099, China) The development of the normal family theory has undergone the process of using Nevanlinna value distribution theory and L.Zalcman lemma to simplify many formal rules proving that large numbers of original values are eliminated. A series of new normal rules are also established. It is an important subject for the study of the normal family theory of meromorphic functions to combine the normal families of meromorphic functions with the shared values or the shared set. At present, the theory of normal families have important applications in complex dynamical systems, complex differential equations, module distribution and the uniqueness of entire functions. The value distribution theory of meromorphic functions is mainly discussed, and the normality of meromorphic functions related to higher order derivative sharing values is studied by using the L.Zalcman lemma, which improved the existing results. Main results are as follows: LetFis families of meromorphic functions onD.Letkis a positive integer andais non-zero finite complex number. If for everyf∈F, zero magnitude off(z)-aof at leastk+1, andf(z),f(k)(z) andf(k+1)(z) share a with IM, thenFis normal onD. meromorphic function; higher derivative; shared values; normal family O174.52 A 2017-07-12 国家自然科学基金项目(U1304102);郑州市科技局基金项目(20141375);南昌工程学院青年基金项目(2014KJ025) 吕凤姣(1983-),女,河南商丘人,讲师,主要从事复分析方面的研究,(E-mail)lvfengjiao_2008@163.com 1673-1549(2017)05-0079-04 10.11863/j.suse.2017.05.14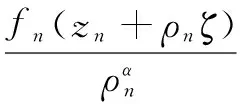
2 定理6的证明