城市宜居程度的一个评价模型

卢天秀，唐浩，刘美君，刘玲，杨勇

(四川理工学院数学与统计学院，四川自贡643000)

城市宜居程度的一个评价模型

卢天秀，唐浩，刘美君，刘玲，杨勇

(四川理工学院数学与统计学院，四川自贡643000)

针对宜居城市评价指标问题，在合理的假设条件下，采用理论分析法和频度统计法筛选出主要指标(包括5个一级指标和8个二级指标)，利用熵值法建立了评价宜居城市的数学模型。然后以8个城市为例，计算出一级指标和二级指标的权重，以及每个二级指标的熵值，从而给出8个城市综合得分排名。最后，得出生态环境和文化教育这两个指标的变化会对宜居城市排名产生显著的影响。

频度统计法；熵值法；主成分分析法；KMO值(Kaiser-Meyer-Olkin值)；模糊物元模型

引言

城市宜居性是当前城市科学研究领域的热点议题之一，也是政府和城市居民密切关注的焦点，对提升城市居民生活质量、完善城市功能和提高城市运行效率具有重要意义[1]。

我国宜居城市的排名每年都是热门话题，评价指标体系不同，宜居城市排名结果也会发生变化。2016年，中科院发布了《中国宜居城市研究报告》[2]，在被调查的40个城市中，排名前十的城市分别为：青岛、昆明、三亚、大连、威海、苏州、珠海、厦门、深圳、重庆。而美世人力资源咨询公司(William Mercer)公布的2016年全球宜居城市排行中大陆前十名分别为上海、北京、广州、成都、南京和深圳(并列)、西安、重庆、青岛、沈阳、吉林。

人们选择留在某个城市，不单是为了生存，更是寄托了自己的梦想与希望。对大多数人，衡量是否宜居或许就是八个字：衣食住行、安居乐业。

本文筛选出评价宜居城市的5个一级指标，8个二级指标，建立评价宜居城市的数学模型，对淮海经济区内的8个城市(宿迁、连云港、宿州、商丘、济宁、枣庄、徐州、淮北)进行合理性研究，给出宜居城市排名。

1 模型的建立

首先，假设获得的数据全部真实可靠，且取自同一个正态总体。评价宜居城市的各个指标之间的相互作用关系可以忽略不计。

根据文献[3]以及2007年5月30日正式发布的《宜居城市科学评价标准》(该文件是由科学研究会研究编订，并通过建设部科技司组织评审验收，具有一定的权威性)，选取的主要指标见表1。

表1 主要指标

表1中的五个一级指标基本概括了城市宜居的条件[4]。人均GDP是衡量经济指标的总量，反映了一个城市的经济发展情况，城镇居民可支配收入反映了人们的生活水平，因此选取“x1”和“x2”两个二级指标反映经济发展；绿化和卫生直接体现了城市生态改善强度，所以选取“x3”和“x4”两个二级指标反映生态环境[5]；x5是大多数国家和城市反映居住条件的指标；一个城市整体的文明程度，可以用教育发展的状况体现，所以选择“x6”直观体现文化教育这一指标；最低生活保障、失业率和广大基层人民的生活息息相关，因此选取“x7”和“x8”反映社会保障情况[6]。

应用熵值法建立宜居城市评分模型，熵值法能够深刻反映出指标信息熵值的效用价值，适合对多元指标进行综合评价。运用熵值法可克服多指标变量间的信息重叠和人为确定权重的主观性[7-9]。

主要步骤：

(1)选取n个城市，m个指标，则Xij为第i个城市的第j个指标的值(i=1,2,…,n；j=1,2,…,m)。

(2)指标的标准化处理：异质指标同质化。由于各项指标的计量单位并不统一，因此在计算综合指标前，先要对其进行标准化处理，即把指标的绝对值转化为相对值，并令Xij=|Xij|，从而解决各项不同指标值的同质化问题。而且，由于正向指标和负向指标数值代表含义不同(正向指标数值越高越好，负向指标数值越低越好)，因此，对于高低指标用不同的算法进行数据标准化处理。

正向指标：

(1)

负向指标：

(2)

(3)计算第j项指标下第i个城市占该指标的比重Pij：

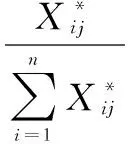
(3)

其中，i=1,2,…,n；j=1,2,…,m。

(4)计算第j项指标的熵值ej：

(4)

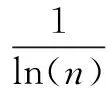
(5)计算第j项指标的差异性系数dj：

dj=1-ej

(5)

dj越大，第j项指标越重要。

(6)计算各项指标的权重wj：

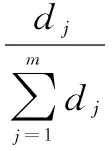
(6)

(7)构建指标综合评价模型f(i)：

(7)

由此模型，可以得到第i个城市的综合得分。

2 八个宜居城市排名

用y1,y2,…,y8分别代表宿迁、连云港、宿州、商丘、济宁、枣庄、徐州和淮北8个市，根据《中国城市统计年鉴》、《中国民政统计年鉴》、以及江苏、安徽、山东、河南省的统计年鉴，2015年8个城市关于8个二级指标x1,x2,…,x8的数据矩阵为：

x1x2x3x4x5x6x7x8

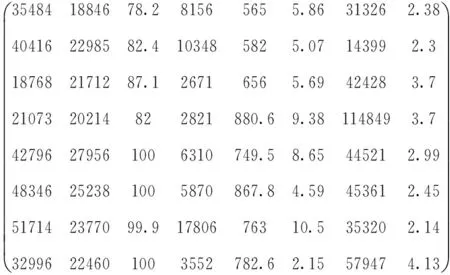
可计算出每列的平均数为：

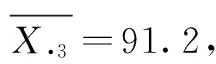
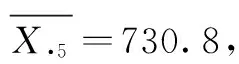
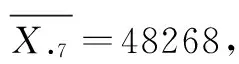
原始数据矩阵可知y2(连云港市)和y7(徐州市)的大部分正向指标高于平均数，负向指标均低于平均数。商丘的正向指标明显偏低，负向指标偏高，特别是城镇居民低保人数远高于平均数。

按照熵值法建立的模型确定6个正向二级指标：x1，x2，x3，x4，x5，x6；2个负向二级指标：x7，x8，按照正向指标的标准化公式(1)与负向级指标的标准化公式(2)进行处理，并计算：

(1)对标准化后的数据，按照熵值法步骤中式(3)、式(4)和式(5)得到熵值ej、差异性系数dj：

ejdj

(2)按式(6)计算一级指标的权重为：

w(H1)=0.105695968

w(H2)=0.369539735

w(H3)=0.0223169130

w(H4)=0.159732078

w(H5)=0.0.342715307

二级指标的权重为：

w1=0.09311762

w2=0.012578348

w3=0.009265406

w4=0.360274329

w5=0.022316913

w6=0.159732078

w7=0.292404612

w8=0.050310695

(3)运用综合评价模型式(7)，得到8个城市的一级指标分数矩阵为：

H1H2H3H4H5

从而，淮海经济区8个城市综合得分和排名为：

Score(y7)=0.822；Score(y2)=0.732

Score(y1)=0.535；Score(y5)=0.508

Score(y6)=0.455；Score(y4)=0.343

Score(y3)=0.338；Score(y8)=0.302

3 指标显著性分析

在建立的评价模型中，不同指标对于权重的影响不同，需要分析其中哪些是重要指标，这里选择主成分分析法，通过保留低阶主成分，忽略高阶主成分达到减少数据集的维数，同时保持数据中对方差贡献最大的那些特征[10-11]。

将原始数据在SPSS软件中进行因子分析，得到x1，x2，x3，x4，x5，x6，x7，x8的相关矩阵：

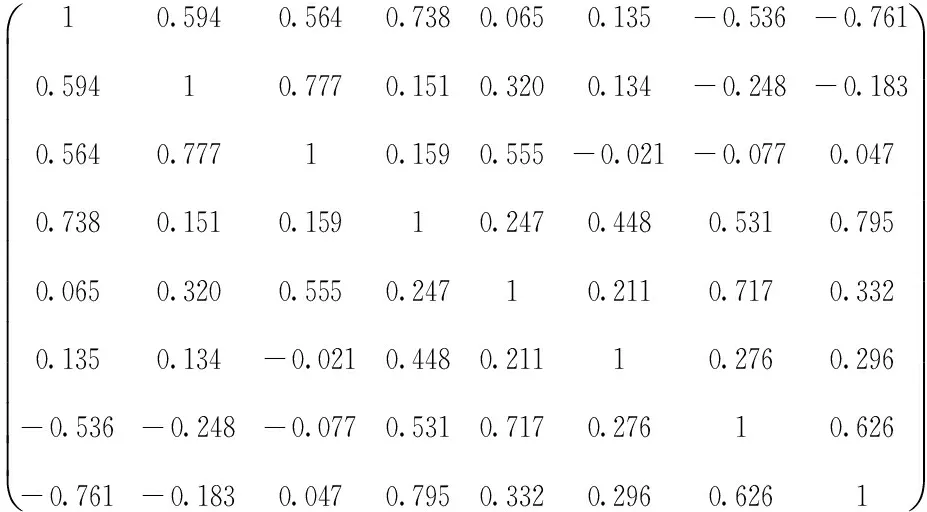
此矩阵不是正定矩阵，而且没有产生KMO检验值。原因主要可能集中在两点：(1)样本量太少，而指标过多；(2)某些变量间的相关性太强；没有产生KMO值的情况可能是两个以上指标为纯线性关系。

这里不可能增加样本，故只能从指标间的相关性考虑。通过查看相关矩阵，大部分变量存在相关性，故需要删除高度相关的指标。利用逐一淘汰法找到了5个指标：x1，x4，x6，x7，x8，得出相关矩阵：

KMO检验和Bartlett检验结果见表2。

表2 KMO检验和Bartlett检验

KMO值大于0.6，说明可以进行因子分析。碎石图(图1)横轴表示指标的序号，纵轴代表特征根。

图1 碎石图

由图1可知：随着指标序号增大，特征根迅速降低，后两个指标的特征根变化非常小，所以认为得到两个因子比较合适。从而得到成份矩阵R1：

成分1 成分2

具有Kaiser标准化的斜交旋转法，在5次迭代后收敛，模式矩阵R2：

成分1 成分2

最后得到结构矩阵R3：

成分1 成分2

由成分矩阵R1、模式矩阵R2和结构矩阵R3可得：第一公因子在指标x4数据上具有最大的载荷，第二公因子在x6数据上具有最大的载荷。x4属于第一指标H2，x6属于第一指标H4，所以，得出生态环境和文化教育的变化会对宜居城市的排名产生显著的影响。

4 结果检验

本文得出的城市宜居程度排名：徐州市、连云港市、宿迁市、济宁市、枣庄市、商丘市、宿州市、淮北市。根据2015年8个城市二级指标值原始数据矩阵，徐州市的全部正向指标数据均高于平均数，负向指标数据均低于平均数，连云港市的大部分正向指标高于平均数，且其差值不大，负向指标均低于平均数；而淮北市的各项指标在8个城市中都偏低，且大部分正向指标都低于平均数，负向指标均高于平均数，所以说徐州排名第一，连云港市排名第二，淮北排名靠后是合理的，由此确定本文的排名是基本合理的。当然，使用模糊物元模型解决实际问题时，由于选取的指标和使用的数学方法不同，或者原始数据的准确性等因素的影响，可能会影响模型的可靠性[12-15]。在本文讨论的问题中，人们对评价宜居城市的标准具有不同的认识，而且选取的指标不一定非常全面，有的代表性指标因为数据限制而没有选取，所以排名结果并不绝对。

[1] 石永林,王要武.建设可持续发展生态城市的研究[J].中国软科学,2003(8):122-126.

[2] 中科院.中国宜居城市研究报告[M].北京:社会科学文献出版社,2016.

[3] 周维,张小斌,李新.我国人居环境评价方法的研究进展[J].安全与环境工程,2013,20(2):14-18.

[4] 尹东旭.内蒙古城市人居环境质量空间差异评价研究[D].内蒙古:内蒙古师范大学,2016.

[5] 张晓,戴菲.基于POE模式的街旁绿地规划设计研究:以武汉市为例[J].规划师论丛,2010(1):1-4.

[6] 毛通.城乡社会保障一体化评价体系研究及实证分析[J].社会保障研究,2012(1):15-27.

[7] 薛丽芳,欧向军,谭海樵.基于熵值法的淮海经济区城市中心性评价[J].地理与地理信息科学,2009,25(3):63-66.

[8] 李杰,陈璐.基于熵值法的上市公司绩效评价模型构建:以有色金属行业为例[J].财会通讯,2014(14):25-27.

[9] 刘娜,艾南山,方艳,等.基于熵权的模糊物元模型在城市生态系统健康评价中的作用[J].成都理工大学学报:自然科学版,2017(5):589-595.

[10] 李莉娟,张娜.关于主成分分析的几种常用改进方法[J].统计与咨询,2007(21):167-168.

[11] 黄俐,梁鹏.基于因子分析的地铁盾构施工沉降风险辨识[J].内蒙古大学学报:自然科学版,2016(2):209-216.

[12] JUN J F,LING Y Z,YU S C,et al.Health evaluation of a regional logistics industrial ecosystem in China based on fuzzy matter-element analysis method[J].Journal of Intelligent & Fuzzy Systems,2016,31(4):2195-2202.

[13] 宁宝权,陕振沛.基于改进熵和灰关联分析的模糊物元分析模型及应用[J].数学的实践与认识,2016,46(20):280-284.

[14] GUO Q X,TIAN T L,MING X S.Evaluation analysis for sortie generation of carrier aircrafts based on nonlinear fuzzy matter-element method[J].Journal of Intelligent & Fuzzy Systems,2016,31(6):3055-3066.

[15] ZHENG X G,JIAN G Y.Fuzzy Matter-Element Evaluation Method for Reliability Analysis of an Existing Highway Tunnel[J].Advanced Materials Research,2011,1067(163):3110-3113.

AnEvaluationModelontheDegreeofUrbanLivability

LUTianxiu,TANGHao,LIUMeijun,LIULing,YANGYong

(School of Mathematics and Statistics, Sichuan University of Science & Engineering, Zigong 643000,China)

Aiming at the evaluation index of urban livability, based on the reasonable assumptions, by theoretical analysis and frequency statistics, the main indexes (including five first-level indicators and eight second-level indexes) were selected. Using the entropy method, mathematical model of urban livability is carried out. Then, taking the eight cities as examples, the weight of the primary indexes and the secondary indexes, the entropy of secondary indexes are calculated. So the overall score ranking of the eight cities is given. Finally, it is obtained that the changes in the eco-environment and cultural education have significant impact on the degree of urban livability.

frequency statistics; entropy method; principal component analysis; Kaiser-Meyer-Olkin value; fuzzy matter-element model

O29；O24；O213

A

2017-08-11

国家自然科学基金(11501391)；人工智能四川省重点实验室开放基金项目(2015RZJ01)；桥梁无损检测与工程计算四川省高校重点实验室开放基金项目(2014QZJ02)；四川理工学院教学改革研究项目(JG-1708；JG-1102)

卢天秀(1976-)，女，四川自贡人，教授，博士，硕士生导师，主要从事拓扑动力系统，混沌理论及其应用方面的研究，(E-mail)lubeeltx@163.com

1673-1549(2017)05-0090-05

10.11863/j.suse.2017.05.16