水下双层圆柱壳辐射声场欠定分离评估方法研究

关珊珊，吴书有，陶襄樊，陈美霞，曹为午

（1.武汉第二船舶设计研究所，武汉 430064；2.华中科技大学，武汉 430070）

水下双层圆柱壳辐射声场欠定分离评估方法研究

关珊珊1，吴书有1，陶襄樊1，陈美霞2，曹为午1

（1.武汉第二船舶设计研究所，武汉 430064；2.华中科技大学，武汉 430070）

水下双层加筋圆柱壳振动和辐射声场的评估对其辐射噪声监测和控制具有重要工程意义。文中通过结构振动模态参与因子向量自身的稀疏特性，分析提出了一种基于结构振动的辐射噪声欠定分离评估方法，可实现有限振动测点情况下的水下复杂结构振动和辐射声场的有效评估。数值和试验结果验证了文中方法的有效性，且所需要的振动测点数目少，具有良好的工程适用性。

声场评估；欠定分离；水下双层加筋圆柱壳；振动测点

0 引 言

围绕弹性结构振动和辐射声场评估这一问题，国内外学者进行了广泛而深入的研究。目前主要的评估方法大致可分为基于模态、基于近场声全息以及基于物理声学的方法等等。姜哲[1]对声辐射模态作了深入研究，并利用声辐射模态对平板的辐射声场进行了重构。陶建成[2]以简支矩形板为研究对象，分别运用振动模态和声辐射模态对其辐射声功率进行了预报，并比较了两种模态展开方法对传感器数目的要求。Williams和Maynard[3]忽略声波的波长对结果分辨率的影响，提出了近场声全息技术。Lu和Wu[4]以一个无限大障板简支的薄板为研究对象，通过Helmholtz波动方程得到声压的球面波函数表达式，对简支薄板的辐射声场进行了预报，并与解析法所得到的结果进行了对比。童仲尧等[5]对三种主流的近场声全息技术的算法进行了分析和对比，综述了近场声全息发展的现状。George Chertock[6]从物理声学的角度，基于平面波假设直接建立表面声压与声速的简单联系，避免了Helmholtz积分方程及其逆矩阵的求解，实现了高频范围内辐射声场的快速预报。王斌[7]以声场叠加原理为基础，根据声传递特性直接建立结构表面振动与辐射声场间的传递关系提出了单元辐射叠加法，在更宽的频率范围内实现了结构辐射声场的快速近似评估。和卫平[8]从结构振动模态与声辐射模态的概念出发，研究了两端简支单层圆柱壳振动模态与声辐射模态的耦合关系。尹玉[9]研究了结构表面振动传感器的布放对估算精度的影响，在传感器均匀布放的前提下，研究了声压估计、声功率估计以及声压变化量估计中，估计精度、变化量估计准确度与传感器数目、场点位置、激励源位置的关系。

本文基于模态的方法，运用欠定分离法实现了双层加筋圆柱壳有限数目测点评估结构辐射声场的目的，并分别通过数值和试验测试验证了该评估方法的有效性。

1 声场欠定分离评估理论

通过结构表面M个测点的振速及结构前N阶截断模态求解模态参与因子，是基于振动模态叠加原理评估结构振动和辐射声场的基础。现有的相关研究中，为使方程有唯一解，一般在M≥N的情况下求解模态参与因子，导致在N的值较大时需要布置非常多的传感器。为解决评估精度与传感器数目之间的矛盾，本文充分利用模态参与因子向量自身的稀疏特性，运用欠定分离法实现了在M＜N的情况下对水下双层加筋圆柱壳辐射声场的准确评估。

1.1 水下弹性结构的描述

对于水下弹性结构的振动响应，由结构干模态叠加原理，结构振动位移响应向量在频域中的解可以表示为：

式中：φr表示真空中结构的第r阶振型，ηr表示结构的第r阶位移模态参与因子。将（1）式表示成矩阵的形式，为：

式中：［Φ ］为结构在真空中的固有模态矩阵，称为干模态，可以看成是结构在空气中的模态矩阵，［η］为位移模态参与因子向量。

因此对于水下双层加筋圆柱壳结构，若将其离散为n自由度系统，结构表面法向振动速度场可以表示为：

式中：［ξ］n×1为速度模态参与因子向量。

由模态叠加原理，高阶模态对结构振动响应的贡献很小，所以可以采用模态截断的方法，忽略高阶模态影响。设选取的模态阶数为N，（3）式可表示为：

从而可得结构表面任意M个测点法向振速为：

对于由（5）式确定的线性方程组，当M≥N时，（5）式为超定方程组，通过最小二乘法可以得到［ξ］N×1的唯一解，但此时测点数目必须大于或等于模态的数目。对于复杂的结构，当振动响应的频率较高时，需要的模态的数目较多，此时需要布置较多的传感器，实际中往往难以实现。

相比而言，M＜N时，测点个数可以小于模态截断数，更符合工程实际。此时（5）式为欠定方程组，方程的解非唯一，这也是在M＜N的情况下进行速度场评估的难点。由模态叠加原理，对于结构在某一频率下的响应，只有少数几阶模态的贡献较大，其它各阶模态对响应的贡献都很小，从而［ξ ］N×1向量具有一定的稀疏特性。本文的欠定分离评估方法正是从［ξ ］N×1向量自身的稀疏特性出发，从（5）式的所有解中，寻找最接近结构实际振动的解。

1.2 欠定方程组的求解

向量的稀疏性是指向量的大多数元素为零或接近零，而远大于零的元素的个数非常少，向量中远大于零的元素个数越少代表向量越稀疏。 （6）式所描述的是一个优化问题：当 ［V］M×1和 ［Φ ］M×N已知时，在M＜N的情况下，通过研究 ［ξ ］N×1满足的稀疏特性，对 ［ξ］N×1附加稀疏性约束，从等式条件的所有解中，找出满足［ξ］N×1向量稀疏特性的最优解，该最优解可以作为实际情况的近似解。

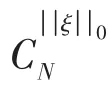
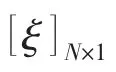
2 数值分析

2.1 数学模型

本文所选用的模型为工程领域常用的双层圆柱壳结构，具体结构形式如图1所示。其中，内壳直径850 mm，外壳直径1 050 mm，长1 050 mm，内壳厚4 mm，外壳厚2 mm，实肋板厚2 mm，内壳环肋截面尺寸：4 mm×33 mm；壳体材料：弹性模量 E=210 GPa，泊松比 m=0.3，密度：ρ=7 800 kgm-3。

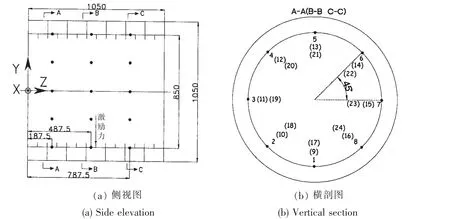
图1 双层加筋圆柱壳结构示意图（单位：mm）Fig.1 The schematic diagram of double ring-stiffened cylindrical shell(unit:mm)

2.2 基于壳体振速测试的声辐射评估

考虑水下双层加筋圆柱壳的测点一般布置在内壳，在双层加筋圆柱壳的内壳均布24个测点，测点由A到C截面依次编号为1～24号，如图1所示。以图中坐标系为参考坐标系，声场场点Q坐标（0，6 m，0.525 m）。以水下双层加筋圆柱壳的辐射声功率和场点Q的场点声压作为评估目标。

2.2.1 模态截断阶数的影响

根据上述评估方法，讨论评估中模态截断阶数对结果的影响。结果如图2所示。分析可以看出，在0～400 Hz的范围内，利用前300、500和700阶模态均可以较准确地评估出辐射声功率和场点声压，在400～800 Hz的范围内，利用前300阶模态评估出的辐射声功率结果偏差较大，利用前500和700阶模态评估出的辐射声功率和场点声压结果较准确。说明评估时所需要的模态截断阶数与结构振动响应的计算频率有关，计算频率越大，所需要的模态截断阶数也就越多，当截断模态包括了对响应贡献最大的几阶模态后，再增加截断模态的阶数对评估结果的影响不大，这与模态叠加法计算结构响应的原理是一致的。

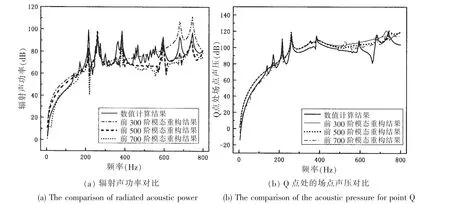
图2 24个均布测点不同模态截断阶数时的评估结果对比Fig.2 The comparison of reconstruction by twenty-four equispaced measure points with different mode number

2.2.2 测点布置方式的影响

分别选取两组测点，一组为图1中的24个均布测点，另一组为24个随机选取的测点，对比结果如图3所示。

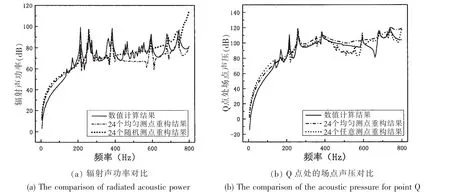
图3 24个均布测点和24个任意测点评估结果对比Fig.3 The comparison of reconstruction between twenty-four equispaced measure points and twenty-four arbitrary measure points

由图3可以看出，在0～400 Hz的频率范围内，通过24个均布测点评估所得的辐射声功率和场点声压结果与24个随机测点结果相差不大，在400～800 Hz的频率范围内，24个随机测点评估结果的扰动性较大，相比之下，24个均布测点评估出的结果更加稳定。这是因为均布测点的空间采样方式能够更全面地反映出结构的振动分布状态，可以得到更准确的评估结果，在布置测点时，建议优先选取均布的方式来布置测点。2.2.3测点数目的影响

所取测点数依次为12、24和40，其中12个测点为图1中1～24号测点中的奇数号点，24个测点为图1中1～24号测点，40个测点为在1～24号测点的基础上在每相邻两档测点的中间又对应均布8个测点所得到的测点。对比结果如图4所示。由图可看出，12个测点评估出的辐射声功率和场点声压偏差较大，24和40个场点评估出的辐射声功率和场点声压较准确。在400～800 Hz的频率范围内，40个测点比24个测点能够更准确地评估出场点声压。

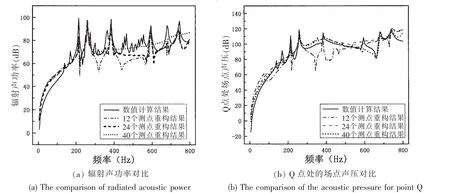
图4 不同数目均布测点评估结果对比Fig.4 The comparison of reconstruction by different equispaced measure points number

综合分析图2～4的结果可以看出，本文提出的欠定分离评估方法能够通过较少数目的测点对水下双层加筋圆柱壳辐射声场做出评估，并且该方法对测点数目的要求比较宽松，使得该评估方法在实际使用时有一定的灵活性。

3 试验验证

按图1结构形式和尺寸制作双层加筋圆柱壳试验模型，试验在水面开阔的清江水库进行，试验环境及测点布置如图5所示。试验中，在耐压壳上均布了24个传感器，测得了24个测点的振动加速度值，用以对结构的辐射声场进行评估，并通过水听器测得P点（0，4 m，0.525 m）和Q点（0，6 m，0.525 m）位置处的声压。按照图1（a）中的位置施加激励，与数值模拟采用单位激励力不同，试验时采用激振器进行激励。利用24个测点的振动测量值，对水下双层加筋圆柱壳的辐射声场进行评估，评估结果与试验测试结果对比如图6所示。

图5 试验环境及测点示意图Fig.5 The schematic diagram of experimental environment and measure points layout

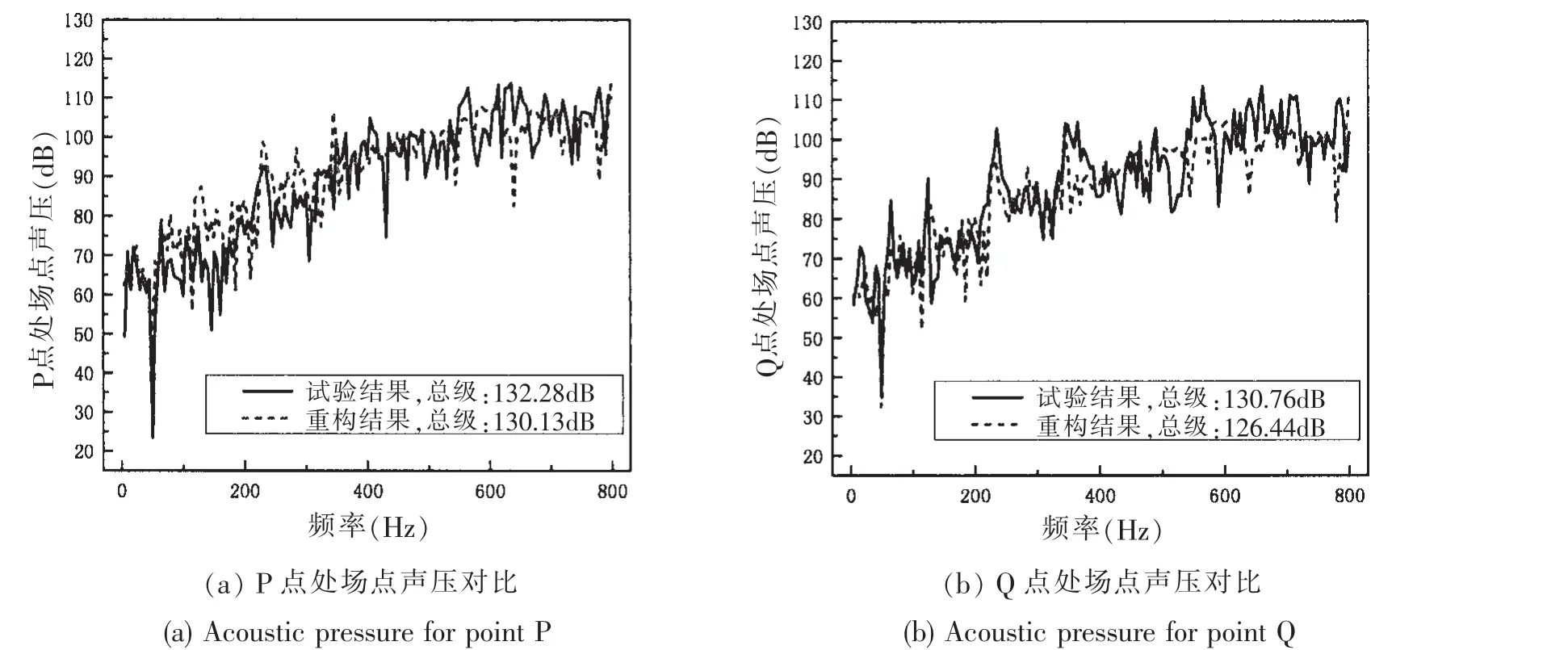
图6 试验测试结果和重构结果声压对比Fig.6 The comparison between experimental results and reconstructed results

从图6可以看出，在0～800 Hz的频率范围内，本文方法评估得到的场点声压结果和试验结果随频率变化的趋势基本是一致的。相比0～400 Hz频率范围的评估结果，在400～800 Hz的频率范围内，评估结果的误差有所增大，这与图4数值模拟的结果是一致的，此时增大测点数目可以进一步提高这一频段内场点声压评估结果的精度。在0～800 Hz的频率范围内，场点声压总级的误差在3 dB以内，满足工程要求。

4 结 语

针对基于结构振动的水下辐射声场评估问题，本文提出了一种欠定分离的评估方法，研究了模态截断阶数、采样测点的布置方式和测点数目对该方法评估精度的影响，并进行了试验验证。研究结果表明：

（1）在测点位置和数目一定时，当所取的模态阶数满足计算频率所需要的模态阶数后，再增加模态阶数对评估结果的影响非常小，这说明本文方法的评估结果在一定范围内不会随模态阶数的变化而出现振荡，具有较好的稳定性；

（2）在模态截断阶数和测点数目一定时，均布测点能够更好地反映出结构的振动分布状态，能够得到更稳定和精确的评估结果，在选取测点的位置时，建议优先采用均布测点的空间采样方式；

（3）在模态截断阶数以及测点布置方式一定时，增加测点数目可以采样得到更准确的振动分布，能够提高结构辐射声场评估结果的精度；

（4）数值结果及试验结果表明基于欠定分离方法的评估结果是可靠的，并且该方法中测点数目和选取的模态阶数相互独立，实现了较少数目振动测点评估结构辐射声场的目的，适用于工程中结构辐射声场评估问题。

[1]姜 哲.声辐射问题中的模态分析III声场重构[J].声学学报,2005,30(3):242-247.Jiang Zhe.A modal analysis for the acoustic radiation problems:III Reconstruction of acoustic fields[J].Chinese Journal of Acoustics,2005,30(3):242-247.

[2]陶建成,邱小军.两种模态展开法预测结构辐射声功率时振动传感器数目的要求研究[J].应用声学,2009,28(4):283-290.Tao Jiancheng,Qiu Xiaojun.Velocity sensor number requirements on using mode decomposition methods for structure borne sound power prediction[J].Applied Acoustics,2009,28(4):283-290.

[3]Williams E G,Maynard J D.Holographic imaging without the wavelength resolution limit[J].Physical Review Letters,1980,45(7):554-558.

[4]Lu H C,Wu S F.Reconstruction of vibroacoustic responses of a highly non-spherical structure using Helmholtz equation least-squares method[J].J Acoust.Soc.Am.,2009,125(3):1538-1548.

[5]童仲尧,洪伟荣,吴荣仁.近场声全息技术及其工程应用[J].振动与冲击,2008,27(S):302-304.Tong Zhongyao,Hong Weirong,Wu Rongren.Introduction of near-field acoustical holography and its application in engineering[J].Journal of Vibration and Shock,2008,27(S):302-304.

[6]Chertock G.Sound radiation from vibrating surfaces[J].J Acoust.Soc.Am.,1964,36(7):1305-1313.

[7]王 斌.基于表面振动监测的大型水下结构辐射噪声预报研究[D].上海:上海交通大学,2008:35-59.Wang Bin.Research on prediction of noise radiation by large underwater structure via surface vibration monitoring[D].Shanghai:School of Naval Architecture,Ocean and Civil Engineering Shanghai Jiao Tong University,2008:35-59.

[8]和卫平,陈美霞,魏建辉,张 聪.基于有限测点的单层圆柱壳辐射声功率计算[J].船舶力学,2012,16(10):1204-1211.He Weiping,Chen Meixia,Wei Jianhui,Zhang cong.Calculation of acoustic power radiated from a cylindrical shell based on a limited number of measurements[J].Journal of Ship Mechanics,2012,16(10):1204-1211.

[9]尹 玉,章林柯,陶建成.圆柱壳结构声辐射估计中的振动传感器数目要求[J].振动与冲击,2013,32(2):50-55,61.Yin Yü,Zhang Linke,Tao Jiancheng.Study of vibration sensors placing in the estimations of structure acoustic radiation[J].Journal of Vibration and Shock,2013,32(2):50-55,61.

[10]Mohimani H,Babaie-Zadeh M,Jutten C.A fast approach for overcomplete sparse decomposition based on smoothed l0norm[J].IEEE Transactions on Signal Processing,2009,57(1):289-301.

[11]Donoho D L.For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution[J].Communications on Pure and Applied Mathematics,2006,59(6):797-829.

[12]Li Y Q,Cichocki A,Amari S.Analysis of sparse representation and blind source separation[J].Neural Computation,2004,16(6):1193-1234.

[13]Bofill P,Zibulevsky M.Underdetermined blind source separation using sparse representations[J].Signal Processing,2001,81(11):2353-2362.

[14]Takigawa I,Kudo M,Toyama J.Performance analysis of minimum l1-norm solutions for underdetermined source separation[J].IEEE Transactions on Signal Processing,2004,52(3):582-591.

Research on prediction of radiated acoustic field for submerged double ring-stiffened cylindrical shell using underdetermined separation

GUAN Shan-shan1,WU Shu-you1,TAO Xiang-fan1,CHEN Mei-xia2,CAO Wei-wu1
(1.Wuhan Second Ship Design and Research Institute,Wuhan 430064,China;2.HuaZhong University of Science and Technology,Wuhan 430070,China)

The prediction of radiated acoustic pressure field for double ring-stiffened cylindrical shell under water is of great importance to noise monitoring and control.Based on the vibration modes of a double ring-stiffened cylindrical shell in vacuum,an underdetermined separation method which can realize prediction of radiated acoustic pressure field of the submerged double ring-stiffened cylindrical shell with a few measurement points is proposed.The validity of the prediction results are analyzed through numerical and experiments methods.It demonstrates that the prediction precision is reliable.And the number of measuring points needed is acceptable.Consequently,this method has much better applicability.

acoustic field prediction;underdetermined separation;submerged double ring-stiffened cylindrical shell;vibration measurement point

TB532

A

10.3969/j.issn.1007-7294.2017.10.015

1007-7294（2017）10-1309-08

2017-05-21

关珊珊（1982-），女，高级工程师，E-mail:saraguan@163.com；

吴书友（1982-），男，高级工程师，E-mail:wsy1982@mail.ustc.edu.cn。