高中数学学习中类比推理思想的应用论述
2017-11-02彭克臣
◆彭克臣
高中数学学习中类比推理思想的应用论述
◆彭克臣
所谓类比推理思想,就是根据两个目标,找出其在某种层面的类似之处,以类比手法推理疑难问题。这种思想运用在数学学习中,可以提升学生的数学思维与创造能力。本文首先简要介绍了类比推理思想的概念,然后结合实际例子,提出了高中数学学习中运用类比推理思想的具体方法。
高中数学;类比推理;作用;运用
一、类比推理思想的概念分析
现阶段的高中数学学习当中,类比推理思想属于一种十分有效的方法,同时其也是数学学习时必须要掌握的内容。类比推理主要是利用两个对象之间的共有性质,针对其余相似或相同的元素作出类比推理,使学生对新的数学知识产生更加深入的了解,并把头脑中已学到的信息有效应用到实际解题过程中,自主寻求解决数学问题的新途径。从数学角度分析,类比推理思想是拓展新领域、开创新学习分支的主要手段,并且也是学生在学习时不可替代的独特方法。在高中数学学习中,学生应当合理采用此类方法,最大限度地启发自身的智慧,引发自己的灵感,运用科学有效的推理解答种种数学难题。
二、高中数学学习中类比推理思想的应用方法
(一)在性质定理学习中的应用。学生在数学学习过程中,必然会接触到相关数学定理。当学生看见新的数学概念后,会对其内容、性质和定理产生兴趣。这时可以运用类比推理法,让自己进一步熟悉数学定理的内容。例如,学到“空间中的平面性质”时,学生可以针对“平面几何”与“立体几何”的相关性质定理展开类比推理。首先,在平面几何中,假设直线a平行于b,b平行于c,则a就平行于c。而从立体几何角度看,若平面α平行于β,β平行于γ,则α平行于γ。此外,在平面几何中,如果两条平行直线由第三条直线截断,那么其同位角是一致的。在立体几何中,如果两个平行平面和第三个平面交叉,那么其同位二面角是一致的。最后,在平面几何中,所有的三角形都存在一个外接圆、一个内切圆。在立体几何中,全部四面体都有一个外接球与一个内切球。通过对上述相似的性质定理进行类比,能让学生在平面几何的基础上更高效地学习立体几何。
(二)在概念学习中的应用。概念是数学知识的基础,也是学生在学习时要重点把握的知识点。在课堂上学习新的数学概念时,学生要尽量多接触一些新材料,利用类比推理思想,在自己的脑海中形成对新概念的印象。例如,学到“二面角”这一概念时,学生可以针对“角”与“二面角”这两种概念进行类比推理。先从其定义展开分析,角的含义是指从平面中的某一个点出发,形成两条射线或是半直线,从而构成“角”的图形。二面角的含义则是从空间内的某一条直线出发,形成两个半平面,从而构成“二面角。”再从其组成元素分析,角是由射线或半直线、点或顶点组成,二面角则是由半平面、线或棱组成。最后从二者的表示法分析,角可表示为∠AOB,二面角可表示为:二面角α-α-β。这两种概念非常相似。学生经由类比分析,可以更加容易地掌握这一新数学概念。
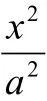
证明:设点M、P的坐标为(m,n)、(x,y),则N(-m,-n)
经过在解题过程中的实践运用,学生会更加容易地把握类比推理思想的运用方法。当学生学会利用该方法解答数学题目后,就能找到更为简便的解题方式,从而提高自己的学习信心。
结束语
在高中生的数学学习过程中,类比推理思想可以发挥出十分重要的效用。其能够将学生不熟悉的知识内容形象生动地呈现出来,易于学生理解和掌握。高中学生应注重在学习时妥善利用这一思想,并熟练运用该方法解决各种数学难题。
[1]刘波.类比推理在高中数学实践中的应用研究[J].现代交际,2014,05:142.
[2]尹海菊.类比推理在高中数学教学中的作用及应用方法[J].学周刊,2015,04:161.
(作者单位:长沙市明德中学)
