平稳随机过程激励下模糊随机梁的动力响应分析

王云飞, 马 娟, 陈建军

(西安电子科技大学机电工程学院， 陕西 西安 710071)

平稳随机过程激励下模糊随机梁的动力响应分析

王云飞, 马 娟, 陈建军

(西安电子科技大学机电工程学院， 陕西 西安 710071)

基于梁结构几何尺寸和物理参数客观存在的模糊随机性， 对时域上的结构位移响应的模糊随机相关函数矩阵以及频域上结构位移动力响应的模糊随机均方值分别进行理论推导， 再通过随机变量的矩法对结构应力响应模糊随机均方值的数字特征值进行推导. 最后通过一个12杆算例对所提理论的适用性进行了验证. 结果表明， 在对结构动力响应进行分析时， 其参数的不确定性的影响不能忽略.

二因子法； 模糊随机梁； 平稳随机激励； 模糊随机动力响应； 模糊数字特征值

0 引言

实际工程中， 除结构的几何尺寸和物理参数等具有不确定性外， 其所受的外激励也大多为不确定性的随机过程力. 目前对于在随机激励下的随机参数结构的动力学研究已有很多成果， 所用随机分析方法主要有： 蒙特卡洛数值模拟法[1]、 摄动法[2-3]、 基于正交展开理论方法[4-5]、 随机因子法[6-10]以及概率密度演化方法[11-13]. 其中， 蒙特卡洛法虽具有普遍性， 但因该方法往往需要大量计算， 且判断数据的收敛性时具有一定的困难. 摄动法存在的久期项问题使得其本身具有一定的逻辑缺陷. 采用正交展开方法的随机结构动力分析虽有不受参数变异量大小限制的优点， 但当考虑的随机变量较多或其变异系数较大时， 显著增加的正交展开多项式的项数将会导致工作量的激增. 随机因子法不仅具有计算量小的特点， 还能在对结构进行随机动力分析时较为清晰地反映结构的随机参数对结果的影响. 概率密度演化方法比上述以及其他只能反应结构数字特征的方法具有显著的优点， 其可以直接给出一般多自由度结构体系动力响应的即时概率密度函数.

与只考虑一种不确定性(模糊性或随机性)结构的动力响应分析相比， 模糊随机结构的随机振动分析则要困难和复杂得多. 迄今， 仅有少量关于模糊随机结构的研究成果发表[14-15]， 但主要采用摄动法， 该方法计算量大且无法考察结构模糊随机参数对动力分析结果的影响， 因此目前仅用于模糊随机结构静力分析和结构稳定性问题. 本研究通过二因子法， 针对第一类模糊随机变量[16]对模糊随机结构进行动力学特性分析， 并以此为基础完成了平稳随机激励下模糊随机梁的位移和应力响应均方值的模糊数字特征表达式的推导.

1 结构的平稳随机响应分析

对在平稳随机荷载激励下n自由度结构的有限元动力方程进行振型解耦及Duhamel积分后的形式解， 获得了结构节点位移响应的相关函数矩阵：

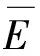
(1)

其中:u(t)、φ和h(t)分别表示为结构节点位移、 正则振型矩阵和结构脉冲响应函数矩阵，Rp(τ-τ1+ε)是荷载P(t)的相关函数矩阵.

对式(1)采用傅里叶变换即可求得位移响应功率谱密度函数矩阵Su(ω)：

其中:ω为随机荷载干扰频率；Sp(ω)、H(ω)和H*(ω)分别为荷载的功率谱密度函数矩阵、 结构频率响应函数矩阵以及H(ω)的共轭矩阵.

对式(2)在频域[0,ωc]上积分， 得到结构位移响应的均方值矩阵为：

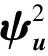
(3)

其中:ωc是响应计算所用的截止频率.

通过式(3)， 便可以获得在第m个自由度上结构的位移响应均方值：

其中:φm表示振型矩阵φ里的第m个行向量.

由此， 通过有限元理论中的单元节点位移与所施加应力之间的定量关系， 便可以类似地推导出e单元上应力响应f(e)(t)的均方值矩阵：

2 模糊随机结构在平稳随机激励下的动力响应分析

2.1 时域上模糊随机结构位移响应的模糊随机相关函数矩阵

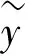
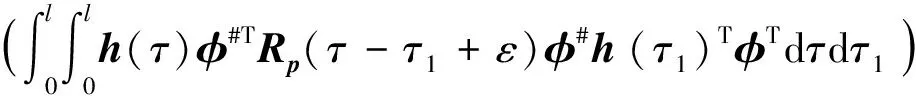
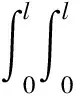
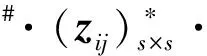
2.2 模糊随机结构位移和应力响应在频域上的模糊随机均方值

由此， 通过有限元理论中的单元节点位移与所施加应力之间的定量关系， 可导出任意单元应力响应模糊随机功率谱密度矩阵， 则对于结构中任一单元， 其应力响应的均方值模糊随机变量可表示为：

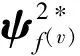
2.3 模糊随机结构动力响应均方值的模糊数字特征

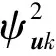
类似有:

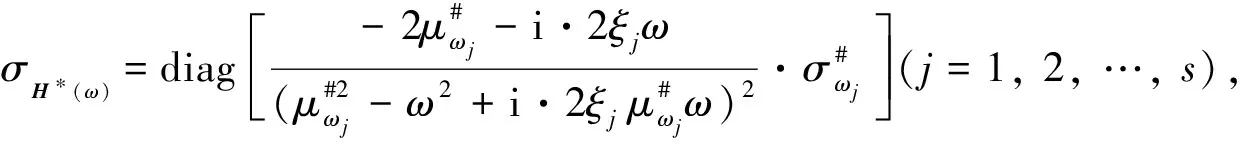
同理， 通过由代数综合法亦可求得结构上任一应力响应及其导数响应的均值和均方差：

类似有:

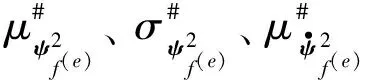
3 算例

设平面12杆刚架结构有限元模型的节点和单元编号如图1， 其为弹性模量E和质量密度ρ均为模糊随机变量的钢结构， 且取值为对称正态模糊数y=(y#,α,α)LR：E=(2.058×105kg·m-3, 0.04×103kg·m-3)LR. 以最小隶属度对各参数做λ水平截集， 各参数分别被转化为区间数ρ=[7.6×103kg·m-3, 8×103kg·m-3, 8×103kg·m-3],E=[195.8 GPa, 215.8 GPa]，E和ρ均服从正态概率分布. 取振型阻尼比ξj=ξ=0.01. 一个白噪声平稳随机过程力P(t)沿着X轴方向作用在节点9上， 它的自功率谱密度为S0=20N2·s-1, 而且它的中心频率ω0=45 Hz， 带宽B=90 Hz. 取截止频率ωc=ω0+(B/2)=90 Hz， 对结构的前16阶振型参振并计算.

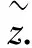
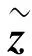
表1 12杆刚架结构取不同时间间隔ε时矩阵(zij)s×s的模糊因子

图1 平面12杆刚架结构 Fig.1 Plane 12-bar beam

表2 12杆模糊随机刚架结构用不同方法进行分析的结果比较

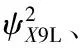
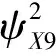
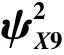
表3 位移响应均方值以及应力响应均方值的均值、 均方差

从计算结果可知：

1) 质量密度ρ对结构位移和应力响应均方值的模糊随机不确定性产生了较大的影响， 弹性模量E虽然也对该结构的模糊随机不确定性产生了影响， 但是影响程度却不如质量密度对其影响强度大.

2) 当仅考虑弹性模量E和质量密度ρ两者之一为随机模糊变量时， 结构在位移和应力上所表现出的响应均方值不确定性要比同时考虑两者均为随机模糊变量的情况下小. 除此之外， 当结构参数的模糊随机不确定性增大时， 会导致结构响应均方值的模糊随机不确定性增大.

4 结论

基于二因子法构建了平稳随机过程激励下模糊随机梁的动力响应分析模型并给出其求解方法. 对频域上的结构位移动力响应的模糊随机均方值， 时域上的结构位移响应的模糊随机相关函数矩阵分别进行了理论推导; 再通过随机变量的矩法对结构应力响应模糊随机均方值的数字特征值进行了推导; 最后通过一个12杆算例论证了结构的动力响应受其物理参数和几何尺寸的模糊随机性的影响， 从而对所提出的建模和求解方法的有效性可行性进行了佐证. 二因子法不仅适用于结构参数是模糊随机变量的情况， 当且仅当结构参数为随机变量或模糊变量时， 该方法也同样适用， 因而可以便捷地在工程中应用. 但是， 本研究仅研究第一类模糊随机问题， 而对于其他两类模糊随机问题(即： 清晰事件-模糊概率， 模糊事件-模糊概率)及其相应的动、 静力分析和可靠度研究将在后续研究中开展.

[1] HURTADO J E， BARBAT A H. Monte Carlo techniques for stochastic finite elements[J]. Archives of Computational Methods in Engineering, 1998, 5(1): 3.

[2] 王陶, 何欢, 闫伟, 等. 一种利用子结构综合技术的模型修正方法[J]. 振动与冲击, 2017, 36(2): 147-152.

[3] CHO K N. Mass perturbation influence method for dynamic analysis of offshore structures[J]. Structural Engineering and Mechanics, 2002, 13(4): 429-436.

[4] 周立明, 孟广伟, 李锋, 等. 基于随机场正交展开理论的Cell-based随机光滑有限元方法[J]. 东北大学学报(自然科学版), 2015, 36(8): 1 164-1 169.

[5] 张森文, 曹开彬 , 陈奎孚, 等. 精细积分时域平均法和扩阶系统法[J]. 力学学报, 2000, 32(2): 191-197.

[6] 靳红玲. 不确定性结构的动力学分析[D]. 西安： 西安电子科技大学, 2015.

[7] GAO W, CHEN J J, MA H B. Dynamic response analysis of closed loop control system for intelligent truss structures based on probability[J]. Structural Engineering and Mechanics, 2003, 15(2): 239-248.

[8] GAO W, CHEN J J, MA J,etal. Dynamic response analysis of stochastic frame structures under nonstationary random excitation[J]. Aiaa Journal, 2004, 42(9): 1 818-1 822.

[9] CHEN J J, CHE J W, SUN H A,etal. Probabilistic dynamic analysis of truss structures[J]. Structural Engineering and Mechanics， 2002, 13(2): 231-239.

[10] 高伟, 陈建军, 马洪波. 线性随机桁架结构的平稳随机响应分析[J]. 应用力学学报, 2004, 21(3): 92-95.

[11] LI J, CHEN J B. Probability density evolution method for dynamic response analysis of stochastic structures[J]. Journal of Vibration Engineering, 2004, 65(6): 882-903.

[12] 陈建兵, 李杰. 随机结构复合随机振动分析的概率密度演化方法[J]. 工程力学, 2004, 21(3): 90-95.

[13] 陈建兵, 李杰. 复合随机振动系统的动力可靠度分析[J]. 工程力学, 2005, 22(3): 52-57.

[14] 吕恩琳. 模糊随机有限元平衡方程的摄动解法[J]. 应用数学和力学, 1997, 18(7): 631-635.

[15] 尤芳, 陈建军, 马娟, 等. 随机-区间-模糊变量下的结构拓扑优化设计[J]. 机械设计与研究, 2016(4): 1-4.

[16] MA J, CHEN J J, XU Y L,etal. Dynamic characteristic analysis of fuzzy-stochastic truss structures based on fuzzy factor method and random factor method[J]. Applied Mathematics and Mechanics, 2006, 27(6): 823-832.

(责任编辑： 林晓)

Dynamicanalysisoffuzzy-randombeamunderstationarystochasticexcitation

WANG Yunfei， MA Juan， CHEN Jianjun

(School of Electro-mechanical Engineering， Xidian University, Xi’an, Shaanxi 710071， China)

The fuzzy-random correlation function matrix of structural displacement response in time domain as well as the fuzzy-random mean square values of structural dynamic response in frequency domain are derived in this paper with the structural physical parameters and geometric dimensions for the beam are fuzzy-random. So the fuzzy numerical characteristics of dynamic responses are then addressed based on the theory. The validity of the method presented is verified and illustrated via an engineering example, and results display that the uncertainty of structural parameters should not be neglected during the analysis of the structural dynamic response.

two-factor method; fuzzy-random beam; stationary stochastic excitation; fuzzy-random dynamic response; fuzzy numerical characteristics

O324 ； TP13

A

10.7631/issn.1000-2243.2017.04.0481

1000-2243(2017)04-0481-05

2017-3-30

马娟(1972-), 教授, 主要从事机械结构可靠性、 多场耦合结构的动力学等方面研究, juan.m@126.com

国家自然科学基金资助项目(11572233)； 国家自然科学青年基金资助项目(11102143)