斜拉索-磁流变阻尼器系统的频域自适应控制

陈昭晖， 陈宝春

(福州大学土木工程学院， 福建 福州 350116)

斜拉索-磁流变阻尼器系统的频域自适应控制

陈昭晖， 陈宝春

(福州大学土木工程学院， 福建 福州 350116)

基于频域LQG控制与Hilbert-Huang变换(HHT)， 并考虑磁流变(MR)阻尼器动力学， 提出斜拉索振动的频域自适应控制方法. 由HHT识别受控拉索的瞬时振动状态， 自适应调节控制器， 提高对目标特征频率的追踪能力， 且避免时域LQG控制需要对权参数进行试算选取的问题. 为验证所提出的自适应频域LQG(iAFLQG)控制算法的有效性， 通过与MR被动控制及时域LQG半主动控制相比较， 结果表明： iAFLQG控制能够更高效地利用MR阻尼器的动力特性达到最佳的拉索减振效果.

斜拉索; 磁流变阻尼器; 自适应控制; 非线性动力学; 随机激励

0 引言

索是斜拉桥上的关键结构构件之一. 由于其具有柔度大、 质量轻和结构阻尼小的特点， 极易遭受环境激励(如风雨激励等)的作用引起大幅度振动. 为抑制斜拉索振动， 在靠近索锚固端处安装阻尼器是常用的措施之一. 通常地， 被动阻尼器只能固定地对某一阶振动模态提供最优阻尼比； 且由于安装高度的限制， 被动阻尼器对超长斜拉索的减振效果不佳. 磁流变(MR)阻尼器因具有实时可调的阻尼特性以及能耗低、 可靠性好和稳定性强等优点， 在斜拉索半主动振动控制中已获得广泛研究和工程应用[1-6].

为充分发挥MR阻尼器的特性实现预期的控制效果， 很大程度上依赖于控制策略. 对于斜拉索， 线性二次高斯(LQG)控制是常用的算法[1, 3, 5]. 传统LQG控制是在时域上基于系统模型建立的方法， 通过最小化时域性能指标函数得到最优控制律. 带有状态估计器的LQG控制系统往往鲁棒性比较差， 若系统模型出现偏差或扰动， 闭环系统有可能出现不稳定. 其次， 柔性结构的振动不仅与外界激励强度还与其频率有关， 外激励一般难以预知或量测到， 但通过对结构响应的频域分析可反映出其特征频率成分， 由此在频域上对特征频率处重点衰减将是可行的. 为达到鲁棒的频域控制， 本文运用Gupta[7]提出的具有频域性能指标的频域整型LQG控制算法来设计半主动控制策略， 并引入Hilbert-Huang变换(HHT)[8]方法来达到自适应调节控制器增益的目标. 此外， 控制算法还考虑MR阻尼器的非线性动力特性以充分发挥其在不同电压下的耗能减振潜能. 最后， 对斜拉索振动控制进行了数值模拟实验以验证所提出的考虑MR阻尼器逆向动力学的自适应频域LQG(简称为iAFLQG)半主动控制算法的有效性， 并与MR被动控制和时域LQG半主动控制下的结果进行比较分析.

1 斜拉索-MR阻尼器动力学模型

1.1 斜拉索面内运动方程

图1 斜拉索示意图Fig.1 Configurations of an inclined cable

斜拉索示意如图1所示， MR阻尼器沿横向安装于靠近拉索的桥面锚固端处. 假设索的垂度较小， 其纵向运动较横向运动小得多可以忽略. 斜拉索的初始静力曲线可近似为抛物线[9]， 相对于其静平衡状态的横向运动微分方程可描述为:

式中：m为索的单位长度质量；c为面内阻尼系数；H1为索力沿x方向的分力；g为重力加速度；θ为索倾角；E为弹性模量；A为索横截面面积；L为索长；Le=L[1+(mgLcosθ/H1)2/8]；fey(x,t)为作用于索上的外激励力沿y方向的分力；fc(t)为控制力；δ()为Dirac Delta函数；xc为控制力作用于索上的位置.

式(1)是线性偏微分方程， 应用Galerkin法可得到其常微分形式， 并表达成状态空间方程为

1.2 MR阻尼器动力学模型

由于MR阻尼器的强非线性动力学特征， 其正向和逆向动力学采用基于试验数据的贝叶斯NARX神经网络建模方法[10]进行描述. 其中， MR阻尼器的正向动力学模型表示成：

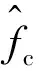
式中： Ninv(·)为映射逆向输入输出关系的贝叶斯NARX网络.

2 控制器设计

2.1 时域LQG控制

按照LQR控制理论， 式(2)的受控拉索系统的控制性能指标为：

或表示为：

式中：GKF为Kalman滤波器增益矩阵.

对于小阻尼斜拉索， 可认为其总机械能近似为弹性能和动能的总和. 由此， 令

则拉索的振动控制问题可通过耗散拉索系统的振动能量来实现. 另外， 控制权参数R需要通过反复计算比较确定， 以达到控制能量与控制性能的综合平衡.

2.2 频域自适应LQG控制2.2.1 控制律

根据Parseval定理， 式(6)可转化为频域上的广义控制性能指标[7]:

令

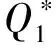
则性能指标式(11)改写成：

若传递函数Q1(jω)与R1(jω)均为正则的， 式(13)在状态空间可分别等效为：

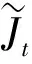
2.2.2 频域权函数设计

根据斜拉索风雨激振的现场实测， 发现索风雨振的主振动模态多为面内某阶低频固有模态； 对于特定拉索， 其振动频率会随着外界条件变化而转移[11]. 以减小斜拉索的主振动模态响应为控制目标， 针对第i阶振动模态的频域响应权函数可设计为:

其状态空间形式如式(15). 式(19)定义了中心频率为ωci、 带宽为β0和增益为γi的二阶带通滤波器， 它实现重点衰减以ωci(即拉索的主振动模态频率)为中心、 频宽为β0的窄带范围内的目标频率成分， 同时还可以减弱系统参数变化这类不确定性的影响而使控制具有鲁棒性.

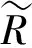
式中：ωr1与ωr2为滤波器的频率参数. 同样地， 式(20)可等效成式(16)的状态空间形式.

2.2.3 基于HHT自动加权

应用于斜拉索振动控制时， 基于索振动位移Yc信号， 利用HHT识别索的主振动模态频率ωi， 同时调节滤波器Q1(jω)的中心频率ωci为索的瞬时频率， 即ωci=ωi. 滤波器增益γi可根据第i阶IMF的瞬时能量Ei占所有IMF的总瞬时能量的比例进行自动调节， 即

可见，γi值表示第i阶模态对于拉索振动的参与程度.

2.3 半主动闭环控制律

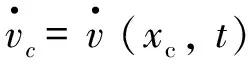
3 数值模拟分析

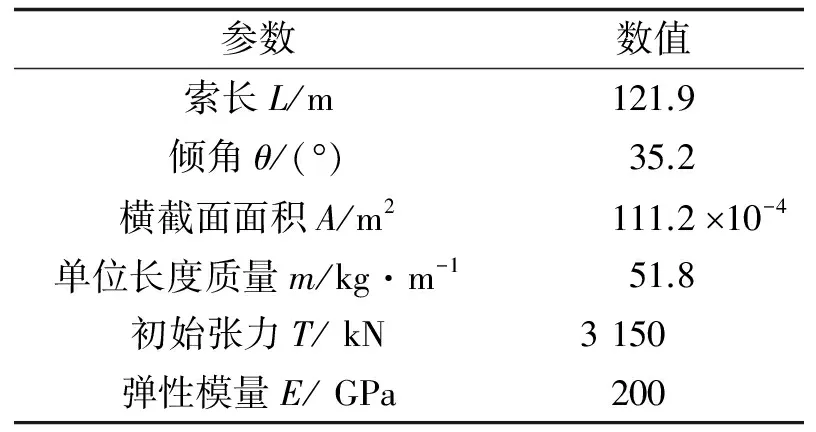
表1 斜拉索的主要参数

选取某大桥上一根斜拉索为分析对象， 验证所提出的iAFLQG控制策略的有效性， 并与MR被动控制、 时域LQG控制(iLQG)进行比较. 斜拉索的主要参数如表1所示， 其前5阶面内模态固有频率分别为1.07、 2.14、 3.20、 4.23和5.32 Hz， 相应的实测模态阻尼比为0.178%、 0.157%、 0.122%、 0.097%和0.108%.

采用随机激励模拟作用在斜拉索上的风雨激励， 使其发生以第3阶模态为主导的振动. 激励力取为频率范围0.5～5.0 Hz的带限白噪声. MR阻尼器安装于距拉索桥面端2.0%索长的位置处， 即xc/L=0.02； 距索桥面端1/6跨处的索位移用以评估控制效果. 外激励作用下， 无控制时索L/6处的位移峰值和均方根值分别为3.92 cm和1.26 cm.

首先， 分析被动工作模式下的MR阻尼器对拉索振动的控制性能， 控制结果如图2所示. 对MR阻尼器分别施加0.0～5.0 V恒定电压， 索L/6处的均方根位移和相比无控时的均方根位移减少量(即控制率)随施加电压值的变化如图2(a)所示. 可见， 索的响应随着电压水平的增加而减小； 当施加电压超过3.5 V， 图2(b)中的MR阻尼力趋于饱和(其均方根值约为780 N)， 使得控制效果减缓. 相比无控索的响应， 施加3.5～5.0 V电压时被动受控索的均方根位移降低了44%～46%.

图2 被动控制下的MR阻尼器对索振动的控制性能Fig.2 Control performance with passively operated MR damper

在时域iLQG控制下， 控制权重R的选取对控制效果的影响如图3所示. 由图3(a)可见， 随着区间[110-8, 110-6]内的R值的增大， 索的均方根位移降低. 当R小于110-8， MR阻尼力增加趋缓， 因此响应控制率变化不明显. 当R大于110-6， 因MR阻尼器的内在残余摩擦力的限制， 控制效果几乎不变. 当R=110-8， 索1/6跨的均方根位移减小到0.58 cm， 相比无控情况减小了53.6%； 相比最优MR被动控制(施加电压为5.0 V)， iLQG控制性能提高了13.6%， 所需MR阻尼力的均方根值为376 N， 仅约为最优被动控制力的一半， 如图3(b)所示.

图3 iLQG控制下的MR阻尼器对索振动的控制性能Fig.3 Control performance with iLQG controlled MR damper

运用频域iAFLQG控制策略， 权函数(19)和(20)将根据拉索系统的动力特性进行在线调节. 采用HHT识别主振动模态， 对滑动时间窗为5.12 s的反馈位移信号(采样周期t=0.01 s)进行EMD分解， 识别滤波器(19)的中心频率ωc， 增益γ则由瞬时能量按式(21)确定， 带宽β0设为0.5 Hz. 式(20)中，ωr1与ωr2分别取为0.5 Hz和第5阶模态频率5.32 Hz. 采用iAFLQG控制的结果见图4～7. 由图4(a)可见， HHT方法较准确地识别了索的主振动模态频率， 即第3阶模态频率3.20 Hz， 以调节Q1(jω)的中心频率ωc3. 图4(b)显示HHT识别的滤波器增益γ3集中在0.8～1.0之间， 说明拉索振动以第3阶模态占主导. 根据所识别的ωc3和γ3可实现权函数Q1(jω)和控制增益的自适应调节.

图4 HHT识别的权函数Q1(jω)的中心频率和增益Fig.4 Critical frequency and gain for weight Q1(jω) identified by HHT

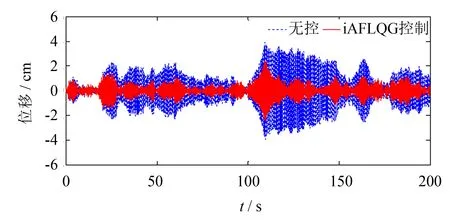
图5 拉索在无控和iAFLQG控制下的振动响应比较Fig.5 Comparison of cable responses without and with iAFLQG control

图5比较有控和无控索在L/6处的位移响应， 可见在iAFLQG控制下拉索的均方根位移相比无控时减小了60.7%. 同时， iAFLQG控制效果相比最优MR被动控制(5.0 V)和iLQG控制(R=110-8)分别提高了26.8%和15.2%. 图6显示了iAFLQG控制下， MR阻尼器逆向动力模型确定的控制电压在0～5.0 V之间连续变化， 达到全态控制. 预期和实际输出控制力比较见图7， 在此连续输入电压下， MR阻尼器的实际输出阻尼力准确地逼近预期的半主动控制力， 提高了控制效果.

图6 iAFLQG控制下MR阻尼器的输入电压时程Fig.6 Time history of voltage command with iAFLQG control

图7 预期和实际输出控制力比较Fig.7 Comparison between desired and applied control forces

4 结语

将频域LQG控制算法与HHT技术相结合， 并整合MR阻尼器的非线性动力特性， 提出斜拉索-MR阻尼器系统的频域自适应半主动控制算法(iAFLQG). 通过斜拉索在随机激励下的振动控制的数值模拟分析， 并与MR被动控制和传统时域LQG控制(iLQG)相比较， 结果表明： 1) iAFLQG和iLQG控制策略都能够仅以MR阻尼器安装位置处的索位移和MR阻尼力作为反馈信息实现斜拉索的半主动减振控制， 控制效果均优于被动控制； 2) 基于HHT的iAFLQG控制能够准确在线识别目标频率达到自动调节控制器增益， 并取得比最优MR被动控制和优化的iLQG控制更优越的控制效果； 3) 在控制策略中考虑MR阻尼器的非线性动力学， 能够改善MR阻尼器的实时阻尼力跟踪能力， 而获得更高效的控制性能.

[1] JOHNSON E A, CHRISTENSON R E, SPENCER B F Jr. Semiactive damping of cables with sag[J]. Computer-Aided Civil and Infrastructure Engineering, 2003, 18(2): 132-146.

[2] 陈政清. 斜拉索风雨振现场观测与振动控制[J]. 建筑科学与工程学报, 2005, 22(4): 5-10.

[3] DUAN Y F, NI Y Q, KO J M. State-derivative feedback control of cable vibration using semiactive magnetorheological dampers[J]. Computer-Aided Civil and Infrastructure Engineering, 2005, 20(6): 431-449.

[4] LI H, LIU M, LI J H,etal. Vibration control of stay cables of the Shandong Binzhou Yellow River Highway Bridge using magnetorheological fluid dampers[J]. Journal of Bridge Engineering, 2007, 12(4): 401-409.

[5] WEBER F, FELTRIN G, MOTAVALLI M. Measured linear-quadratic-Gaussian controlled damping[J]. Smart Materials and Structures, 2005, 14(6): 1 172-1 183.

[6] WEBER F, DISTL H. Amplitude and frequency independent cable damping of Sutong Bridge and Russky Bridge by magnetorheological dampers[J]. Structural Control and Health Monitoring, 2015, 22(2): 237-254.

[7] GUPTA N K. Frequency-shaped cost functionals: extension of linear-quadratic-Gaussian design methods[J]. Journal of Guidance and Control, 1980, 3(6): 529-535.

[8] HUANG N E, SHEN Z, LONG S R,etal. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995.

[9] IRVINE H M. Cable structures[M]. Cambridge: MIT Press, 1981.

[10] CHEN Z H, NI Y Q, OR S W. Characterization and modeling of a self-sensing MR damper under harmonic loading[J]. Smart Structures and Systems, 2015, 15(4): 1 103-1 120.

[11] NI Y Q, WANG X Y, CHEN Z Q,etal. Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(5): 303-328.

[12] BALAS M J. Feedback control of flexible systems[J]. IEEE Transactions on Automatic Control, 1978, 23(4): 673-679.

(责任编辑： 蒋培玉)

Adaptivefrequency-domaincontrolforstaycable-MRdampersystem

CHEN Zhaohui, CHEN Baochun

(College of Civil Engineering, Fuzhou University, Fuzhou， Fujian 350116, China)

An adaptive control solution to suppress cable vibrations is proposed by synthesizing a frequency-shaped linear quadratic Gaussian (LQG) control with the Hilbert-Huang transform (HHT) technique and considering the magnetorheological (MR) damper dynamics. Based on the transient structural state identified by HHT, adaptive tuning of controller is accomplished to enhance its frequency targeting capability, which also eschews theaprioritrial and error on the weight selection usually conducted in the time-domain LQG control. The proposed inverse dynamics based adaptive frequency-domain LQG (iAFLQG) control strategy is numerically verified in comparison with the passive MR damping and the time-domain LQG control, which demonstrates that the iAFLQG control exploits the intrinsic features of the MR damper in a more efficient way to substantially reduce the cable response.

stay cable; magnetorheological damper; adaptive control; nonlinear dynamics; random excitation

TB535

A

10.7631/issn.1000-2243.2017.04.0459

1000-2243(2017)04-0459-07

2017-02-22

陈昭晖(1982-)， 博士， 助理研究员， 主要从事结构振动控制、 智能材料及结构的研究， zhchen@fzu.edu.cn

国家自然科学基金资助项目(51608128)； 福建省自然科学基金资助项目(2016J05123); 福建省教育厅科技项目(JA15098)； 福州大学科技人才基金资助项目(XRC-1457)