基于UGNX的外啮合行星搅拌机运动特性研究
2017-11-01陈勇棠蒲明辉
陈勇棠,蒲明辉
(1.柳州职业技术学院 机电工程学院,广西 柳州 545006;2.广西大学 机械工程学院,南宁 530004)
[机械技术应用研究]
基于UGNX的外啮合行星搅拌机运动特性研究
陈勇棠1,蒲明辉2*
(1.柳州职业技术学院 机电工程学院,广西 柳州 545006;2.广西大学 机械工程学院,南宁 530004)
基于UGNX软件对某化工机械公司生产的某型号外啮合行星搅拌机运动部件进行运动仿真分析,掌握其运动特性,以便指导该型号搅拌机设计、生产及使用。
UGNX;行星搅拌机;仿真分析
行星搅拌机是双轴搅拌机中的一种,已有100多年的历史,主要用于物料的搅拌、混合和输送。由于利用行星结构传动,不仅低噪音,机械效率高,可节省动力使用,减少设备占用空间,而且因为搅拌器既绕着釜体中心公转,又绕着自身中心高速自转,在双重运动作用下,物料在釜体内的运动复杂,物料受到强烈的剪切和搓合,所以得到较好的搅拌效果,被广泛用于建筑、化工、医药、煤炭等行业。
本文针对某化工机械公司生产的某型号的行星搅拌机为研究对象,借助UGNX软件的运动仿真功能,全面、准确掌握该搅拌机运动部件的运动特性,从而更好地指导该搅拌机设计、生产及使用。
1 行星搅拌机的工作原理及运动特性要求
某化工机械公司生产的某型号的行星搅拌机主要结构如图1所示(去掉搅拌桶),包括:电机、减速器、横梁、行星箱、搅拌桨、床身等。

图1 行星搅拌机主要结构组成 (去掉搅拌桶)
其中传动装置结构如图2所示,太阳齿轮被固定,行星齿轮与行星箱是连接一体的,它们在主传动轴的带动下做公转,而行星齿轮与太阳齿轮是啮合的,故行星齿轮同时也在自传,从而带动搅拌轴既公转也在自传。行星齿轮传动简图如图3所示。
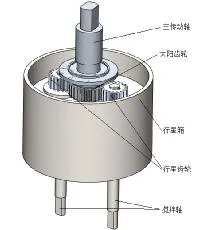
图2 传动装置结构图
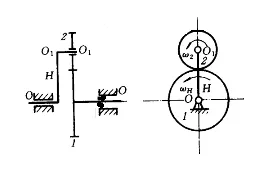
图3 行星齿轮传动简图
行星搅拌机工作的过程就是把机械能转化成物料的动能和热能的过程,主要依靠搅拌桨的旋转使得搅拌桶里的物料产生对流和涡流,使得物料各组分之间得以相互渗透、混合,逐渐达到均匀。因此,搅拌桨的运动轨迹不仅要覆盖搅拌桶的底面、不留“死区”,还应尽量多的交叉,从而让物料颗粒的运动轨迹尽量多地交叉,轨迹越复杂、拥有复杂轨迹的颗粒越多,混合的程度越高、越强烈,搅拌匀质性就越高,搅拌效果越好。
2 行星搅拌机的运动特性研究
2.1 行星搅拌机运动模型的建立
为了方便研究,把行星搅拌机的传动装置进行简化,如图4所示,所有运动件都在搅拌桶内,行星箱围绕回转中心O做公转,顺时针转动,角速度为ωH;两个行星轮上的搅拌桨既与行星箱同步公转,也分别围绕着各自的回转中心O1、O2自转,逆时针转动,角速度分别为ω1、ω2。搅拌桨上点的运动特性是最重要的,而两个搅拌桨又是对称分布的,因此只需研究一个搅拌桨上的点的运动特性即可。运动模型进一步简化后,并以搅拌桶中心为原点建立坐标系,即可得到搅拌桨上动点A的运动模型,如图5所示。搅拌桨回转中心O1到行星箱回转中心O的距离为R,动点A到搅拌桨回转中心O1的距离为r。为方便建立方程,假设 K=r/R,C=ω1/ωH,ωH=ω。
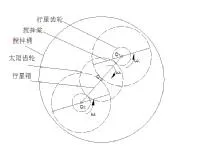
图4 行星搅拌机传动装置简图
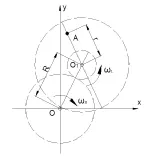
图5 搅拌桨动点运动模型
假设时间t=0时,搅拌桨与行星箱都位于竖直位置,并在同一直线上,经过时间t后,动点A顺时针转公转了ωHt的角度,同时逆时针自转了ω1t的角度,则运动参数方程为:
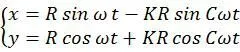
将式1-1对时间t求导,可得动点A的速度方程:
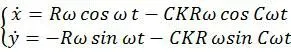
将式1-2对时间t求导,可得动点A的速度方程:
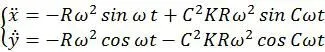
2.2 行星搅拌机的运动仿真
从动点A的运动方程可以知道当R和ωH固定时,K和C取值不同则动点A的运动特性不同。为了更直观地观察、对比,运动仿真时在搅拌桨的半边区域上取8个动点A1、A2、A3、A4、A5、A6、A7、A8,以及A2、A4、A6的对称点A'2、A'4、A'6作为示踪点,搅拌桨运动仿真简化模型如图6所示。
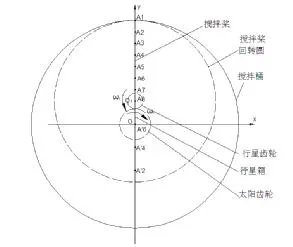
图6 行星搅拌机运动仿真模型
考虑实际生产中K的取值不可能太大,0<K<4即足够,动点A1、A2、A3、A4、A5、A6、A7、A8对应的K取值如表1所示。

表1 搅拌桨动点的系数K取值列表
运动仿真时取R=30mm,ωH=ω=60 r/min,即1 r/s,仿真时长为1s,分40步,则每个步长为0.025s。在UGNX软件中对仿真模型添加运动副约束、定义初始速度、转速方向、定义示踪点等设置后,分别按照C=0.5、C=1、C=1.5、C=2、C=2.5、C=3进行求解,得到动点的轨迹、位移曲线 (横坐标是时间,单位是秒;纵坐标是位移的幅值,即距离原点的距离,单位是毫米)、速度曲线、加速度曲线分别如图7、图8、图9、图10所示。
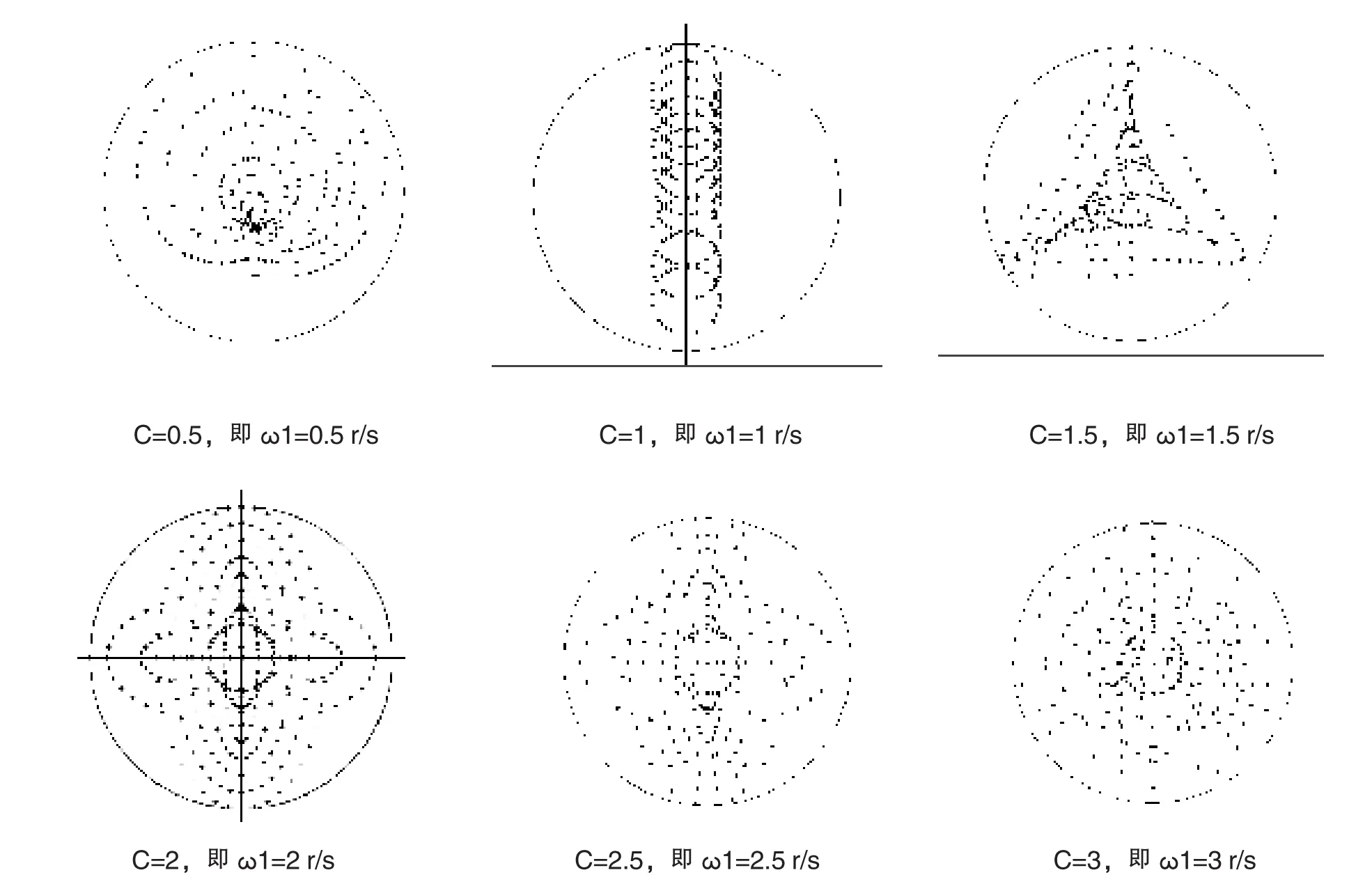
图7 不同C值时搅拌桨上示踪动点的运动轨迹
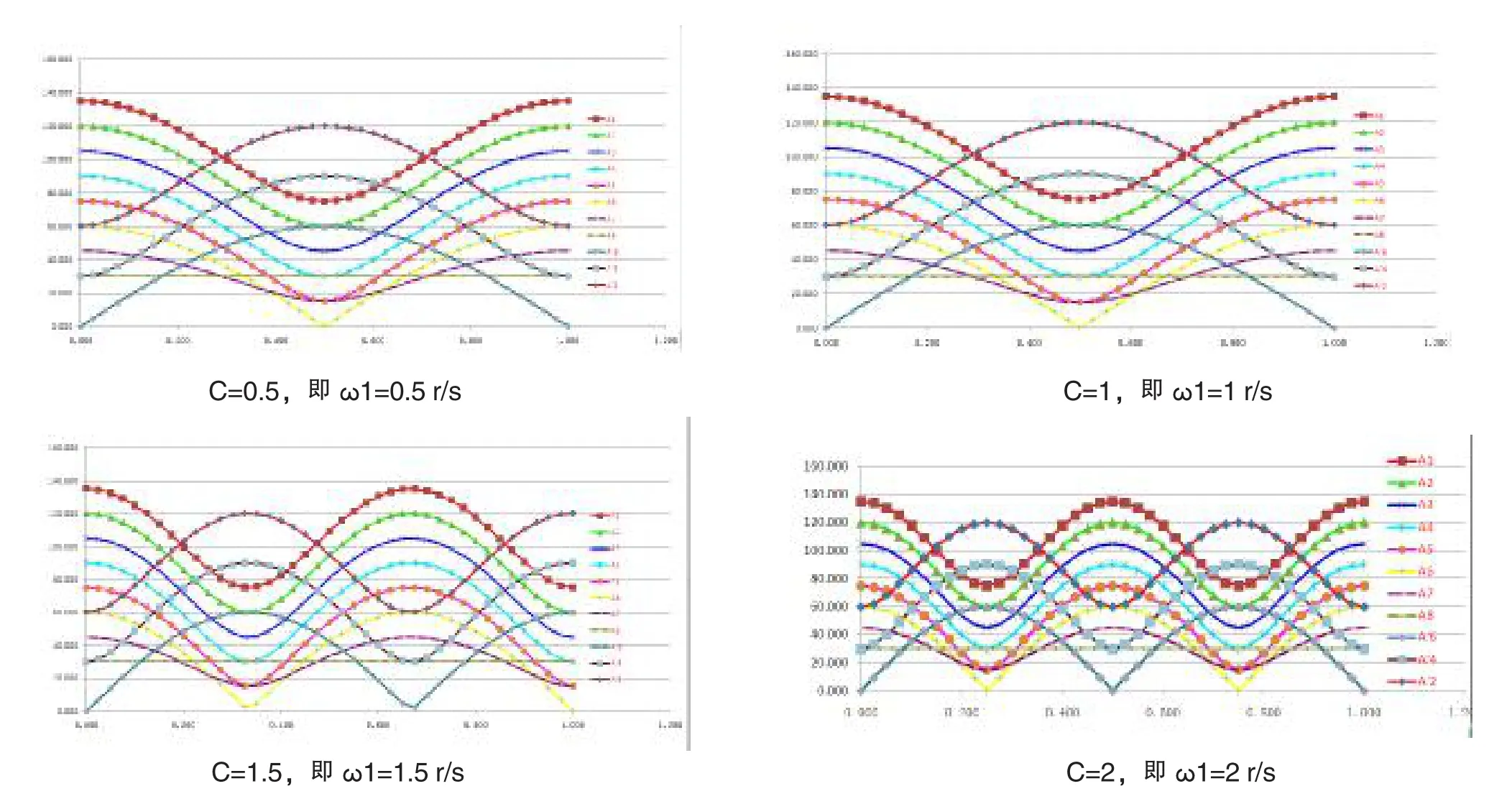

图8 不同C值时搅拌桨上示踪动点的位移曲线图
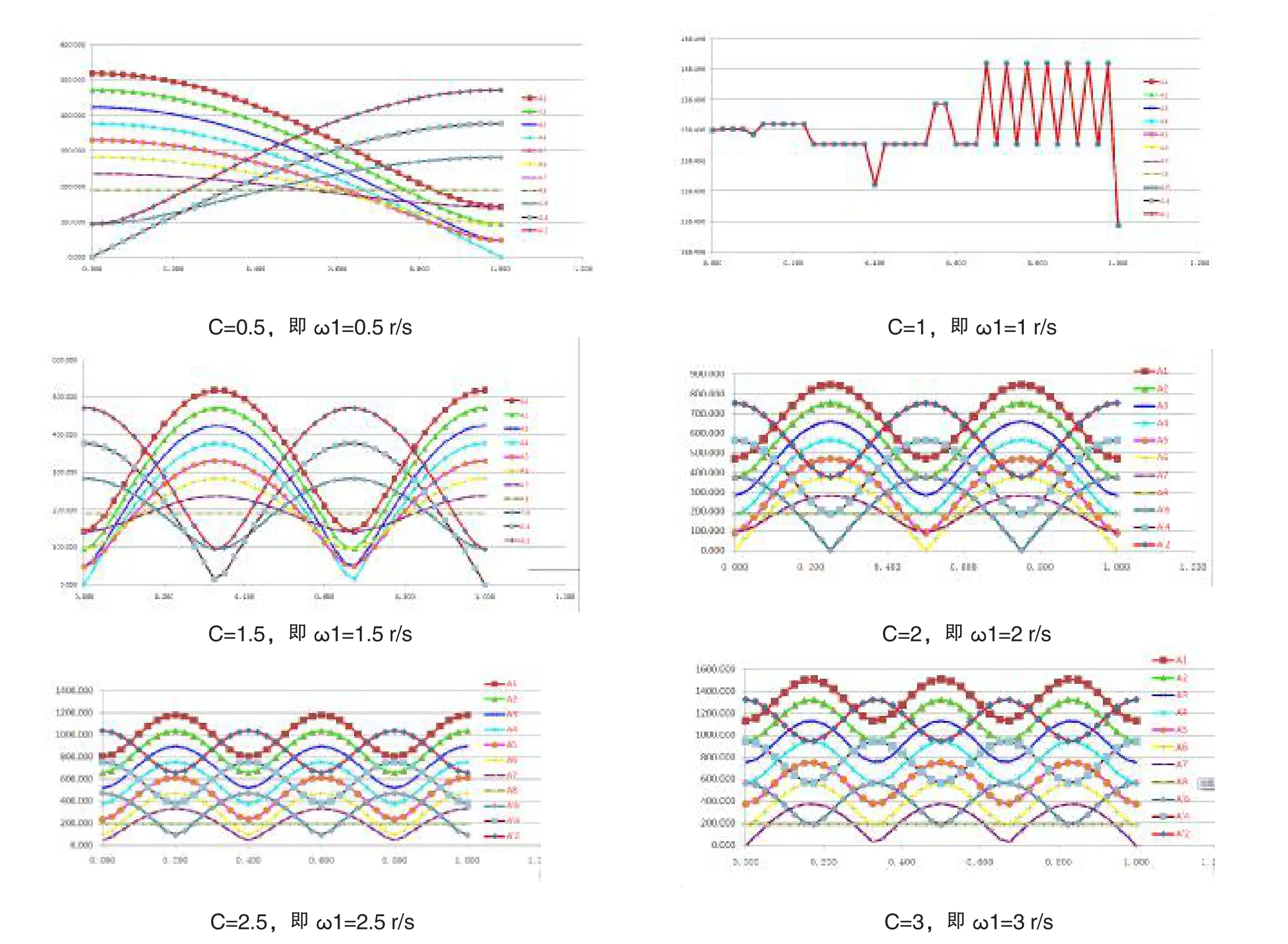
图9 不同C值时搅拌桨上示踪动点的速度曲线图
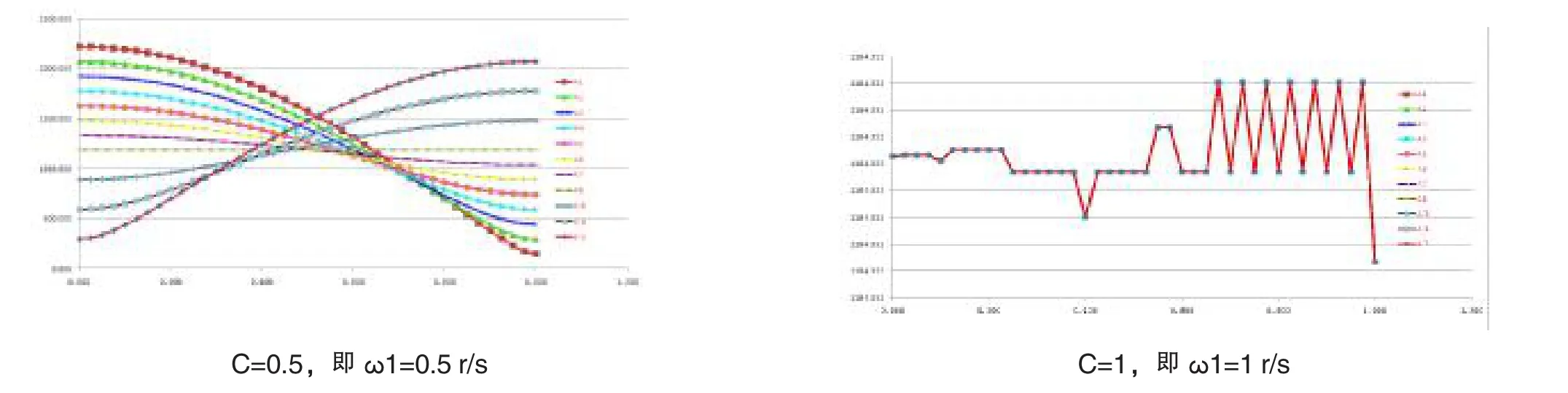
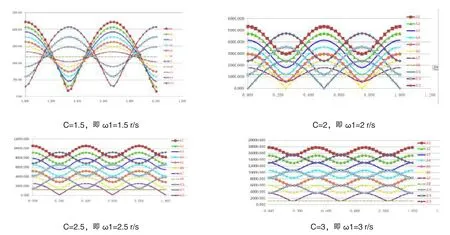
图10 不同C值时搅拌桨上示踪动点的加速度曲线图
2.3 行星搅拌机运动仿真结果分析
对仿真得到的图形分析得到以下主要的信息:
搅拌桶中心附近区域动点的轨迹密度比搅拌桶壁附近区域动点的轨迹密度大,同时即使仿真时搅拌桨与搅拌桶壁之间并无间隙,但靠近搅拌桶壁的区域总有一部分无动点轨迹,存在 “死区”现象,C值越小越明显。
不管C值为多少,动点A8的轨迹始终是绕着桶中心以半径为30mm做运动的圆周,位移幅值、速度幅值、加速度幅值都是恒定的。
C值越大,动点的轨迹密度越大,位移、速度、加速度曲线起伏变化的频率越大,而且速度和加速度的幅值变化幅度越大,说明搅拌的作用越大、越激烈。并且只有C值大于2以上,动点的轨迹才能覆盖搅拌桶的大部分区域,否则存在明显的搅拌 “死区”,搅拌料无法得到良好的搅拌。但同时也存在矛盾的另一面,即C值越大,速度和加速度幅值变化的幅度越大,越容易产生振动,对设备的破坏影响越大。
位于搅拌桨同一个半圆区域的动点轨迹外形是类似的,位移曲线、速度曲线、加速度曲线变化的趋势也是一样的,特别是C值越小于等于2时更明显,这样各向异性的动点数量就少,影响搅拌的均匀性和效率,影响搅拌效果。
动点A1~A8的速度从大到小,与动点到搅拌桨中心的距离成正比,离搅拌桶壁越近的物料获得的速度越大;当C值小于2时,远离搅拌桨中心的动点最大速度与最小速度差值越大,当C值大于等于2时,这种现象则消失。
3 结语
通过对行星搅拌机的运动部件进行仿真分析,可知行星轮的自转比公转越快,搅拌桨的搅拌路径越好,搅拌越激烈、效率越高,物料被搅拌得越均匀,并可以结合生产的实际条件进一步定量分析后得到太阳轮、行星轮较理想的齿数和尺寸。
[1]任春华,林朝阳,周国成.行星搅拌机的性能特点及其发展[J].泸天化科技,2011(1):54-62.
[2]朱霖龙,刘雅文,赵利军.长幅内旋轮线行星搅拌机研究[J].工程机械,2013(4):13-18.
[3]雷贤卿,侯少帅.双行星齿轮传动系统运动学分析与仿真[J].机械设计与制造,2014(11):68-70.
[4]祝文美.行星式砼搅拌机叶片运动轨迹分析[J].建筑机械化,1987(10):16-18.
[5]胡小康.UGNX4.0运动分析培训教程[M].北京:清华大学出版社,2006.
Abstract:Based on the UGNX software,this paper aims at the motion simulation analysis on the moving parts of a external gearing planet mixer produced by a chemical machinery company.As a result,it can fully and accurately gets the motion characteristics so as to give better advice about the design,production and usage of the planet mixer.
Key words:UGNX;Planet Mixer;Motion Simulation
Study on the Motion Characteristics of External Gearing Planet Mixer based on UGNX
CHEN Yong-tang1,PU Ming-hui2*
(1 College of Mechanical and Electrical Engineering,Liuzhou Vocational&Technical College,Liuzhou Guangxi 545006,China;2 College of Mechanical Engineering,Guangxi University,Nanning Guangxi 530004,China)
TH132.4
A
1671-1084(2017)04-0114-07
DOI 10.16221/j.cnki.issn1671-1084.2017.04.026
2017-02-08
陈勇棠,硕士,柳州职业技术学院机电工程学院讲师,研究方向为机械设计与制造及其自动化;*通讯作者,蒲明辉,广西大学机械工程学院教授、硕士生导师,研究方向为CAD/CAM及虚拟样机技术,E-mail:minghui@gxu.edu.cn。
