正则化参数求解方法研究
2017-11-01马建红
杨 浩,马建红
(河北工业大学 计算机科学与软件学院,天津 300401)
正则化参数求解方法研究
杨 浩,马建红
(河北工业大学 计算机科学与软件学院,天津 300401)
针对BP神经网络算法训练过程中出现的过拟合问题,提出了利用一阶原点矩,二阶原点矩,方差和极大似然估计概念的推广来计算L2正则化中正则化参数λ值的方法。该方法通过对算法数据集[X,Y]中的X矩阵进行运算得到的四个λ值,BP神经网络算法训练时通常采用的是贝叶斯正则化方法,贝叶斯正则化方法存在着对先验分布和数据分布依赖等问题,而利用上述概念的推广计算的参数代入L2正则化的方法简便没有应用条件限制;在BP神经网络手写数字识别的实验中,将该方法与贝叶斯正则化方法应用到实验中后的算法识别结果进行比较,正确率提高了1.14-1.50个百分点;因而计算得到的λ值应用到L2正则化方法与贝叶斯正则化方法相比更能使得BP神经网络算法的泛化能力强,证明了该算法的有效性。
BP神经网络;贝叶斯正则化;矩法估计;极大似然估计;方差;L2正则化
0 引言
机器学习中常常遇到高维小样本数据,高维小样本数据的变量空间维数很高,而样本空间维数并不高,因此往往会为建模带来一系列的问题,例如,训练样本数量的不足会导致过拟合问题,模型的泛化能力很差,极端情况下训练样本数小于变量数会导致建模过程需要求解病态的欠定方程组,进而导致模型的解不唯一,过拟合的时候,拟合函数的系数往往非常大,过拟合中拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大,而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
正则化方法可分为迭代正则化方法,直接正则化方法,L1和L2正则化方法与贝叶斯正则化方法。迭代方法如Landweber迭代法[1]和共轭梯度法(Conjugate Gradient,CG)[2],但是迭代方法中又引入了确定迭代次数等新的参数确定问题。直接正则化方法有截断奇异值(Singular Value Decomposition,TSVD)方法[3]与洁洪诺夫正则化(Tikhonov Regularization,TR)[4],洁洪诺夫正则化方法是在解决不适定问题中应用广泛的正则化方法,但由于这种方法具有饱和效应,不能使正则解与准确解的误差估计达到阶数最优,傅初黎[5]等对洁洪诺夫正则化方法进行了改进,提出了迭代的洁洪诺夫正则化方法,但未能使得其解决非线性算法的正则化参数问题,并且增加了迭代次数的确定问题。迭代正则化方法和直接正则化方法主要应用于线性问题的求解,并不能解决BP神经网络的非线性问题的正则化问题。
避免过拟合是BP神经网络算法设计中的一个核心任务。通常采用增大数据量,测试样本集的方法或者采用正则化的方法对算法性能进行提升。目前在BP神经网络算法正则化方面主要的解决办法是采用贝叶斯正则化方法(Bayesian Regularization,BR)和L2正则化方法。贝叶斯正则化由洁洪诺夫正则化方法发展而来的。在性能函数误差反馈的基础上,加上了权值的反馈以此提高算法的泛化能力,但贝叶斯正则化方法得到λ值的准确性存在依赖数据的分布和先验概率的问题[6-11]。L2正则化方法则需要确定它的正则化参数λ值,但目前尚未有有效的方法进行计算。
因此研究一种计算L2正则化中正则化参数λ值的方法是一件很有意义的一件事。本文通过应用统计中的矩法估计,方差和极大似然估计的概念推广的计算方法来得到正则化参数λ值,并应用到L2正则化方法中与采用贝叶斯正则化方法和人工选取得到的正则化参数确定正则化参数进行实验对比,人工选取正则化参数,如从λ=0.1,按照一定的步长增长如0.1,对比不同值得情况下,代价函数取得较小值时且假设函数未发生过拟合时的值,实验表明本论文中的方法得到的正则化参数值λ应用到L2正则化方法中相比于贝叶斯正则化方法更能够使得代价函数值小且假设函数不发生过拟合的现象。
1 解决原理
1.1 BP神经网络
BP神经网络[12-14]是基于前馈和反向传播算法的神经网络,包含输入层、隐含层和输出层,隐藏层节点数越多,隐藏层神经元数目越多,神经网络泛化能力越差,并且当遇到高维特征向量会给BP神经网络分类器带来过拟合的风险,影响BP神经网络在新的数据集上的识别率,也就是说BP神经网络的泛化表现不符合预期要求。
1.2 L2正则化
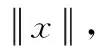
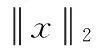
由L2范数而来的L2正则化方法,L2正则化就是在代价函数后面再加上一个正则化项:
(1)
C0代表原始的代价函数,后面一项是L2正则化项表示所有参数w平方的和,除以训练集的样本大小n。λ就是正则项参数,权衡正则项与C0项的比重,另外一个系数1/2,是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整。
L2正则化避免overfitting,推导如下:
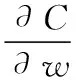
(2)
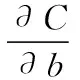
(3)
可以发现L2正则化项对b的更新没有影响,但是对于w的更新有影响:
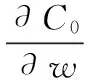
(4)
(5)
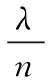
L2正则化项有让w“变小”的效果,更小的权值w,表示网络的复杂度更低,对数据的拟合更好即奥卡姆剃刀法则,而在实际应用中,也验证了这一点,L2正则化的效果往往好于未经正则化的效果。
1.3 BP神经网络与L2正则化
在BP神经网路的代价函数后面添加正则化项如下:
(1 -yk(i)log(1 - (hθ(x(i)))k)]+
(6)
1.4 矩法估计,方差,极大似然概念推广求解λ
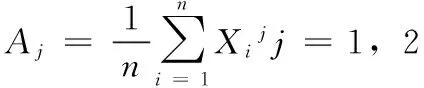
统计中的方差[15],是各个数据(X1X2...Xn)分别与其平均数之差的平方的和的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
极大似然估计[15],设总体X服从某类离散型分布,它的概率密度函数为P(x;θ),(X1,X2,...Xn)是取自总体的一个样本,在一次实验中获得样本值(X1,X2,...Xn)的概率为:
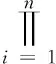
(7)
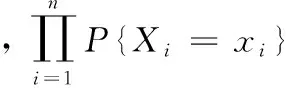
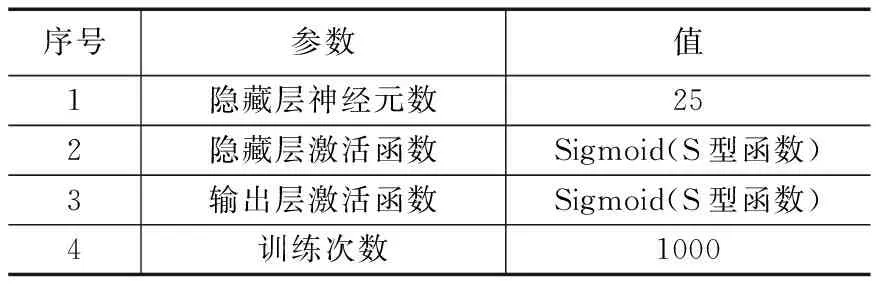
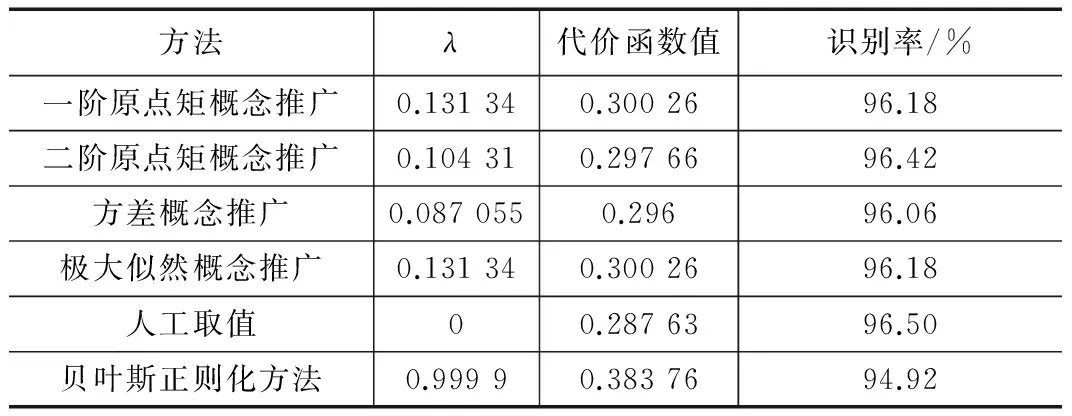
设(X1,X2,...Xn)是取自总体X~b(m,p)的样本,其中0 总体X的概率函数为: (8) 因此似然函数为: (9) (10) 解得p的估计值: (11) 以上是矩法估计、方差和极大似然估计的概念介绍,下面是对矩法估计、方差和极大似然概念的推广过程。 矩法估计、极大似然估计和方差在向量形式数据上的应用举例。假设判断一个灯泡质量的优劣,当灯泡寿命在4 500小时以上时,我们判断灯泡质量是优,灯泡寿命在4 500小时以下,判断是劣,总共测试n=5 000个灯泡,如第一个灯泡寿命x1=4 600,第二个灯泡寿命x2=1 800等,根据每个灯泡的寿命xi得到每个灯泡对应的评价,x1为优,x2为劣等,因而得到5 000个灯泡寿命数据及优劣评价,同时得到的是一维的1行5 000列的灯泡寿命数据的向量(x1x2...xn),n=5 000。此时灯泡寿命数据组成的向量用于矩法估计时,计算一阶原点矩公式如下: (12) 计算二阶原点矩公式如下: (13) 在计算极大似然估计时,用这个向量数据计算灯泡寿命的平均值除以灯泡个数得到极大似然估计值,计算公式如下: (14) 通过计算灯泡的平均寿命,算出每个灯泡与灯泡平均寿命值差值的平方,从而得到一组新的1行5 000列的向量(x1x2...xn),新的向量中的数据累加之后除以总数n就会得到方差,计算公式如下: (15) 目前,矩法估计、极大似然估计和方差都是对向量形式的数据的计算,样本数据Xi,1 (16) 二阶原点矩概念的推广,对算法数据集[X,Y]的Xmn矩阵每个xij数值的平方数值全部累加并且除以它的个数和m*n。时间复杂度为O(m*n),计算公式如下: (17) 方差概念的推广,对算法数据集[X,Y]的Xmn矩阵每个xij减去xij数值累加并除以矩阵数值个数m*n的平均值之后的平方进行累加,除以维数m*n。时间复杂度为O(m*n),计算公式如下: (18) 极大似然估计概念的推广,对算法数据集[X,Y]的Xmn矩阵的xij数值累加,并且除以维数m*n。时间复杂度为O(m*n),计算公式如下: (19) 例如在一个BP神经网络算法数据集[X,Y]中,X是5 000*400的矩阵,Y是5 000*1的列向量,则上述式子(16)(17)(18)(19)中n=5 000,m=400。 本文BP神经网络手写数字识别实验研究所使用的数据集来自在线课程coursera中吴恩达的机器学习课程的课后算法编程中提供的数据。 数据集中有5 000个训练实例,每个训练实例是20像素*20像素的灰度图像的数字。通过20*20的像素网格“打开”一个400维的向量。这5 000个训练的例子中的每一个数字成为一个行向量组成的5 000×400数据矩阵X。 图1 100个手写数字训练图像 Octave设计实现一个包含两个隐藏层的BP神经网络,网络参数选择如表1所示。 表1 实验中的神经网络结构 本文实验中,BP神经网络输入端是5 000*400的矩阵,λ是从-1开始以步长0.1增长至2。其中当λ=0时,代价函数较小为0.287 63,实验中测试集的手写数字识别率达到了96.5%,泛化表现不错。 通过对数据集5 000*400矩阵按照上述原理中的计算方法进行四个数值的运算,利用推广的一阶原点矩概念计算的结果是0.131 34,代价函数值是0.300 26,利用推广的二阶原点矩概念计算结果是0.104 31,代价函数是0.297 66,利用推广的方差概念得到的λ值是0.087 055,代价函数值是0.296 00,利用推广的极大似然估计概念得到的值是0.131 34,代价函数是0.300 26。将一阶原点矩0.131 34作为λ的值,经过训练之后,在实验中的测试集上手写数字识别率达到了96.18%,将二阶原点矩0.104 01作为λ的值,经过训练之后在测试集上识别率达到了96.42%,将方差0.087 055作为λ的值,经过训练之后,在测试集上识别率达到了96.06%,将极大似然估计得到的0.087 055作为λ的值,经过训练之后,在测试集上识别率达到了96.18%。由数据集[X,Y]中的X进行矩法估计中一阶矩估计、二阶矩估计、方差及极大似然估计概念推广的公式简单计算就可以得到λ值,并且算法有着不错的泛化表现。 为进一步验证所提方法的有效性,和贝叶斯正则化进行了比较。由贝叶斯正则化方法计算得到正则化参数值0.999 9作为λ的值,代价函数值是0.383 76,经过训练之后,算法识别率达到了94.92%,低于由矩法估计,方差和极大似然估计概念推广得到的λ值训练之后手写数字识别率的最低值96.06%,即下表2所示。 表2 试验中对比数据 实验证明,本文对一阶原点矩、二阶原点矩、方差及极大似然估计的概念推广计算得到的λ值,并用这4个值作为λ取值计算得到的代价函数值与人工多次选取找到的最优λ值得到的代价函数值极为接近,泛化表现也很接近。本论文的方法计算得到的λ应用到L2正则化方法进行算法的训练得到的手写数字识别率高于采用贝叶斯正则化方法的算法识别率。 由一阶矩估计,二阶矩估计,方差和极大似然估计概念的推广公式对数据集[X,Y]中的X矩阵计算得到的λ值,与人工多次选择正则化参数相比较效率更高,并且在算法训练之前就可以计算出正则化参数,很好地解决了算法有可能会出现的过拟合问题,减少了因为选取正则化参数而导致多次计算代价函数等导致的多余的运算量。 对比在BP神经网络算法上应用广泛的贝叶斯正则化方法,本文提出的正则化参数λ计算方法简单,没有条件假设限制,适用BP神经网络,并且实验证明本文中的方法比贝叶斯正则化算法得到的λ值更能有效减少过拟合,提高算法的泛化表现。 进一步的研究应该探讨本文方法应用于深度学习网络、线性回归及svm等算法中的可行性。 [1] 谢正超,王 飞,严建华,等.炉膛三维温度场重建中Tikhonov正则化和截断奇异值分解算法比较[J].物理学报,2015,64(24):17-24. [2] 崔 岩,王彦飞.基于初至波走时层析成像的Tikhonov正则化与梯度优化算法[J].地球物理学报,2015,58(4):1367-1377. [3] 王 旭,王静文,王柯元.阈值Landweber在MIT图像重建中的应用[J].东北大学学报(自然科学版),2016,37(4):476-480. [4] 雷 旎,刘 峰,曾喆昭.基于共轭梯度法的FIR数字滤波器优化设计[J].计算机仿真,2014,31(12):179-182. [5] 傅初黎,李洪芳,熊向团.不适定问题的迭代Tikhonov正则化方法[J].计算数学,2006. [6] 张刚刚.基于Tikhonov正则化的模糊系统辨识[D].辽宁科技大学,2014. [7] 高鹏毅.BP神经网络分类器优化技术研究[D].武汉:华中科技大学,2012. [8] 刘子翔.基于GA和LM算法优化的BP神经网络在域市空气质量预測中的应用研究[D].济南:山东大学,2015. [9] 赵 攀,陈 恳,汪一聪.基基于图像参数的BP网络之岩石颗粒体积估算[J].计算机测量与控制,2009,17(3):571-575. [10] 郑德祥,赖晓燕,廖晓丽.基于贝叶斯正则化BP神经网络的森林资源资产批量评估研究[J].福建林学院学报,2013,33(2):132-136. [11] 刘 源,庞宝君.基于贝叶斯正则化BP神经网络的铝平板超高速撞击损伤模式识别[J].振动与冲击,2016,35(12):22-27. [12] 宋 雷,黄 腾,方 剑,等.基于贝叶斯正则化BP神经网络的GPS高程转换[J].西南交通大学学报,2008,43(6):724-728. [13] Zhang S H,Ou J P.BP-PSO-based intelligent case retrieval method for high-rise structural form selection[J].Science China Technological Sciences,2013,56(4):940-944. [14] Rakhshkhorshid M ,Teimouri S S A .Bayesian regularization neural networks for prediction of Austenite formation Temperature(Ac1 and Ac3)[J].ScienceDirect.2014,21(2):246-251. [15]刘达民,程 岩.应用统计[M].北京:化学工业出版社,2005. Research on Method of Regularization Parameter Solution Yang Hao, Ma Jianhong (Hebei University of Technology,School of Computer Science and Engineering,Tianjin 300401,China) Aiming at the over fitting problem of BP neural network algorithm, this method is put forward to calculate the value of the regularization parameter applied to L2 regularization by using the concept of the first order origin moment, the two order origin moment, the variance and the maximum likelihood estimation.This method based on theXmatrix of data sets to compute four value.Compared with the Bayesian regularization method used to train the BP neural network, Bayesian regularization method is depend on the prior distribution and the distribution of data dependence. The calculation method in this paper is simple and has no application conditions. In BP Neural Network handwritten digit recognition experiments, this method compared with the Bayesian regularization method improve the correct rate about 1.14-1.50 percentage points. Therefore, the method in this paper makes the algorithm more efficient.This method is validity. BPneural network;regularization;maximum likelihood Estimation ;variance;moment estimation ;L2 regularization 2017-02-24; 2017-03-15。 杨 浩(1994-),男,河北石家庄人,硕士研究生,主要从事数据挖掘方向的研究。马建红(1965-),女,河北保定人,教授,博士生导师,主要从事计算机辅助创新设计过程与方法、TRIZ、软件工程及数据挖掘等方向的研究。 1671-4598(2017)08-0226-04 10.16526/j.cnki.11-4762/tp.2017.08.058 TP301.6 A
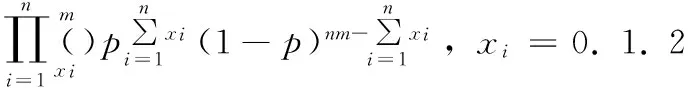
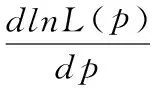
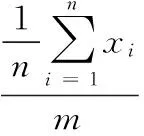
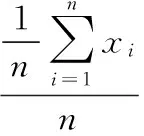
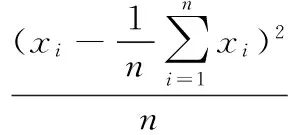
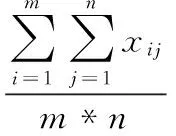
2 分析与讨论
2.1 数据采集与处理
2.2 神经网络结构
2.3 实验结果分析
3 结论
