振动对光纤陀螺线形测量系统影响分析

张 震,杨 燕,郑 磊,杨丹丹,甘维兵,胡文彬

(1.武汉理工大学 信息工程学院,武汉 430070； 2.武汉理工大学 光纤传感技术国家工程实验室, 武汉 430070；3.武汉理工大学 光纤传感与信号处理教育部重点实验室, 武汉 430070)

振动对光纤陀螺线形测量系统影响分析

张 震1,3,杨 燕2,郑 磊2,杨丹丹2,甘维兵3,胡文彬2

(1.武汉理工大学 信息工程学院,武汉 430070； 2.武汉理工大学 光纤传感技术国家工程实验室, 武汉 430070；3.武汉理工大学 光纤传感与信号处理教育部重点实验室, 武汉 430070)

在使用光纤陀螺测量系统对桥梁线形进行测量的过程中，由于线形测量结果是通过积分算法得到的，所以来自汽车发动机和路面不平的振动影响会给测量结果带来巨大的误差，并且这类误差会随着测量时间和距离的增加变得越来越大，呈现出发散的特性;为了减小这些振动给测量结果带来的误差，可以使用时频分析的手段，通过时间信息和运动速度得到位置和路况信息，进而得到不同路况下的频域特点;选择路面完好的路段进行实验，点状减速带代表路面不平，使用Morlet小波对光纤陀螺采集到的信号进行时频分析，发现了不同工况下带来的振动噪声信号的频域特点，并且确定了27 Hz以上均为振动带来的噪声信号;在实际对某跨江大桥的线形测量中，使用切比雪夫滤波器去除光纤陀螺所采集到27 Hz以上的噪声信号，相比没有使用低通滤波处理的线形，测量精度提高了50%。

光纤陀螺；线形测量；信号处理；振动；Morlet小波；切比雪夫滤波器

0 引言

桥梁结构的线形可以反演出结构内力的变化[1]，不但直观而且易于处理，是评估桥梁安全的重要指标之一。目前，桥梁结构线形测量的常用方法是使用水准仪或全站仪等工程测量仪器测量桥梁的多个离散点的高程，然后再通过拟合测量数据[2]以实现对桥梁结构的线形测量。然而这类采用人工观测的“点式”测量方法，不但测量效率非常低、测量周期非常长，更是难以准确捕捉到挠度形变的具体位置，尤其是位于未布点的潜在病害，常常会因为被拟合的线形所淹没，进而带来较大的安全隐患，现有的测量手段难以满足对桥梁结构线形检测的要求。

以光纤陀螺为核心的光纤陀螺线形测量系统可以实时采集以汽车为运载体的运动参数信息，然后根据采集到的运动参数信息进行积分计算，就可以得到运载体的运动轨迹曲线，进而可以实现快速连续地测量桥梁结构线形，以解决目前桥梁结构线形常用测量方法的局限性[3]。然而，正是因为光纤陀螺线形测量系统是通过积分算法实现的，所以在测量过程中，车辆发动机[4]的振动和路面不平整所带来的误差会随着测量时间和距离的增加，逐步累积，越来越大，呈现出发散特性，最终，会给测量精度带来巨大的负面影响。

本文使用数字信号处理的手段，从频域的角度分析出有效信号和噪声信号的频谱差异，为使用其他辅助手段提高测量精度提供了理论依据，并去除了部分噪声信号，有效的提高测量精度。

1 桥梁结构线形测量技术的工作原理

光纤陀螺所采集的是运载体运行轨迹的角速度数据，通过对实时变化的角速度数据进行积分运算，就能获得桥梁连续线型轨迹的角度变化，再联合各步积分间距的距离变化量，就可以实现桥梁结构线型的连续轨迹的输出，如图1。假设运载体运动轨迹上任意一点点的坐标为(Xi，Yi)，该点的线速度，角速度和初始角分别用υi、ωi、θi表示，则当运行的位移极限小时，则第i+1点的坐标(Xi+1，Yi+1)为：

(1)

(2)

(3)

根据(1)～(3)建立的递推关系就可以展开桥梁连续线型轨迹的计算：

图1 光纤陀螺线形测量理论原理示意图

由此可知，线形测量系统的测量结果是通过积分算法得到的，因此源自于汽车自身和路面不平所带来的振动噪声信号会带来测量误差，而且该误差会随着测量时间和距离的增加而变得越来越大，并且呈现出发散的特性。因此，光纤陀螺桥梁结构线形测量过程中，桥面的不平整和由汽车自身引起的振动是不可忽视的重要误差来源，会对整个测量结果产生较大的影响。

2 复Morlet小波变换基本原理

传统的傅立叶变换只能获取一段信号总体上包含哪些频率成分，但是不能获知各成分出现的时刻，在实际的应用中有很大的局限性。然而，实际的道路中有多种不同的路况，要分析不同路况下陀螺采集数据的频域特点，则需要使用时频分析的手段进行时频分析，通过时间信息和运动速度得到位置和路况信息，进而得到不同路况下的频域特点。这里选择使用复Morlet小波时频分析，可以分析各成分出现的时刻，适用于真实路况下陀螺数据的分析。

2.1 小波变换

假设信号x(t)为平方可积函数，即x(t)∈L2(R),φ(t)为基本函数或母小波函数，则式(4)称为信号x(t)的小波变换:

(4)

式中，*代表复数共轭；a>0是尺度因子；为时间平移尺度，任意的小波函数φ(t)必须满足式(5):

(5)

上述的小波变换可以在频域内表示为:

(6)

因此，信号x(t)的小波变换可以通过式(7)进行计算：

(7)

式中，F-1表示Fourier逆变换。

复Morlet小波的数学表达式为：

(8)

式中，fb为小波带宽；fc为小波中心频率。小波中心频率fc决定了波形的振荡频率，小波带宽参数fb决定了波形振荡的快慢程度。

2.2 切比雪夫滤波器

为了去除线形测量设备采集到的噪声信号，可以使用数字信号处理的方式对线形测量的输出设备进行处理，提高测量精度。切比雪夫滤波器是线代信号处理中的经典滤波器。其特点是：误差值在规定的频段上等波纹的变化。

切比雪夫滤波器的振幅平方数为：

式中，Ωc为有效通带截止频率；ε为与通带波纹有关的参量；VN(x)为N阶切比雪夫多项式。

3 实验设计

3.1 实验设备平台

光纤陀螺线形测量系统如图2所示，由载体汽车，光纤陀螺，内置存储设备及电源与线速度传感器组成。

图2 实验装置示意图

其中，光纤陀螺用于采集载体汽车的角速度数据，线速度传感器则负责采集载体汽车的里程信息。通过以上两种传感器的合作，就可以使用积分算法，得到桥梁结构的线形，实现对桥梁结构线形的快速连续检测。

3.2 实验设计

使用别克SGM6530ATA为载体汽车，发动机类型为自然吸气四冲程直列四缸发动机。

如图3所示，实验选在某地下通道进行。该地下通道于2015年2月通车，路面状况良好，且每隔50米左右就有一条点状减速带，整个隧道总共五条点状减速带，减速带是线形所不需要体现出来的信息，属于噪声信号，且与路面不平的情况类似，可以用减速带代表这种高频较小幅值的振动类型。并且在使用Morlet小波进行时频分析的时候，很容易通过时间信息和载体汽车的速度信息相结合，然后得到位置信息。进而很容易区分出行驶在正常路面和经过减速带的数据。根据路面情况，可分为三个工况。

图3 某地下通道示意图

工况1：仅仅启动载体汽车的发动机，不松开手刹，将档位置于驻车档，保持车辆静止。用于分析载体车辆在仅发动机工作时产生的振动对光纤陀螺线形测量系统的影响的频域特点。

工况2：让载体车辆以发动机转速为900 r/min,车速为15 km/h的速度在隧道完好的路面上行驶，分析汽车在正常行驶过程中，陀螺采集到的数据的频域特征。用于对比工况1在频域上的异同。

工况3：让载体车辆以发动机转速为900 r/min,车速为15 km/h的速度行驶过隧道中的减速带。分析受外界影响所带来的噪声信号对陀螺线形测量系统的频域特点。用于对比工况1和工况2在频域上的异同。

工况1单独使用光纤陀螺线形测量系统采集信号，工况2和工况3则可以在同一次实验中采集，而在后续的数据处理中可以单独挑选出进行分析。

4 时频分析

光纤陀螺在隧道中采集到的原始信号如图4所示。

图4 光纤陀螺仪采集到的原始数据

由此可知，减速带等这类高频小幅值的振动，在时域中的表现与正常的路面并没有明显区别。难以分析出它们的特点，更难以对其进行有针对性的处理。为了找到此类振动噪声信号的特点，可以从频域出发，分析它们的频域特征。

选择复Morlet小波对工况1数据进行时频分析，并画出的时频图如图5所示。

图5 工况1时频分析

工况1在频域主要表现为在13.5 Hz和27 Hz左右持续并且稳定的存在较大的幅值。由汽车理论可知[4]，直列四缸发动机的振动和噪声主要是由基频和点火频率引起的点火扰动组成。点火扰动的主要阶数等于气缸数目的一半。由于载体车辆的发动机类型为直列四缸发动机，因此，载体车辆的发动机振动噪声的主要频率为发动机的基频和2倍频。而发动机的基频则跟发动机的转速有关，在仅仅启动发动机的状态下发动机的转速约为800 r/min，所以发动机的基频在13.5 Hz左右，进一步可知点火扰动为27 Hz左右，符合时频分析的结果。所以实验1中，光纤陀螺采集到的信号是由发动机产生。然而在实际的测量的过程中，发动机转速会大于或等于仅仅启动发动机时的转速。相应的，点火扰动所影响的频率也会大于或等于27 Hz。

使用Morlet小波对光纤陀螺采集的隧道信号进行时频分析，画出的时频图如下。

图6 隧道时频图

如图6所示，载体车辆在真实的测量过程中采集到的数据和仅仅启动发动机时的数据有明显差异。且在隧道中采集到工况2和工况3的数据在频域上也明显不同，说明光纤陀螺线形测量系统采集到的减速带所引起的这类高频小幅值的振动在时域上和正常路面的差异并不明显，但是在频域上则和正常路面有着较大的区别，有利于我们对光纤陀螺线形测量系统采集到的信号进行分析和处理。为了方便进一步的分析三种工况下的频域特点，从时间轴上选取有代表性的数据，在频域上进行比较和分析。

频段1(0～10 Hz)：如图7所示，工况1在此频段的数据几乎为0，说明载体汽车发动机的振动对该频段没有任何影响。而工况2和工况3在此频段表现较为一致，0～2 Hz幅值非常的大，然后逐步下降，到8 Hz左右接近于0。由此可知，此频段的信息来自于路面线形的数据，且不会受到载体汽车发动机和减速带引起的振动的影响。在后续的数据处理中，应该完整的保留此频段的信息。

图7 频段1

频段2(10～18 Hz)：如图8所示，工况1仅仅只在12～17 Hz有所起伏，且幅值相较于工况2和工况3都要小许多，影响的频段范围也较小。工况2在整个频段内起伏较为剧烈，幅值相较于工况1更大，影响的频段范围更广，但是相较于工况3较小，影响的范围也较窄。工况3在10～18 Hz整个频段内起伏剧烈，幅值非常大，影响的范围也最广。结合前文对工况1的分析可知，工况1为发动机所引起的振动带来的影响。工况2在10～18 Hz的表现则为发动机和路面线形共同影响的结果。而工况3在10～18 Hz的表现则为发动机振动，路面线形，减速带共同影响的结果。在后续的信号处理过程中，应该尽量减小发动机振动，减速带对此频段的影响，保留路面线形在此频段内的信息。

图8 频段2

频段3(18～27 Hz)：如图9所示，工况1在此区间内几乎为0，说明载体汽车发动机的振动对该频段没有任何影响。而工况2在此频段内有较小的起伏，结合前文分析和所处工况可知，这是由路面线形信息带来的影响。相对于工况1和工况2，工况3在此频段内幅值非常大，所以，这个频段内的数据则是由路面线形信息和减速带共同影响的结果，且减速带影响较大。在后续的数据处理过程中，应该尽量保留路面线形的信息，大幅度的减小减速带在此频段的影响。

图9 频段3

频段4(27 Hz及以上)：如图10所示，工况1和工况2在27 Hz及以后的频段表现相当一致，27 Hz左右出现较小的峰值，然后在逐渐下降，在35 Hz左右逐步降低至0。而工况3在此频段内，相较于工况1和工况2，在27 Hz左右的幅值大很多，然后也会逐步下降，但是并不会下降至0，而是在500-100之间来回抖动。结合前文对工况1的分析可知，工况1和工况2在27 Hz左右的峰值来自于发动机点火频率带来的点火扰动。而工况3中的峰值则源自于点火扰动和减速带共同影响的结果。27 Hz以上则是源自于减速带所带来的噪声信号。由此可知，27 Hz以上均为噪声信号，在后续的数据处理中可以采用数字滤波的方式将27 Hz以上的信号去除。

图10 频段4

为了保证光纤陀螺采集到的有效信息不受到影响，对于有效信息和噪声信号混叠的频率区域，应该使用减振装置或者使用平顺性更好的载体来提高测量精度。而对于无有效信息的频段，则可以采用数字滤波的方式去除噪声信号，提高测量精度。

5 数据处理及应用

某跨江大桥如图11所示，主桥为双塔双索面预应力混凝土梁斜拉桥，其中斜拉桥长728米。

图11 某跨江大桥

根据前文分析可知，27 Hz以上均为噪声信号，那么可以使用低通数字滤波的方式进行处理。这里我们选择切比雪夫低通滤波器对光纤陀螺线形测量系统采集到的数据进行处理。切比雪夫低通滤波器是现代数字信号处理中的经典滤波器，可以有效的去除信号中的高频分量的同时完整的保留低频分量。将切比雪夫低通滤波器的处理方法应用在该跨江大桥的实际测量中。首先对原始信号进行谱分析，由前文分析可知，27 Hz以上为噪声信号，于是以27 Hz为分界分为高频部分和低频部分，保留信号的低频项，舍弃掉高频项。最后再对滤波后的信号进行重构，就可以有效的去除27 Hz以上的噪声信号，提高信噪比。

如图12所示，切比雪夫低通滤波器有效的抑制了高于27 Hz的噪声信号，达到了降噪的目的。

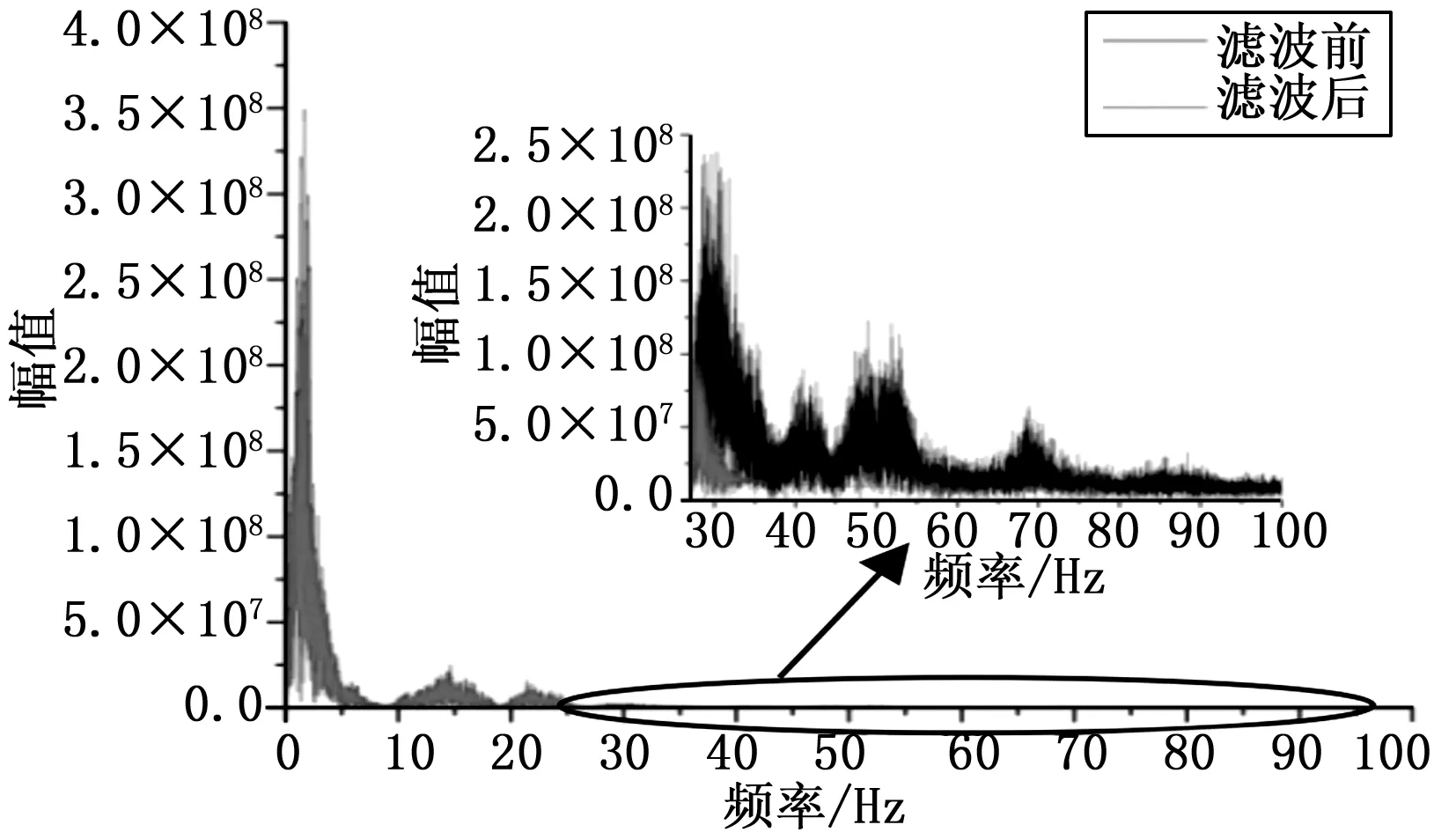
图12 幅频分析

把低通滤波处理前后所绘制桥梁结构线形与以水准仪为标准的数据进行对比，结果如图13所示。

图13 某跨江大桥斜拉桥线型

由此可知，在仅仅只针对原始数据处理，且无其他辅助手段优化测量精度的情况下，滤波前，跨中误差为18 cm，滤波后，跨中误差为9 cm。由此可知，切比雪夫低通滤波器可以有效地提高光纤线形测量系统的测量精度。

6 结束语

通过时频分析，可以分析出光纤陀螺桥梁线形测量设备在实际测量中不同工况下的频域特点。为使用其他辅助手段提高测量精度提供了理论基础。使用切比雪夫低通滤波器，去除掉噪声信号，可以有效的提高测量精度。在目前靠改进硬件设计来减小测量运载体的振动噪声误差在客观上困难越来越多，成本越来越高的情况下，使用数字信号处理的手段分析和解决光纤陀螺线形测量系统在实际检测中遇到的振动所带来的误差，效率高且易于实现。

[1] JTG/T J21-2011,公路桥梁承载能力检测评定规程[M].北京：人民交通出版社，2011.

[2] 杨小森，闫维明，陈彦江，等.基于倾角仪的桥梁挠度测试方法研究[J].土木工程学报，2010，43(S):105-111.

[3] 李 盛,胡文彬,杨 燕,等. 基于光纤陀螺的大跨桥梁连续线形检测技术研究[J]. 桥梁建设,2014(5):69-74.

[4] 吴光强.汽车理论.第2版[M].北京：人民交通出版社,2014.

[5] Alhasan A , White D J， De Brabanterb K.Continuous wavelet analysis of pavement profiles[J].Automation in Construction,2016,63,134-143.

[6] 程建华,李明月,时俊宇,等. 船用光纤陀螺小波实时滤波算法的设计与实现[J]. 传感器与微系统,2011(7):104-107,110.

[7] 魏明果.实用小波分析[M].北京：北京理工大学出版社，2005.

[8] Raul Ruiz de la Hermosa Gonzalez-Carrato.Pattern recognition by wavelet transforms using macro fiber composite transducers[J].Mechanical Systems and Signal Processing，2014,48.

Analysis of Influence from Vibration on FOG Based Measurement System

Zhang Zhen1,3,Yang Yan2,Zheng Lei2,Yang Dandan2,Gan Weibing3,Hu Wenbin2

(1.School of Information Engineering, Wuhan University of Technology, Wuhan 430070, China; 2.State Engineering Laboratory for Fiber Optic Sensing Technology,Wuhan University of Technology,Wuhan 430070,China；3.Ministerial Key Laboratory of Fiber Optic Sensing Technology and Information Processing，Wuhan University of Technology,Wuhan 430070,China)

In process of measuring the line-shape of bridge structure by FOG based measurement system,as the line-shape is calculated by the integral algorithm, the vibration and shock from vehicle and rode surface can result in large measurement error. And the error will be accumulated with the increase of measurement time and distance, showing the characteristics of divergence. In order to reduce the influence from vibration and shock, obtaining location and traffic information through the data of time and speed with the means of time-frequency analysis, and then getting the frequency characteristics of different road conditions. Choosing a flat road with a dotted speed bump to complete the experiment, then finding different road conditions will bring in different frequency domain characteristics, also finding the signal above 27 Hz is noise by time-frequency analysis with Morlet Wavelet Transform. At last, taking a River Bridge as an example, processing FOG signal with Chebyshev low-pass filter to remove the noise signal higher than 27 Hz, and results show that the measurement precision have been improved by 50%.

FOG；bridge structure measurement；signal processing；vibration；Morlet wavelet；Chebyshev filter

2017-02-06；

2017-03-03。

国家自然科学基金资助项目(61402435)；中央高校基本科研业务费专项资金资助项目(2014-IV-090)。

张 震(1992- )，湖北武汉人，硕士，主要从事光纤传感技术方向的研究。

1671-4598(2017)08-0015-05

10.16526/j.cnki.11-4762/tp.2017.08.005

TN253；TB22

A