基于多叉树的梯形图向指令表转换算法

周伟强，何通能，陈德富

(浙江工业大学 信息工程学院，杭州 310023)

基于多叉树的梯形图向指令表转换算法

周伟强，何通能，陈德富

(浙江工业大学 信息工程学院，杭州 310023)

针对目前可编程逻辑控制器(PLC)编辑软件中梯形图向指令表转化算法的缺陷，通过对梯形图语言的分析与研究，并考虑到梯形图和指令表在实际应用时的优劣点，提出了一种借助多叉树来实现PLC梯形图向指令表转换的算法;该算法采取从左至右，从上至下的扫描原则将梯形图构建成多叉树，借助多叉树来反应图符间的逻辑关系，然后通过后序遍历多叉树来得到指令表程序;此算法在处理多重串并联结构梯形图时具有更高的效率，同时适用于堆栈指令，使得该算法具有更好的通用性。

可编程逻辑控制器;梯形图;指令表;多叉树

0 引言

可编程逻辑控制器即Programmable Logic Controller(以下简称PLC)，是一种专门为在工业环境下应用而设计的现代化自动控制设备[1]，广泛应用于各种类型的控制系统中，主要功能包括控制、计数、数据采集和通信联网等。

为了适应广大工程设计人员的编程习惯，国际电工委员会设计制定了PLC编程语言的标准——IEC 61131-3。该标准规定了PLC的编程语言包括梯形图(LD)、指令表(IL)、功能模块图(FBD)、顺序功能流程图(SFC)和结构化文本(ST)共五种。其中主要由母线、触点和线圈等构成的梯形图简明易懂，使用梯形图编写的PLC程序易于理解，从而使梯形图成为PLC的主要编程语言[2]。但是，梯形图只是形象得展示了电器元件之间的组合逻辑关系，无法被PLC识别并直接运行，而PLC所能识别运行的目标代码一般由指令表转化而来。因此通过转换算法将梯形图转换为指令表，并将其运用在PLC上位开发系统中，这样就省去了人工对梯形图的翻译工作，提高了开发的效率。

通过对梯形图设计规则和指令表编程规则进行的研究分析，并参考了传统的拓扑排序和二叉树遍历等一系列算法的不足之后，提出了基于多叉树的梯形图向指令表转换的算法。

1 梯形图和指令表

梯形图是以触点符号代替传统电气控制回路中的按钮开关、接触器、继电器触点等部件的一种编程语言，是目前使用最多的一种PLC编程语言。其设计与编写梯形图语言时应注意以下规则：1)继电器的触点应画在横线上，不可以画在竖线上，绘制梯形图时应依照从左至右、从上至下的原则；2)没有触点的线路应置于垂直方向，不能置于水平方向，这样有利于分辨触点的逻辑组合以及逻辑结果；3)依照左重右轻、上重下轻的原则，即出现若干串联模块并联时应将触点最多的那条线路放在梯形图的上方，而当若干并联模块串联时应将触点最多的那个并联模块放在梯形图的左边；4)线圈放在梯形图的最右边，触点必须放在线圈的左边[3]。

指令表也称为语句表，是一种助记符表达式，与汇编语言中的指令类似。它将一系列操作指令(助记符)组成的控制流程，通过编程器存入PLC中[4]。指令表的每条指令是由操作码和操作数两部分组成的，操作码是指令的助记符，操作数是功能指令所作用的数据，包括继电器编号、定时器/计数器配置值和常数等。虽然梯形图的优点是形象、直观、实用，为广大电气技术人员所接受，但是难以将其直接转化为PLC能直接运行的代码，而指令表可以直接编译为PLC的可执行代码。在PLC软件的开发过程中，实现梯形图向指令表的转换是必不可少的一部分，使得PLC软件可以在最后通过对指令表的编译或解释执行来实现PLC控制程序的运行[5]。

目前已有一些文献给出了梯形图向指令表转换的算法，如文献[6]中先将梯形图映射为AOV图运用了拓扑排序算法。该算法的优点是有良好的算法效率，时间复杂度为O(n+e)，其中n表示AOV网顶点的个数，e表示弧的个数，但是该算法过于依赖梯形图本身的图符含义，当梯形图的串并联关系较为复杂时转化不稳定，且存在误判的可能，通用性较差。文献[7]和文献[8]提出了基于AOV网及二叉树的转换算法，该算法在处理串并联结构复杂的梯形图时，借助二叉树建立了过多的逻辑节点，占用了过多的空间，使得算法的遍历效率也因此下降，同时该算法不适用于存在堆栈指令的梯形图程序。文献[9]中虽然借助串并联归并清晰地表示了梯形图的层次，但并没有提高遍历的效率。

通过研究传统转换算法的缺陷与不足，从而提出了一种基于多叉树的梯形图向指令表转换的算法，从左至右，从上至下扫描梯形图，将梯形图各元件之间的逻辑关系转换为多叉树数结构，然后对多叉树进行后序遍历得到指令表。该算法在多重串并联梯形图程序中，与使用二叉树结构相比，有效得减少了逻辑节点的个数，从而提升了算法效率，同时也适用于具有堆栈指令的梯形图程序，使得该转换算法具有更好的通用性，且不会出现传统拓扑排序算法中串并联误判的情况。

2 多叉树

树是一些节点(node)的集合。这个集合可以是空集；若不是空集，则树由称做根(root)的节点r以及0或多个非空的(子)树T1，T2，…，Tk组成，这些子树中每一棵的根都被来自根r的一条有向的边(edge)所连接。当树的每个节点最多只有两棵子树时，称为二叉树，而任一节点的子树多于两棵时，称为多叉树。

实现树的一种方法是在每一个节点除数据外还要有一些链，使得该节点的每一个儿子都被一个链所链接。然而，由于每个节点的儿子树可以变化很大并且事先不知道，因此在数据结构中建立到各子节点的直接链接是不可行的，因为这样会产生太多浪费的空间。解决方法为将每个节点的所有儿子都放在树节点的链表中，一般的多叉树数据结构如下：

struct TreeNode

{

Int NodeType; //多叉树节点的基本信息

TreeNode *firstChild; //指向儿子的指针

TreeNode *nextSibling; //指向兄弟的指针

}

通过对PLC梯形图程序编写原则的分析可得，用梯形图编程的过程实质上就是利用梯形图图符来表示功能元件，借助图符间的连接方式来表示功能元件之间的串并联结构及逻辑关系[10]。考虑到梯形图的图符元件代表着指令表中的功能指令，因此将PLC的梯形图程序转化为指令表程序一定是有规律可循的。

通过研究发现梯形图中每个梯级的图符之间的串并联关系是一种层次结构，而这种层次结构可以用数据结构中的树来表达，而且借助多叉树表达一个梯级中图符之间的逻辑关系之后，那么整个梯形图就是多个树的集合，也就是森林。而扫描梯形图，就是一个构建树和森林的过程。树由一个根节点和若干棵子树构成，这若干根子树中每一棵都有一个根节点和它自己的子树。这里用树的叶节点代表具体的元件，而用非叶节点表示其左右子树的逻辑结合方式[11]。

3 由梯形图建立多叉树算法的主要步骤

在梯形图向指令表转换的过程中，通过梯形图建立多叉树是最为关键的一部分[12]。构造多叉树以先左后右，先上后下为原则对每一行梯形图进行遍历，当扫描完一个节点后若没有发现竖线就一直向右扫描，若扫描到竖线记录其位置且处理完并联节点后继续向右扫描，直到扫描到最后一个节点为止。

3.1 算法的主要步骤

S1：自左向右进行遍历，每扫描到一条竖线就记下该竖线的位置以及之前遍历的节点，记录此时遍历的节点数目，新建一个“与”节点(若此前只遍历了1个节点则新建一个“或”节点)，将之前遍历的节点作为该“与”节点的子节点，这些子节点自左向右的排列顺序必须与遍历的顺序一致。若该“与”节点不是所在行最后的节点，则将该新建的“与”节点视为后续节点的子节点，从而继续构造多叉树，然后转S2处理竖线；若该“与”节点是所在行最后的节点，则判断是否还有记录的竖线未处理，若无则终止算法，若有则说明出现了多重输出的情况，转S8。

S2：当扫描到竖线时，用标志位记录该列竖线的数量(竖线的数量即为竖线所占的行数)。根据竖线位置，以先右后左的原则进行遍历。从竖线的位置(即竖线所在的坐标)开始向左扫描，判断是否存在节点，若有则转S3，否则转S6。

S3：新建一个“或”节点(该节点为上一个节点的父节点，即上一行梯形图所构建的子树的根节点)并继续向左扫描，当扫描到竖线时，判断该竖线是向上还是向下，若为向上的竖线，则转S4，否则转S5。

S4：根据该行遍历的节点数目，类比步骤S1的方式建立“与”节点，且该“与”节点作为之前“或”节点的子节点，然后转S1继续向右扫描。

S5：记录该竖线的位置，转S7。

S6：此时由于竖线的左边没有节点，表明竖线的右边存在元件，新建一个“与”节点，并将该节点作为已经构建完成的多叉树的根节点，记录该竖线的位置，返回该竖线的上一行转S1开始继续向右扫描(将已经构建的多叉树的根节点作为后续“与”节点的子节点)。

S7：当竖线标志位的值(即该列竖线的数量)大于等于1时，将该标志位减1，并将扫描的初始位置放至下一行，并转S3；若标志位的值等于0时，表明该并联块已经处理完毕，根据记录的竖线位置，转S1开始继续向右扫描(将已经构建的多叉树的根节点作为后续“与”节点的子节点)。

S8：判断该竖线所占的行数，添加堆栈节点并逐行扫描转换节点，直至结束。

注意：

1) 在构建多叉树时，若是从左至右扫描，兄弟节点则按照扫描的顺序从左至右依次排列；若是从右至左扫描，兄弟节点则是从右至左依次排列。

2) 当出现竖线嵌套时，类比堆栈的原则，优先处理后扫描到的竖线所在的行，之后处理先扫描到的竖线所在的行。

3) 当父节点与子节点为同一种逻辑节点(即“与”节点和“或”节点)时，则删去该逻辑子节点，并直接将被删去的逻辑子节点的相应叶节点作为逻辑父节点的子节点。

4)S8中，在第一行竖线起始位置添加进栈指令(MPS)，中间行(行数小于3则不添加读栈指令)起始位置添加读栈指令(MPD)，最后一行起始位置设置出栈指令(MPP)。

通过以上方法就完成了梯形图向多叉树的结构转换，而构建完成的多叉树主要反映了梯形图图符间的串并联关系，要得到指令表还需进一步转化。其中该多叉树的叶子节点必定是图符元件，而逻辑节点必定都是非叶节点。

3.2 多叉树转化为指令表

经过扫描和错误检查后，对构建完成的多叉树进行遍历即可将梯形图转化为指令表。根据构造多叉树时图符元件与逻辑节点之间的位置关系可以得到，应该对多叉树采取后序遍历的方式。即先遍历左子树，然后依次遍历右子树，最后遍历根节点。但是在遍历完成后需要考虑到堆栈指令的问题，即出现多重输出指令时，需要自动识别并添加堆栈指令MPS与MPP。

直接对多叉树进行后序遍历得到原始指令表只是表明了图符间的逻辑结构，但不符合指令表语言的编程规范，需要在遍历时添加判断条件，从而得到最终可以直接转换为十六进制目标代码的指令表程序，具体转换原则见第4章。

4 基于多叉树的梯形图向指令表转换的实例

如图1所示为一个梯形图程序，该程序中包含了多重串、并联的关系，且由于是多重输出(即包含了Y0和Y1)，因此需要使用堆栈指令进行入栈出栈的操作(传统借助AOV图进行拓扑排序或者转化为二叉树的算法不能适用)。

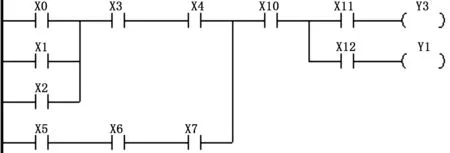
图1 梯形图程序

根据第3章中说明的算法，从母线开始向右扫描，当扫描到常开触点X0右边的竖线时，建立一个“或”节点，用符号“+”表示，并将节点“X0”作为该“或”节点的左子节点。由于扫描到的竖线占据两行，因此本该新建一个“或”节点作为节点“X0”的兄弟节点，但由于父节点也为“或”节点，因此省略，接着依次扫描X1和X2建立元件节点并将其作为“或”节点的子节点。如图2所示即为X0、X1和X2所构成的第一个并联块所构建的多叉树。

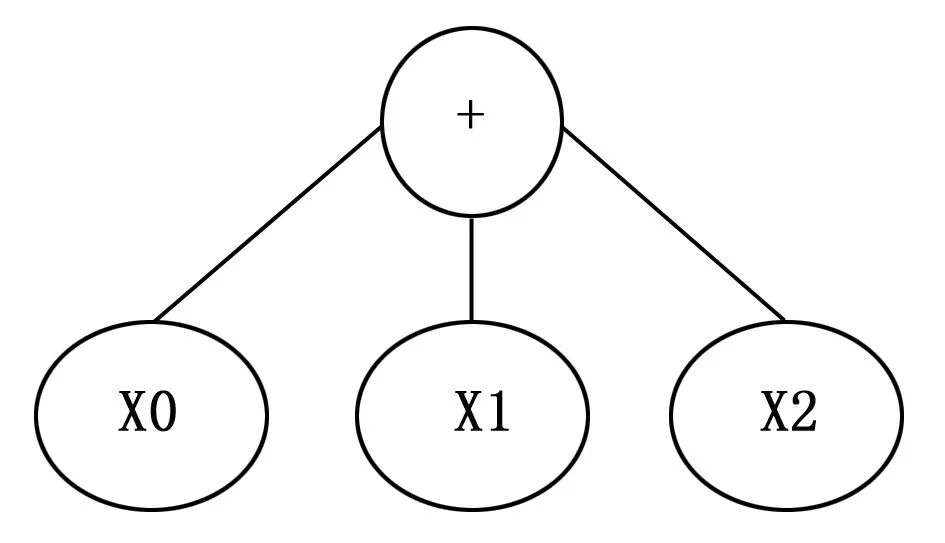
图2 并联块X0X1X2构建的多叉树

建立完图2所示多叉树后，继续回到主线路向右扫描直至常开触点X4右边的竖线，此时新建一个“与”节点，用“*”表示，将之前由X0、X1和X2构建的多叉树作为该“与”节点的左子树，之后建立元件节点“X3”和“X4”并分别将其作为该“与”节点的子节点。

然后开始处理竖线，先建立一个“或”节点，并将之前构建好的多叉树作为该“或”节点的左子树，然后扫描X5、X6和X7所在的行，当扫描到向上的竖线时，该行的扫描结束。根据扫描结果新建一个“与”节点，将其作为处理竖线时新建的“或”节点的右子节点，然后将元件节点“X5”、“X6”和“X7”依次从左至右作为该“与”节点的子节点。如图3所示即为并联块X0X1X2、串联块X3X4以及串联块X5X6X7共同构建的多叉树。

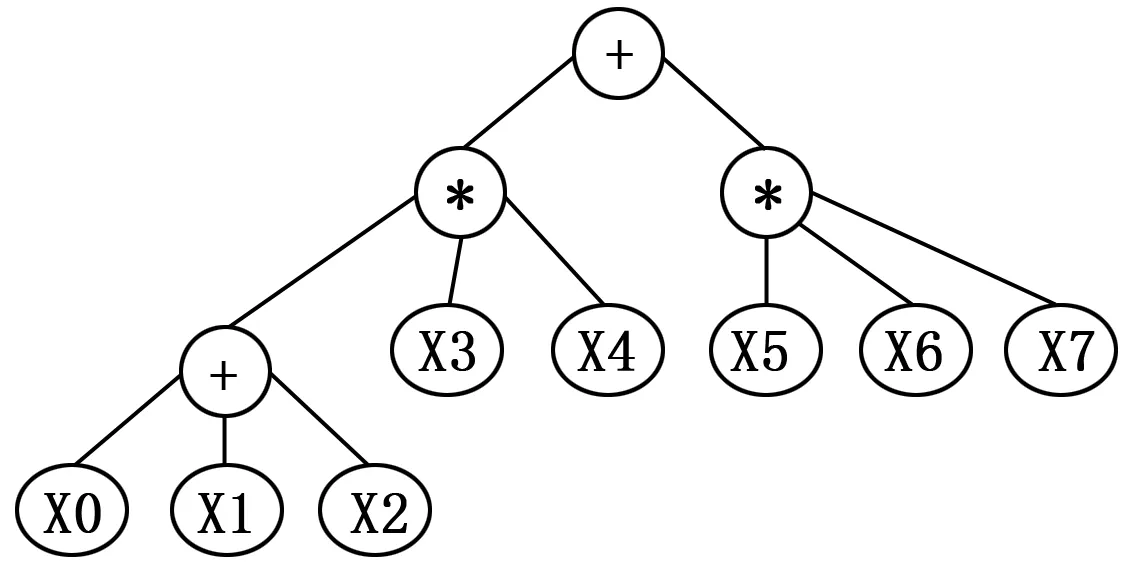
图3 并联块X0X1X2、串联块X3X4和串联块X5X6X7构建的多叉树

回到主线路继续向右扫描，当扫描至常开触点X10右边的竖线时，新建一个“与”节点，将之前构建的多叉树作为该“与”节点的左子树，同时将元件节点“X10”作为该“与”节点的右子节点。接着开始处理竖线，发现竖线左边没有元件，记录该竖线位置后返回主线路继续向右扫描直至Y0，此时发现Y0的右边没有竖线，表明出现了堆栈指令。因此新建进栈指令节点“MPS”，元件节点“X11”以及输出节点“Y0”，依次从左至右排列作为之前“与”节点的子节点。最后处理下一行，即新建出栈指令节点“MPP”，元件节点“X12”和输出节点“Y1”。最终遍历图1梯形图构建的多叉树如图4所示。

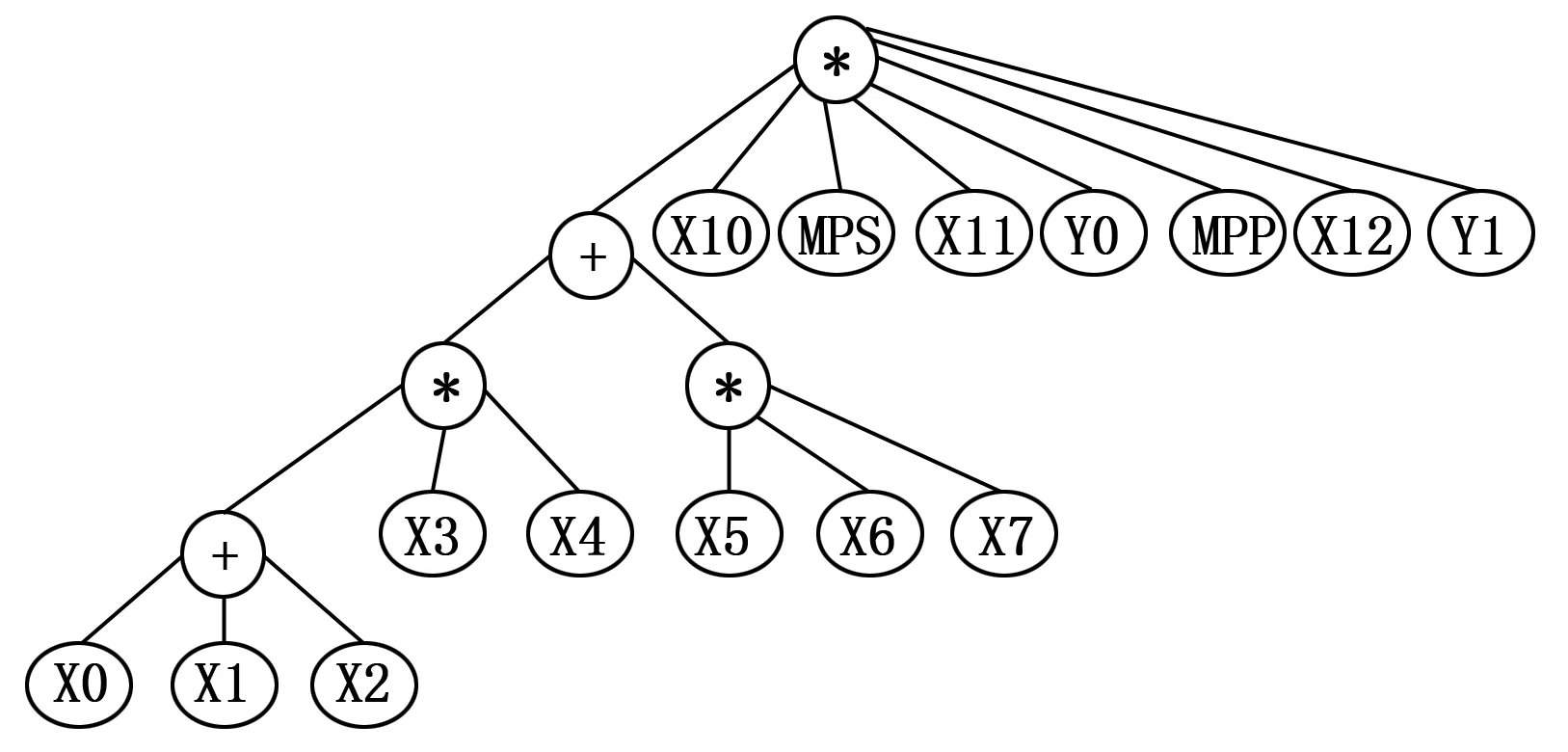
图4 遍历梯形图构建的多叉树

将梯形图转化为多叉树之后，如果直接对图4的多叉树进行后续遍历而不加以区分的话，则会得到如下所示的原始指令表程序：

LD X0

LD X1

LD X2

OR

LD X3

LD X4

AND

LD X5

LD X6

LD X7

AND

OR

LD X10

MPS

LD X11

OUT Y0

MPP

LD X12

OUT Y1

AND

该原始指令表程序虽然清晰的反应了图符间的逻辑结构，但是不符合指令表语言的编程规范，因此在后序遍历时加入判断条件，从而得到符合指令表语言编程规范的程序。具体的判断原则的如下所示：

1)若为触点元件，且为父节点的第一个子节点，则其生成指令的操作码为LD(若为常闭触点则为LDI)；

2)若为触点元件，且不为父节点的第一个子节点，则其生成指令的操作码与父节点的逻辑类型相同，即父节点为“与”节点则为AND，父节点为“或”节点则为OR(若为常闭触点则分别为ANI或ORI)；

3)若为逻辑节点，且为父节点的第一个子节点，则不生成指令(若没有父节点，即为根节点时也不生成指令)；

4)若为逻辑节点，且不为父节点的第一个子节点，则其生成指令的操作码与父节点的逻辑类型相同，即父节点为“与”节点则为ANB，父节点为“或”节点则为ORB。

根据以上原则对图4多叉树进行后序遍历得到的符合编程规范的最终指令表如下所示：

LD X0

OR X1

OR X2

AND X3

AND X4

LD X5

AND X6

AND X7

ORB

AND X10

MPS

AND X11

OUT Y0

MPP

AND X12

OUT Y1

5 结束语

研究分析了梯形图节点元件互相之间的逻辑关系，借助多叉树特殊的数据结构来反应图符之间的逻辑关系并完成梯形图向指令表的转换。在自主开发的梯形图编译软件上成功应用了该梯形图向指令表转换的算法，表明其能够正确地将用户的梯形图程序转换为指令表程序。该算法可用于逻辑复杂梯形图向指令表的转换，即使出现堆栈指令也能同样适用，且梯形图的扫描过程不重复、不遗漏。构建完多叉树之后的遍历过程相较遍历二叉树等也更为高效。

[1] 李金城. 三菱FX2NPLC功能指令应用详解[M]. 北京:电子工业出版社, 2011.

[2] 吕俊白, 施敏芳. PLC梯形图可视化编辑与语句表的自动生成[J]. 自动化仪表, 2005, 26(3): 28-30.

[3] 韩雪涛, 韩广兴. 双色图解PLC梯形图及语句表[M]. 北京:人民邮电出版社, 2012.

[4] 阳俊将, 黄道平, 刘少君. 关于PLC梯形图到指令表转换算法的研究[J]. 信息技术, 2012, (6): 75-78.

[5] 未庆超, 蔡启仲. 基于ARM的PLC编译系统设计[J]. 计算机测量与控制, 2014, 22(4): 1225-1229.

[6] 崔小乐, 周卓岑. 可编程控制器的梯形图语言与语句表语言的互换算法[J]. 微电子学与计算机, 2000(1): 26-30.

[7] 葛 芬, 吴 宁. 基于AOV图及二叉树的梯形图与指令表互换算法[J]. 南京航空航天大学学报, 2006, 38(6): 754-758.

[8] 黄晶晶, 陈文芗. 基于二叉树的PLC梯形图转化为指令表的算法[J]. 现代电子技术, 2010(4): 125-134.

[9] 傅 亮, 胡飞虎. 基于串并联归并的PLC梯形图向指令表转换算法[J]. 计算机工程与应用, 2009, 45(27): 72-118.

[10] 莫易敏, 章德平. PLC梯形图转化为指令表算法及实现[J]. 控制工程, 2006, 13(6): 573-576.

[11] 石 锐, 周 雷, 杨正益. 软PLC梯形图到语句表转换新策略的研究[J]. 计算机工程与应用, 2010, 46(18): 244-248.

[12] 谭锦洁, 程良鸿, 殷学鹏. 嵌入式PLC中梯形图到AOV图的映射[J]. 计算机测量与控制, 2004, 12(10): 993-1004.

Transformation Algorithm from Ladder Diagram to Instruction List Based on Multi-tree

Zhou Weiqiang, He Tongneng, Chen Defu

(College of Information and Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Aiming at the shortcomings of the transformation algorithm from ladder diagram to instruction list in the current programmable logic controller(PLC) editing software, this paper presents an algorithm to realize the transformation from PLC ladder diagram to instruction list based on multi-tree. Through the analysis and research of ladder diagram, shows the advantages and disadvantages of the ladder diagram and instruction list in practical application. The multi-tree data structure is created following the scanning principle that from left to right, from top to bottom. And the multi-tree is used to reflect the logical relationship between the diagrams. Then get the instruction list by post-traversing the multi-tree.This algorithm has higher efficiency when dealing with the ladder diagram which has multiple series-parallel structures. And it is also suitable for the stack instruction, which makes the algorithm more versatile.

programmable logic controller; ladder diagram; instruction list; multi-tree

2017-02-18；

2017-03-05。

周伟强(1990-)，男，浙江海宁人，硕士研究生，主要从事控制科学嵌入式方向的研究。

1671-4598(2017)08-0191-04

10.16526/j.cnki.11-4762/tp.2017.08.049

TP273

A