基于轮轨时变接触刚度的车辆−轨道系统垂向振动分析

贺天龙，陈宪麦，徐磊



基于轮轨时变接触刚度的车辆−轨道系统垂向振动分析

贺天龙1, 2，陈宪麦1, 2，徐磊3

(1. 中南大学土木工程学院，湖南长沙，410075；2. 高速铁路建造技术国家工程实验室，湖南长沙，410075；3. 西南交通大学牵引动力国家重点实验室，四川成都，610031)

采用轮轨时变接触刚度代替轮轨非线性接触力的动力效应，模拟轮轨之间的自然接触状态，将有限元理论和能量变分法用于建立车辆−轨道系统垂向统一方程。通过输入脉冲型短波及中、长波不平顺激励，计算系统的动力响应，验证本文模型的正确性，并与国内常用的轮轨密贴模型进行比较分析。研究结果表明：轮轨密贴模型在分析中、长波不平顺激励工况下的系统动力响应是可行的；但在短波不平顺激励工况下，轮轨之间的刚性处理方法将放大短波激励效应，车轮“跳轨”处理方法尚需改进。

车辆−轨道耦合系统；时变接触刚度；垂向振动；能量变分法；统一方程

车辆−轨道系统的耦合振动分析是铁路动力学领域非常重要的研究内容，国内的车/轨系统动力学建模工作以车辆−轨道耦合动力学[1]为基本理论指导，已日趋完善。针对车辆−轨道系统的横向相互作用，应该考虑非线性蠕滑力及轮轨横向相对位移。然而，对于车辆−轨道系统的垂向相互作用，国内主要采用轮轨密贴[2−4]和轮轨弹性接触(基于Hertz非线性接触理论)[1]这2种建模方法。由于铁路钢轨存在的磨耗、扣件失效、轨道板离缝及路基沉降等一系列铁路轨道基础结构动态性能演变问题都与车/轨系统的垂向动力作用密切相关，所以，有必要对这2种垂向轮轨关系作用下的系统动力响应进行比较分析。为此，本文作者基于有限元方法对不同铁路线路工况的强模拟性能及求解轨道结构任意位置的动力响应，采用有限元方法，同时考虑轮轨之间的弹性接触刚度(即考虑轮轨相对位移)，以板式轨道结构为例，对这2种垂向轮轨关系进行计算。实际上，人们对轨道的有限元动力进行了大量研究，如：罗震等[5]基于多刚体系统动力学原理建立了车辆动力学计算模型，以梁−板−板有限元模拟板式轨道，通过轮轨界面形成车/轨系统的动态耦合，分别采用新型快速显示积分方法[6]和Newmark-β法[7]求解了车辆系统和轨道系统的动力响应；向俊等[8]采用横向有限条和板段单元模型分析了车/轨垂向动力响应，在正常行车时为轮轨密贴，而在车轮跳轨时，考虑轮轨相对位移。此外，人们在考虑轮轨接触弹性时，常将轮轨非线性接触弹簧时不变等效成线性化处理[9−12]。这些方法均没有在轮轨接触非线性、有限元方法及动力系统方程的统一求解上达到统一。本文作者采用轮/轨时变接触刚度的方法模拟轮轨之间的自然接触状态，通过能量变分和有限元建立车辆−轨道系统的统一方程，验证模型的正确性。建立能考虑车轮“跳轨”的轮轨密贴模型，比较本文模型与轮轨密贴模型在脉冲型短波及中、长波不平顺激励下的系统动力响应。

1 垂向耦合动力学模型

将车辆−板式轨道作为一个整体，建立如图1所示的车辆−板式轨道垂向耦合动力学模型。高速车辆模型采用具有二系悬挂的车辆模型。板式轨道因其结构左右对称，可取一股轨道进行研究，以钢轨模拟无限长且离散黏弹性点支承的Bernoulli−Euler梁，弹性支承在钢轨扣件处的轨下衬垫上；将轨道板模拟成连续黏弹性支承的有限长Bernoulli-Euler梁，CA砂浆等效为连续分布线性弹簧和阻尼器。

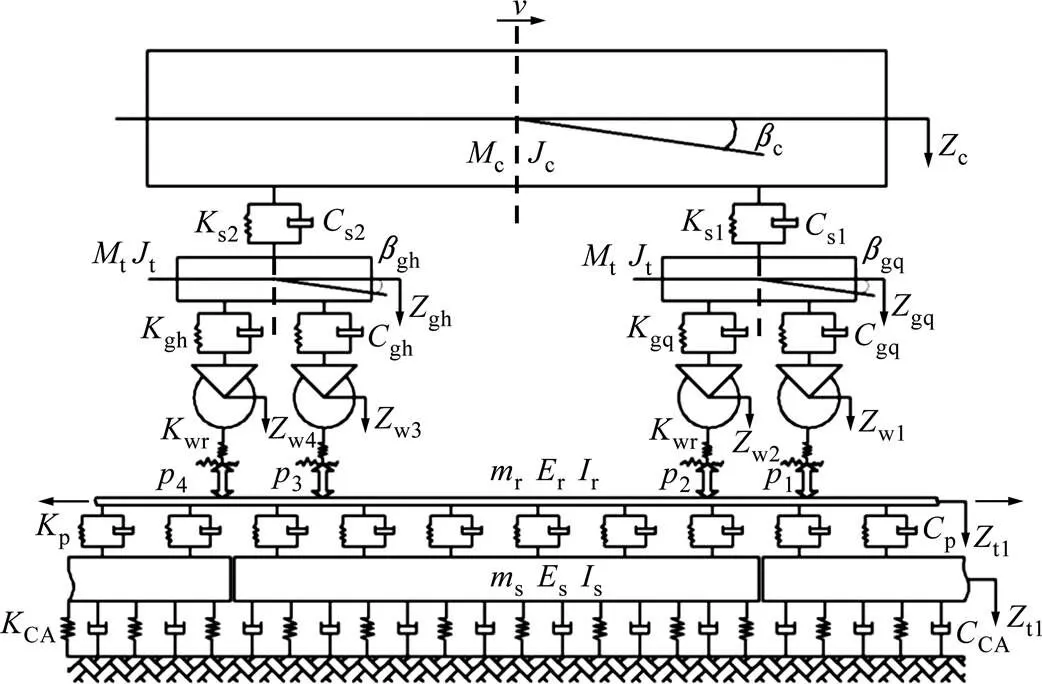
图1 车辆−板式轨道垂向耦合动力学模型

2 垂向耦合振动方程的建立

对于车/轨系统的垂向或横向振动，轮轨相互作用力确是车辆−轨道系统的内力，翟婉明[1]将每一积分步的轮轨力“显示”表达，分别将其作用于车辆系统与轨道系统，获得了与实测值接近的结果，得到广泛应用。曾庆元[2]认为轮轨相互作用力是“隐式”的，由于轮轨作用力与轮轨相对位移存在强非线性关系，对轮轨作用力在相对位移上的做功无法有效地进行一阶变分，只能采用轮轨密贴及线性蠕滑的假定。

在车−轨(桥)系统的数值积分步长内，所有的力及动力参数是基本不变的。本文假定轮轨之间存在1个轮/轨接触弹簧，随着积分步变化，其接触弹簧刚度是时变的，但在1个积分步长内，认为此弹簧接触刚度为定值，这符合轮轨之间的真实接触状态。

2.1 轮轨接触关系的处理方法

2.1.1 轮轨时变接触刚度模型

根据Hertz非线性弹性接触理论，可以确定轮轨之间的相互作用力()为

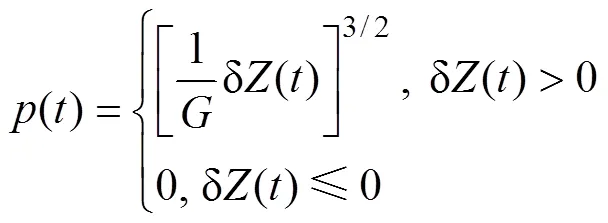
式中：为轮轨接触常数(m/N2/3)；δ()为轮轨间的弹性压缩量(m)。采用磨耗型踏面车轮，则

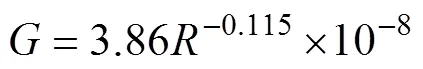
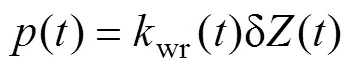
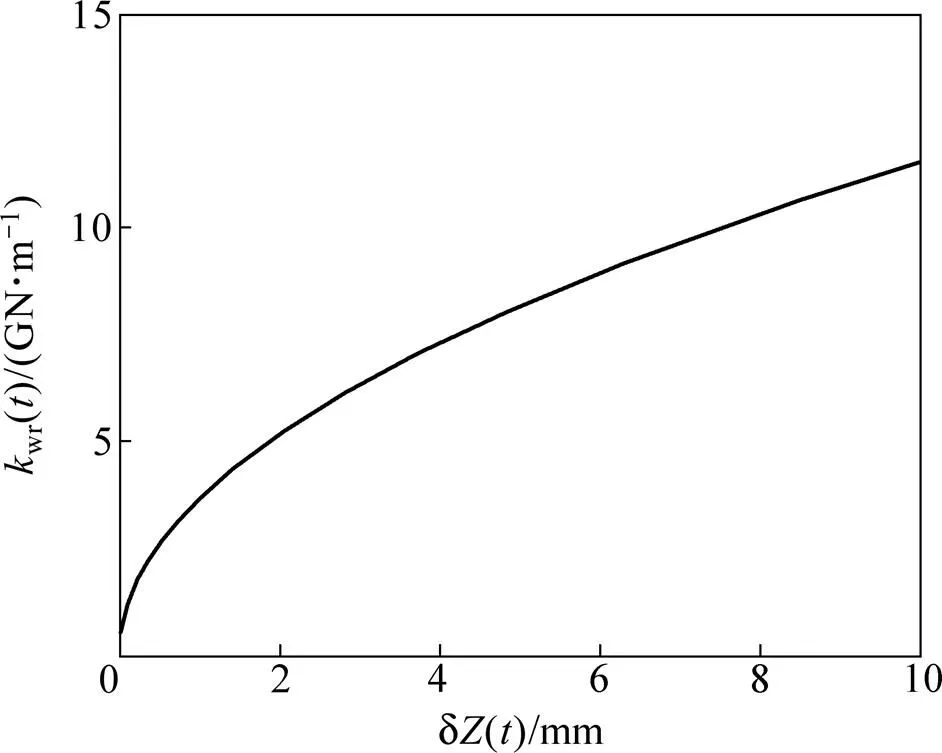
图2 轮轨时变接触刚度与轮轨相对位移kwr(t)的关系

轮轨时变接触刚度的计算基于Hertz非线性接触理论，这种方法完全将车辆系统与轨道系统耦合成一个整体，轮轨之间的弹性变形能可由轮轨接触刚度和轮轨相对位移计算获得。这是一种轮轨力“隐式”表达的方法，轮轨力作为轮轨之间的相互作用力是车辆−轨道系统的1个内力。当采用能量原理建立系统的平衡方程时，只需将轮轨变形能计入系统总能量即可，这兼顾了轮轨非线性接触本质和振动方程解适定性的要求[13]。

2.1.2 轮轨密贴模型

曾庆元等[2−3]采用的模型均为轮轨密贴模型。曾庆元[2]认为轨道不平顺不是时间的函数，轨道不平顺附加速度及加速度均为0 m/s2；娄平等[3]采用较复杂的轮轨约束方程，不仅考虑了轨道不平顺的附加速度及加速度项，而且加入了形函数矩阵的时间求导项。本文在文献[3]的基础上，采用简化的轮轨约束方程：

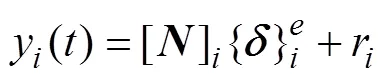
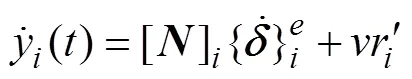
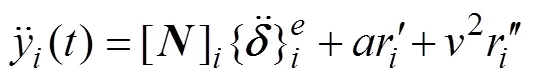
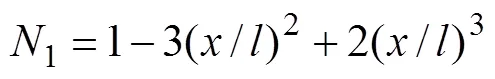
轮轨密贴模型在时域数值积分过程中，轮轨力是不计算和代入系统动力方程荷载列阵的。其轮轨力可根据每一步的计算结果，基于达朗贝尔原理进行计算：

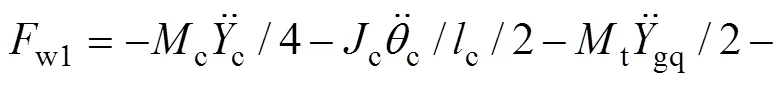
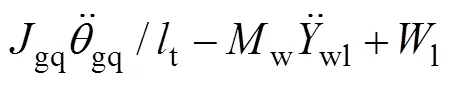
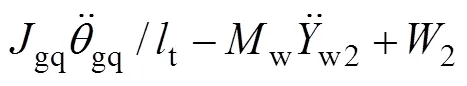
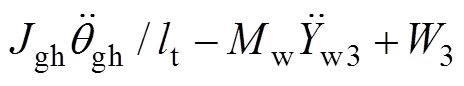
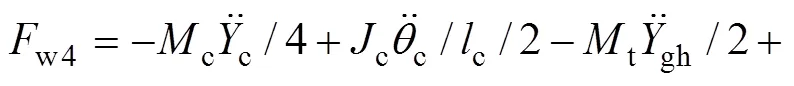
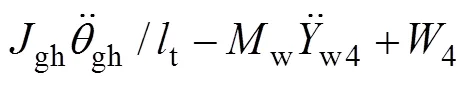
式中：w1，w2，w3和w4分别为第1~4轮/轨接触力；1，2，3和4分别为第1~4轮对的静轮载；其他变量含义见文献[1]。

2.2 车辆和轨道系统矩阵的建立

2.2.1 Hamilton原理

Hamilton原理是力学中应用最广泛和最重要的积分形式的变分原理，提供了从所有可能运动中找出真实运动的1个准则。对于完整的保守系统，Hamilton最小作用量原理定义为[14]

式中：为拉格朗日泛函。实际上，从Hamilton最小作用量原理成立的基本条件来说，由于车/轨系统存在黏滞阻尼力、库仑摩擦力及干扰力等非有势力，不再符合上述Hamilton完整保守系统的定义。但当积分时间足够小(1→0)时，进行瞬时处理。在某一瞬时，所有的内外力及应力是不变的，只产生满足势能驻值原理[15]的位移及应变，此时，非有势力(黏滞阻尼力、摩擦力及干扰力)可近似作有势力处理。曾庆元[16]基于这种瞬时状态的理想化处理，建立了弹性系统动力学总势能不变值原理，在车辆−轨道(桥梁)振动分析领域获得了广泛应用。这里的拉格朗日泛函可为

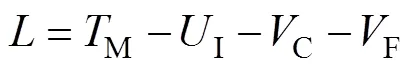
式中：M为系统的动能；I为系统的弹性势能；C为系统的阻尼力势能；F为外力势能。

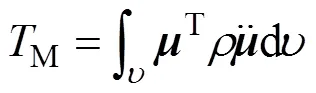
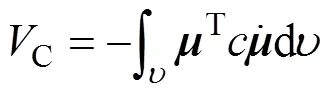
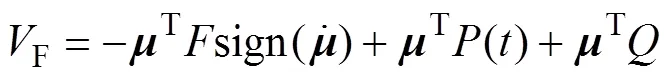
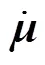
由式(3)可得

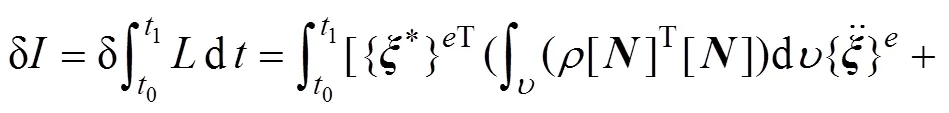
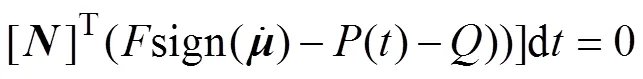
根据式(9)的基本表达形式及“对号入座”法则[2]，可以建立车辆和轨道的系统矩阵。

2.2.2 车辆系统矩阵

车辆系统的动力矩阵可参考文献[17]中的方法获得。这里以车辆系统刚度矩阵为例，简单说明其形成过程。在车辆－轨道系统的时域数值积分过程中，将轮轨之间的接触弹性变形能在车辆系统矩阵的分析过程中予以考虑。

车辆系统的初始振动位移参数列阵如下：

式中：c，gq和gh分别为车体、前构架、后构架的沉浮自由度；c，gq和gh分别为车体、前构架、后构架的点头自由度；w1，w2，w3和w4为第1~4轮对的沉浮自由度；r1，r2，r3和r4为第1~4轮对对应的钢轨振动位移；irr1，irr2，irr3和irr4为第1~4轮对对应的轨道垂向不平顺。

需指出的是：钢轨振动位移及轨道不平顺在原则上是属于轨道系统的振动位移参数，本文为编制程序方便，将轮轨接触点处对应轮对位移、钢轨位移及钢轨不平顺均纳入车辆系统中。

对于多刚体的车辆系统，其刚度矩阵的形成主要通过弹簧单元变形能的位移变分获得，故本文的车辆系统共10弹簧变形单元，如车体与前构架、前构架与第1轮对、第1轮/轨接触弹簧的弹性变形能(以弹簧受压为正)分别为

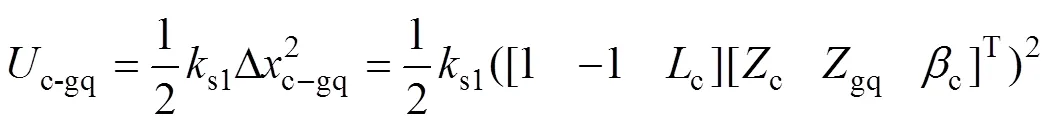
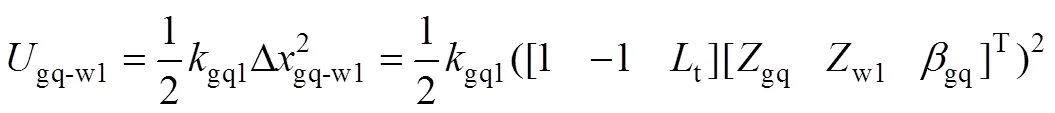
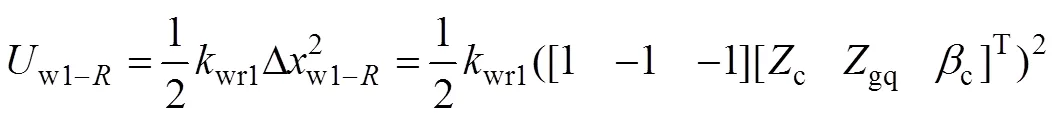
式中：s1，gq1和wr1分别为车体与前构架、前构架与第1轮对、第1轮/轨接触点之间的弹簧刚度；c和t分别为车辆二构架中心距之一半、同一构架所属二轮对轴距之一半。对式(18)进行位移变分，得

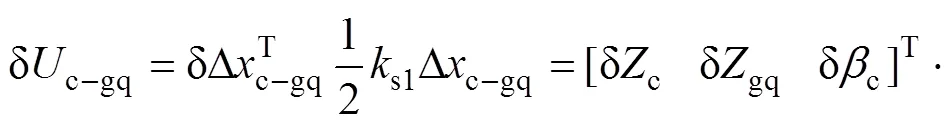
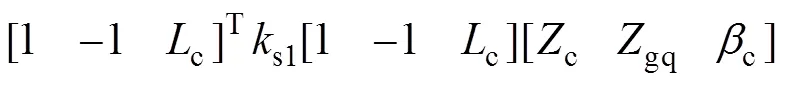
前构架与第1轮对之间的弹簧刚度矩阵和第1轮轨接触对的弹簧刚度矩阵可按类似方法获得。

仿照上述方法，根据位移参数在矩阵中的位置，可以组装车辆系统的总刚度矩阵。质量矩阵与阻尼矩阵的形成与此类似。

2.2.3 轨道系统矩阵

取2个扣件之间的轨段为轨道系统的1个有限单元，若不考虑轨道板与轨道板之间的缝隙，则无论多长的轨道系统矩阵，均可以基于此有限单元的质量、刚度、阻尼矩阵快速组装形成整个轨道系统的动力矩阵。

由于考虑轮轨之间的时变接触刚度，在整个数值积分计算过程中，车/轨系统矩阵是非线性变化的，此时，有限单元划分长度需要满足一定的精细化要求，否则将得不到正确的计算结果。

梁单元弯曲形函数采用Hermitian三次插值函数，梁单元内任意一点的竖向位移都可以通过节点的竖向位移和转角位移表示：

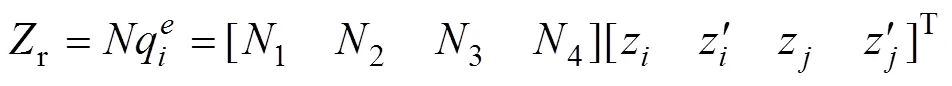
轨道系统矩阵的形成见文献[18−19]。

2.2.4 车辆系统和轨道系统的耦合

与文献[1]中每一步显示求解轮轨力的方法不同，本文的车辆系统与轨道系统的垂向耦合通过轮/轨之间的时变刚度系数分配的方法实现。通过对第1~4轮轨接触弹簧变形能的位移变分，可获得轮轨之间弹簧刚度矩阵。如第1轮轨接触对的弹性变形能变分为

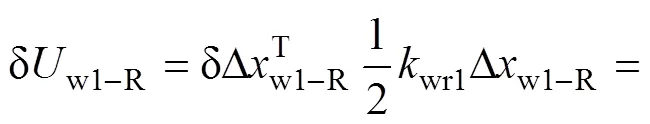
经过重分配后的第1轮轨接触刚度矩阵为

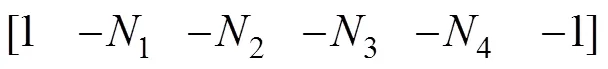
通过式(23)~(25)实现了轮对垂向振动位移、轮对所在的钢轨接触单元节点位移及轮/轨接触点的轨道不平顺等位移参数的衔接。其余3个轮/轨接触对的刚度矩阵可按类似方法获得。这样，便解决了车辆系统和轨道系统的垂向耦合问题。

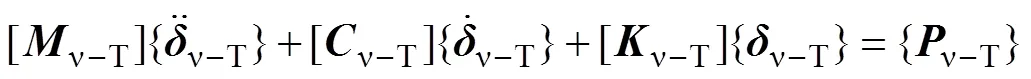
需要注意的是：式(26)并非最终的车辆−轨道耦合振动方程，因为耦合系统的刚度矩阵中含有非独立位移参数的弹性变形能，如式(17)中的后8个振动位移参数。应将轨道不平顺实测或反演值代入式(26)，形成车辆−轨道系统的内部激励，然后划去非独立矩阵方程，形成最终的耦合振动方程，其具体原理见文献[2]。本文采用wilson−法求解此振动方程，积分步长为0.05 ms。

采用较小的积分步长及轮轨密贴的方法，相当于给定了轮轨之间的约束条件，在较大的时间步长(如0.001~0.010 s)[2−3]时也能得到收敛解。而采用轮轨时变接触刚度完全模拟轮轨之间的自然接触状态，在时域数值积分时，每一积分步内所有的力素是不变的，而实际上此步长内的轮轨力是非线性变化的，时间步长越长，与实际的轮轨接触状态差别越大。通过仿真计算，认为采用轮轨时变接触刚度时，积分时间0.05 ms较合理。

3 模型验证结果与计算结果比较

3.1 脉冲型短波不平顺激励

为验证基于轮轨接触时变刚度系数的车辆−轨道耦合振动分析模型的正确性，采用与文献[18]中相同的计算条件，以长钢轨焊接区轨面短波不平顺(短波波长为0.1 m，长波和短波波幅分别为0.3 mm和0.2 mm)为轨道不平顺激励波形，见图3。跟踪计算第1轮对及其对应轨道结构的动力响应时程(如轮轨垂向作用力、钢轨加速度、轨道板加速度和钢轨位移等)，计算结果见图4。

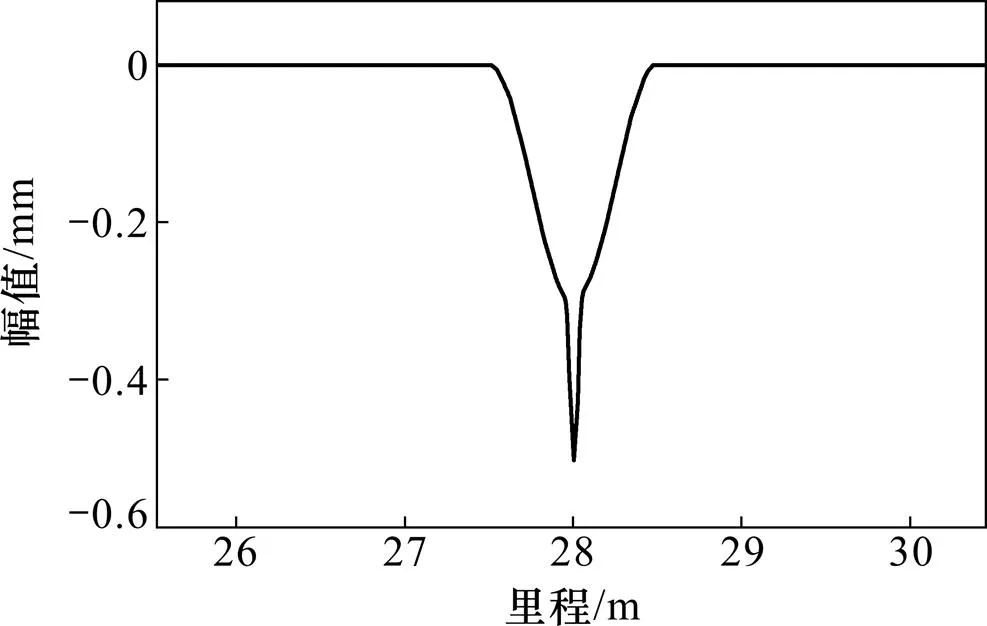
图3 钢轨焊接区轨面短波不平顺激励波形

从图4及文献[21]中计算结果可知：本文计算所获得的轮轨作用力、钢轨加速度响应波幅及钢轨位移响应波形几乎一致，但轨道板振动加速度及钢轨位移响应幅值与文献[21]中结果存在较大差别，这与本文有限元模型划分精度及积分步长有一定的关系。总的来说，本文的计算模型是正确的。

同时，比较本文模型与轮轨密贴模型的计算结果(图5，积分步长0.5 ms)可知轮轨密贴模型的计算结果与文献[21]中结果和本文模型计算结果均存在较大差异，其轮轨作用力产生的振动响应远比轮轨弹性接触模型的的振动响应大。其原因在于轮轨密贴是一种轮轨刚性接触的处理方法。同时，由式(3)~(5)所示的轮轨约束方程可知，脉冲型短波不平顺的附加速度及加速度(见图6)对轮轨之间的相互作用产生很大的影响，而实际的轮轨弹性接触状态能极大地弱化这种作用。虽然轮轨密贴模型计算结果表明存在跳轨现象，但其跳轨持续时间及响应幅值没有得到正确反映。

3.2 轨道随机不平顺中波和长波激励

这里仍然采用与3.1节中相同的系统动力参数。通过统计、归纳武广高速铁路2013年近9月的轨道高低不平顺谱，采用逆傅里叶变换方法[22]，反演获得轨道高低随机不平顺，波长范围为1~60 m，可作为中波和长波不平顺激励源，见图7。2种模型的积分时间均取为0.05 ms。

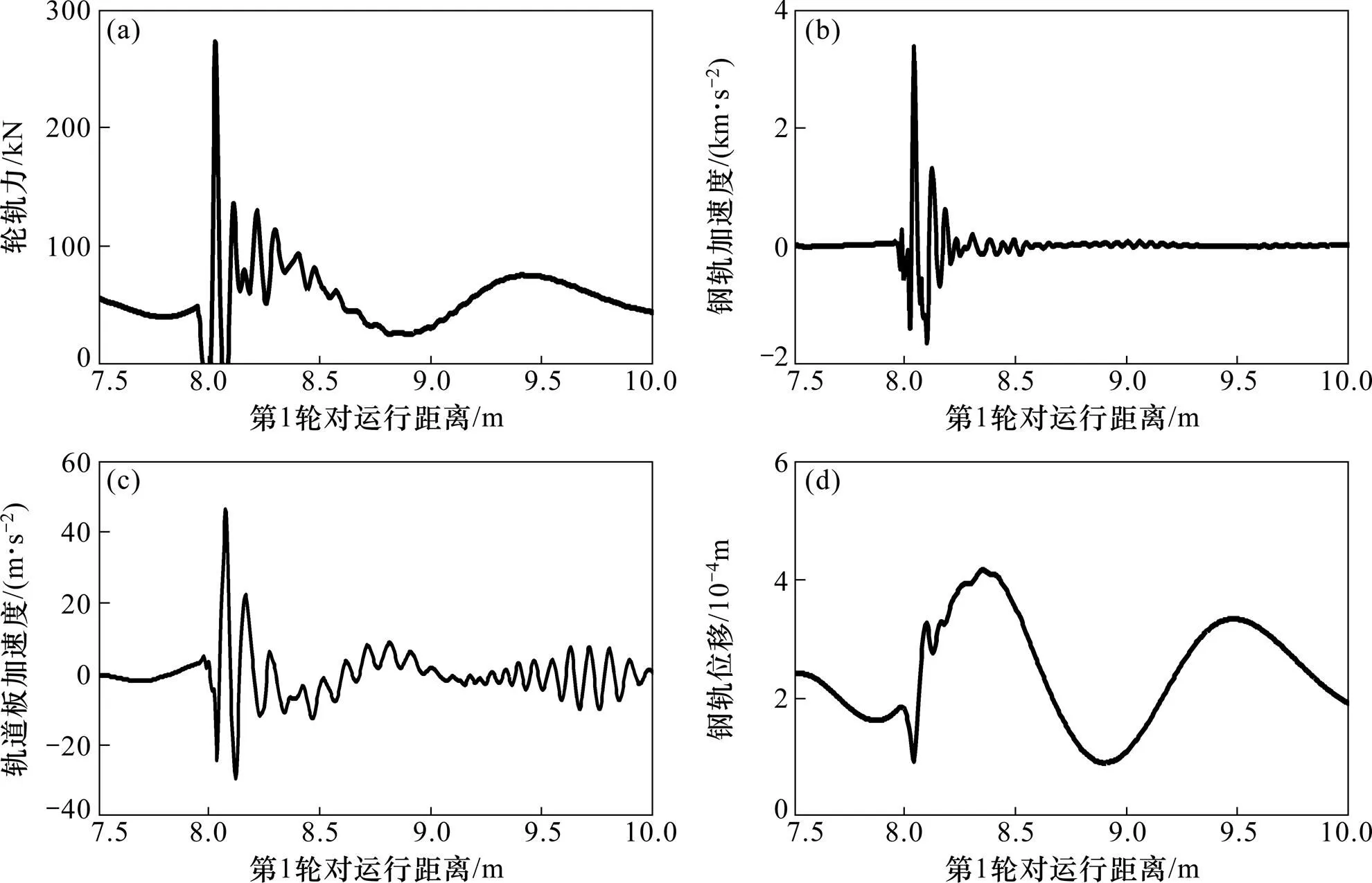
(a) 轮轨作用力响应；(b) 钢轨加速度响应；(c) 轨道板加速度响应；(d) 钢轨位移响应

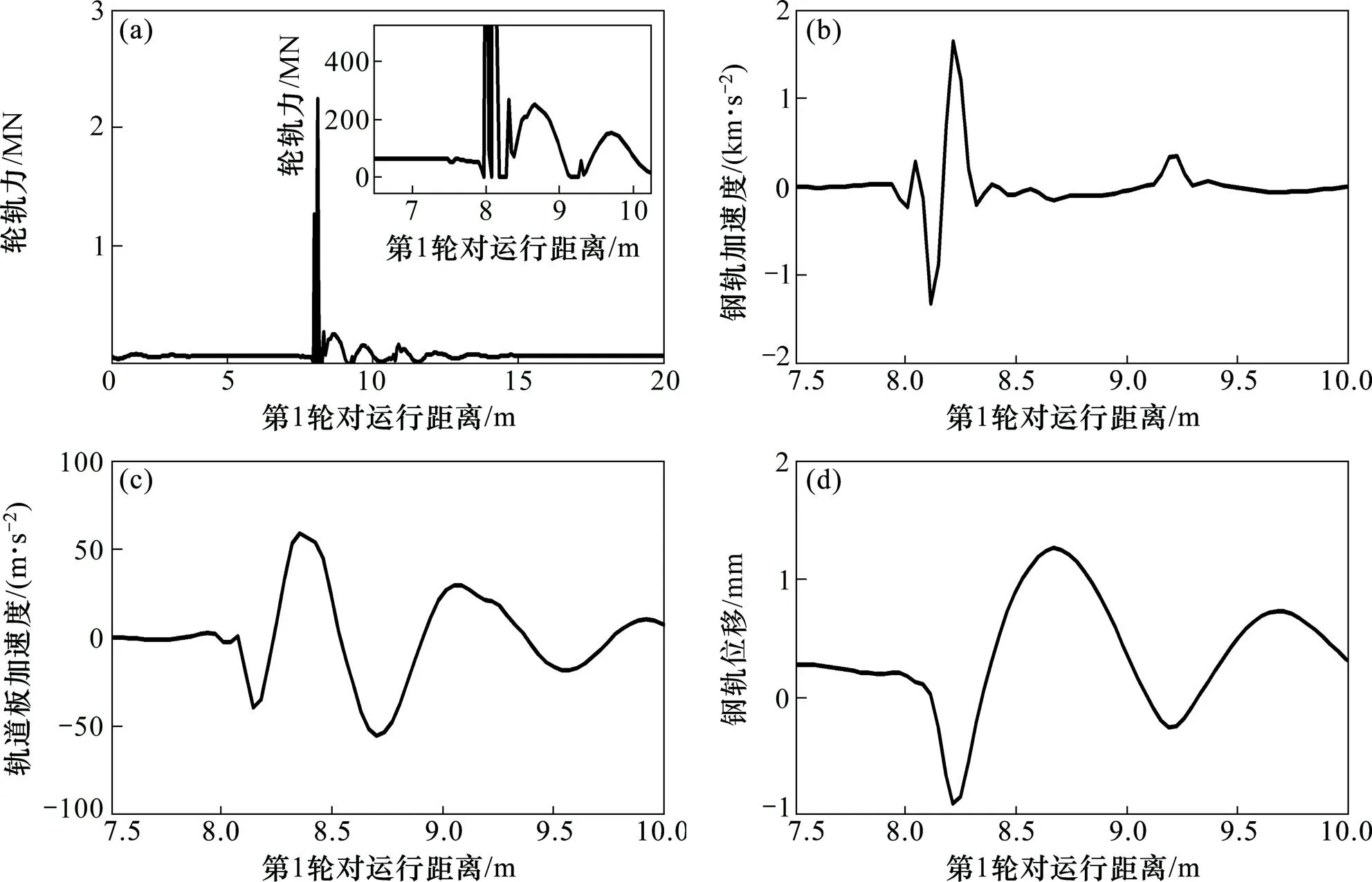
(a) 轮轨作用力响应；(b) 钢轨加速度响应；(c) 轨道板加速度响应；(d) 钢轨位移响应

图6 脉冲短波不平顺的附加加速度

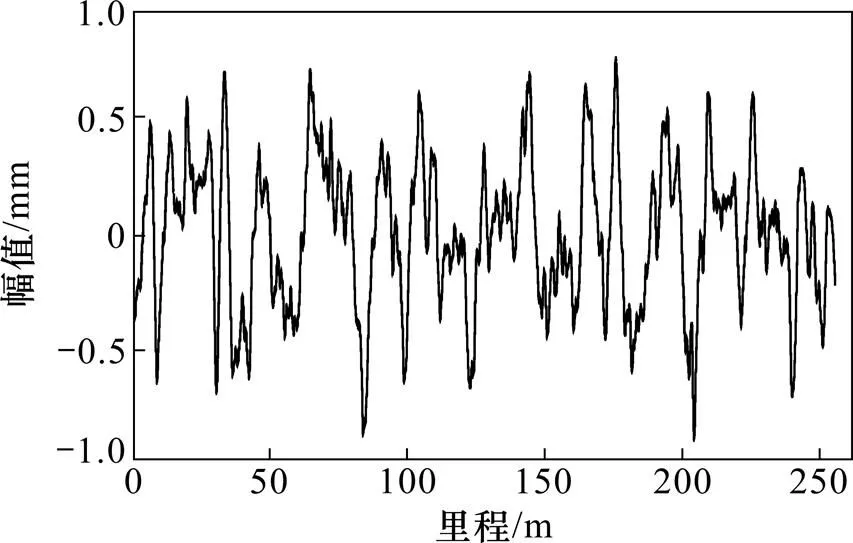
图7 轨道高低不平顺波形

3.2.1 车辆系统振动响应

车体和前构架的振动位移及振动加速度计算波形及幅值见图8。由于轮轨时变接触刚度系数模型和轮轨密贴模型对轮对位移参数的考虑完全不同，这里不进行不同车辆振动系统之间的比较。

从图8可知：2种模型在中、长波不平顺激励下产生的车辆系统振动响应基本一致。这说明在铁路线路状态较缓和、无短波高频激励时，轮轨的弹性或刚性接触对车辆系统的振动响应影响不大。

3.2.2 轨道系统振动响应

某里程处钢轨及轨道板单元中点的振动位移及加速度响应波形与幅值比较见图9。

从图9可知：2种模型获得的轨道系统计算结果相差不大。但作为轮轨系统的直接接触单元，轮轨密贴模型的钢轨位移及加速度响应比轮轨弹性接触模型的稍大。

3.2.3 轮轨力响应

轮轨力是车辆−轨道系统振动特征最显著和最直接的表达参数，这里对2种模型第1轮对的轮轨力时域及频域特征进行比较分析，见图10。

从图10可知：2种模型的频率特征分布基本一致；在轮轨力的时域分布上，轮轨时变刚度模型的轮轨力基本在轮对轴重附近波动；但由式(6)~(9)计算获得的轮轨密贴模型轮轨力的整体波动均值比轮轨时变刚度系数模型的大(这与钢轨振动响应较大的计算结果一致)，改变积分步长及运行速度，仍得到类似结果，并且运行速度越快，积分步长越短，这种差别越明显。

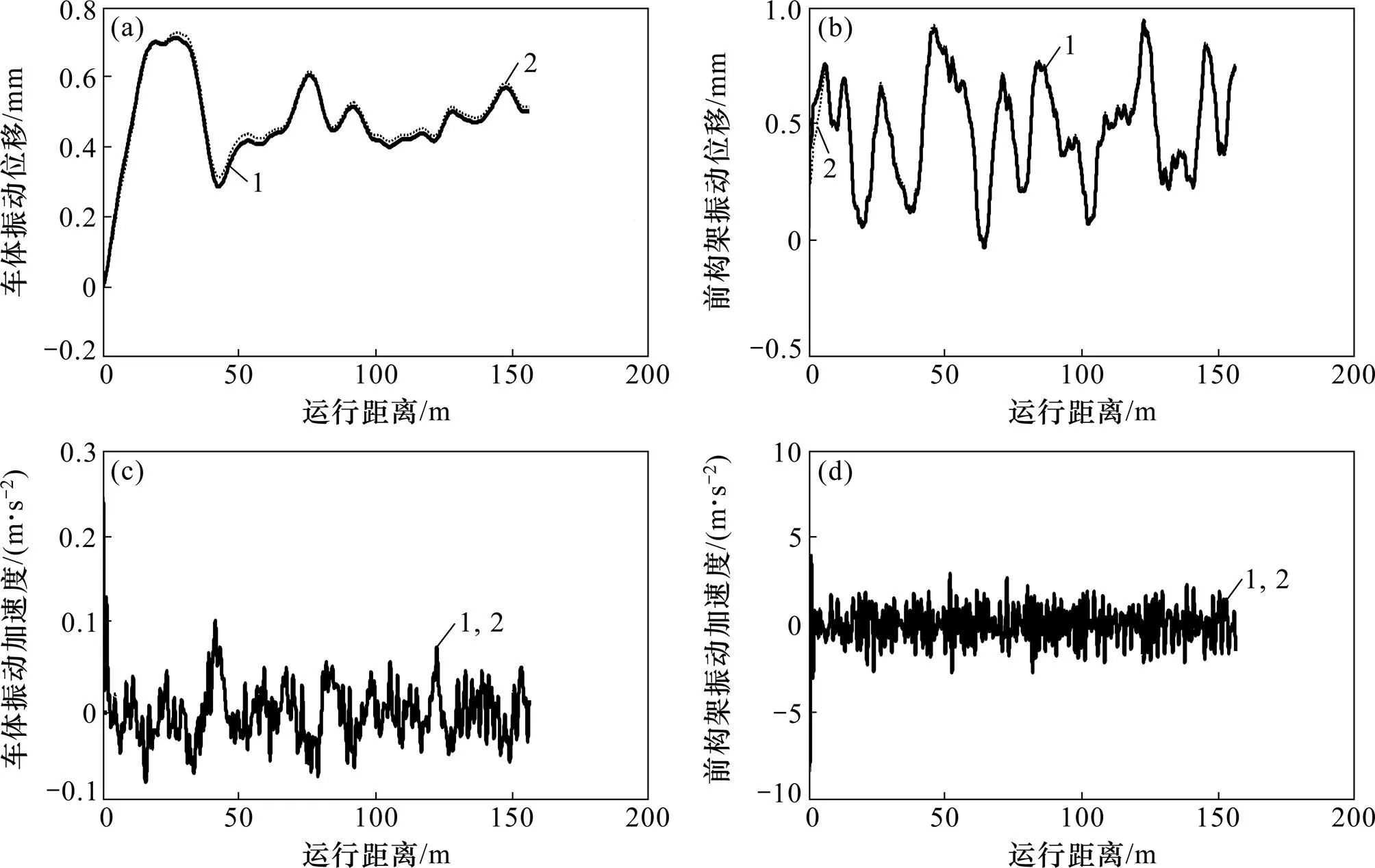
(a) 车体振动位移；(b) 前构架振动位移；(c) 车体振动加速度；(d) 前构架振动加速度

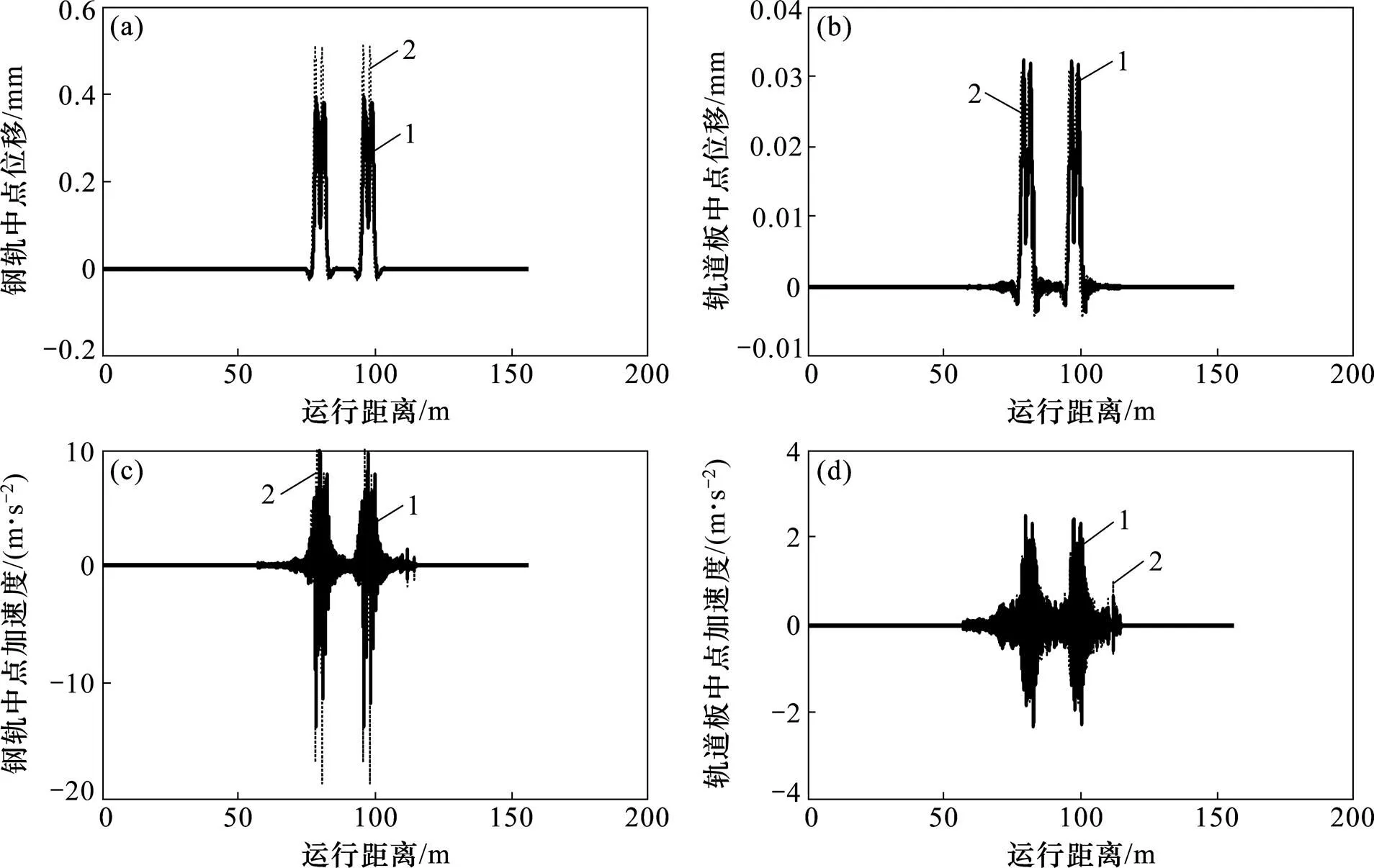
(a) 钢轨中点振动位移；(b) 轨道板振动位移；(c) 钢轨中点振动加速度；(d) 轨道板振动加速度

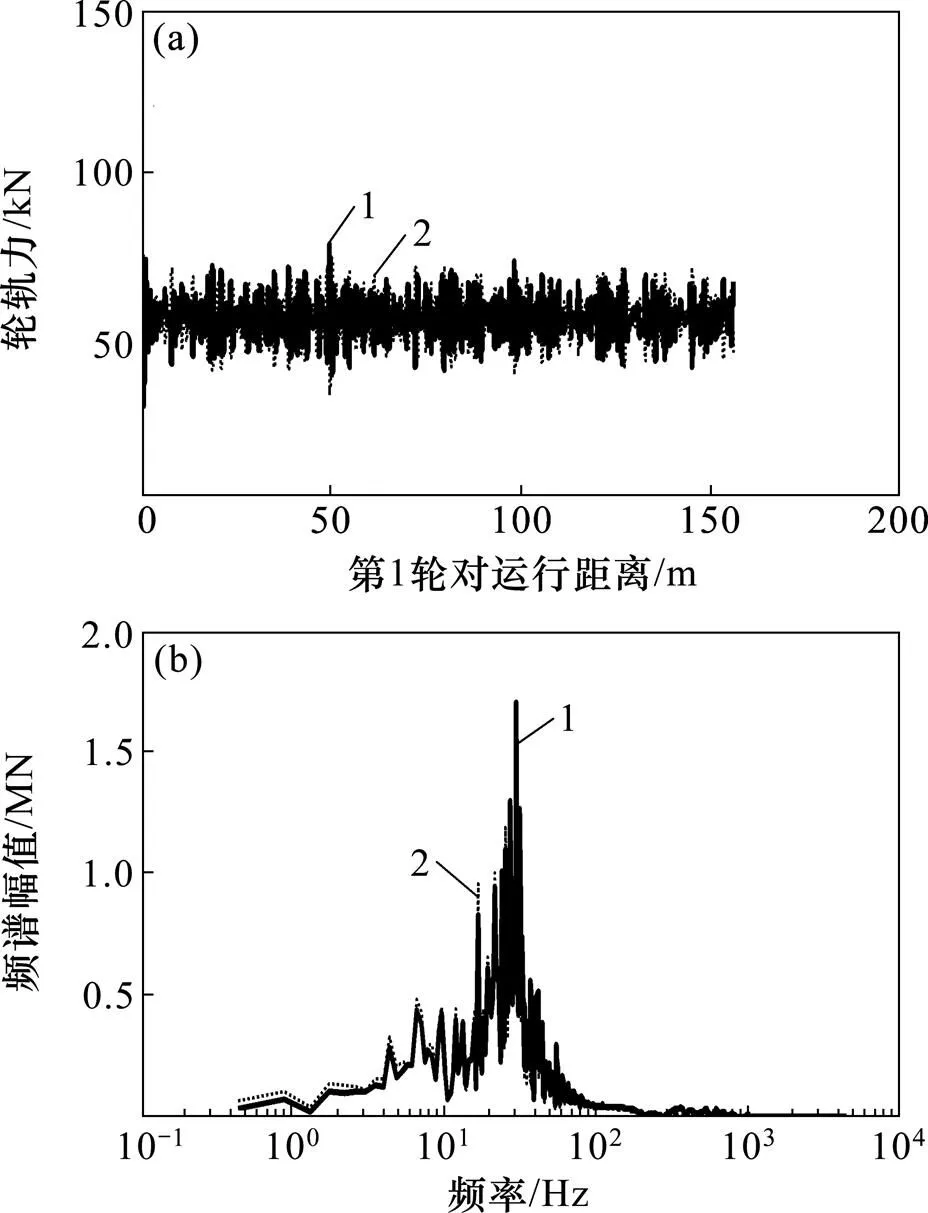
(a) 轮轨力； (b) 轮轨力频谱幅值

需要指出的是：基于达朗贝尔原理，采用式(6)~(9)计算轮轨力是正确的。本文采用轮轨时变接触刚度模型，根据每一积分步获得的车辆系统振动响应用式(6)~(9)计算相应的轮轨力，并与按赫兹接触理论计算结果进行比较，见图11。

从图11可知：基于赫兹接触理论和基于达朗贝尔原理的轮轨力计算值基本一致，由此表明式(6)~(9)用于轮轨力计算的正确性。另一方面，图11所示计算结果表明了力学原理的统一性，无论轮轨之间的相互作用多么复杂，若单独隔离车辆系统或轨道系统，则在某一瞬时，它必定处在动力平衡状态。文献[2]采用达朗贝尔原理计算的轮轴横向摇摆力与实测结果接近，说明车辆−轨道系统的垂向、横向振动均满足这一基本原理。

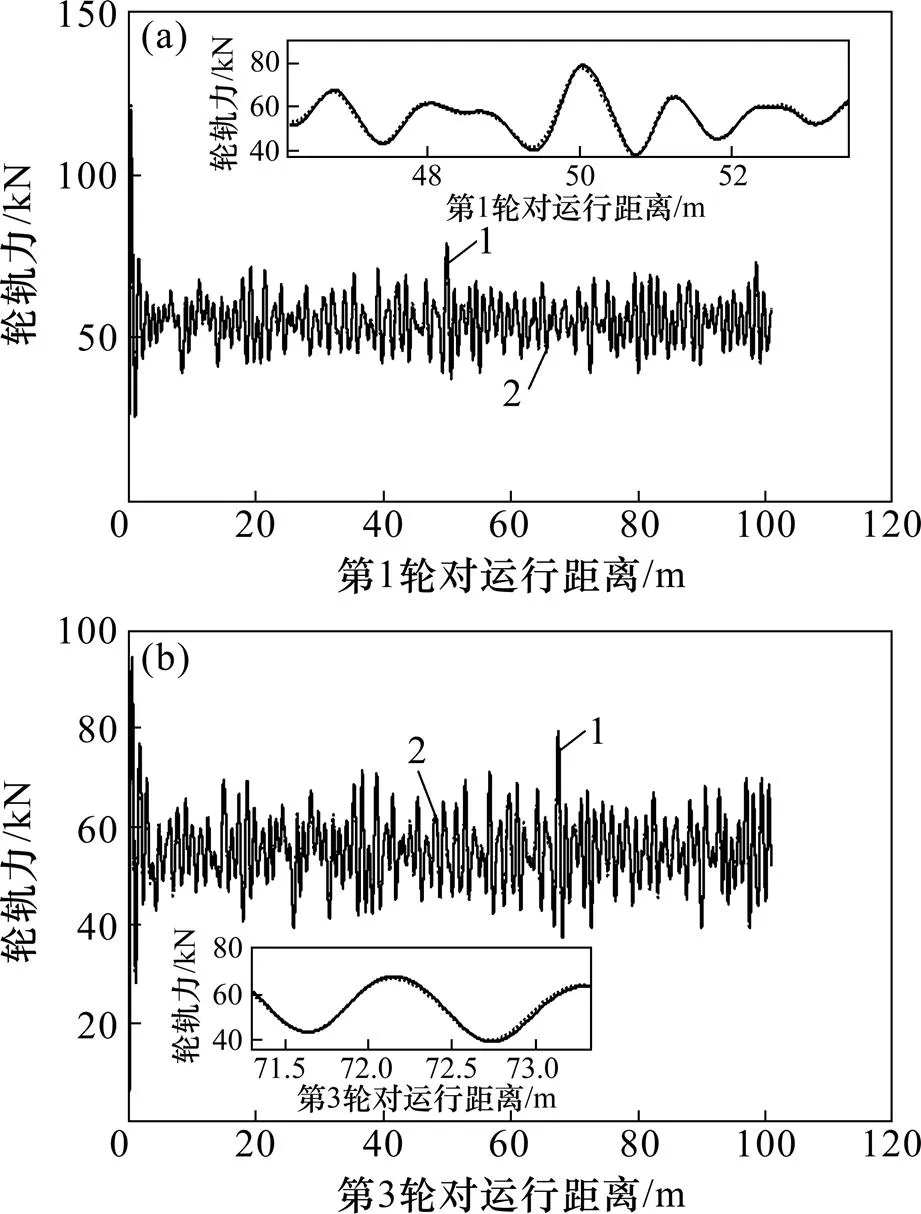
(a) 第1轮对轮轨力时程；(b) 第3轮轨轮轨力时程

4 结论

1) 对于轮轨非线性接触问题，采用“局部线性−整体非线性”的方法是可行的，解决了轮轨接触位移函数的选取问题，便于用能量变分法建立统一的车辆−轨道耦合振动方程。

2) 取轮轨相互作用力为内力，轨道(桥梁)的边界条件为车−轨(桥)系统的边界条件。将轮轨力“隐式”处理为轮轨时变接触刚度系数的动力分析方法是可行的。

3) 轮轨时变刚度模型与轮轨密贴模型在中、长波不平顺激励下，产生的系统动力响应基本一致，但当轮轨密贴模型在积分步长较小时，其刚性接触的假设将逐渐脱离轮轨实际的弹性接触状态，并且动力响应较大。

4) 轮轨密贴模型中所采用轮轨刚性接触方法不适合线路短波不平顺激励工况。

[1] 翟婉明. 车辆-轨道耦合动力学[M]. 北京: 科学出版社, 2007: 32−55. ZHAI Wanming. Vehicle and track coupling dynamics[M]. Beijing: Science Press, 2007: 32−55.

[2] 曾庆元. 列车桥梁时变系统振动分析理论与应用[M]. 北京: 中国铁道出版社, 1999: 49−56. ZENG Qingyuan. Theory of vibration analysis of train-bridge time- variant system and its applications[M]. Beijing: China Railway Press, 1999: 49−56.

[3] 娄平, 曾庆元. 车辆−轨道−桥梁系统竖向运动方程的建立[J]. 铁道学报, 2004, 26(5): 71−80. LOU Ping, ZENG Qingyuan. Formulation of equations of vertical motion for vehicle-track-bridge system[J]. Journal of the China Railway Society, 2004, 26(5): 71−80.

[4] 张敏, 张楠, 夏禾. 大跨度铁路悬索桥风−车−桥耦合动力分析[J]. 中国铁道科学, 2013, 34(4): 14−21. ZHANG Min, ZHANG Nan, XIA He. Analysis on wind-vehicle-bridge dynamic interaction for long-span railway suspension bridge[J]. China Railway Science, 2013, 34(4): 14−21.

[5] 罗震, 翟婉明, 蔡成标, 等. 车辆作用下板式轨道动力分析模型及验证[J]. 铁道学报, 2010, 32(4): 70−73. LUO Zhen, ZHAI Wanming, CAI Chengbiao, et al. Dynamics model of slab track subjected to moving vehicle and its verification[J]. Journal of the China Railway Society, 2010, 32(4): 70−73.

[6] ZHAI Wanming. Two simple fast integration methods for large-scale dynamic problems in engineering[J]. International Journal for Numerical Methods in Engineering, 1996, 39(24): 4199−4214.

[7] NEWMARK N M. A method of computation for structural dynamics[J]. Journal of the Engineering Mechanical Division, ASCE, 1959, 85(2): 67−94.

[8] 向俊, 赫丹, 曾庆元. 横向有限条与无砟轨道板单元的车轨系统竖向振动分析法[J]. 铁道学报, 2007, 29(4): 64−69. XIANG Jun, HE Dan, ZENG Qingyuan. Analysis method of vertical vibration of train and ballastless track system with the lateral finite strip and slab segment element[J]. Journal of the China Railway Society, 2007, 29(4): 64−69.

[9] 雷晓燕, 张斌, 刘庆杰. 轨道过渡段动力特性的有限元分析[J]. 中国铁道科学, 2009, 30(5): 15−21. LEI Xiaoyan, ZHANG Bin, LIU Qingjie. Finite element analysis on the dynamic characteristics of the track transition[J]. China Railway Science, 2009, 30(5): 15−21.

[10] 杨新文, 宫全美, 周顺华, 等. 高速列车作用下双块式无砟轨道与路基垂向耦合振动分析[J]. 铁道学报, 2014, 36(8): 75−83. YANG Xinwen, GONG Quanmei, ZHOU Shunhua, et al. Analysis on vertical vibration of coupled double-block ballastless track and subgrade system under high-speed train running[J]. Journal of China Railway Society, 2014, 36(8): 75−83.

[11] 杨宏印, 张海龙, 陈志军, 等. 考虑徐变影响的车-线-桥耦合有限元分析[J]. 中国铁道科学, 2013, 34(6): 13−19. YANG Hongyin, ZHANG Hailong, CHEN Zhijun, et al. Finite element analysis of train-track-bridge interaction system considering the influence of creep[J]. China Railway Science, 2013, 34(6): 13−19.

[12] CECÍLIA VALE, RUI CALÇADA. A dynamic vehicle-track interaction model for predicting the track degradation process[J]. Journal of Infrastructure Systems, 2014, 20: 1−13.

[13] 周智辉, 曾庆元. 列车-桥梁(轨道)系统振动方程解的适定性分析[J]. 力学与实践, 2005, 27(5): 46−49. ZHOU Zhihui, ZENG Qingyuan. Well-posedness of vibration equation of train-bridge (track) system[J]. Mechanics in Engineering, 2005, 27(5): 46−49.

[14] 钱伟长. 变分法及有限元[M]. 北京: 科学出版社, 1980: 26−37. QIAN Weichang. Variational methodand finite element method[M]. Beijing: Science Press, 1980: 26−37.

[15] 普齐米尼斯基. 矩阵结构分析理论[M]. 王德荣,译. 北京: 国防工业出版社, 1974: 25−36. PRZEMIENIECKI J S. Theory of matrix structural analysis[M]. WANG Derong, trans. Beijing: National Defense Industry Press, 1974: 25−36.

[16] 曾庆元. 弹性系统动力学总势能不变值原理[J]. 华中理工大学学报, 2000, 28(1): 1−3. ZENG Qingyuan. The principle of total potential energy with stationary value in elastic system dynamics[J]. Journal of Huangzhong University of Science and Technology, 2000, 28(1): 1−3.

[17] 李东平. 车辆多体系统动力学方程的有限元法[J]. 中国铁道科学, 2004, 25(5): 33−38. LI Dongping. The finite element method for establishing dynamical equations of vehicle multi-body system[J]. China Railway Science, 2004, 25(5): 33−38.

[18] 娄平, 曾庆元. 移动荷载作用下板式轨道的有限元分析[J]. 交通运输工程学报, 2004, 4(1): 29−33. LOU Ping, ZENG Qingyuan. Finite element analysis of slab track subjected to moving load[J]. Journal of Traffic and Transportation Engineering, 2004, 4(1): 29−33.

[19] 赵怀耘, 刘建新, 翟婉明. 板式轨道动力响应分析方法[J]. 交通运输工程学报, 2007, 7(5): 19−23. ZHAO Huaiyun, LIU Jianxin, ZHAI Wanming. Analysis method of dynamic responses on slab track[J]. Journal of Traffic and Transportation, 2007, 7(5): 19−23.

[20] 曾庆元, 杨平. 形成矩阵的“对号入座”法则与桁梁空间分析的桁段单元法[J]. 铁道学报, 1986, 8(2): 48−59. ZENG Qingyuan, YANG Ping. The “set-in-right-position” rule for forming structural matrices and the finite truss-element method for space analysis of truss bridges[J]. Journal of the China Railway Society, 1986, 8(2): 48−59.

[21] 翟婉明, 韩卫军, 蔡成标, 等. 高速铁路板式轨道动力特性研究[J]. 铁道学报, 1999, 21(6): 65−69. ZHAI Wanming, HAN Weijun, CAI Chengbiao, et al. Dynamic properties of high-speed railway slab tracks[J]. Journal of the China Railway Science, 1999, 21(6): 65−69.

[22] 陈果, 翟婉明. 铁路轨道不平顺随机过程的数值模拟[J]. 西南交通大学学报, 1999, 34(2): 138−142. CHEN Guo, ZHAI Wanming. Numerical simulation of the stochastic process of railway track irregularities[J]. Journal of Southwest Jiaotong University, 1999, 34(2): 138−142.

(编辑 陈灿华)

Vehicle-track system vertical vibration analysis based on wheel-railtime-varying contact stiffness

HE Tianlong1, 2, CHEN Xianmai1, 2, XU Lei3

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;3. Track Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China)

A vertical and unified equation of the vehicle-track system was established with finite element theory and energy variation method, and wheel-rail time-varying contact stiffness replaced wheel-track nonlinear contact force on dynamic effects to simulate the natural contact between wheel and rail. The validity of the model was verified by inputting the long and medium-wave irregularity of track and pulsed shortwave in this model and the dynamic response was calculated. The tight contact model between wheel and rail, which was popular in China was compared and analyzed.The results show that analyzing dynamic response of the vehicle-track system at the tight contact model for the long and medium-wave irregularity of track is feasible. However, the rigid method between wheel and track will amplify the incentive effect of shortwave for the shortwave irregularity of track, the treatment method about jumping rail should be improved.

vehicle-track coupling system; time-varying contact stiffness; vertical vibration; energy variation method; unified equation

10.11817/j.issn.1672−7207.2017.08.023

U213.2；U211.5

A

1672−7207(2017)08−2142−10

2016−08−23；

2016−10−22

国家自然科学基金资助项目(51478482)；中国铁路总公司科技研究开发计划项目(Z2013-G006)；武汉铁路局科技发展计划项目(13G04)(Project(51478482) supported by the National Natural Science Foundation of China; Project(Z2013-G006) supported by the Science and Technology Research and Development of China Railway Corporation; Project(13G04) supported by the Science and Technology Development Plan of Wuhan Railway Administration)

陈宪麦，副教授，从事轨道动力学、线路评估及养护维修等研究；E-mail：xianmaichen@aliyun.com