减振型双块式的无砟轨道声振特性

王根平，李成辉，陈代秀，段海滨

减振型双块式的无砟轨道声振特性

王根平，李成辉，陈代秀，段海滨

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都，610031)

为研究减振型双块式振动衰减以及声辐射频域特性，基于FEM/BEM方法，建立轨道系统的振动力学模型和声学边界元模型。研究结果表明：轨下胶垫的减振优势主要体现在200~2 500 Hz频域范围内，减振层的减振优势主要体现在50~3 750 Hz频域范围内；在轨道结构系统中，钢轨声贡献率随频率增大而增大，低频时，轨道系统其他结构层的声辐射不容忽视；轨道系统各结构层的声辐射效率特征较复杂，均表现为开始在一频域范围内上升，而后趋于平稳震荡，钢轨声辐射效率变化速率明显比其他结构层的小；在125 Hz以下，钢轨轨腰声贡献率明显比轨头和轨底的大，而后随频率增加，轨底声贡献率比轨腰和轨头的大；本文预测的振动噪声与其他模型得出的结果有很好的一致性。

减振型双块式；有限元法；边界元法；振动衰减；声辐射

随着人们对环境要求的提高，铁路振动噪声问题已经被越来越多的研究者所关注。轨道结构噪声辐射与其振动密不可分[1]。减振型双块式无砟轨道是一种减振性能较好的无砟轨道结构型式，由钢轨、轨下胶垫(扣件系统)、轨枕、道床板、减振层、支承层(路基地段)或底座(桥梁地段)等组成，曾在郑西(郑州—西安)客运专线新渭南高架站上使用，综合减振可达12 dB[2]，其应用前景广阔。为分析减振型双块式轨道结构的振动衰减以及各结构层声辐射频域特性，需建立合理的轨道结构振动−声辐射计算模型。对于轨道结构振动声辐射问题，提出了许多模型。如REMINGTON等[3−6]均从轮轨相互作用角度出发，建立了轮轨滚动噪声预测模型。但这些模型中只考虑了与车轮直接接触的钢轨，利用钢轨振动声辐射效率和钢轨振动响应预测其声辐射。为体现轨道下部结构对振动噪声的影响，JONES等[7]对REMINGTON模型进行了改进，轨道模型扩展成由钢轨、垫层、及轨下基础组成，计算结果得到了现场测试验证，这也说明轨下结构对轮轨噪声的影响不容忽视。后来，VINCENT等[8−9]就轨道参数对轮轨滚动噪声影响进行了研究；WU等[10−12]研究了钢轨垂向振动声辐射特性；杨新文等[13]根据虚功原理和哈密尔顿原理建立了轨道板的振动方程，以轨道板的振动响应作为边界条件计算轨道板的声辐射；方锐等[14−15]对只考虑钢轨和轨枕的轨道结构在不同轨道参数下的振动声辐射特性进行了研究；刘林芽等[16−17]结合有限元和边界元法研究了钢轨和轨道板的高频振动以及声辐射特性。现有对轨道结构振动声辐射的研究中，都对轨道结构模型进行了简化，但并没有从整体角度研究轨道系统振动声辐射特性。减振型双块式无砟轨道具有很好的层状减振性能，为了解其振动衰减以及声辐射特性，本文基于FEM/BEM方法，建立轨道系统垂向振动−声辐射计算模型，研究单位垂向简谐激励作用下的轨道系统振动传递和声辐射特性，以便为低振动噪声轨道的设计提供依据与参考。

1 轨道结构振动声辐射分析理论

轨道结构是一种复杂的工程结构物，采用解析方法很难求取复杂结构振动声辐射特性参数。有限元方法和边界元方法成为研究三维复杂结构在外力作用下的稳态声辐射特性和声振耦合机理的有效方法。

1.1 结构−有限元理论

轨道结构的刚度和流体(空气)的刚度相差很大，不考虑流固界面的耦合作用，在简谐激励作用下，轨道结构的运动方程为

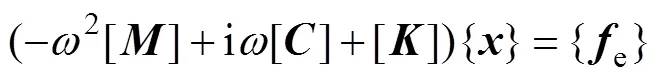
式中：[]，[]和[]分别为质量矩阵、刚度矩阵和阻尼矩阵；{e}为外激励荷载向量；{}为节点位移向量；为激励频率。

1.2 声学−边界限元理论

在简谐荷载作用下结构表面振动会扰动外部流体介质，流体场中辐射声压(，)需满足Helmholtz方程：

求解式(2)需结合具体声源和具体边界条件。

流固界面边界条件为

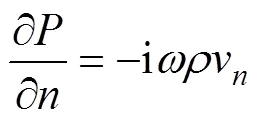
Sommerfeld辐射条件为

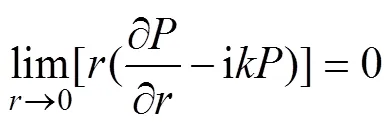
利用格林函数可以将方程(2)转化成Rayleigh积分：

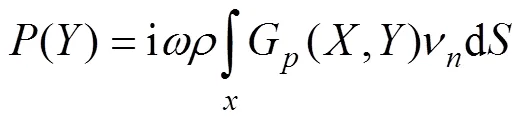
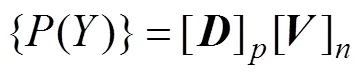
式中：[]为系数矩阵；[]为结构表面各点振动法线速度向量；()为声场中某一点声压。

当在结构表面上时，根据式(5)求得结构表面上各点声压，并由结构的振动响应得到结构表面的法向速度，可求得轮轨系统结构的辐射声功率：

声辐射效率反映相同振动幅度的结构部件辐射声功率能力。而结构的辐射声功率与结构的辐射表面面积、辐射效率和表面均方速度有关，表达式为

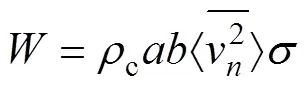
结构辐射效率的表达式为

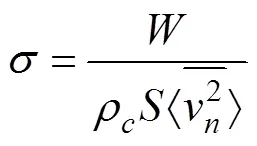
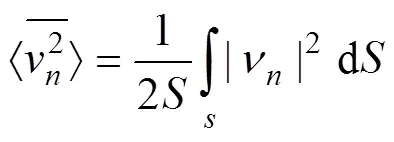
2 轨道结构振动声辐射计算模型

2.1 轨道结构振动计算模型

由于只研究轨道结构系统在垂向力作用下的声振特性，不考虑轮轨耦合作用，由文献[18]可知：当轨道结构系统上有一作用力时，由于轨道结构系统阻尼的作用，该作用力影响最强烈的区域是激振点前、后各三跨轨枕范围，因此，为提高计算效率，在满足工程精度时考虑10根跨枕。钢轨的截面尺寸按60 kg/m轨选取，轨枕长×宽×高为0.78 m×0.30 m×0.04 m；道床板长×宽×高为5.90 m×2.80 m×0.26 m；底座板长×宽×高为5.90 m×2.80 m×0.21 m；轨枕间距0.60 m。减振型双块式轨道结构力学模型如图1所示。

(a)轨道结构力学模型横向；(b)轨道结构力学模型纵向

模型中考虑钢轨、轨下胶垫(扣件系统)、轨枕、道床板、减振层和底座板(桥梁)。为计算轨道结构声辐射奠定基础，钢轨、轨枕、道床板和底座板均采用8节点六面体单元离散。考虑到声辐射计算时对单元尺寸的要求，在对结构进行离散时，单元尺寸设置为0.01 m。轨下胶垫和减振层均采用线弹性弹簧阻尼单元离散。

激励源采用单位简谐荷载，单位简谐荷载是一种形式较简单的反复荷载，更容易考虑荷载频率变化对结构动力响应的影响，是计算结构导纳特性最简单有效的荷载方式，加载点选在轨道结构中间的钢轨顶部。

为减小计算量，选取一半轨道结构，在轨道中心处设对称边界条件。同时根据THOMPSON[19]提出的钢轨中波传播计算模型，为消除钢轨端部振动波反射对高频振动特性的影响，在钢轨两端设对称边界条件。因底座板底部和桥梁梁面直接连接，桥梁梁面刚性很大，故可将底座板底部全约束。

2.2 轨道结构声辐射计算模型

在建立轨道结构声辐射计算模型时，基于边界元理论，只需要对结构表面划分单元。需注意的是：利用有限元法求得的结构表面振动响应将会作为声辐射计算的边界条件，所以，结构声学边界元网格和有限元网格长×宽不能相差太大，否则不能得到很好的计算结果。要求最大单元长×宽小于最高频率点处波长的1/6[20]，本文边界元网格长×宽和有限元网格长×宽一致。声辐射边界元模型如图2所示。

为了解轨道系统的声辐射特性，在轨道系统附近位置建立1个面场点和1个点场点。其中面场点平行于轨道系统纵向，距离轨道系统边缘中心线2.0 m，长度为5.9 m，高度为1.0 m。所示点场点是位于面场点的1个特殊点(与整个轨道结构中心对齐)，具体见图2。

(a) 空气场中面场点；(b) 轨道结构表面形成的边界元模型

3 数值计算结果与讨论

减振型双块式无砟轨道结构的材料参数见表1，计算频率范围为50~5 000 Hz。

3.1 振动结果与讨论

采用完全法计算荷载作用下的轨道系统导纳。为研究振动传递特性，选取hg0，hg1，hg2，hg3和hg4共5个点研究振动在钢轨中纵向传递，选取hg0，gz0，hb0和hd0共4个点研究振动在轨道系统中垂向传递。具体拾振点布置如图3所示。

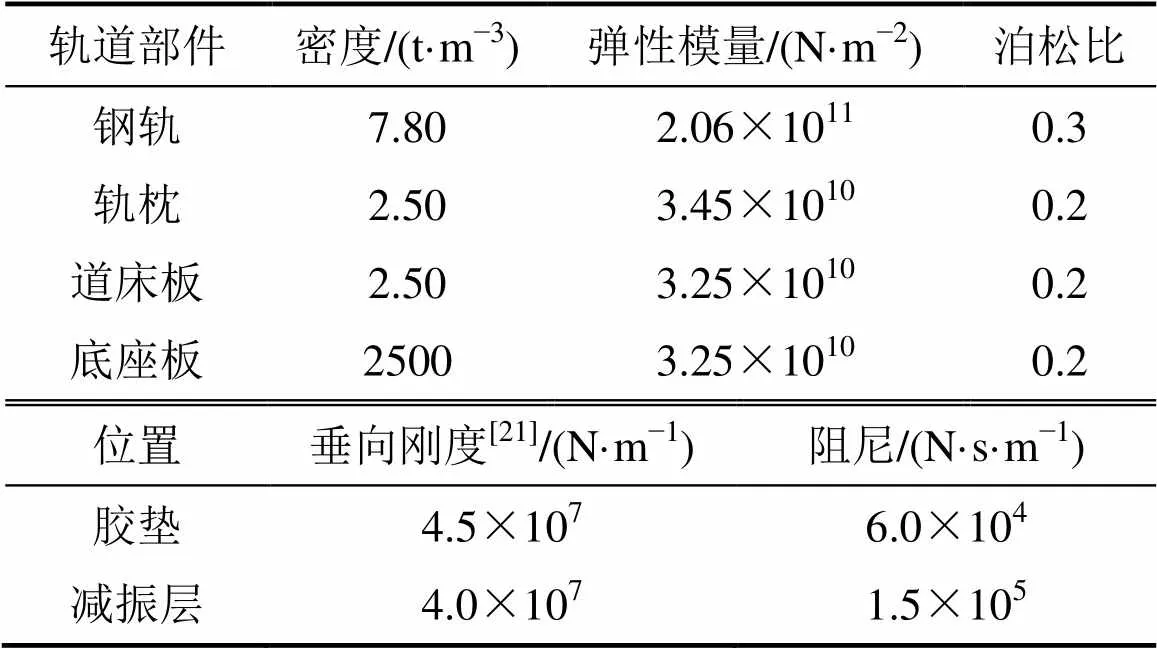
表1 减振双块式轨道结构材料参数

图3 激励与拾振点布置

3.1.1 振动纵向传递

声辐射与结构表面的振动速度有关，故提取轨道系统各拾振点的表面振动速度。钢轨纵向拾振点速度导纳见图4。从图4可知：振动在钢轨中纵向传递时，短距离内的传递衰减特性并不明显。这是因为振动是以纵向机械波的形式在钢轨中传递，频率越高，波长越小，振动的能量越大，一致性就越强。

3.1.2 振动垂向传递

图5所示为振动垂向传递的各拾振点速度导纳幅值。从图5可知：当频率为50~200 Hz时，钢轨、轨枕和轨道板的速度导纳幅值没有出现较大差别，轨下胶垫并没有体现出它的减振性能；当频率为200~2 500 Hz时，钢轨到轨枕的振动传递呈数量级衰减；当频率为2 500~5 000 Hz时，振动衰减能力又开始减弱。这说明轨下胶垫的减振优势主要体现在中频，低频和高频都不能有效地削弱振动由钢轨向轨下基础传递；由于减振层存在，使得在50~3 750 Hz范围内振动传递到底座板时衰减特别大；在3 750~5 000 Hz内衰减能力减弱，说明减振层的减振优势主要体现在中、低频。

1—hg0；2—hg1；3—hg2；4—hg3；5—hg4。

1—hg0；2—gz0；3—hb0；4—hd0。

3.2 声辐射结果与讨论

计算中取空气密度=1.21 kg/m3，空气中声速=340 m/s。对减振双块式轨道各结构层声压级和声辐射效率进行研究。

3.2.1 轨道系统各结构层声压级

由于人耳能听到的声音范围比较大，用声压的绝对值来衡量声音幅度很不方便，故采用声压级衡量声压，其参考声压为2×10−5Pa。同时，为使得声音与人耳听觉感受一致，使用A计权声级对噪声进行主观评价。本文计算得到的轨道系统各结构层场点声压如图6所示。

从图6可知：轨道各结构层的声辐射频域特性相当复杂，声辐射随频率变化过程中出现多次波峰和波谷，这与图5中的振动变化过程中的波峰和波谷相对应，在2 kHz左右钢轨的声辐射出现了最大值；整体来讲，钢轨的声贡献比例随频率增加而变大，其他结构层声贡献比例随频率变大而减少；钢轨噪声贡献主要体现在高频。低频时，轨道其他结构层声辐射也占有很大比例；50~120 Hz前轨道板噪声比钢轨的噪声大，这与声辐射面积有关。

3.2.2 轨道系统各结构层声辐射效率

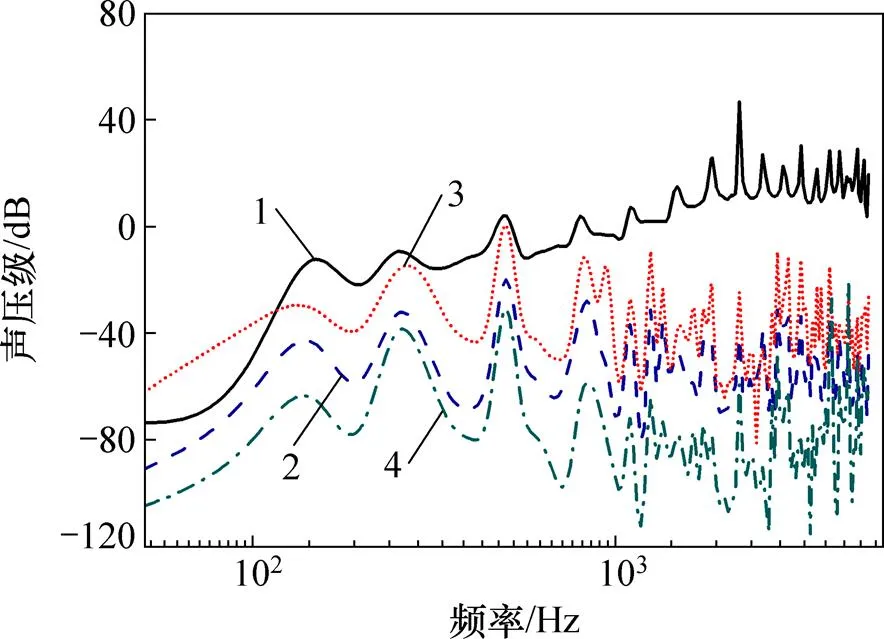
1—钢轨；2—轨枕；3—轨道板；4—底座板。

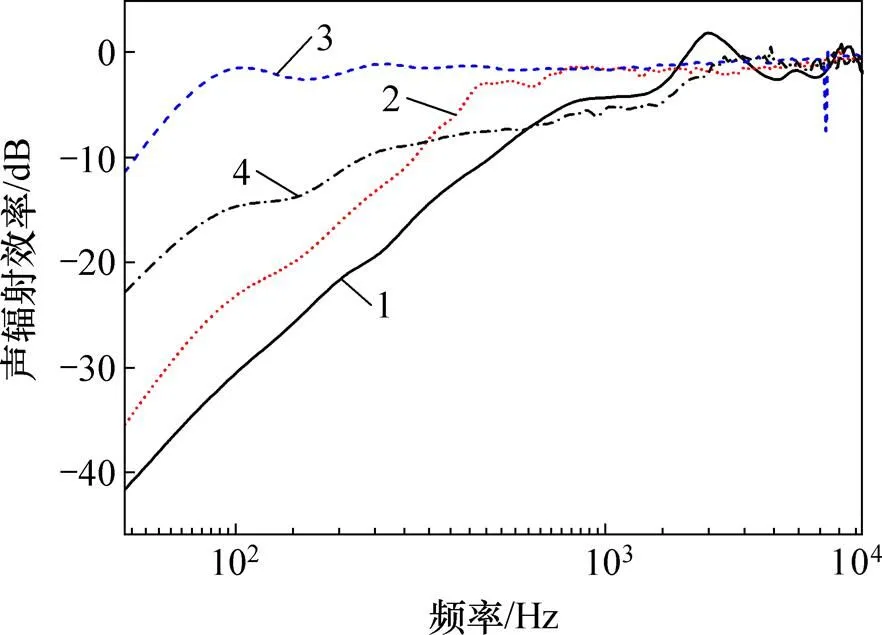
1—钢轨；2—轨枕；3—轨道板；4—底座板。

从图7得知：轨道系统各结构层的声辐射效率特征较复杂，整体表现为开始在一频域范围内上升变化，而后趋于平稳震荡。

钢轨是轨道结构发声的主要部位，在钢轨声辐射效率随频率上升过程中，其变化明显比其他结构层的变化小，在50~800 Hz范围内钢轨声辐射效率基本呈线性变化，在2 000 Hz左右有1个明显波峰，在4 700 Hz左右也出现1个峰值，但峰值比2 000 Hz处的峰值略小，这与文献[11]中结果一致，说明在2 000 Hz和4 700 Hz左右钢轨振动引起的声辐射效率很高，若需对钢轨采取降噪措施，则需要对这2个频率予以考虑。轨枕声辐射效率的变化趋势大致与NIELSEN 等[8−9]得出的变化趋势相同，低频时，声辐射效率很低，高频时，轨枕声辐射效率近似为1。轨道板是轨道结构发声的重要部位，其声辐射效率在轨道系统中随频率变化最快；在约100 Hz处，声辐射效率近似达到1，这与结构表面振动速度和声辐射面积有关。底座板辐射声功率的能力最弱，这是由于减振双块式轨道减振层的作用，使得振动向下传递时，能量衰减很快。

3.2.3 钢轨板块声贡献分析

钢轨作为轨道结构声辐射的主要部分，有必要研究清楚钢轨各部位的噪声贡献。将钢轨分轨头、轨腰和轨底3个板块，计算得到的各板块噪声贡献如图8所示。

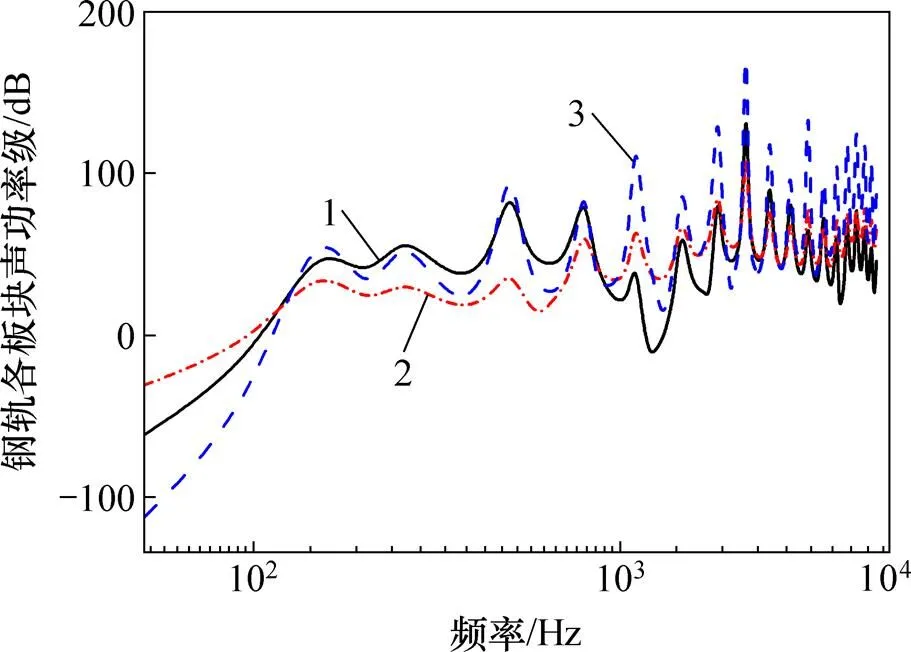
1—轨头；2—轨腰；3—轨底。

从图8可知：在垂向振动分析中，在125 Hz以下，钢轨轨腰声贡献明显比轨头和轨底的贡献大，而后轨底声贡献基本上要比轨腰和轨头的贡献大，这与振动速度法线方向和辐射面积有关。在垂向荷载激励下，轨底表面的振动速度法线方向和荷载激励方向一致，轨腰表面振动速度法线方向和荷载激励方向呈90° 夹角。

4 结论

1) 从轨道结构整体的角度计算无砟轨道结构振动声辐射，为预测轨道结构振动噪声、降低噪声轨道的设计、减小铁路轨道振动和噪音提供依据。

2) 从振动特性而言，由于轨下胶垫和减振层存在，减振双块式无砟轨道结构具有很好的减振性能；垂向传递时，轨下胶垫的减振优势主要体现在中频，减振层的减振优势主要体现在中低频；在进行轨道结构减振设计时，可合理设置轨垫和减振层参数，以便在期望的频率范围内达到减振目的。

3) 从声辐射特性而言，钢轨的声贡献主要体现在高频，频率越高，传递到下部结构层的能量越少，下部结构层声贡献比例就会减少；低频时，轨道其他结构层的声贡献不容忽视。在125 Hz以下时，钢轨轨腰声贡献明显大于轨头和轨底的贡献，而后轨底声贡献基本上大于轨腰和轨头的贡献。

[1] 雷晓燕, 圣小珍. 铁路交通噪声与振动[M]. 北京: 科学出版社, 2004: 1−10. LEI Xiaoyan, SHENG Xiaozhen. Railway traffic vibration and noise[M]. Beijing: Science Press, 2004: 1−10.

密度、施氮、施磷、施钾4个因素对产量产生一定影响，且产量随各因素的提高呈开口朝下的抛物线，存在产量最高点，各抛物线的顶点就是各单因子的最高产量，对应的是各因子的最优投入量。在试验设计范围内，当密度为123 750株/hm2时，产量为2 153.5kg/hm2；施N为52.5 kg/hm2时，产量为2 159.2 kg/hm2；施P2O5为52.5 kg/hm2时，产量为2 155.1 kg/hm2；施K2O为58.5 kg/hm2时，产量为2 163.7 kg/hm2。

[2] 刘巍, 魏周春, 畅德师, 等. 郑西客运专线新渭南高架站减振型双块式无砟轨道方案研究[J]. 铁道标准设计, 2009(5): 11−14.LIU Wei, WEI Zhouchun, CHANG Deshi, et al. Scheme on vibration reducing double block ballastless at weinan elevated station on Zhengzhou—Xi’an passenger dedicated line[J]. Railway Standard Design, 2009(5): 11−14.

[3] REMINGTON P J. Wheel/rail rolling noise I: theoretical analysis[J]. Journal of the Acoustical Society of America, 1987, 81(6): 1805−1823.

[4] REMINGTON P J. Wheel/rail rolling noise II:validation of the theory[J]. Journal of the acoustical Society of Americal, 1987, 81(6): 1824−1832.

[5] THOMPSON D J. Wheel/rail noise generation. Part I: introduction and interaction model[J]. Journal of Sound and Vibration, 1993, 161(3): 387−400.

[6] THOMPSON D J. Wheel/rail noise generation. Part III: rail vibration[J]. Journal of Sound and Vibration, 1993, 161(3): 421−447.

[7] JONES C J C, THOMPSON D J. Extended validation of a theoretical model for the TWINS prediction program for rolling noise. Part II: results[J]. Journal of Sound and Vibration, 1996, 193: 137−147.

[8] VINCENT N, BOUVET P, THOMPSON D J, et al. Theoretical optimization of track components to reduce rolling noise[J]. Journal of Sound and Vibration, 1996, 193: 161−171.

[9] NIELSEN J C O. Acoustic optimization of railway sleeper[J]. Journal of Sound and Vibration, 2000, 231(3): 753−764.

[10] WU T X, THOMPSON D J. A hybrid model for the noise generation due to railway wheel flats[J]. Journal of Sound and Vibration, 2002, 252(1): 115−139.

[11] 魏伟, 聂春戈. 钢轨声辐射特性的数值计算方法[J]. 铁道学报, 2006, 28(5): 78−82. WEI Wei, NIE Chunge. The prediction of acoustics radiation characteristics of rails by boundary element method[J]. Journal of the China Railway Society, 2006, 28(5): 78−82.

[12] 万淑敏, 吴天行. 铁路钢轨垂向振动的声辐射分析[J]. 噪声与振动控制, 2009, 29(3): 86−89. WAN Shumin, WU Tianxing. Analysis of rail acoustic radiation due to vertical vibration[J]. Noise and Vibration Control, 2009, 29(3): 86−89.

[13] 杨新文, 翟婉明, 和振兴. 轨道板声辐射特性[J]. 中国铁道科学, 2009, 30(1): 25−27. YANG Xinwen, ZHAI Wanming, HE Zhenxing. Acoustic radiation properties of railway slab[J]. China Railway Science, 2009, 30(1): 25−27.

[14] 方锐, 肖新标, 房建英, 等. 轨道结构参数对钢轨和轨枕振动特性的影响[J]. 铁道学报, 2011, 33(3): 72−76. FANG Rui, XIAO Xinbiao, FANG Jianying, et al. Effect of structure parameters of railway trackon dynamic behavior of rail and sleeper[J]. Journal of The China Railway Society, 2011, 33(3): 72−76.

[15] 方锐, 肖新标, 房建英, 等. 轨道结构参数对其声辐射特性影响[J]. 铁道学报, 2011, 33(5): 78−83. FANG Rui, XIAO Xinbiao, FANG Jianying, et al. Influence of track structure parameters on acoustic radiation[J]. Journal of the China Railway Society, 2011, 33(5): 78−83.

[16] 刘林芽, 吕锐, 刘海龙. 无砟轨道垂向高频振动响应分析[J]. 铁道科学与工程学报, 2011, 8(6): 1−6. LIU Linya, LÜ Rui, LIU Hailong. Vertical high frequency vibration response analysis of ballastless track[J]. Journal of Railway Science and Engineering, 2011, 8(6): 1−6.

[17] 刘林芽, 吕锐, 许群峰, 等. 基于有限元−边界元无砟轨道声辐射特性分析[J]. 铁道科学与工程学报, 2013, 10(1): 3−5. LIU Linya, LÜ Rui, XU Qunfeng, et al. Analysis of acoustic radiation characteristics for unballasted track based on finite element-boundary element method[J]. Journal of Railway Science and Engineering, 2013, 10(1): 3−5.

[18] 翟婉明. 车辆−轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007: 192−195. ZHAI Wanming. Vehicle-track coupling dynamics[M]. 3th ed. Beijing: Science Press, 2007: 192−195.

[19] THOMPSON D J. Experimental analysis of wave propagation in railway tracks[J]. Journal of Sound and Vibration, 1997, 203(5): 867−888.

[20] 詹福良, 徐俊伟. Virtual lab Acoustics 声学仿真计算从入门到精通[M]. 西安: 西北工业大学出版社, 2013: 5−8. ZHAN Fuliang, XUN Junwei. Virtual lab acoustics simulation calculation from grammer to proficiency[M]. Xi’an: Northwestern Polytechnical University Press, 2013: 5−8.

[21] 徐锡江. 减振型双块式无砟轨道合理刚度匹配研究[J]. 路基工程, 2013(3): 49−53. XU Xijiang. Study on reasonable stiffness matching for vibration-reduction double-block ballastless track[J]. Subgrade Engineering, 2013(3): 49−53.

(编辑 陈灿华)

Acoustic and vibration characteristics of vibration reduction double-block ballastless track

WANG Genping, LI Chenghui, CHEN Daixiu, DUAN Haibin

(Ministry of Education Key Laboratory of High-speed Railway Engineering,Southwest Jiaotong University, Chengdu 610031, China)

In order to research frequency-domain properties of vibration attenuation and acoustic radiation vibration of reduction double-block ballastless track, the vibration mechanical model and acoustic boundary element model were established with the method of FEM/BEM. The results show the rail pad has a preponderance of vibration reduction at 200−2 500 Hz, and the damping layer is at 50−3 750 Hz. The ratio of rail acoustic contribution increases with the increase of the frequency, but acoustic radiation of other structures can not be ignored at low frequency. The radiation efficiency of track system structure is complex, which increases at first, then goes stable, and the rail radiation efficiency changes more slowly than others. The acoustic contribution of rail waist is greater than that of rail head and rail base below 125 Hz, and then the acoustic contribution of rail base is greater than that of the other two parts with the increase of the frequency. The noise and vibration prediction are in agreement with those obtained by other models. This work may provide reference for the design of vibration and acoustic reduction track.

vibration reduction double-block ballastless track; finite element method; boundary element method; vibration attenuation; acoustic radiation

10.11817/j.issn.1672−7207.2017.08.037

U211.3；U491.9+1

A

1672−7207(2017)08−2251−06

2016−09−22；

2016−11−26

铁道部科技计划项目(2011S14032)；国家自然科学基金资助项目(51278431)(Project(2011S14032) supported by the Science and Technology Plan of the Ministry of Railways; Project(51278431) supported by the National Natural Science Foundation of China)

李成辉，博士，教授，从事道路与铁道工程研究；E-mail：lichenghui55@163.com