考虑能耗约束的并行机组批调度

李国臣，乔非，王俊凯，马玉敏，卢凯璐

考虑能耗约束的并行机组批调度

李国臣，乔非，王俊凯，马玉敏，卢凯璐

(同济大学电子与信息工程学院，上海，201804)

研究并行批处理机的组批调度问题，考虑炉容相同、功率不同的非等同并行机的总能耗约束，考虑工件尺寸和到达时间不同，以最小化最大完工时间为目标建立混合整数规划模型。并行机组批调度问题属于NP-hard问题，采用先组批后调度的两阶段方式求解。组批阶段采用基于FFLPT和BFLPT的启发式规则，调度阶段设计带邻域搜索的粒子群−遗传混合算法对模型进行求解。以轧辊生产企业并行热处理设备为研究案例进行模型和算法验证，分析不同能耗约束下最大完工时间优化值，并比较算法的优化性能。实验结果表明：本文算法提高标准遗传算法的收敛速度，且优于2种启发式算法；能耗与最大完工时间之间存在冲突关系，通过本文的模型和算法得到能耗与最大完工时间的近似Pareto前沿面，可为企业的实际生产提供指导。

并行机；组批调度；能耗约束；最大完工时间；粒子群-遗传算法；邻域搜索

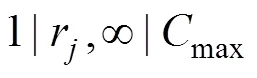
1 并行机组批调度模型

1.1 问题描述

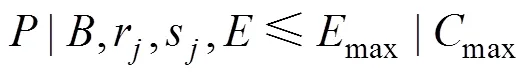
1.2 混合整数规划线性模型

针对工件不同到达时间以及不同尺寸并且考虑能源约束的并行机组批调度问题，优化最大完工时间，建立混合整数线性规划模型(MILP)。模型的目标函数为

Min:max

式中：max为最大完工时间。

约束条件：

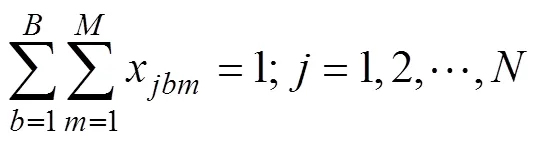
式中：为批处理机数量；为工件数量。约束(1)表示每一个工件都会被分配到某一批次及某一批设备上。

约束(2)表示每个批都会且只能分配到1台机器进行加工。

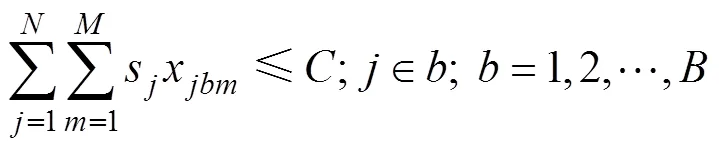
式中：为批处理机的最大容量；s为工件的尺寸，=1，2，…，。约束(3)表示批内工件尺寸总和不能大于批处理机的容量限制。

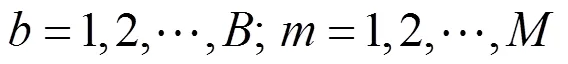
式中：t为工件的加工时间，=1，2，…，；T,P为批次的加工时间，=1，2，…，。约束(4)表示批的加工时间为批内加工时间最长工件的加工时间。

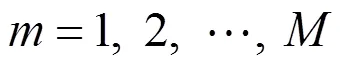
式中：T,S为批次的开始加工时间，=1，2，…，。约束(5)表示最大完工时间大于等于任何一个批的开始加工时间与批加工时间之和，即为最后加工批的完工时间。

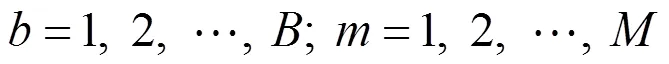
式中：T,R为批次的到达时间，=1，2，…，；t为工件的到达时间，=1，2，…，。约束(6)表示批的到达时间大于等于批内任何工件到达时间。即批的到达时间为批内最晚到达工件的到达时间。

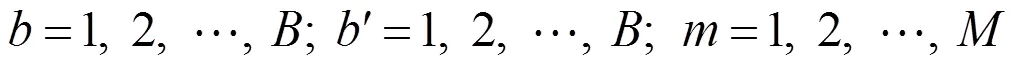
式中：T,C为批次的完工时间，=1，2，…，。约束(7)表示批的开始加工时间为该批的到达时间与该机器内上一个批的完工时间之间的较大值。

式中：e为批处理机的单位时间能耗；E为批处理机的总能耗。

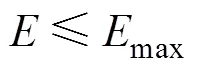
式中：max表示能耗约束值。约束(8)和(9)表示能耗约束，即设备总能耗小于某一上限。

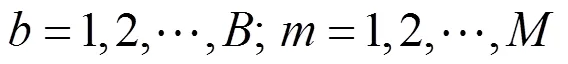
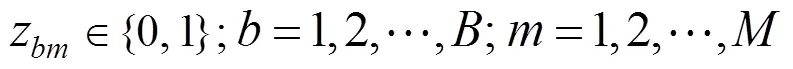
2 模型求解

解决并行机组批调度问题主要有2种方式：第1种是先将加工工件分配到并行处理机，然后进行分批；第2种是先进行组批，然后对组好的批次进行调度。BALASUBRAMANIAN等[7]证明第2种方法能得到更优的解并耗时更少。为了满足生产需要，在短时间内找到满意解。本文采取第2种方式进行求解，第1阶段采用PINEDO[25]提出的最长加工时间最先入批FFLPT和最长加工时间最优入批BFLPT 2种启发式规则。第2阶段采用粒子群算法与遗传算法相结合的方法求解，并结合局部搜索技术提高收敛速度。

2.1 组批阶段算法

PINEDO[25]提出的最长加工时间优先(LPT)规则是求解以Makespan为目标的并行机调度问题较好的算法。对于工件具有不同尺寸的组批问题，当不考虑工件到达时间时，组批调度可以看作是一个装箱问题[5]，对于该问题FFLPT[24]规则和BFLPT[26]规则是2种比较有效的启发式规则。本文采用这2种启发式规则进行组批。

1) FFLPT规则如下。

步骤1：全部工件按照工件加工时间非增排序。

步骤2：选择未分配工件序列中的第1个工件，将该工件分配到第1个可以容纳该工件的批中，若没有找到可以容纳该工件的批，则将该工件放入新建 批中。

步骤3：重复步骤2中的操作，直到所有工件都被分配为止。

2) BFLPT规则如下。

步骤1：全部工件按照工件加工时间非增排序。

步骤2：选择未分配工件序列中的第1个工件，在所有可以容纳该工件的批中，找出剩余容量最小的批次，将该工件放入。

步骤3：重复步骤2中的操作，直到所有工件都被分配为止。

以10个工件为例，分别按照上述分批规则进行分批，表1所示为10个工件的具体属性信息，机器容量设为40。具体实例操作结果如表2和表3所示。

表1 工件详细属性信息

根据FFLPT和BFLPT规则，产生的批次见表2和表3。

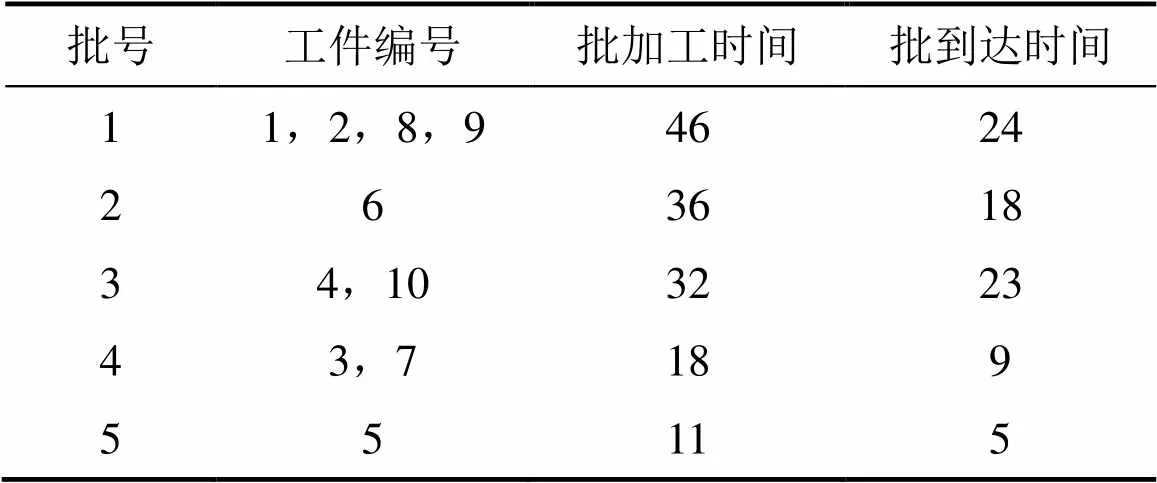
表2 FFLPT规则产生批次

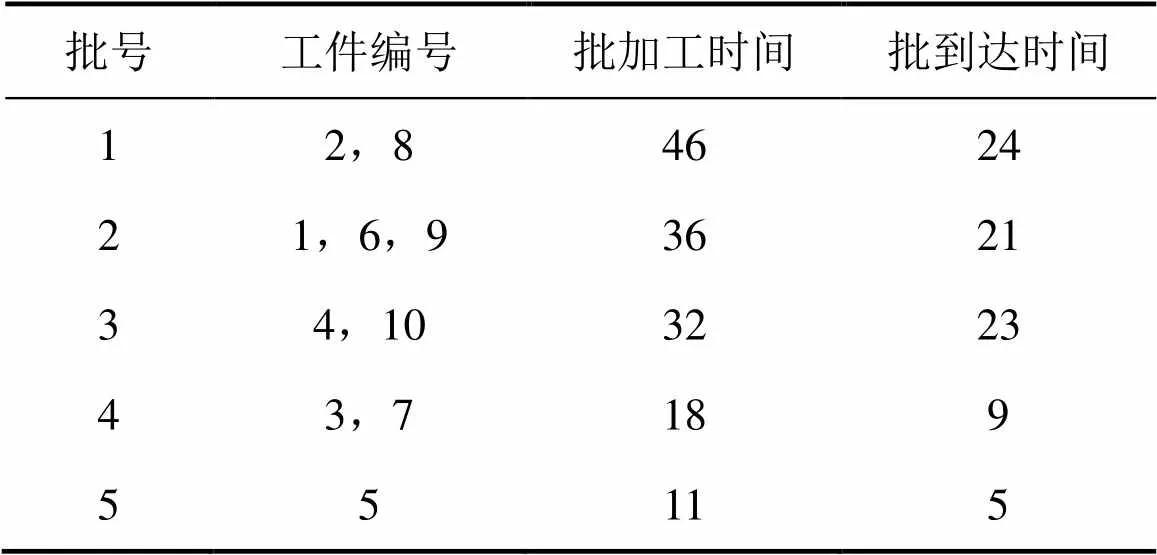
表3 BFLPT规则长生批次

2.2 批次调度阶段算法

经过组批后，所有工件都被安排到对应的加工批次中。由于批次的体积约束在组批阶段中已经满足，故调度阶段算法不再考虑此约束。

粒子群算法，也称粒子群优化算法(PSO)，是近年来发展起来的一种新的进化算法。PSO算法是从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质，相比遗传算法规则更为简单，它没有遗传算法的“交叉”(Crossover)和“变异”(Mutation)操作，它通过追随个体极值和群体极值完成极值来更新粒子的速度和位置从而寻找最优解。

虽然标准粒子群算法操作简单，且能够快速收敛，但是随着迭代次数的不断增加，在种群收敛集中的同时，各粒子也越来越相似，可能在局部最优解周边无法跳出。

遗传和粒子群混合摒弃了传统粒子群算法中的通过跟踪极值来更新粒子速度和位置的方法，而是引入了遗传算法中的交叉和变异操作，通过粒子与个体极值和群体极值的交叉以及粒子自身变异的方式来搜索最优解。同时，为了加快收敛速度，本文引入局部搜索，即用混合遗传算法(Hybrid GA)结合局部搜索来求解并行加热炉的调度问题。批次调度阶段算法流程如图1所示。

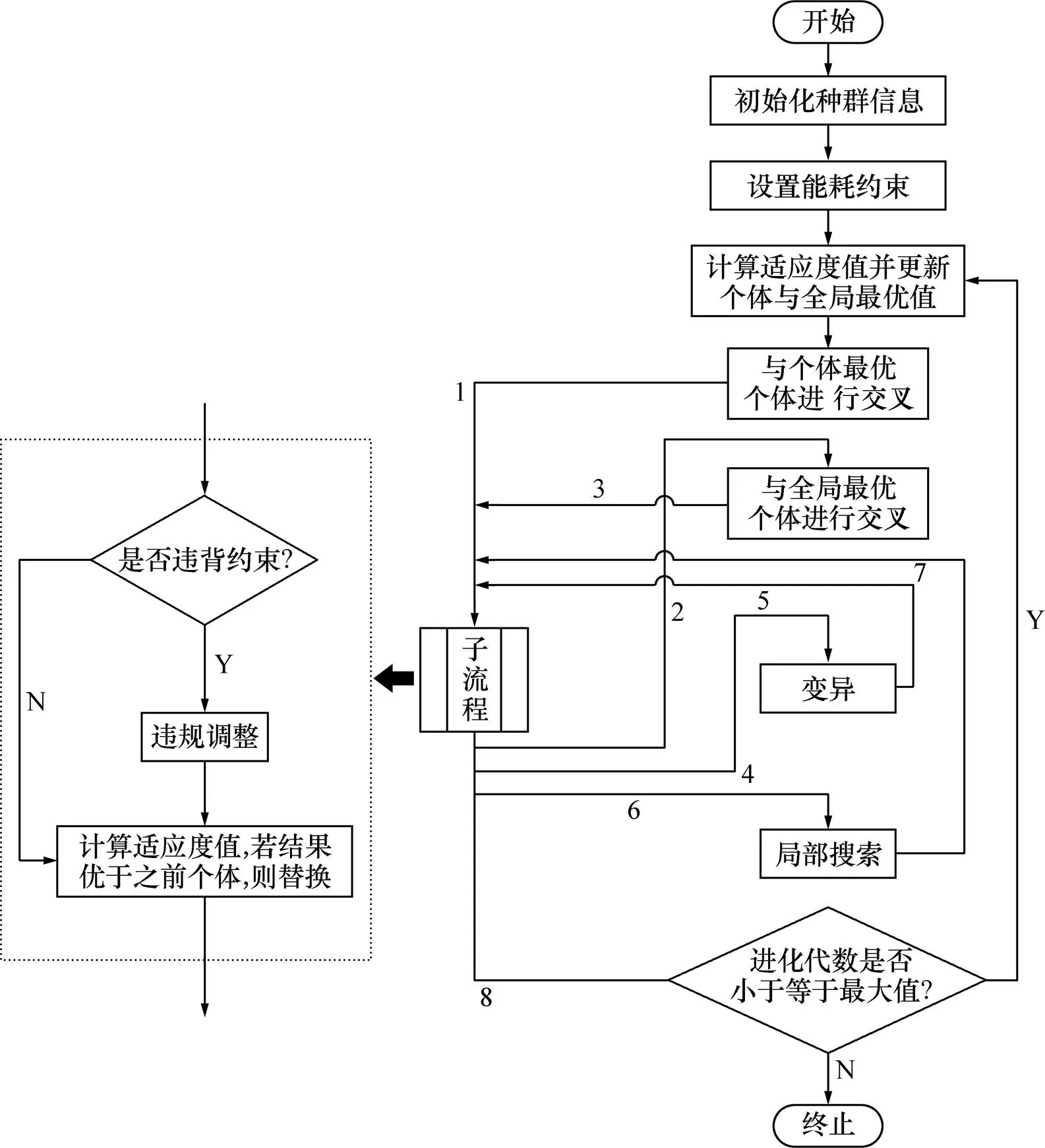
图1 批次调度算法流程图

2.2.1 编码

本阶段以工件批次为操作对象，针对此对象在并行机上进行加工的特点，本文采用实数编码方式，用1个长度为的数组代表个批次，数组中的位置代表相应的工件批次，在工件批次对应的位置赋予批的值，代表该工件被分配到该机器上进行加工。假设有15个工件组批后分配到3个并行机进行加工，一种可能的分配方式可以编码为如下数组：

[1 2 3 1 2 3 1 2 1 3 3 2 1 3 2]

以上编码的解释为：工件批1，4，7，9和13被分配到1号并行机，工件批2，5，8和12被分配到2号并行机，工件批3，6，11和14被分配到3号并行机。

2.2.2 交叉和变异

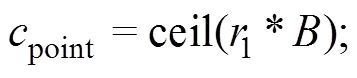
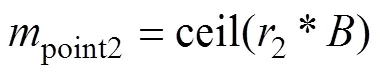
2.2.3 局部搜索策略

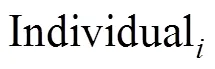
2.2.4 能耗约束

设置能耗约束值，在每次得到新种群的同时计算该种群中每个个体对应的能耗值，若该值超过约束上限，则舍弃该个体，保证种群中所有个体的能耗都在限定范围内。

2.2.5 停止准则

当混合GA满足下面2个条件中的一个时则迭代停止：1) 设定最大进化代数，达到给定的最大代数Iter即终止算法；2) 算法连续进行若干次(Gap次)迭代，在此迭代过程中如果全局最优解(最优个体的适应度值)没有改变，则算法终止。其中Iter和Gap都是由经验给出。

3 案例研究

3.1 参数设置

本文对不同规模(加工工件数量不同)实例分别进行了仿真实验。实验中本文采用CHOU等[20]提出的测试算例。其中，小规模的工件数量=20，中规模和大规模的工件数量分别为=50和100，数据模拟实际生产数据随机产生。以20个轧辊为例，其各种参数值如表4所示。并行批处理机的容积设定为40 m3，机器数量设为3台，3台机器单位能耗分别设为1，2，3(100 kW)。max是根据启发式算法得到的可行解的能耗值设定。最大迭代次数Iter=200，初始种群数目NIND=200。本实验在Matlab 2013a上实现，运行于Windows 7操作系统的PC机(Intel Core i5/ CPU2.4GHZ/RAM 4.0G)上。实验结果如图2~4所示。

以往的不礼貌言语分析主要在语篇层面展开，分析的材料大多是单一的文本资料，较少涉及多媒体资源。多模态话语分析的运用，能够最大程度地还原真实情境下话语互动的内容与意义。这个部分将以Culpeper(2005)的不礼貌策略以及Culpeper et al.(2003)的不礼貌回应策略为理论基础，以视频的图片截图为辅助，来阐释副语言中的视觉以及言语元素在话语意义生成中的相互作用。

3.2 实验结果

图2~4所示分别为不同轧辊规模下并行高温炉的调度结果以及与其他算法结果的对比。为了更清楚的表现本章结果与2种启发式算法和标准GA的对比，不同轧辊规模的能耗与max对应关系都分别绘制了1张局部放大图，可以更清楚地看出本文算法的优越性。

需要说明的是，这里用来对照的2种启发式算法是经过FFLPT和BFLPT组批之后，在批次分配时又采用最早到达时间优先加工的(ERT)规则生成的，分别称之为FFLPTERT和BFLPTERT[5]。选择ERT启发式算法的原因在于，在组批时没有考虑工件的到达时间，而只考虑工件加工时间和尺寸，这可能会造成到达时间差别很大的工件组成一批，影响生产效率。而在将批次分配给并行机加工时需要着重考虑工件的到达时间，比较常用的就是ERT规则。因而，将二者进行组合，有利于降低整个加工流程的完工时间。

表4 轧辊属性值(20个)

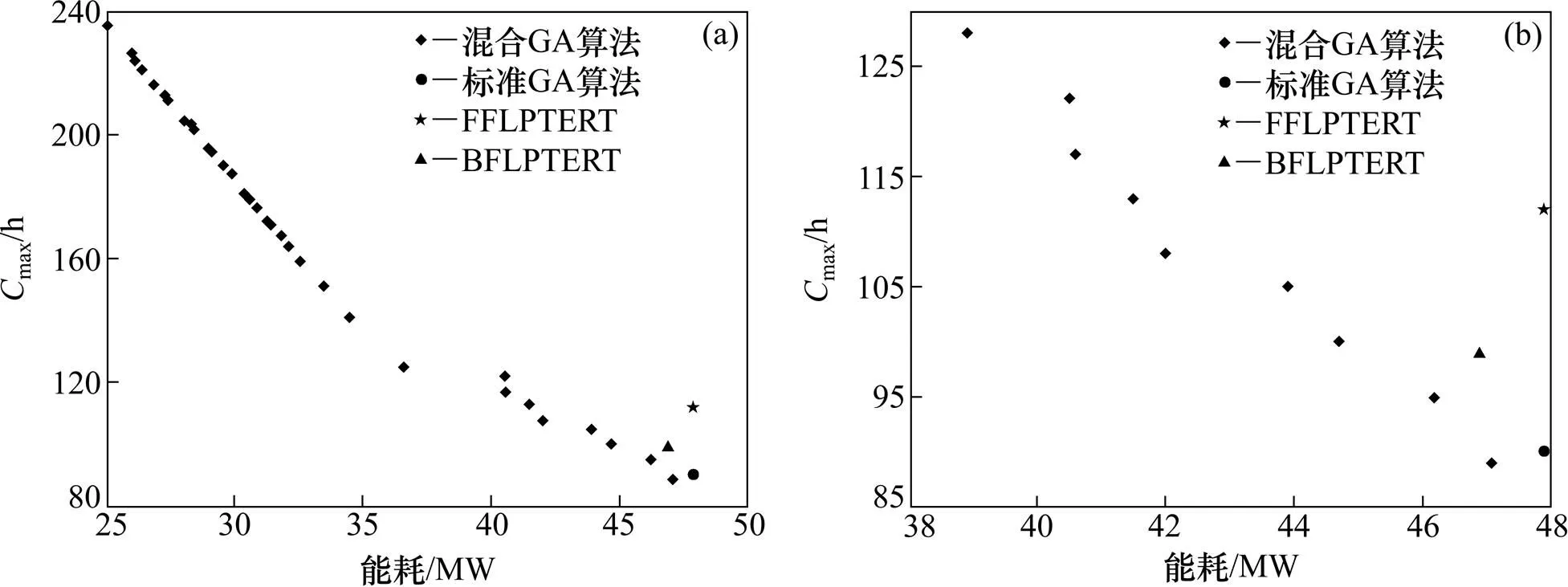
(a) 能耗Cmax对应关系；(b) 能耗与Cmax对应关系局部放大图

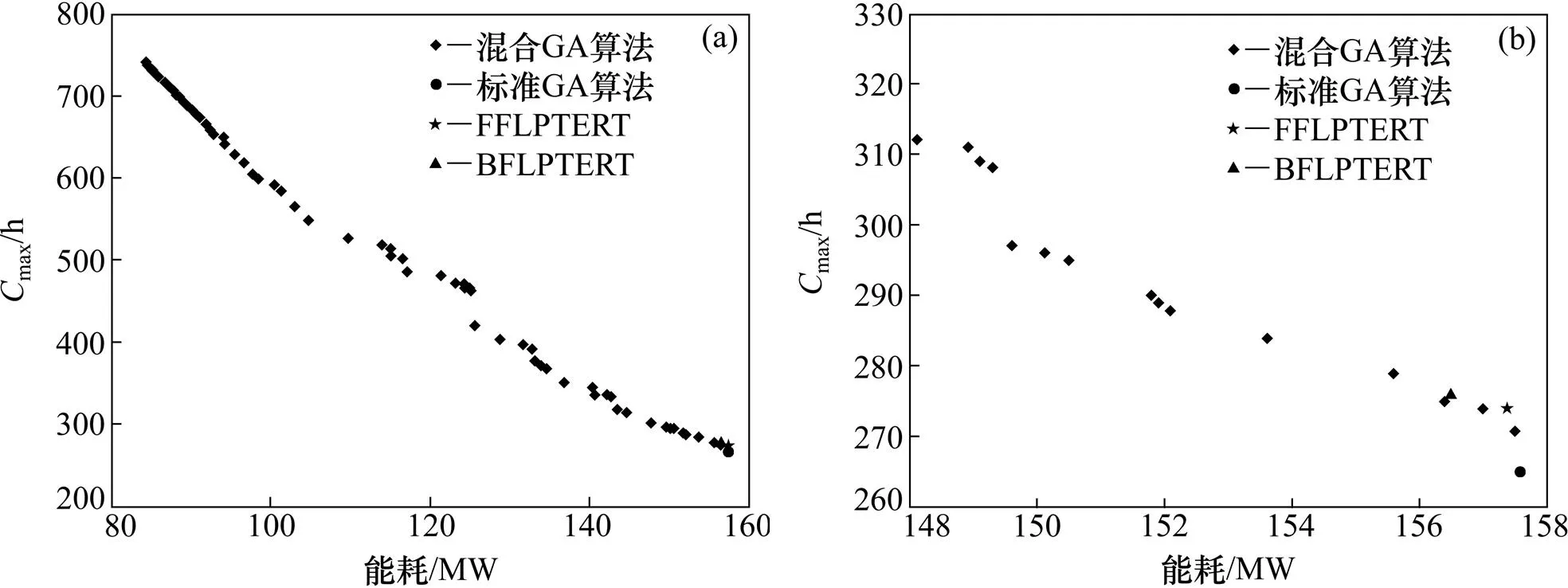
(a) 能耗Cmax对应关系；(b) 能耗与Cmax对应关系局部放大图

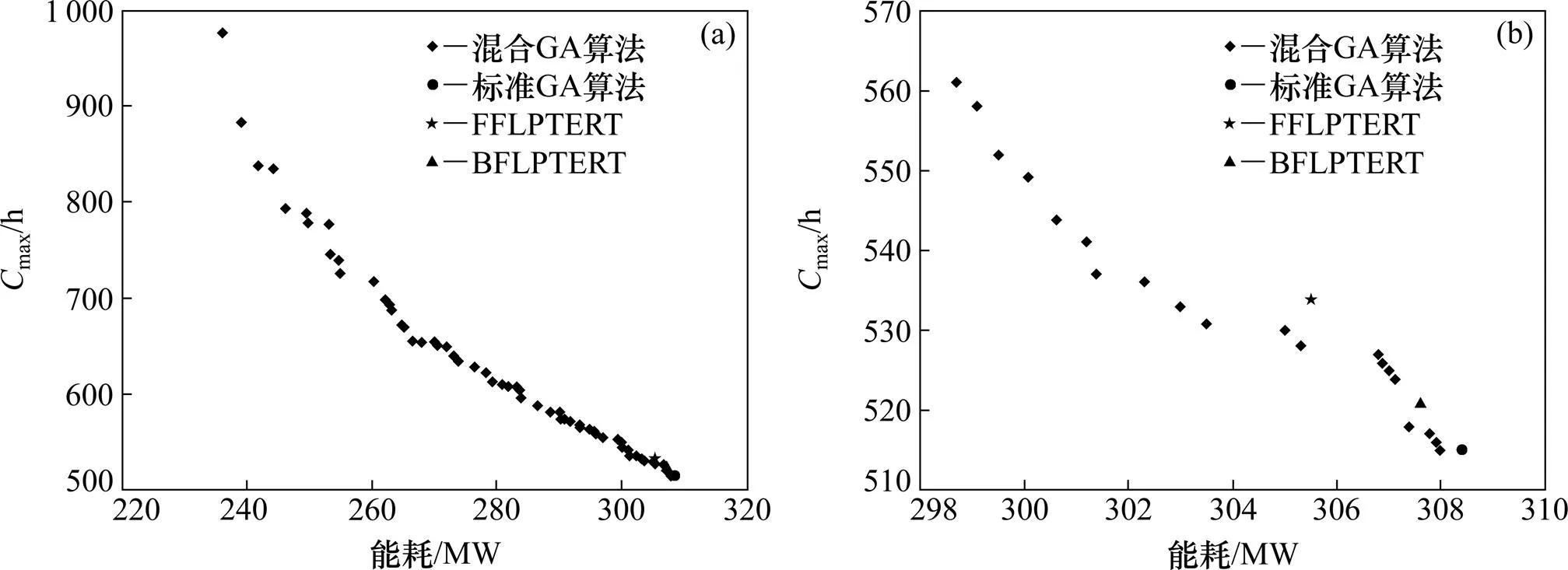
(a) 能耗Cmax对应关系；(b) 能耗与Cmax对应关系局部放大图

FFLPTERT规则如下。

步骤1：将工件按照FFLPT规则组批。

步骤2：全部批次按照批次到达时间非减序排列得到工件序列，其中批次的到达时间以批内最晚到达工件的到达时间为准。

步骤3：将中的工件依次放入第1个空闲的批处理机；若同时有多个机器空闲，则选择功耗最低的机器加工。

步骤4：重复步骤3中的操作，直到所有批都被分配。

从图2~4可见：星形点形成了混合GA在不同能耗约束下的max走势图，近似于Pareto前沿面，可以发现2类指标之间存在冲突关系；而其他几种算法由于不考虑能耗因素，故仅能得到各自唯一的max优化值，然后计算得到相应的能耗。混合GA得到的近似Pareto前沿面上的解位于其他算法得到的解的左下方，说明该前沿面上的解对其他算法的解都是占优的，即在相同的能耗约束值下，提出的算法取得了更小的max。同时，其他算法求得的解对应的能耗值往往较高，位于横坐标右端，说明这些算法无法应对总能耗有限制的情况；而本章提出的协同模型可以在不同的能耗约束下到相应的max优化解，满足了生产需求。以100个轧辊为例，图4显示了不同能耗约束下优化得到的最优max散点图，实际生产中可以根据不同的总能耗约束要求选择相应的生产方案。

同样以100个轧辊的案例为例，由表7可以看出：本文算法可以找出max和能耗均优于2种启发式算法的解。例如表7中第7列的解max与能耗相对BFLPTERT算法分别降低0.579%和0.065%；而第3列中的解相对于FFLPTERT算法max和能耗分别降低0.565%和0.659%；第4列的解max与能耗相对FFLPTERT算法分别降低0.755%和0.164%，证明了本算法的有效性。

不过，有些解的表现则有所不同，例如第3列的解相对于BFLPTERT算法max虽提高1.883%，但是能耗却降低1.351%，相对于标准GAmax虽提高3.013%，但是能耗却降低1.614%；同样第8列的解相对于FFLPTERT算法能耗虽提高0.747%，但max降低3.288%，相对于标准GA，max虽提高0.387%，但能耗降低0.195%。这说明max和总能耗存在冲突关系，即追求max的降低可能引起能耗的增加。反之亦然。

表5 混合GA相对于其他算法的降低比例(20个工件)

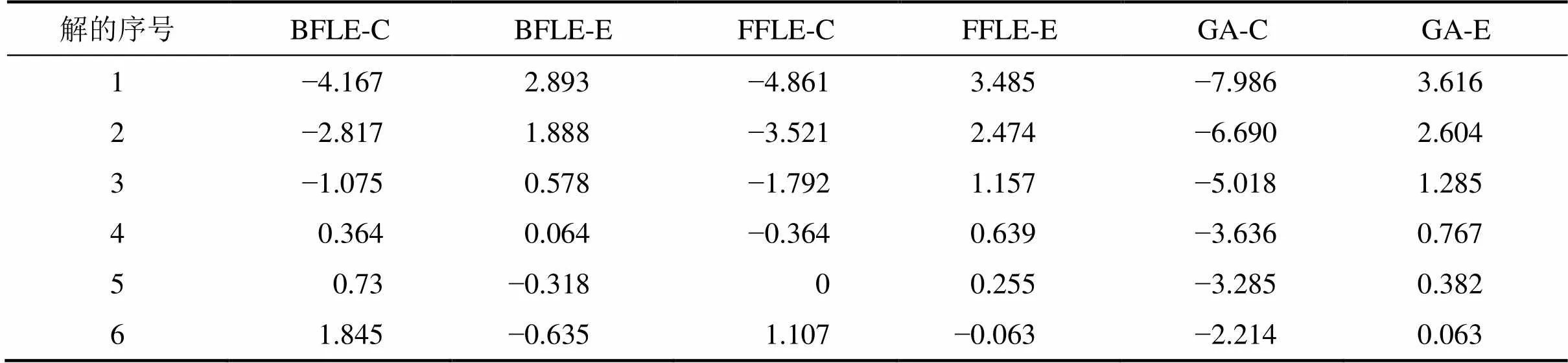
表6 混合GA相对于其他算法的降低比例(50个工件)

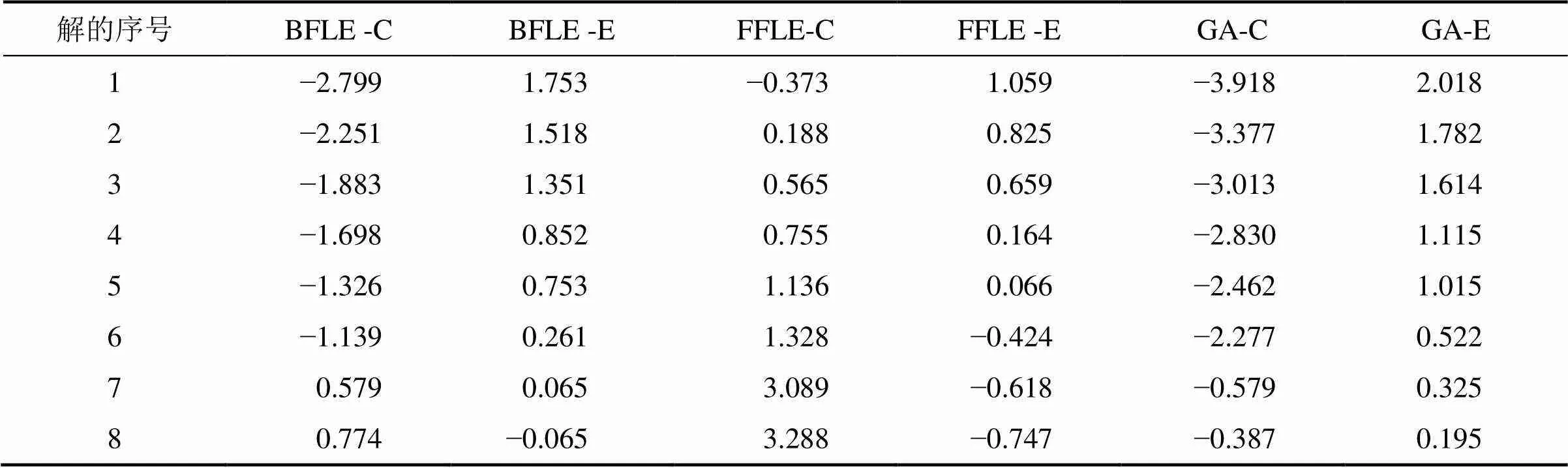
表7 混合GA相对于其他算法的降低比例(100个工件)

综合比较表5~7可知：无论对比启发式算法还是标准GA，都可看出随着轧辊数量的增加混合GA的优化比例逐渐减小。这说明随着轧辊数量的增加，问题的求解难度剧增，混合GA的寻优能力略有减弱。故未来可以继续研究大规模问题下更为有效的求解算法。

4 结论

1) 所提算法能够高效地寻找到各个能耗约束下的最优max，与2种经典启发式算法及标准GA对比优化效果明显。

2) 混合GA算法在问题规模较小时优势明显，随着轧辊数量的增加，混合GA算法的优势略有下降。

3) 为了应对企业供能限制，在约束中加入总能耗约束，使得企业在实际生产时可以根据能耗供应要求选择最大完工时间最小的生产方案。

[1] IEA. Tracking industrial, energy efficiency and CO2Emissions. [2007−09].http://www.iea.org/textbase/nppdf/free/2007/tracking_ emissions.pdf.

[2] JOVANE F, YOSHIKAWA H, ALTING L, et al. The incoming global technological and industrial revolution towards competitive sustainable manufacturing[J]. Annals of the CIRP, 2008, 57(2): 641−659.

[3] 朱祝林. 以能源节约为目标的轧辊热处理过程中若干调度优化方法研究[D]. 沈阳: 东北大学信息科学与工程学院, 2011: 1−60. ZHU Zhulin. Scheduling optimization methods for thermal treatment process in mill roller production aiming at energy conservation[D]. Shenyang: Northeastern University. College of Information Science and Engineering, 2011: 1−60.

[4] LIU C H. Approximate trade-off between minimisation of total weighted tardiness and minimisation of carbon dioxide (CO2) emissions in bi-criteria batch scheduling problem[J]. International Journal of Computer Integrated Manufacturing, 2014, 27(8): 759−771.

[5] 李小林. 平行机环境下批处理调度问题研究[D]. 合肥: 中国科学技术大学管理科学与工程, 2012: 1−25. LI Xiaolin. Research on scheduling batch processing machines in parallel[D]. Hefei: University of Science and Technology of China, Management Science and Engineering, 2012: 1−25.

[6] MALVE S, UZSOY R. A genetic algorithm for minimizing maximum lateness on parallel identical batch processing machines with dynamic job arrivals and incompatible job gamilies[J]. Computers & Operations Research, 2007, 34(10): 3016−3028.

[7] BALASUBRAMANIAN H, MONCH L, FOWLER J W, et al. Genetic algorithm based scheduling of parallel batch machines with incompatible job families to minimize total weighted tardiness[J]. International Journal of Production Research 2004, 42(8): 1621−1638.

[8] YILMAZ E D, OZMUTLU H C, OZMUTLU S. Genetic algorithm with local search for the unrelated parallel machine scheduling problem with sequence-dependent set-up times[J]. International Journal of Production Research, 2014, 52(19): 5841−5856.

[9] VALLADA E, RUIZ R. A genetic algorithm for the unrelated parallel machine scheduling problem with sequence dependent setup times[J]. European Journal of Operational Research, 2011, 211(3): 612−622.

[10] TANAKA S, ARAKI M. A branch-and-bound algorithm with Lagrangian relaxation to minimize total tardiness on identical parallel machines[J]. International Journal of Production Economics, 2008, 113(1): 446−458.

[11] CHAUDHRY I A, DRAKE P R. Minimizing total tardiness for the machine scheduling and worker assignment problems in identical parallel machines using genetic algorithms[J]. The International Journal of Advanced Manufacturing Technology, 2009, 42(5): 581−594.

[12] 刘民, 吴澄, 蒋新松. 用遗传算法解决并行多机调度问题[J]. 系统工程理论与实践, 1998, 18(1): 14−17. LIU Min, WU Cheng, JIANG Xinsong. Genetic algorithm method for identical parallel machine scheduling problem[J]. System Engineering-Theory & Practice, 1998, 18(1): 14−17.

[13] WANG L Y, HUANG X, JI P, et al. Unrelated parallel-machine scheduling with deteriorating maintenance activities to minimize the total completion time[J]. Optimization Letters, 2014, 8(1): 129−134.

[14] KASHAN A H, KARIMI B. A discrete particle swarm optimization algorithm for scheduling parallel machines[J]. Computers & Industrial Engineering, 2009, 56(1): 216−223.

[15] YEH W C, LAI P J, LEE W C, et al. Parallel-machine scheduling to minimize makespan with fuzzy processing times and learning effects[J]. Information Sciences, 2014, 269: 142−158.

[16] UZSOY R, YANG Y. Minimizing total weighted completion time on a single processing machine[J]. Production and operations Management, 1997, 6(1): 57−73.

[17] AZIZOGLU M, WEBSTER S. Scheduling a batch processing machine with non-identical job sizes[J]. International Journal of Production Research, 2000, 38(10): 2173−2184.

[18] 程八一, 陈华平, 王栓狮. 基于微粒群算法的单机不同尺寸工件批调度问题求解[J]. 中国管理科学, 2008, 16(3): 84−88. CHENG Bayi, CHEN Huaping, WANG Shuanshi. Scheduling a single batch-processing machine with non-identical job sizes based on practice swarm optimization[J]. Chinese Journal of Management Science, 2008, 16(3): 84−88.

[19] LEE C Y, UZSOY R. Minimizing makespan on a single batch processing machine with dynamic job arrivals[J]. International Journal of Production Research, 1999, 37(l): 219−236.

[20] CHOU F D, CHANG P C, WANG H M A. Hybrid genetic algorithm to minimize makespan for the single batch machine dynamic scheduling problem[J]. International Journal of Advanced Manufacturing Technology, 2006, 31(3): 350−359.

[21] LI S G, LI G J, WANG X L, et al. Minimizing makespan on a single batching machine with release times and non-identical job sizes[J]. Operations Research Letters, 2005, 33(2): 157−164.

[22] 姜冠成. 带到达时间分批排序问题的数学模型[J]. 苏州大学学报, 2005, 21(2): 22−27. JIANG Guancheng. Formulating the batch scheduling with release time as a mathematical programming model[J]. Journal of Suzhou University, 2005, 21(2): 22−27.

[23] GRAHAM R, LAWLER E, LENSTRA J, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Annals of Discrete Mathematics, 1979, 5(2): 287−326.

[24] UZSOY R. Scheduling a single batch processing machine with non-identical job sizes[J]. International Journal of Production Research, 1994, 32(7): 1615−1635.

[25] PINEDO M L. Scheduling theory, algorithms, and systems[M]. 3th ed, New York, USA: Springer, 2008: 1−52.

[26] DUPONT L, DHAENENS-FLIPO C. Minimizing the makespan on a batch machine with non-identical job sizes: an exact procedure[J]. Computers & Operations Research, 2002, 29(7): 807−819.

(编辑 陈爱华)

Parallel machine batching scheduling considering energy constraints

LI Guochen, QIAO Fei, WANG Junkai, MA Yumin, LU Kailu

(College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

Non-identical parallel machines with same capacity but different power were considered for batching scheduling problems. A mixed integer programming model minimizing makespan was established, with different job sizes and arrival times. As the parallel machine batching scheduling problem was NP-hard, a two-phase method, that was, first batching and then scheduling, was adopted to solve the model. At the phase of batching, two heuristic rules, FFLPT and BFLPT, were employed; and a PSO-GA hybrid algorithm with neighborhood search was designed at the phase of scheduling. The proposed model and algorithm were validated under a case study of parallel heat treatment equipment in roller manufacturing. Optimized makespans under different energy consumption constraints were analyzed, and the performance of different algorithms were compared. The results show that the proposed algorithm improves the convergent speed of standard genetic algorithm, and outperforms the other two heuristic algorithms. Meanwhile, there exists trade-offs between energy consumption and makespan. And the approximate Pareto frontier of these two indicators obtained by the proposed model and algorithm may provide guidance for real production in enterprises.

parallel machines; batch scheduling; energy consumption constraints; makespan; PSO-GA; neighborhood search

10.11817/j.issn.1672−7207.2017.08.013

O221.4

A

1672−7207(2017)08−2063−10

2016−09−25；

2016−12−20

国家自然科学基金资助项目(71690234，61273046)(Projects (71690234, 61273046) supported by the National Natural Science Foundation of China)

乔非，博士，教授，从事生产调度优化、高能效制造研究；E-mail：fqiao@tongji.edu.cn