涉及q-差分微分多项式的亚纯函数的唯一性*
2017-11-01李效敏刘雪峰徐会彩孙银龙
李效敏, 刘雪峰, 徐会彩, 孙银龙
( 1.中国海洋大学数学科学学院, 山东 青岛 266100; 2.中国人民大学信息学院, 北京 100872)
涉及q-差分微分多项式的亚纯函数的唯一性*
李效敏1, 刘雪峰1, 徐会彩2, 孙银龙1
( 1.中国海洋大学数学科学学院, 山东 青岛 266100; 2.中国人民大学信息学院, 北京 100872)
本文研究亚纯函数及其q-差分算子或差分算子的1类非线性多项式的导函数分担1个非零公共值的亚纯函数的唯一性问题,这些问题涉及2009年方明亮提出的1个涉及微分多项式的亚纯函数的唯一性问题。本文结果推广了方明亮等人的有关结果。
q-差分多项式;微分多项式;零级亚纯函数;唯一性定理



1976年,杨重骏提出了下述问题:
问题2[4]假设f与g是2个非常数的整函数,n是1个正整数。如果f与gCM分担0,f(n)与g(n)CM分担1,并且2δ(0,f)>1,那么f与g的关系如何?
1990年,仪洪勋解决了问题2,证明了下述定理:
定理3[5]假设f与g是2个非常数的整函数,n是1个正整数。如果f与gCM分担0,f(n)与g(n)CM分担1,并且2δ(0,f)>1,那么f=g或者f(n)g(n)=1。
1997年,I. Lahiri提出了下述问题:
问题4[6]如果2个非常数的亚纯函数的非线性微分多项式CM分担1,那么这2个亚纯函数的关系如何?
1997年,杨重骏和华歆厚研究了问题4,证明了下述定理:
定理5[7]假设f与g是2个非常数的亚纯函数,n是1个正整数且满足n≥11。如果fnf′与gng′CM分担1,那么f与g满足下述2种情形之一:(i)f=tg,其中t是一个常数,且满足tn=1;(ii)f=c1ecz,g=c2e-cz,其中c,c1和c2是非零常数,且满足(c1c2)n+1c2=-1。
2002年,方明亮证明了下述结果,在整函数条件下研究了问题4,证明了下述定理:
定理6[8]假设f与g是2个非常数的整函数,n与k是2个正整数且满足n≥2k+8。如果(fn(f-1))(k)与(gn(g-1))(k)CM分担1,那么f=g。
2009年,方明亮在华东师范大学复分析会议上提出了下述问题:
问题7 假设f与g是2个非常数的亚纯函数,n,k是2个正整数且满足n>3k+11。如果(fn(f-1))(k)与(gn(g-1))(k)CM分担1,那么是否有f=g?
截止到目前,问题7还没有得到彻底解决。近几年来Halburd-Korhonen[9]以及冯绍继与蒋翼迈[10]分别建立了差分Nevanlinna理论,Laine-Yang[11]得到了涉及差分多项式的Clunie定理。应用这些理论,一些芬兰学者和中国学者开始了差分唯一性理论的研究[12-14]。本文将利用q-差分Nevanlinna理论,结合微分多项式具有一个非零公共值的亚纯函数唯一性问题的研究方法,研究1类q-差分微分多项式具有一个非零公共值的亚纯函数的唯一性问题,具体说来,本文将研究下述几个问题:

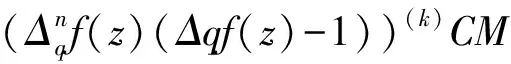
问题10 在问题8中,如果(fn(z)(f(z)-1))(k)与(fn(qz)(f(qz)-1))(k)IM分担1,其它条件不变,那么n,k在满足什么条件下,有结论f(z)=f(z+η)。

本文将研究问题8-问题11,并首先证明下述两个定理:

定理13 假设f(z)是1个非常数的零级亚纯函数,Δqf(z)=f(qz)-f(z)是f(z)的q-差分算子,其中q是一个非零复数。如果(fn(z)(f(z)-1))(k)与((Δqf(z))n(Δqf(z)-1))(k)CM分担1,其中n和k是两个正整数且满足n>3k+11,并且Θ(∞,f)>2/n,那么f(z)=Δqf(z)。
用证明定理12和定理13的类似方法和本文引理11可得下述两个定理:


1 几个引理
引理1[1,Theorem3.2]假设f是1个非常数的亚纯函数,k是1个正整数,c≠0是1个有限值,那么



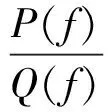
T(r,F)=max{p,q}T(r,f)+O(1)。
引理3[16,引理2.3的证明]假设F是1个非常数的亚纯函数,k与p是2个非常数的正整数,那么

引理4 假设f与g是2个非常数的亚纯函数,n和k是2个正整数且满足n>3k+11。如果(fn(f-1))(k)与(gn(g-1))(k)CM分担1,那么(fn(f-1))(k)(gn(g-1))(k)=1或者(fn(f-1))(k)=(gn(g-1))(k)。
证明 置
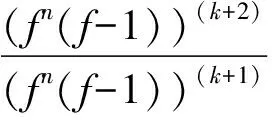
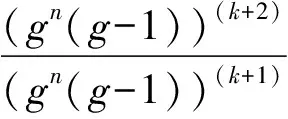
(1)
情形1 假设H不恒等于零。
设z0是(fn(z)(f(z)-1))(k)与(gn(z)(g(z)-1))(k)的一个公共单零点。将(fn(z)(f(z)-1))(k)与(gn(z)(g(z)-1))(k)在z0点的Taylor展示代入(1)可知,z0是H的零点。于是再由(1)及引理4的条件可得
T(r,H)+O(1)≤
N(r,H)+m(r,H)+O(1)≤
S(r,f)+S(r,g),
(2)
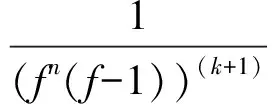
(n+1)T(r,f)+O(1)=T(r,fn(f-1))≤


即
(n+1)T(r,f)≤

(3)
同理
(n+1)T(r,g)≤

(4)
再由(2)和引理4的已知条件可得





即

(5)
将(5)代入(3)和(4)相加所得的不等式的右边,并整理得
(n+1)T(r,g)≤


(6)
同理
(n+1)T(r,f)≤


(7)
由(6)和(7)可得



由此得n≤3k+11,这与已知条件n>3k+11矛盾。
情形2 假设H=0。由(1)可得
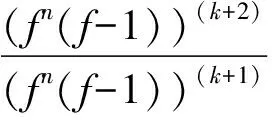
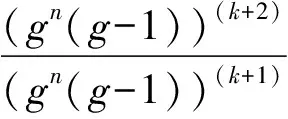
(8)
由(8)连续积分两次可得

(9)
其中a和b是两个常数,并且a≠0。分三种子情形讨论如下:
子情形2.1 假设a=b。如果b=-1,由(9)
可得(fn(f-1))(k)(gn(g-1))(k)=1,
于是引理4的结论成立。
如果b≠-1,那么(9)可变为

(10)
由(10)可得
(11)
由(11)和引理1,引理2和引理3可得
(n+1)T(r,g)=T(r,gn(g-1))+O(1)≤

(12)
同理可得


(13)
由(12)和(13)可得
n(T(r,f)+T(r,g)) ≤

(2k+4)(T(r,f)+T(r,g))+S(r,f)+S(r,g),
由此可得n≤2k+4,这与已知条件n>3k+11矛盾。
子情形2.2 假设a≠b并且b≠0。如果b=-1,那么(9)变为

(14)
由于(fn(f-1))(k)与(gn(g-1))(k)CM分担1,由(14)可得
(n+1)T(r,g)=T(r,gn(g-1))+O(1)≤

(k+3)T(r,g)+T(r,f)+S(r,g),
于是
(n-k-2)T(r,g)≤T(r,f)+S(r,g)。
(15)
另一方面,再将(14)改写成

(16)
由(16)和引理3可得
(n+1)T(r,f)=T(r,fn(f-1))+O(1)≤

(k+3)T(r,f)+(k+3)T(r,g)+S(r,f),
于是
(n-k-2)T(r,f)≤(k+3)T(r,g)+S(r,f)。
(17)
由(15),(17)和条件n>3k+11可得矛盾。
如果b≠-1,那么(9)变为
(fn(f-1))(k)-(1+1/b)=

(18)
由(18),类似于(14)条件下的推导过程可得矛盾。
子情形2. 3 假设a≠b并且b=0。由(9)可得
a(fn(f-1))(k)=(gn(g-1))(k)。
(19)

如果1不是(fn(f-1))(k)与(gn(g-1))(k)的Picard例外值,则存在(fn(f-1))(k)与(gn(g-1))(k)的公共1-值点z1,使得(f(z)n(f(z)-1))(k)|z=z1=(g(z)n(g(z)-1))(k)|z=z1=1,该式结合(19)可的a=1,于是引理4的结论成立。以下假设f,g是两个超越亚纯函数。一方面,由(19)可得
afn(f-1)=gn(g-1)+P1,
(20)
其中P1是一个次数不超过k的多项式。假设P1不恒等于零,由(20),引理1和引理2可得
T(r,f)=T(r,g)+O(logr),
(21)
和
(n+1)T(r,f)=T(r,fn(f-1))+O(1)≤
S(r,f)≤

(k+3)T(r,f)+(k+3)T(r,g)+S(r,f)。
(22)
由(21)和(22)可得n≤2k+5,这与n>3k+11矛盾。于是P1=0,(20)变为afn(f-1)=gn(g-1),由此得
a(fn(f-1))(k)=(gn(g-1))(k)。
(23)
另外,由前面得到的(3)可得
(n-k-2)T(r,f)≤
(24)
由(24)可知(fn(f-1))(k)-1有零点。注意到(fn(f-1))(k)与(gn(g-1))(k)CM分担1,由(23)可知a=1,于是引理4成立。引理4证毕。
引理5[17]

在对数密度是1的集合上成立。
引理6[18,Theorem1. 1]假设f是1个非常数的零级亚纯函数,则在下对数密度为1的集合上有T(r,f(qz))=T(r,f(z))(1+o(1))。
引理7[18,Theorem1. 3]假设f是1个非常数的零级亚纯函数,则在下对数密度为1的集合上有N(r,f(qz))=N(r,f(z))(1+o(1))。

如果C1>1,C2>1,那么集合E={r:T(C1r)≥C2T(r)}的对数密度为零。

引理10[20]假设s>0和t是2个互素的整数,c是一个满足cs=1的复数,那么ωs-1与ωt-c有且只有一个公共零点。
引理11[21]假设f与g是2个非常数的亚纯函数,k≥1是一个正整数,并且f(k)与g(k)IM分担1。如果
Δ1=(2k+3)Θ(∞,f)+(2k+4)Θ(∞,g)+Θ(0,f)+Θ(0,g)+2δk+1(0,f)+3δk+1(0,g)>4k+13
和
Δ2=(2k+3)Θ(∞,g)+(2k+4)Θ(∞,f)+Θ(0,g)+Θ(0,f)+2δk+1(0,g)+3δk+1(0,f)>4k+13
成立,那么f(k)g(k)=1或者f=g。
2 定理的证明
定理13的证明 设f(qz)-f(z)=g(z)。由引理4,分两种情形讨论如下:
情形1 假设
((f(z)n(f(z)-1))(k)((f(qz)-f(z))n(f(qz)-f(z)-1))(k)=1。
(25)
首先,(fn(f-1))(k)不恒等于常数。事实上,若(fn(f-1))(k)恒等于某个常数,那么
fn(f-1)=Pk,
(26)
其中Pk是某个次数≤k的多项式。注意到f是一个非常数的亚纯函数,并且n>3k+11,无论f是有理函数还是超越亚纯函数,我们都可以由(26)和引理2得出矛盾。设

(27)
则由(27)可知f(qz)-f(z)=f(z)(h(z)-1),于是(25)可写成
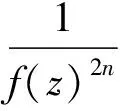

(28)
其中
h1=(h-1)n(f-1)(f(h-1)-1)。
(29)
于是由(28),(29)和引理5可得
m(r,h1(z))+o(T(r,f))≤
2m(r,f(z))+o(T(r,f))。
(30)
另一方面,由(25)和条件n>3k+11可知,f(z)的每个极点一定是f(qz)的极点,而Δqf(z)=f(qz)-f(z)的极点是f(z)的解析点,从而由引理7可知
N(r,Δqf(qz))≤N(r,f(qz))-N(r,f(z))=o(T(r,f))。
(31)
在r的下对数密度为1的集合上成立。
再由(25),(31)和条件n>3k+11可得
N(r,((Δqf(z))n(Δqf(z)-1))(k))≤

o(T(r,f)),
从而
(32)
在下对数密度为1的集合上成立。再由(30),(32)和第一基本定理可得
2m(r,f(z))+o(T(r,f))≤2T(r,f(z))+o(T(r,f))
在r的下对数密度为1的集合上成立。
该式结合条件n>3k+11可得T(r,f)=o(T(r,f))在r的下对数密度为1的集合上成立,从而f为常数函数,这与已知条件矛盾。
情形2 假设
(fn(f-1))(k)=(gn(g-1))(k),
(33)
其中g(z)=f(qz)-f(z)。
(34)
由(33)可得
fn(f-1)-gn(g-1)=Qk。
(35)
其中Qk是一个次数不超过k的多项式。如果Qk不恒为零,由(35),引理2和引理9可得

和(n+1)T(r,f)=T(r,fn(f-1))+O(1)≤


该式与条件n>3k+11可知,不论f是非常数的有理函数还是超越亚纯函数,均可得到矛盾。所以Qk=0,于是(35)变为
fn(f-1)=gn(g-1)。
(36)
假设f不恒等于g。设

(37)
以下分两子种情形讨论:
子情形2.1 假设h是一个常数,那么h≠1,于是1-hn+1和1-hn+1不同时为零。由(36)和(37)可得(1-hn+1)g=1-hn,于是(1-hn+1)(1-hn)≠0,从而

(38)
这与g为非常数的亚纯函数矛盾。
子情形2.2 假设h不恒为常数,那么h-1,1-hn+1和1-hn全不恒为零,于是由(36)和(37)可得(38)。由引理10可知,1-ωn+1和1-ωn有且只有一个公共零点ω=1。由此结合(38)和引理2可得

(39)
于是S(r,f)=S(r,h)。由第二基本定理可得
(n-2)T(r,h)+S(r,h),
(40)
其中,αj(1≤j≤n)是ωn+1=1的n个判别的根并且αj≠1。于是由(39)(40)可得
这与已知条件Θ(∞,f)>2/n矛盾。于是f=g,即f=Δqf。从而完成了定理13的证明。
定理12的证明:
由引理4,分两种情形讨论如下:
情形1 假设
(f(z)n(f(z)-1))(k)(f(qz)n(f(qz)-1))(k)=1。
(41)
首先类似于定理13证明过程中的情形1可得(fn(f-1))(k)和(f(qz)n(f(qz)-1))(k)均不恒为常数。再由(41),引理3,引理5和引理6可得

N(r,(f(z)n(f(z)-1)(k))=



(k+1)T(r,f(qz))+T(r,f(qz)-1)+

(k+2)T(r,f(qz))+S(r,f(z))≤


(k+2)T(r,f(z)+S(r,f(z))。
(42)
由引理8可得

(43)
由(42)和(43)可得

(44)
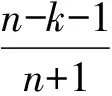
情形2 假设
(f(z)n(f(z)-1))(k)=(f(qz)n(f(qz)-1))(k)。
(45)
由(45),类似于定理13的证明过程中情形2可得f(z)=f(qz),于是完成了定理12的证明。
[1] Hayman W K. Meromorphic Functions[M]. Oxford:The Claredon,1964.
[2] 仪洪勋,杨重骏. 亚纯函数的唯一性理论[M]. 北京:科学出版社,1995.
Hong-Xun Yi, Chung-Chun Yang. Uniqueness Theory of Meromorphic Functions[M]. Beijing: Science Press, 1995.
[3] I Lahiri. Weighted sharing of three values and uniqueness of meromorphic functions[J]. Kodai. Math. J.,2001,24 (3): 421-435.
[4] C C Yang. On two entire functions which together with their derivatives have the same zeros[J]. J Math Anal Appl, 1976, 56: 1-6.
[5] H X Yi. Uniqueness of meromorphic functions and a question of C.C. Yang[J]. Complex Var Theory Appl, 1990, 14: 169-176.
[6] I Lahiri. Uniqueness of meromorphic functions as governed by their differential polynomials[J]. Yokohama Math. J.,1997, 44: 147-156.
[7] C C Yang, X H Hua. Uniqueness and value-sharing of meromorphic functions[J]. Ann Acad Sci Fenn Math, 1997, 22: 95-406.
[8] M L Fang. Uniqueness and value sharing of entire functions[J]. Comput Math Appl, 2002, 44: 823-831.
[9] R Halburd, R Korhonen, K Tohge. Holomorphic curves with shift-invariant hyperplane preimages[J]. Trans Amer Math Soc, 2014, 366 (8): 4267-4298.
[10] Y M Chiang, S J Feng. On the Nevanlinna characteristic of and difference equations in the complex plane[J]. Ramanujan J, 2008, 16: 105-129.
[11] I Laine, C C Yang. Clunie theorems for difference and q-difference polynomials[J]. J London Math Soc, 2007, 76: 556-566.
[12] J Heittokangas, R Korhonen, I Laine, et al. Value sharing results for shifts of meromorphic functions and sufficient conditions for periodicity[J]. J Math Anal Appl, 2009, 355: 352-363.
[13] J Heittokangas, R Korhonen, I Laine, et al. Uniqueness of meromorphic functions sharing values with their shifts[J]. Complex Var Elliptic Equ, 2011, 56: 81-92.
[14] J L Zhang. Value distribution and shared sets of differences of meromorphic functions[J]. J Math Anal Appl, 2010, 367: 401-408.
[15] A Z Mokhon′ko. On the Nevanlinna characteristics of some meromorphic functions[C]. //Theory of Functions, Functional Analysis and Their Applications, Izd-vo Khar′kovsk. Un-ta, 1971, 14: 83-87.
[16] I Lahiri, A Sarkar. Uniqueness of a meromorphic function and its derivative[J].J Inequal Pure Appl Math, 2004, 5 (1): 20.
[17] D Barnett, R G Halburd, R J Korhonen, et al. Applications of Nevanlinna theory to q-difference equations[J]. Proc Roy Soc Edinburgh Sect A, 2007, 137: 457-474.
[18] J Zhang, R Korhonen. On the Nevanlinna characteristic of f(qz) and its applications[J]. J Math Anal Appl, 2010, 369: 537-544.
[19] W K Hayman. On the characteristic of functions meromorphic in the plane and of their integrals[J]. Proc London Math Soc, 1965, 3-14A: 93 -128.
[20] Q C Zhang. Meromorphic functions sharing three values[J]. Indian J pure appl Math, 1999, 30: 667-682.
[21] Li X M, Yi H X. Uniqueness of meromorphic functions whose certain nonlinear differential polynomials share a polynomial[J]. Comput Math Appl, 2011, 62: 539-550.
UniquenessResultsConcerningDifferentialPolynomialsandq-DifferencePolynomialsofMeromorphicFunctions
LI Xiao-Min1, LIU Xue-Feng1, XU Hui-Cai2, SUN Yin-Long1
(1.School of Mathematical Sciences,Ocean University of China, Qingdao 266100, China; 2.School of Information, Renmin University of China, Beijing 100872, China)
In this paper, we study the uniqueness questions for the derivatives of certain nonlinear polynomials of meromorphic functions and their q- shifts or q-difference operators sharing a finite nonzero value, the questions are related to a question concerning differential polynomials of meromorphic functions which was posed by M. L. Fang in 2009. The results in this paper extend the corresponding results given by M. L. Fang and others.
q-difference polynomials; defferential polynomials; meromorphic functions of zero order; uniqueness theorems
O174. 52
A
1672-5174(2017)12-137-08
责任编辑 陈呈超
10.16441/j.cnki.hdxb.20140280
李效敏, 刘雪峰, 徐会彩,等. 涉及q-差分微分多项式的亚纯函数的唯一性[J].中国海洋大学学报(自然科学版),2017, 47(12): 137-144.
LI Xiao-Min, LIU Xue-Feng, XU Hui-Cai, et al.Uniqueness results concerning differential polynomials and q-difference polynomials of meromorphic functions[J].Periodical of Ocean University of China, 2017, 47(12): 137-144.
国家自然科学基金项目(11461042,11171184);山东省自然科学基金项目(ZR2014AM011);中国人民大学科学研究基金项目(16XNH117)资助
Suppoted by the National Science Foundation of China(11461042,11171184);the National Science Foundation of Shandong Province, China(ZR2014AM011);the Reseach Funds of Renmin University of China(16XNH117)
2014-09-12;
2015-05-05
李效敏(1967-),男,教授。E-mail: lixiaomin@ouc.edu.cn
AMSSubjectClassifications30D35;30D30
