基于因子分析的珠江三角洲城市竞争力的研究

王军 中船投资发展有限公司

基于因子分析的珠江三角洲城市竞争力的研究

王军 中船投资发展有限公司

本文运用因子分析的方法，科学分析了珠江三角合奏核心城市的综合竞争力状况，探讨了提升城市竞争力的对策，根据多元统计分析方法，选取能充分反映城市综合竞争力的29个指标，对珠江三角洲的九个城市2015年的统计数据进行因子分析，统计结果显示，经济总量、基础设施和产业结构是影响城市综合竞争力的三个主要因子，并且对各城市竞争力进行了综合评定，为各城市的发展提出了一些政策性建议。

因子分析 珠江三角洲 城市竞争力

一、引言

人类社会进入了经济、科技和竞争力全球化的新时代。竞争全球化不仅意味着竞争范围的全球化、竞争领域的全面化、竞争程度的激烈化，还意味着竞争主体的多层次化和竞争方式的复杂化。“国家竞争力”和“企业竞争力”曾一度被提上历史已成，随着世界城市体系的形成、扩大和调整，城市已经成为参与国家竞争的重要部分和竞争企业的载体，在国际经济中的地位越来越重要，“城市竞争力”的研究越来越多的收到学者和政策制定者的重视，普遍引用的城市竞争力的概念是：在社会、经济结构、价值观、文化、制度政策等多个因素综合作用下，创造和维持一个称呼四为其自身发展在其从属的大区域中进行资源优化配置而获得城市经济持续增长的能力。

城市竞争力的研究对于城市乃至其所属区域的发展具有十分重要的意义，客观清楚地认识自身的地位和处境、优势和不足，是制定城市科学发展战略的前提。珠江三角洲地区经济发达，城市密集，在全国具有重要的经济地位，但是，随着长江三角洲地位经济的飞跃发展，环渤海经济带的崛起，珠江三角洲面临的竞争压力越来越大，因此，在这种形势下，研究本地区城市经真理，分析城市发展的优劣势，对促进区域内城市间的优势互补，优化配置各种资源，全面提升区域经济在全国乃至世界的竞争力具有十分重要的意义。

二、因子分析法的原理

基于因子分析法进行的综合评价，亦适用于对城市社会经济发展状况的综合评价，其基本步骤如下：

假设有m个城市，n个评价指标，则矩阵X0=[Xij]m×n即为评价样本矩阵。

（1）原始矩阵的标准化。为将不同质的指标综合加总，对全部指标进行标准化（无量纲化）处理:Yij=（Xij—Xj）/dij，其中：i=1,2,3…m；j=1，2,3…n；Xij为第i 个城市的第j个指标值；Yij为第j个指标标准化后的数值；Xj为m个城市的第j个指标均值；dij为第i个城市指标的标准差。

（2）求出标准化矩阵Y的相关矩阵R；

（3）求R的特征值，并根据特征根确定特征向量；

（4）计算特征根的累计贡献率。根据累计贡献率大于85%的原则，确定主因子的个数和相应的特征向量矩阵，与此同时，计算最后综合得分的加权权数则由每个主因子的信息贡献率确定，即每个综合指标的权重由它对综合评价的共吸纳率确定，其大小取决于指标间的差异。

（5）计算主因子得分值；

（6）计算综合评价总得分值。总得分值越高，说明城市社会经济发展状况越好。

三、各城市竞争力分析评价

（一）评价指标的选取

本文所研究比较的城市综合竞争力主要是比较城市经济功能的强弱，关键是城市经济的几句和扩散功能的比较，为了定量测量和实证分析的需要，依据科学性、可比性、合理性和可操作性的原则，结合江苏各市实际情况，选取能反映城市综合竞争力的29项统计指标，建立相应的统计指标体系，具体如表1

表1 珠江三角洲城市竞争力评价指标

这29项指标分别从经济总量、质量、流量等方面反映了城市的综合竞争力。

（二）求R的特征值及贡献率

将原始数据标准化后（标准化处理后的数据从略），利用SPSS，计算得到R的特征值及贡献率如表2所示，从表2中可以看出，相关系数绝对值绝大部分大于0.3，适合做因子分析。

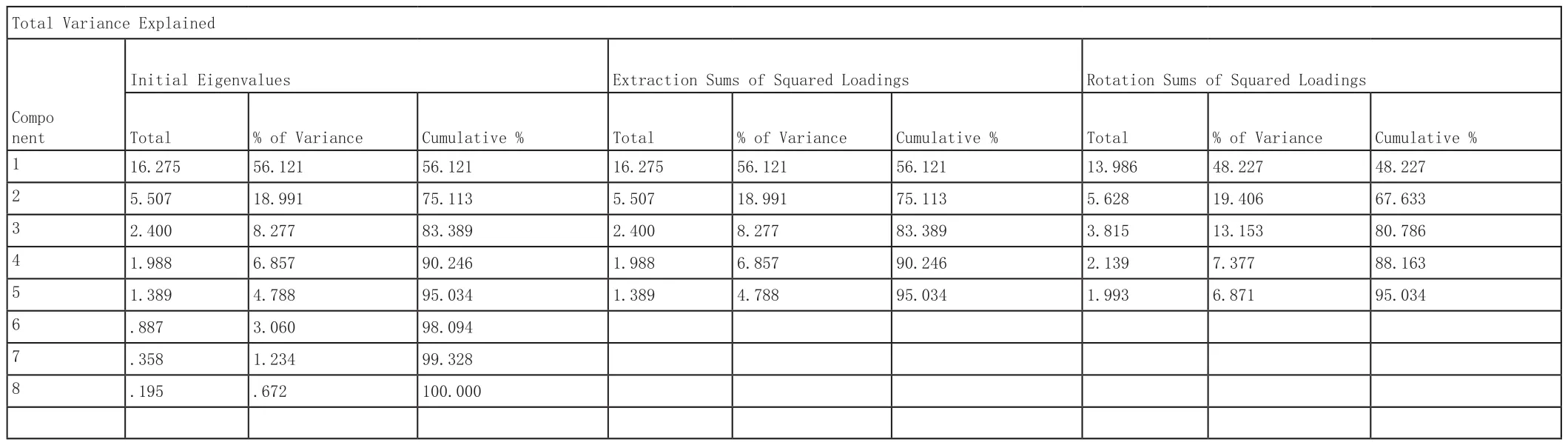
表2：R的特征值及贡献率

从表2中可以看出，变量相关系数矩阵有三大特征根：16.275，5.507，2.400，1.988，1.389，他们一起解释了变量X的标准化方差的95.034%（累积贡献率）。这样，对于此项研究的绝大部分要求，前五个主成分提供了原始数据所能表达出来的足够的信息，同时，基于构成内定特征值大于1的规则，主因子分析的过程相应提取五个主分量。

（三）建立因子载荷矩阵

对提取的五个主分量建立原始因子载荷矩阵A，同时，为便于对各因子载荷做合理解释，对其进行旋转，使其结构简化，是的每个因子的载荷的平方按列向0或者1两极分化，以起排除噪声干扰的作用，表5即为方差最大化正交旋转矩阵A。同时，表5给出的是原始数据X和主成分均已标准化处理后的前五个所提取的主成分的载荷矩阵。

由载荷矩阵可以看出，第一主成分在X1，X3，X4，X5，X6，X7，X9，X10，X11，X12，X13，X14，X15，X16，X18，X22，X26，X29上的载荷较大；第二主成分在X2，X8，X17，X23，X24，X28上的载荷较大；第三主成分在X19，X27上的载荷较大；第四主成分在X25上的载荷较大，第五主成分上在X21上的载荷较大。

表3：方差最大化正交旋转矩阵（因子载荷矩阵）

表4：各因子得分系数表

（四）因子评分

因子得分是城市综合竞争力计算的基础，根据因子得分矩阵简历因子得分函数，计算出各个市在5个公因子上的得分，如下表所示。

表5：各城市综合竞争力得分

以各因子的信息贡献率作为加重权数计算个城市的综合测评得分，公式如下：

其中，Zi为各重视社会经济发展状况得分(i=1,2,3,4……29)；Yji的系数为各因子的信息贡献率，它是各因子的方差贡献率与五个主成分的累计贡献率的比值。

通过计算，最后得分可将珠江三角洲的城市社会经济发展状况因子评分及排序如表6所示。

表6：各城市排名

从表中可以看出，广州、深圳和东莞之间的差距不大，而其他几个市之间的差距与前三个城市的差距较大，但是他们之间的差距不大，但是前三个城市与后面竞争力较弱的几个城市相比，优势又不是很突出，具体来说，珠海市的各项因子发展比较均衡，市场经济条件也相对较好，中山市是一个活力较强、市场发育较成熟的城市，但是服务能力和经济实力方面还有待提高。惠州市和江门市在珠江三角洲地区属于竞争力较弱的城市，各项因子的竞争力都有待于提高，这两个城市应该充分挖掘内外的优势资源，积极融入珠三角洲内部的深层次合作，坐到与其它城市的优势互补，接受其它城市的辐射，从而不断提升自身的综合竞争力。

四、小结

通过上述因子分析可以看出，粤北及粤西、粤东的城市竞争力相对较弱，这从总体上拉低了广东省总体水平，因此，珠江三角洲作为区域经济板块，要想在与其他经济板块竞争中保持其竞争力，需要加快转型升级，尤其是粤东西北要加快发展，这可以通过在东西两翼布局交通基础设施建设，加快其发展进程，同时，加快创新建设步伐，在当前创新引领经济发展的大背景下，需要激发这些地区的经济活力。同时，可以通过基本公共服务均等化等促进城乡协调发展，推动劳动力、资本等要素向这些地区的流动，从而确保该地区在改革创新中获得长足发展，力争将珠江三角洲城市群建设成为世界一流的城市群。