乒乓球运动员控球稳定性试验与理论研究

张俊伟，李 春，丁勤卫，任 杰，季云峰，施之皓，叶 舟

乒乓球运动员控球稳定性试验与理论研究

张俊伟1，李 春1，丁勤卫1，任 杰2，季云峰2，施之皓2，叶 舟1

积分制是很多体育项目运动员最常用的排名方式，根据运动员所参加的比赛和获得名次大致可以反映运动员综合水平排名，但此排名还受某些偶然因素影响，如比赛中关键球的运气成分，因此运动员在某段时间内发挥稳定性与其排名可能有所差异，但对于重要赛事指定哪个运动员参加，教练则要综合考虑运动员近期的发挥状态，特别是发挥稳定性。针对乒乓球运动员控球稳定性无法定量描述的问题，通过自主设计的落点采集系统试验获得6名不同水平运动员接发球的落点数据，采用数理统计和分形理论方法分别计算落点的数学期望、方差、协方差、相关系数、Hurst指数和关联维数，并提出定量评估运动员控球稳定性的参数，即关联期望率。结果表明：数理统计和分形方法中的参数均不能单独衡量运动员控球稳定性；落点的Hurst指数均介于0.5～1.0之间，具有长程正相关性，符合分形特征；提出的关联期望率能较好地衡量运动员控球稳定性，值越大说明运动员控球越稳定。研究结果为量化乒乓球运动员的控球稳定性提供了理论基础和实现途径，同时也为教练根据不同技术特点的对手指派出战队员，此外，运动员本身还可根据自己控球的关联期望率来合理训练，以提高发挥的稳定性。

乒乓球；落点；稳定性；数理统计；分形；关联期望率

速度、力量、落点、旋转和线路5大要素共同决定击球的时空特性[1-2]。学者们对乒乓球的研究大都基于5大要素，但受仪器设备和研究方法等限制，对其研究深入程度有所差异。随着试验器材的日趋先进和计算机仿真技术的快速发展，对速度、力量、旋转和线路已开展了定量研究，但因乒乓球落点数据采集系统复杂且成本较高，国内外学者对落点的试验研究相对较少。

乒乓球落点是指，球被击出后第一次与球台的接触点[3]，乒乓球落点与其他要素之间联系密切，理想的落点不仅可弥补力量不足的缺陷和增加速度快的威力，且可扩大对方移动范围、紧抓对方弱点和压制对方特长技术发挥，从而在比赛中更加主动，创造得分机会。

国内外众多学者对乒乓球开展了研究，有研究[4]根据空气动力学原理，数值求解得到乒乓球三维空间的飞行线路，且对比分析了温度和空气对飞行线路的影响；H.P.TANG等[5]采用不同击球速度和角度回击发球机发出的球，测速系统获得乒乓球在运行过程中速度减小率，旨在比较新球与旧球的碰撞过程对比赛的影响；通过录像观察和数理统计等方法，从线路、落点对马琳和马龙比赛中接发球特征与规律进行对比研究[6]；采用调查访问、试验和数理统计等方法，对新型无缝塑料乒乓球与传统赛璐珞乒乓球进行试验，比较落点准确性、击球速度和旋转等要素，为未来进一步适应新球的技战术训练和发展提供理论依据和参考[7]；将乒乓球台划分为12个区域，提出了乒乓球12区落点训练法，拓宽了传统乒乓球落点训练模式，并应用于教学试验[8-9]；采用数理统计等方法，对中国队与德国队在第47届世界乒乓球锦标赛男子团体决赛中的落点进行分析，对比得出亚洲和欧洲运动员落点有着明显差异性，对新规则下提高击球质量提出了针对性建议[10]；在新规则背景下，将球台划分为3个大区、15个小区，探索乒乓球战术训练的落点监控方法，并应用于教学试验，要求学生根据不同战术要求将球击到相应的区域，便于直观教学及击球动作的定型，在提高战术训练质量、实战能力方面优于常规方法[11]。Y.F.CHEN等[12]开发了一种由压电薄膜传感器精确定位乒乓球落点系统，并以国立虎尾科技大学的学生为研究对象。该系统可以准确检测到落点位置，显示对象的位置分布，确定对象的准确性（即平均偏差距离X轴和Y轴的中心位置）和标准偏差，在此基础上可以进一步定量分析学生击球落点的精确性和稳定性。R.G.MA和H.W.XING[13]基于落点识别设计了一套乒乓球智能训练评估系统，采用目标跟踪算法，结合滤波器箱和概率统计方法，提出了基于单目视觉的位置识别，具有时间复杂度低、精度高的优点。

由此可见，现有对乒乓球的研究大多基于速度、力量、旋转和线路。对落点开展研究的学者一方面基于这一要素提出或改进训练方法，旨在达到更加科学的训练教学，提高运动员水平，但只是定性判断训练结果，并没有检验运动员训练成绩的具体指标；另一方面，目前研究落点仅通过传统的数理统计方法，过于单一，且大多只是在球台上分区统计落点数量并进行教学与训练，存在诸多不足。传统的数理统计方法大多采用线性模拟，显然忽略了混沌时间序列由确定系统产生的非线性动力系统的本质，而是把这种时间序列归结为随机噪声。因此，采用传统的数理统计方法模拟和预测这种时间序列往往会忽略许多重要信息[14]。

为此，本文采用课题组与上海体育学院合作设计的乒乓球落点采集系统，通过试验获得精确的落点数据，采用数理统计和分形理论对比研究不同水平运动员接发球落点，旨在探寻乒乓球运动员控球稳定性参数，以期为国内外衡量运动员水平提供理论参考。

1 落点数据采集

在体育学院教师队伍中挑选一级运动员（从事乒乓球运动6年以上，平均年龄30.5岁），在学员队伍中挑选二级运动员（乒乓球学习3年以上，平均年龄22岁），在非专业运动员中挑选业余选手（球龄2年以上，平均年龄18岁），每个等级中水平有所差异，在同一等级中分别挑选较好（+）和较差（-）的运动员，即有6名运动员（业余-、业余+、二级-、二级+、一级-和一级+）参加测试，落点数据采集系统见图1。

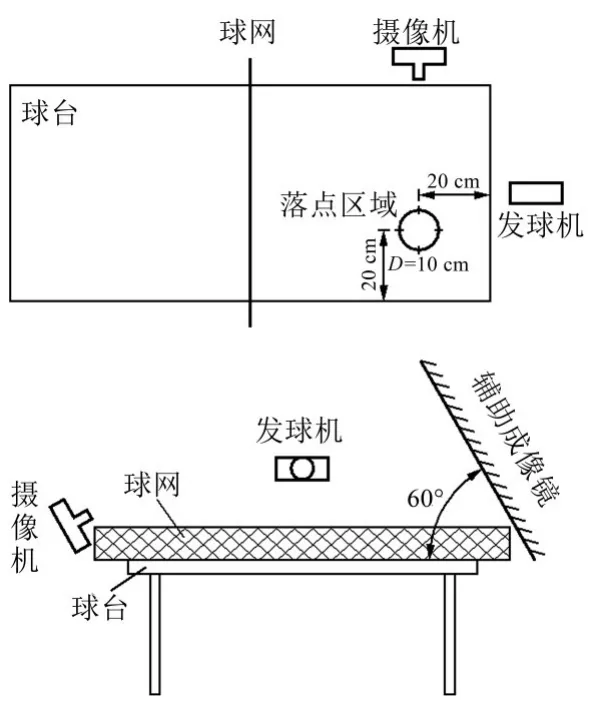
图1 乒乓球落点数据采集系统Figure1 Placement Data of Table Tennis Acquisition System

发球机型号为泰德V-989E，可发出无旋、上旋、下旋和左旋等9种球，调节范围40°，速度为4～50 m/s；高速摄像机为索尼PXW-Z150，分辨率为4 K，120帧/s；落点区域为直径为10 cm的圆，其圆心为目标落点，与球台两边缘的距离均为20 cm；辅助成像镜与球台夹角为60°。

工作原理为：发球机以15 m/s的速度发出无旋球，运动员以落点区域的圆心为目标落点接发球，待球被击回发球侧球台时，高速摄像机拍摄辅助成像镜中的图像，得到一系列接发球落点图片，找到球与桌接触时刻的图片，以落点区域的圆心为坐标原点，直径为比例尺换算为落点的实际坐标（见图2）。

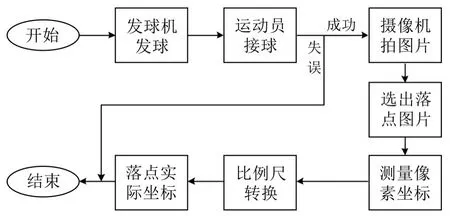
图2 落点采集系统流程图Figure 2 The Flow Chart of Placement Data Acquisition Ssystem

测试6名运动员接发球落点数见表1，实测落点坐标见图3。

表1 落点数据Table1 The Data of Placement

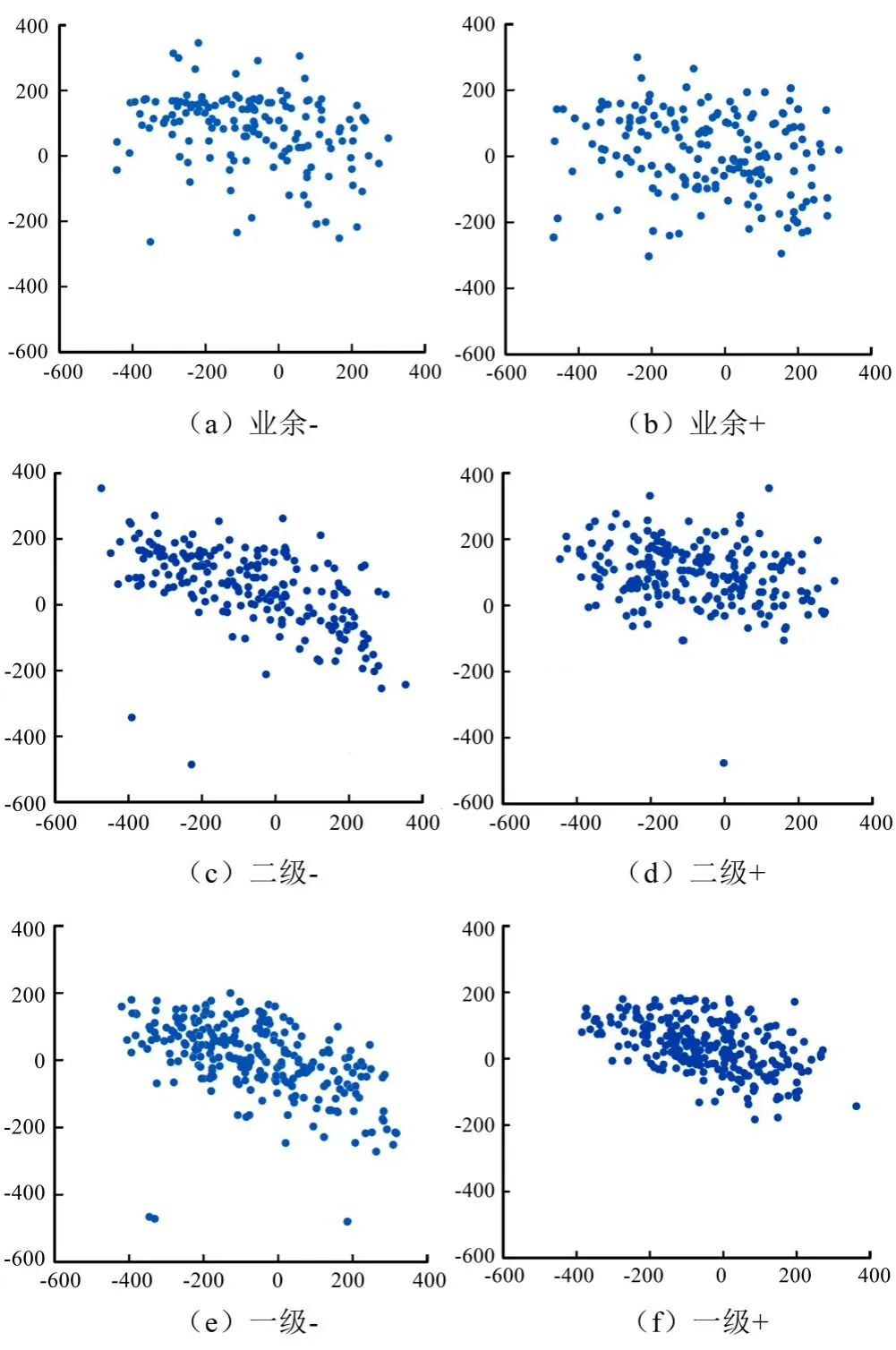
图3 不同水平运动员落点/mmFigure3 The Placement of Athletes of Different Levels/mm

2 数理统计方法

2.1 数学期望

数学期望是试验中每次可能结果的概率乘以其结果的总和的平均。它是最基本的数学特征之一，反映随机变量平均取值的大小。

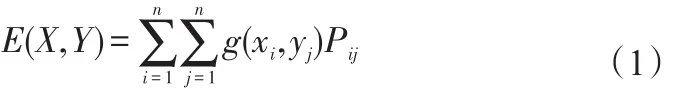
2.2 方差

方差是各数据分别与其数学期望之差的和的平均数，它是衡量数据离散程度的参数，用来度量数据和其数学期望之间的偏离程度。

式中：E(X)和E(Y)分别为分量X和Y的数学期望。

2.3 协方差

协方差用于衡量2个变量的总体误差。若分量X与Y相互独立，则二者的协方差为0，这2个变量称为不相关的，因此协方差是描述变量关系的统计参数。

对于协方差，常采用以下公式计算：

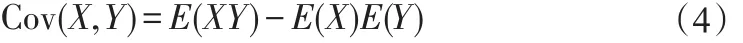
2.4 相关系数

协方差和相关系数均是描述X和Y之间相互关系的参数。相关系数是用以反映变量间相关关系密切程度的统计指标。

式中：σ(X)和σ(Y)分别为X，Y的均方差；ρXY＞0时，变量X和Y正相关；ρXY＜0时，变量X和Y负相关；ρXY=0时，则变量X和Y不相关。

3 分形理论与关联维数

3.1 分形理论

非线性科学是一门研究非线性现象的革命性基础科学，被誉为20世纪自然科学中的“三大革命之一”，与量子力学和相对论具有相同的地位[15]。

分形理论是非线性科学研究中十分活跃的一个分支[16]，可理解为局部和整体在某方面存在相似性，其数学基础是分形几何[17]。20世纪70年代中期，由MANDELBROT创立以来，分形理论无论是在数学基础还是在应用方面都得到快速发展[18]。分形维数是定量描述分形系统的重要参数，它是用来衡量一个几何集成或自然物体不规则和复杂程度的数[19]。常用的分形维数包括自相似维数、盒维数、信息维数、关联维数、广义维数和Lyapunov维数等[20]。其中，关联维数能定量描述吸引子的几何特征，对吸引子不均匀性反应敏感，能很好地反映吸引子动态结构[21]。

3.2 分形特征验证

3.2.1 重标极差分析法 1951年，英国著名水文学家H.E.HURST提出重标极差分析法（Rescaled Range Analysis，R/S分析法）[22]。B.B.MANDELBROT和J.R.WALLIS[23]在理论上证实了此方法的准确性，且同A.BENASSI等[24]对其进行了补充和完善。R/S分析法基本思想表达为：

通过最小二乘法得到散点的拟合直线，该直线的斜率即为Hurst指数。

3.2.2 Hurst指数判定依据 R/S分析属于非参数分析，特点是无需对数据序列做分布假定[25]。Hurst指数意义如下：（1）H＝0.5时，序列为独立同分布的随机序列，变量之间是相互独立的，相应的相关系数为零，现在不会影响未来；（2）0≤H＜0.5时，时间序列表现为一种反持续性，变量之间是负相关的；（3）0.5＜H≤1.0时，时间序列具有状态持续性，存在长程相关性，表现为分形时间序列。从理论上讲，现有的变化将对后续变化产生持续影响。

3.3 关联维数

3.3.1 相空间重构 N.H.PACKARD等[26]认为，从一个变量的时间序列可以重构出此变量的动力学系统的相空间。F.TAKENS[27]和R.MAÑÉ[28]从理论上进一步证明了N.H.PACKARD的观点，并提出了相空间维数的下界m≥2D+1。相空间重构理论的建立为混沌时间序列的预测奠定了坚实的理论基础[21]。

1980年，N.H.PACKARD等[26]提出了2种相空间重构方法：坐标延迟法和导数重构法。导数重构法中数值微分的计算对误差较敏感，因此选取坐标延迟法重构相空间如下：对落点时间序列x（ti）（i=1，2，…，n），将其延拓为m维相空间的相形分布，其中相点为共 有N-(m-1)τ个相点。式中：m为嵌入维数，即重构相空间的最小维数（整数）；τ为延迟时间。为了能在重构的相空间中刻画原系统的性质，需合理确定m和τ。

（1）嵌入维数m的确定。在实际求取嵌入维数时，取值太小，则可能引起吸引子折叠导致发生自相交，相交区域内的小领域内可能会包括不同部分吸引子的点；理论上，嵌入维数偏大是可行的，但实际上会增加吸引子几何不变量的计算工作量。常用的嵌入维数的选取方法包括伪最近邻法[29]、Cao方法[30]和偶几何法[31]等。

（2）延迟时间τ的确定。延迟时间太小，无法提供2个独立的坐标分量；延迟时间太大，则2坐标在统计意义上又是完全独立的。延迟时间计算方法包括自相关法[32]、平均位移法[32]和互信息法[33]等。

（3）考虑到以上求取最佳嵌入维数（延迟时间）的方法都需要先确定最佳延迟时间（嵌入维数），即把嵌入维数和延迟时间分开考虑存在不足。1999年，H.S.KIM等[34]提出了同时求取这2个参数的C-C法，同时证明嵌入维数和延迟时间在整体上存在乘积关系；2003年，M.B.ATAEI等[35]进一步证明了二者不是相互独立的，故采用C-C法确定嵌入维数和延迟时间。

3.3.2 G-P算法 在相空间重构基础上，P.GRASSBERGER和I.PROCACCIA[36]提出了基于时间序列直接计算关联维数的G-P算法。设有2个相点：

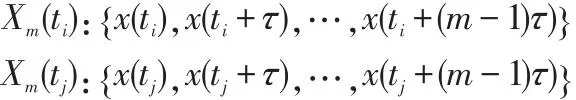
其欧氏距离εij为：

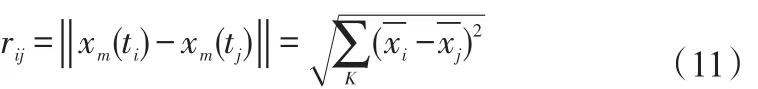
给定一个距离r，检验rij有多少落在以r为半径的圆内，即：

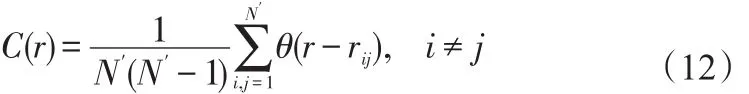
式中：N′=N-(m-1)r，且θ是Heaviside函数，即：

数据管理、预警管理与预警发布管理3个模块安装在服务器端，由于交互性较强，采用B/S架构，基于ASP.NET的MVC模式设计。预警分析引擎也安装在服务器端，由于不需要进行详细的配置，采用C/S架构。服务器端实现远程数据管理、预警规则设定、预警分析处理等功能，在接收到实时数据后，进行分析计算，判别是否超警，同时生成预警消息，推送至客户端。

适当选取r，存在如下关系：

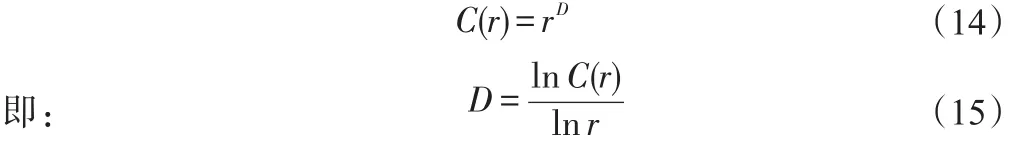
式中：D为关联维数。

G-P算法流程图见图4。

图4 G-P算法流程图Figure4 Flow Chart of G-P Algorithm

4 结果与分析

4.1 数理统计分析

通过课题组与上海体育学院合作设计的乒乓球落点数据采集系统，获得6名不同水平运动员接发球落点数据，采用数理统计方法计算其数学期望、方差、协方差和相关系数。

二维离散型变量的数学期望是描述各个落点到目标落点之间距离的加权平均值，与落点的联合概率分布有关。一般而言，运动员水平越高，接发球落点的数学期望越小。数据表明：6名不同水平运动员接发球落点的数学期望总体符合运动员水平越高，其值越小的规律；业余+的数学期望比二级-稍小，是因为二级-的联合概率分布不如业余+集中，且有几个落点远远偏离目标落点，致使其数学期望略大于业余+（见表2，图5（a））。

方差是数据与数学期望相差的度量值，用来衡量数据的离散程度，与分量X和Y的平均值有关。6名运动员落点的方差曲线并未呈现规律性，不能衡量乒乓球运动员控球稳定性（图5（b））。

协方差和相关系数都是描述X和Y之间相互关系的参数。协方差衡量2个变量的总体误差；相关系数反映变量间关系密切程度。6名运动员落点的协方差和相关系数均不为零，说明落点分量X和Y之间不是相互独立的，不能分开单独研究。6名运动员落点的协方差和相关系数也无法体现出规律，故无法衡量运动员控球稳定性（见图5（c），图5（d））。

表2 落点统计参数Table2 The Statistical Parameters of Placement

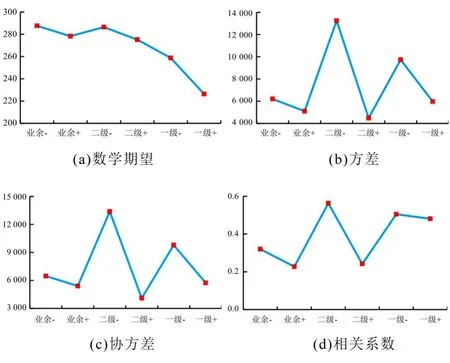
图5 落点统计参数曲线图Figure5 The Statistical Parametric Curves of Placement

4.2 分形理论分析

4.2.1 Hurst指数 6名运动员接发球落点的Hurst指数均介于0.5～1.0，落点时间序列具有状态持续性，存在长程相关性，符合分形特征，且Hurst指数越接近1.0，序列的持续性程度就越强，反之越弱（见表3）。

表3 落点的Hurst指数Table3 The Hurst Exponent of Placement

4.2.2 关联维数 关联维数计算过程首先采用坐标延迟法对落点时间序列进行相空间重构，此过程考虑到数理统计方法未能涉及的落点顺序问题，能反映数理统计方法不能表达出的内在信息。在相空间重构基础上，采用G-P算法计算不同嵌入维数下双对数ln(Cr)-ln(r)曲线。

随着嵌入维数从2增加到最佳嵌入维数12，6名运动员落点的双对数ln(Cr)-ln(r)曲线斜率逐渐增大，直到最佳嵌入维数趋于稳定，此时斜率为关联维数D（见图6）。关联维数随嵌入维数变化曲线见图7，6名运动员接发球落点的关联维数见表4。

本研究虽然符合运动员水平越高，关联维数越大的趋势，但关联维数描述的只是落点与落点之间的规律，与所选目标落点无关，如相同的一组落点在靠近和远离目标落点时，二者关联维数是相等的。不失一般性，仅关联维数亦不能描述运动员接发球控球稳定性。

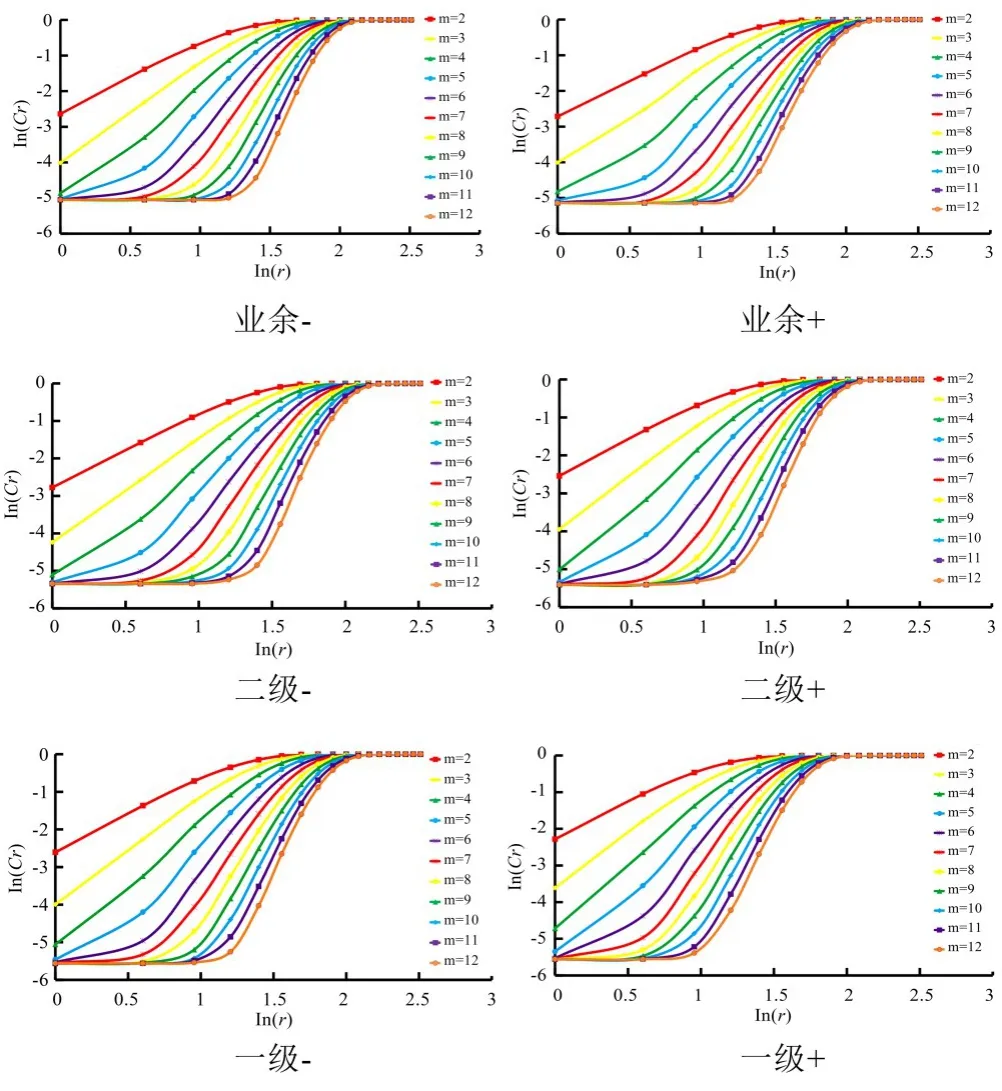
图6 不同嵌入维数下双对数lnC(r)-lnr散点图Figure6 Double Logarithmic Scatter Plotln(Cr)-ln(r)With Different Embedding Dimension

图7 嵌入维数m与关联维数D关系曲线Figure7 Curve Between Embedding Dimension m and Correlation Dimension D

表4 落点的关联维数DTable 4 Correlation Dimension D of the Placement

4.2.3 关联期望率 结合关联维数和数理统计方法中数学参数，反映运动员接发球控球稳定性。为解决关联维数不能区分相同的一组落点在靠近和远离目标落点时二者关联维数是相等的问题，在数理统计参数中发现数学期望能很好地描述落点偏离目标点远近问题，尝试找出关联维数和数学期望之间的关系来描述运动员接发球控球稳定性。一般而言，运动员控球稳定性越好，其关联维数越大，数学期望越小，故定义关联期望率σ为关联维数D与数学期望E之比：

式中：D为落点的关联维数；E(X,Y)为落点的数学期望。

数据表明，随着运动员水平越高，其关联期望率σ越大，控球稳定性越好（见表5，图8）。

表5 落点的关联期望率（×10-2）Table5 The Rate of Correlation Dimension and Mathematical Expectation of Placement（×10-2）

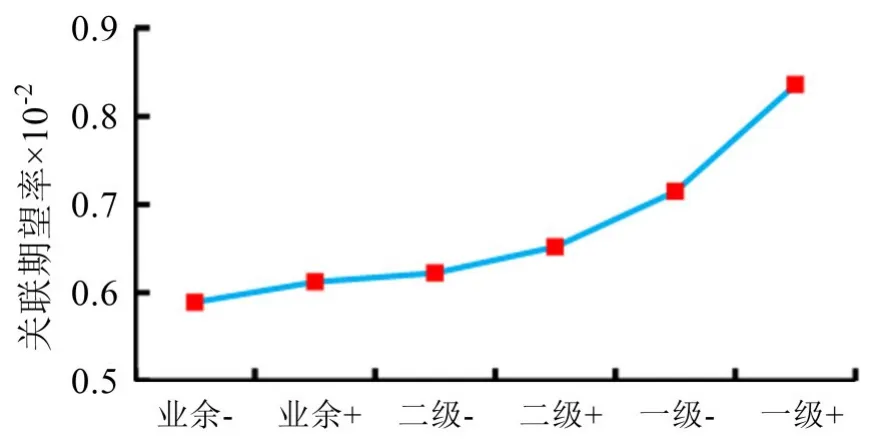
图8 落点的关联期望率曲线图Figure8 The Curve of the Rate of Correlation Dimension and Mathematical Expectation of Placement

5 结论与建议

5.1 结论

本文通过试验测得6名不同水平乒乓球运动员接发球落点数据，采用数理统计和分形方法分别计算各组落点的数学期望、方差、协方差、关联维数、Hurst指数和关联维数，结论：（1）传统数理统计方法视乒乓球落点数据为随机的，单独的统计参数不足以衡量运动员控球稳定性；（2）分形方法中的关联维数也不能单独用于衡量运动员控球稳定性；（3）落点的Hurst指数均介于0.5～1.0之间，具有长程正相关性，符合分形特征；（4）关联期望率（关联维数与数学期望之比）能较好地反映运动员控球稳定性，其值越大说明运动员控球越稳定。

5.2 建议

目前，乒乓球世界排名采用的是积分制，虽能大致反映运动员综合水平排名，但此排名还受某些偶然因素影响，如运动员因伤病不能参加比赛，决赛中关键球的运气成分，因此运动员发挥稳定性与世界排名可能不一致。文中提出的关联期望率能较好地反映运动员控球稳定性，在团体赛中可根据不同技术特点的对手教练指派出战队员。此外，运动员本身还可根据自己控球的关联期望率来合理训练，以提高发挥的稳定性。

[1]詹英，吴志刚，李博.乒乓球教学与训练[M].哈尔滨：东北林业大学出版社，2009：21.

[2]贾纯良，穆亚楠.乒乓球快速入门与实战技术[M].成都：成都时代出版社，2014：20.

[3]彭跃清，陈利和.乒乓球入门技巧一月通[M].北京：北京理工大学出版社，2014：43.

[4]余万，李春，朱玲，等.不同比赛气候条件对乒乓球飞行轨迹影响研究[J].运动，2016，138（10）：23-24.

[5]TANG H P，MIZOGUCHI M，TOYOSHIMA S.Hitting properties of the new 40mm diameter table tennis ball[J].Research of Physical Educa⁃tion，2002，47（2）：155-162.

[6]邱团，李超，陈础.中国乒乓球主力运动员马琳与马龙接发球技战术比较研究[J].中国体育科技，2010，46（5）：52-55.

[7]成波锦，杨欢.新型无缝塑料乒乓球的特征及对击球速度和旋转影响的试验研究[J].北京体育大学学报，2014，37（10）：141-144.

[8]陈德林.乒乓球12区落点训练法[J].中国学校体育，1993（1）：57.

[9]陈德林.乒乓球12区落点训练法的试验研究[J].体育科学，2000，20（4）：74-76.

[10]张秋芬.第47届世界乒乓球锦标赛男子团体决赛击球落点分析[J].中国体育科技，2004，40（6）：64-66.

[11]陈德林.乒乓球战术训练的落点监控与效果评定[J].广州体育学院学报，2006，26（5）：56-57.

[12]CHEN Y F，LIU C H，FANG T H，et al.A study of applying piezoelec⁃tric material to hitting placement sensing system for table tennis players[J].Sensor Letters，2012，10（5）：1173-1177.

[13]MA R G，XING H W.Table tennis training intelligent assessment sys⁃tem based on placement identification[J].Applied Mechanics&Materi⁃als，2013，440（10）：341-345.

[14]刘式达.物理学中的分形[M].北京：北京大学出版社，2014：210.

[15]郝柏林.分岔、混沌、奇怪吸引子、湍流及其他：关于确定论系统中的内在随机性[J].物理学进展，1983（3）：63-150.

[16]王汉斌.煤与瓦斯突出的分形预测理论及应用[M].北京：煤炭工业出版社，2012：01.

[17]刘延柱，陈立群.非线性动力学[M].上海：上海交通大学出版社，2000：8.

[18]RINALDO A，RODRIGUEZITURBE I I，RIGON R，et al.Self-orga⁃nized fractal river networks[J].Physical Review Letters，1993，70（6）：822-825.

[19]曼德尔布洛特.分形对象[M].北京：世界图书出版公司，1999：17.

[20]郝研.分形维数特性分析及故障诊断分形方法研究[D].天津：天津大学，2012.

[21]乔美英.工作面瓦斯涌出量时序混沌分形特性分析及其预测研究[D].徐州：中国矿业大学，2012.

[22]HURST H E.Long term storage capacity of reservoirs[J].Transactions of the American Society of Civil Engineers，1951，116（12）：76-808.

[23]MANDELBROT B B，WALLIS J R.Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence[J].Water Resources Research，1969，5（5）：967-988.

[24]BENASSI A，BERTRAND P，COHEN S，et al.Identification of theHurst index of a step fractional brownian motion[J].Statistical Inference for Stochastic Processes，2000，3（1）：101-111.

[25]MANDELBROT B B，NESS J W V.Fractional brownian motions，frac⁃tional noises and applications[J].Siam Review，2015，2015（4）：1-2.

[26]PACKARD N H，CRUTCHFIELD J P，FARMER J D，et al.Geometry from a time series[J].Physical Review Letters，1980，45（9）：712-716.

[27]TAKENS F.Detecting strange attractors in turbulence[M].Springer Ber⁃lin Heidelberg：Dynamical Systems and Turbulence，1981：366-381.

[28]MAÑÉ R.On the dimension of the compact invariant sets of certain non⁃linear maps[M].Springer Berlin Heidelberg：Dynamical Systems and Turbulence，1981：230-242.

[29]王海燕，卢山.非线性时间序列分析及其应用[M].北京：科学出版社，2006：19-21.

[30]CAO L.Practical method for determining the minimum embedding di⁃mension of a scalar time series[J].Physica D Nonlinear Phenomena，1997，110（1-2）：43-50.

[31]LEI M，WANG Z，FENG Z.A method of embedding dimension estima⁃tion based on symplectic geometry[J].Physics Letters A，2002，303（2-3）：179-189.

[32]GRASSBERGER P，PROCACCIA I.Measuring the strangeness of strange attractors[J].Physica D Nonlinear Phenomena，1983，9（12）：189-208.

[33]FRASER A M，SWINNEY H L.Independent coordinates for strange at⁃tractors from mutual information[J].Physical Review A，1986，32（2）：1134-1140.

[34 KIM H S，EYKHOLT R，SALAS J D.Nonlinear dynamics，delay times，and embedding windows[J].Physica D Nonlinear Phenomena，1999，127（1-2）：48-60.

[35]ATAEI M，LOHMANN B，KHAKI-SEDIGH A，et al.Model based method for determining the minimum embedding dimension from cha⁃otic time series-univariate and multivariate cases[J].Nonlinear Phe⁃nom Complex Syst，2003，6（4）：842-851.

[36]GRASSBERGER P，PROCACCIA I.Characterization of strange attrac⁃tors[J].Physical Review Letters，1983，50（5）：346-349.

Experiment and Theoretical Research on the Stability of Table Tennis Players

ZHANG Junwei1，LI Chun1，DING Qinwei1，REN Jie2，JI Yunfeng2，SHI Zhihao2，YE Zhou1
（1.School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China；2.China Table Tennis College，Shanghai University of Sport，Shanghai 200438，China）

Point redemption scheme is the most commonly used ranking method for many sports athletes.It is based on athletes participating in the competi⁃tion and get ranked，roughly reflects the overall level of athletes ranking，but this ranking is also affected by some accidental factors，such as the key ball in the game of luck.The athletes in a certain period of time play stability and may be different for ranking，but the important events which sent athletes to the prob⁃lem，coach need to consider the athletes play recently，especially its stability.Focus on the problem of cannot quantitative describe the stability of table tennis athletes，the placement data of 6 different level athletes obtained through the experiment by the placement acquisition system designed by ourselves，then，mathematical expectation，variance，covariance，correlation coefficient，Hurst exponent and correlation dimension calculated by using mathematical statistics and fractal methods，a parameter for quantitative evaluating the stability of the athletes is put forward-the rate of correlation dimension and mathematical ex⁃pectation.The results showed that the parameters of mathematical statistics and fractal method cannot measure the stability of athletes separately.The Hurst exponent of placement is between 0.5～1.0，which has a long range positive correlation，and with fractal characteristics.The rate of correlation dimension and mathematical expectation be put forward can describe the stability of athletes，the greater of the rate of correlation dimension and mathematical expectation，the more stable of the athletes.The research results provide a theoretical basis and a way to quantify the stability of table tennis athletes.At the same time，it also assigns players for the opponent according to different technical characteristics.In addition，the athlete can also train himself according to the expectation rate of the ball control，so as to improve the stability of play.

table tennis；placement；stability；mathematical statistics；fractal；rate of correlation dimension and mathematical expectation

G 846

A

1005-0000（2017）02-117-06

10.13297/j.cnki.issn1005-0000.2017.02.005

2017-01-05；

2017-03-15；录用日期：2017-03-16

国家自然科学基金项目（项目编号：51676131；51176129）

张俊伟（1993-），男，江西乐平人，在读硕士研究生，研究方向为分形学与体育应用。

1.上海理工大学能源与动力工程学院，上海200093；2.上海体育学院中国乒乓球学院，上海200438。