追寻生长的数学课堂
2017-10-31金菊仁
金菊仁
【摘要】生长的数学课堂不仅是数学知识的教学,更要有数学思考的教学。每个学生都跟种子一样,能自己发育,自己成长。若要学生茁壮地成长,就要给他生长的力量,让数学课堂充满生长的活力。本文以《面积的认识》为例,从三方面阐述“生长”的观点:(1)找准知识的生长点;(2)不能囿于一节课的知识,更要关注后续学习的持续发展;(3)选择的学习素材不仅要“精”,而且重“联”。
【关键词】生长种子课四基数学思考
叶圣陶先生指出:“受教育的人的确跟种子一样,全都是有生命力的,能自己发育,自己成长的;给他们充分的合适的条件,他们就能成为有用之才。”俞正强老师提出:“种子课,给知识以生长的力量。”反思平时的课堂,确实过于注重要教给学生什么知识,学生要掌握什么知识,而太少在意学生学习的后续发展。若要“种子”发芽、茁壮地成长,就要给他生长的力量。如何让数学课堂充盈生长的力量呢下面以“面积的认识”为例略表想法。
一、“生长的课堂”要找准知识的生长点
所谓知识的“生长点”,是指知识的固着点,就是我们已经具备的相关知识(即已经知道了什么),是学习新知识的前提和基础,也是原有认知结构中影响新知学习的最关键的因素。我们都知道,新知容易被遗忘而还原为旧知识。只要找准并抓住知识的生长点,就能找到新知的源头活水;只要搞清楚新知是如何从旧知识生长而来的生长机制,即使新知识忘记了,学生仍会将新知识生长出来。
一节课中,如果没有找准知识的生长点,再多的素材也是画蛇添足而已,模模糊糊一大片。如果找准了知识的生长点,简简单单的素材却能取得“四两拨千斤”的效果,清清楚楚一条线。
【片段1】引入:比一比,说一说。
师:你看到了什么比一比。
生:比了铅笔的长短,红铅笔比绿铅笔长。
师:你又看到了什么比一比。
生:黑板比电视机大。
师:这次比的是什么
生:黑板面和电视机屏幕面的大小。
师:边框围起来里面的大小就是黑板的大小,也就是黑板的面积。听过面积吗
师:生活中还有哪些面吗
【思考】大多数教科书都这样定义:“物体表面或封闭图形的大小就是它们的面积。”张奠宙教授指出:“这种粗体字的所谓定义只是常识性的叙述而已,并不能帮助学生真正理解面积概念。许多教案围绕这句话进行教学设计,反复讨论什么是表面、什么是封闭,其实意义不大。面积和长度一样,也是人与生俱来的直觉。早在婴儿阶段,人们就已经能辨别两块饼的大小。把‘大小作为面积,就如把‘长短作为长度一样,并没有实质性的解惑,都是同一个意思的简单重复。”的确如此,反思之前的教学,总是围着“面积”这个概念绕圈子,花了很长时间让学生摸一摸、涂一涂各种物体的表面,活动似乎很丰富,却不知那只是一种没有生长的重复。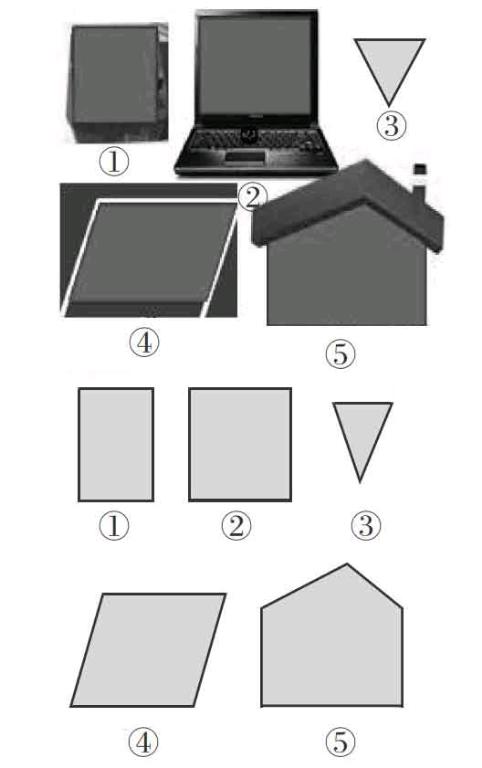
片段1中問题指向非常简洁明确,直击知识的生长点——比长短和比大小。通过两组实物图的比较,唤起学生已有的知识经验,初步感知面积就是我们所说的“面的大小”,让学生一目了然地感受到面积与长度的区别——铅笔是比长短,黑板面和电视机面是比大小,这恰是学生学习的难点(周长和面积易混淆)。让学生在比较中复习比长短的旧知识点,又生长了比大小的新知识点,自然地把“生活语言”提炼成“数学概念”——“边框围起来里面的大小就是黑板的大小,也就是黑板的面积”,真是“得来全不费工夫”。“听说过面积吗生活中还有哪些面”紧接着从长方体的相对面、圆柱的侧面曲面等不同角度来理解面积的意义,真是“一波未落一波又起,课继续”。
二、“生长的课堂”不能囿于一节课的知识,更要关注后续学习的持续发展
“面积的认识”是一节“种子课”,是为以后学习平面图形的面积和立体图形的表面积而奠定基础的一节非常重要的“生根课”。新课标提出的“四基”指的是基础知识、基本技能、基本思想、基本活动经验。前两基是显性的,可考试,可讲解,可识记;后两基是隐性的,不可考,需要体验,需要感悟。一节课怎么上出厚度来,就是要上出后面的隐性部分——基本思想和基本经验,以实现知识的正生长。以下片段便是一个很好的诠释。
【片段2】“从相对面、侧面、曲面等维度深刻理解面积的意义和以面量面的方法”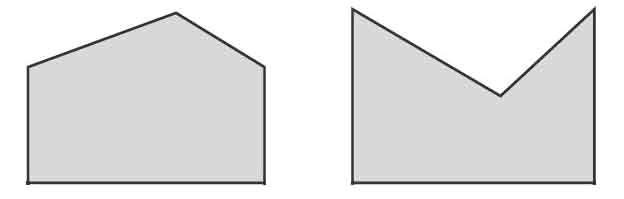
师:生活中还有哪些面吗
生:牙膏盒的面。
师追问:哪个面跟这个面的大小相等
师:杯子有面吗这是杯子底面的面积,这是杯子上面的面积,这是杯子的一个侧面,它是一个曲面,打开后会是一个什么形状呢
师:生活中的物体都有面,如果把这些物体的表面描下来,就可能是这样的一些平面图形。这些图形的面在哪里
生:外框内部的大小就是面积。
师:这些图形的面积你会涂吗(学生涂)
师:把⑤变魔术,你发现什么
生:面积变小了,周长一样。
师:有些图形周长没变,而面积变了。现在,你知道什么是面积吗
师:像课桌面的大小,就是课桌面的面积。要想知道课桌面的面积到底有多大,我们可以用什么去比一比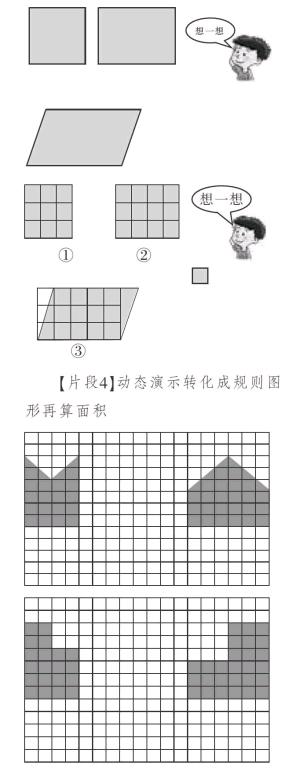
师:你估计桌面的面积大约有几个数学书封面那么大还可以用什么来摆endprint
板书:4个数学书封面,40个魔方的面,32个盒子的面,10个米粉盒子的面。
师:你们的桌面大小不一样吗为什么量的结果不一样
师:看来要用相同的标准去测量。
【思考】此处演绎得可谓淋漓尽致,越出一贯面积教学的界限,“面积”向“表面积”的扩展,把面积的意义诠释得更加深刻。第一个亮点是:本节课比较面的大小,一般选择的素材都是有大有小的面,而这里引进了相对面相等的素材,上面和下面相等,左面和右面相等,前面和后面相等,为以后长方体的表面积学习奠定了基础——让知识“生根”。第二个亮点是涉及圆柱的侧面是一个曲面,打开后是一个长方形,渗透化曲为直的思想——让思想“发芽”,把“面”的内涵解释得更为宽泛。真所谓“横看成岭侧成峰,远近高低各不同”。
另外,把5号图形变魔术,周长不变,面积变了,渗透了“等长变形”的数学思想。让学生用自己带的物体去量课桌面不仅是进一步理解“面”的含义,而且渗透了“以面量面”的重要思想方法,同时又自然地引出了统一面积单位的重要性。
三、“生长的课堂”选择的学习素材不仅要“精”,而且重“联”
这里的“联”不仅仅指本节课前后知识间的“联”,还指纵向知识体系间的“联”。“面积的认识”这节课打破过去的单一教学,把长方形、正方形、平行四边形、组合图形、圆柱形等素材有机联系起来,并且把例题中的①②④素材进行“一材多用”,让学生学会用小正方形如何测量它们的面积,孕伏长方形、平行四边形的面积测量方法。这样才能促进面积知识的旺盛生长,实现能力的多向迁移,让教学走得更远。
【片段3】先估后量(渗透三种图形的面积计算方法)
师:现在我们就用小正方形来估一估、比一比这三个图形的面积,看看这些图形里面大约能摆几个这样的小正方形
【片段4】“动态演示转化成规则图形再算面积”
【思考】张奠宙教授指出:“面积的教学,其核心是如何测量图形的大小,即如何给平面上的封闭图形一个恰当的数,能满足那三条基本性质。我们用数方格的办法给长和宽都是自然数的长方形指定了相应的面积(求出面积)。数方格的过程,蕴含了面积的有限可加性。此后,还要‘求平行四边形的面积,那里要把一个三角形切下来、搬过去凑成长方形,这是利用了面积的运动不变性。”
因此,本节课的练习不能仅仅停留在简单的数方格(数面积),而是让学生思考在图形中怎样摆小正方形(怎样测量),渗透长方形、平行四边形的面积计算公式推导过程的雏形。片段3课件的动态演示恰到好处,每种图形都先呈现一行的个数,再呈现行数,充分展示知识的形成过程,然后运用乘法意义计算出小正方形的总个数(图形的面积)。初步展示了三种图形的面积测量過程,即三种图形的计算方法(借助方格背景来计数正方形、长方形、平行四边形三种图形所含面积单位个数是探索三种图形计算方法的基础)。同时恰到好处地沟通了三种图形的联系,无痕地渗透了转化的思想。真是“润物细无声”!
再看片段4,紧接⑤号图形,进一步让学生了解组合图形的计算方法,充分运用了课件动态演示的优势,把不规则图形转化成规则图形,又一次渗透了“转化”“等积变形”等数学思想,让学生从多方面、深层次地理解面积的内涵。把整节课的素材巧妙、有机地联系起来,一环扣一环,一步生长一个知识点,凸显了本节课作为一节种子课的茂盛生长的力量。
生长的数学课堂不仅是数学知识的教学,更要有数学思考的教学。如果没有数学思考的教学,数学学习就显得比较单薄。“教学有法,教无定法”,我们一定要整体把握一个知识块的前生今世及后延,关注学生的可持续发展,让数学课堂充满生长的力量。
参考文献:
[1]张奠宙.深入浅出,平易近人——怎样测量长度、面积和体积.小学教学(数学版).2014(10).
[2]俞正强.种子课:一个数学特级教师的思与行[M].北京:教育科学出版社,2013(5).endprint
