基于学生认知水平的有效教学
2017-10-31李国良
李国良
“分数的简单应用”是人教版数学(2014)新增的学习素材,它是在学生学习分数的初步认识和分数的简单计算后的内容。用两个课时完成此教学:第一课时是通过剪、涂、摆等教学活动,让学生体会到把一些物体进行平均分,其中的1份或几份如何用分数来表示,明确部分与整体的关系;第二课时是从分数的意义入手,在操作与观察中知道求一个数的几分之几可以用整数除法和乘法知识来解决。
笔者仔细分析了教材内容,发现例1主要是从一个物体认识分数拓展到一些物体认识分数,它是学习例2的基础与起点。但对刚接触分数的三年级学生来说在认知上是否存在着一定的困难存在着怎样的困难笔者觉得有必要对学生进行一次学前调查,找准教学的起点及认知的困惑点,以期达到事半功倍的教学效果。
一、教学前测的思考
教学前测是指在学习新知前的一段时间里,通过书面、访谈、问卷等调查方式对学生进行相关知识储备和相关方法的预先测试,然后进行有针对性的分析并设计教学活动,提出相应的课堂教学策略。
1.教材的比较与分析
为使前测内容更加符合学生的认知规律,更好地反映教材的特点,笔者翻阅了北师大版、苏教版、浙教版等相关教材,发现这三套教材在安排这一内容时结构上与人教版基本一致,但呈现的顺序、内容上有一定的区别(具体见下表)。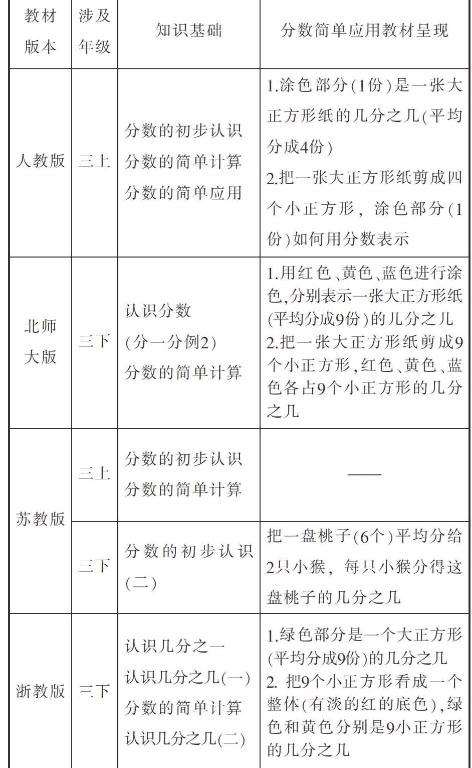
从上表中我们发现:“分数的简单应用”在年级安排上,除人教版安排在三上年级,其他均安排在三下年级;在内容结构上,北师大版直接安排在分数的初步认识里,中间没有安排分数的简单计算,其他版本均不是从一个物体直接过渡到一个整体;在内容呈现上,除苏教版外,其他是以一个大正方形剪开呈现4个或9个小正方形,来学习一份(几份)占一个整体的几分之一(几),苏教版和浙教版有盘子或淡淡的底色把一些物体看作一个整体。
2.内容的确定与思考
对四个版本的教材进行比较后,我们能清楚地发现教材要让学生掌握的内容和要点,于是拟定了三个大题6个小题作为前测的内容(如下表):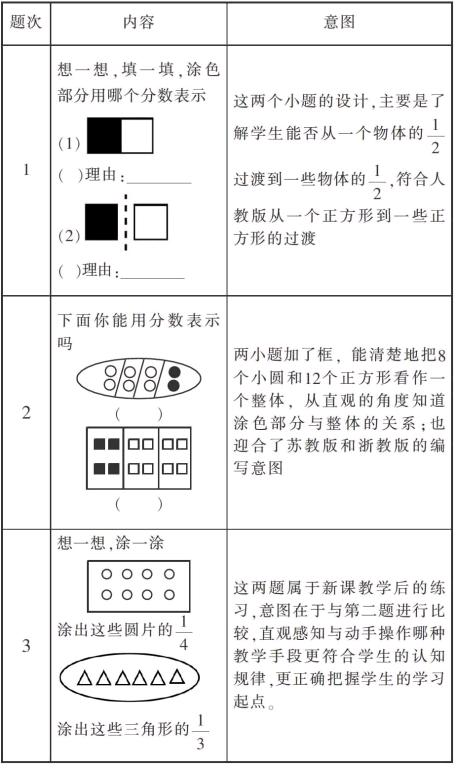
这两题属于新课教学后的练习,意图在于与第二题进行比较,直观感知与动手操作哪种教学手段更能符合学生的认知规律,也能更正确把握学生的学习起点。
这三题调查的主要目的是:通过观察、动手实践、对比分析等学习手段,了解学生从一个物体认识分数到一个整体认识分数的前概念情况,明确学生是否能运用集合中的部分元素与整个集合的关系也可以用分数来表示了解程度,便于在教学中能正确、有效地把握学习起点,达到事半功倍的效果。
二、前测结果的分析
为使本次调查更具广泛性与代表性,笔者选择了城区学校和所属乡镇中心小学三年级各2个班共164名学生进行,要求10分钟内独立完成,检测后统计结果如下表: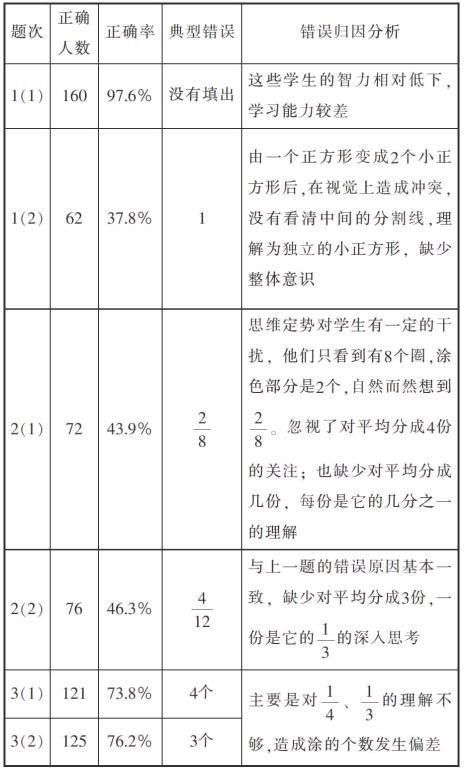
对绝大部分学生来说已不存在认知上的困难;而第2小题错误率高达62.2%,显然学生不能把两个正方形看作一个整体来理解,这一知识点应该作为本节课的重点和难点。第二题两个小题是把一些圆和一些小正方形看作一个整体,涂色部分用合适的分数来表示,它们的错误率也较高,但与第一题的第2小题相比正确率有所提高,说明了在一些图形的外面加一个圈(框)对正确理解一个整体有一定帮助,在实际教学中有必要借助这一素材。这也印证了苏教版、浙教版采用一个盘子和一个淡淡底色的道理。第三题两个小題虽然属于应用性的题目,但它们的正确率明显比第二题高,这种“倒置”现象的出现也有着其原因:一些物体平均分成若干份,得到每份是几个,可以用物体个数除以份数得到每份数。很多学生并不是把它们看作一个整体来进行平均分,一份是整体的几分之一,由此,学生的大脑中还不能把部分与整体进行有效沟通,也就是部分占整体的几分之一(几)还是比较模糊的。
三、前测后的教学实践
通过对前测中相关数据的整理、统计与分析,初步了解了学生对于从一个整体来认识分数的认知情况,也看到了其中存在的问题。因此,笔者认为这节课必须在以下两个维度上有所突破:一是通过剪,实现了“1”由一个物体到一组物体的自然过渡,把一些物体平均分成这样的一份或几份也可以用分数来表示,借助分数的含义理解部分与整体的关系;二是通过多重对比、分析,让学生体会到当“1”是一些物体时如何用分数表示部分与整体的关系,初步认识到一个物体与一个整体有相同的地方,就是平均分成几份分母就是几、几份分子就是几。
第一层次:一个物体的[SX(]1[]4[SX)]与多个物体的[SX(]1[]4[SX)]比较,感知部分与整体的关系。
课始,多媒体出示把一个正方形平均分成4份的图形(下左图),设问:涂色部分
能用哪个分数来表示,为什么这样不仅复习了一个图形平均分成4份,1份是它的[SX(]1[]4[SX)],
也让学生回忆分数产生的缘由,由此引入新课。随后课件复制左图,用剪的方法依次出示下中、右图(并消失中间图),设疑:现在这幅图的涂色部分还能用分数来表示吗
为什么学生出现了2种声音:
通过上述两个比较,学生在认知上已对一个图形的几分之一过渡到一个整体的几分之一有了突破,对部分量与整体量之间的关系有了初步感知,为下面的深入学习奠定了
基础。于是,笔者布置自主探索性作业,用两种不同的方法表示出[SX(]1[]3[SX)],以此来巩固一个
物体作为单位“1”和一些物体作为单位“1”的区别与联系。第二层次:相同个数用不同的分数表示及相同分数呈现不同个数的比较,深化部分与整体的关系。奥苏伯尔认为:学习就是要增加新旧知识之间的内在联系,以利于学生有意义地学习,使新知变得易于理解,并促进学习迁移,提高学习效率。通过第一层次的学习,学生对于把一个整体平均分成几份,每份占整体的几分之一,已经在大脑中建构起来。接着,课件依次出示下面三幅图。设问:涂色部分能用哪个分数来表示为什么
学生通过自己的操作实践与观察反思,充分结合分数的本质,理解具体情境中的数量关系,为今后进一步学习分数的意义、分数与除法的关系奠定基础,也为下一节课“分数简单应用例2”的学习做一定的铺垫。上述教学思考与实践中,笔者体会到,教学前测的设计应充分考虑文本所隐含的思想与文本所要体现的价值取向。而了解学生的认知起点正需要有“接地气”的教学前测,通过对前测的深入分析与思考,设计出贴近学生实际、符合数学的本体性知识的教学方案,让课堂教学更有厚度、有深度,更好地体现“生本教育”的理念。endprint
