经历学习过程 体现数学理解
2017-10-31张秋爽
张秋爽
【内容摘要】:概念的学习和儿童的数学理解一样,都是一个由浅入深、循序渐进的过程,数学理解的层次包括经验性理解、体验性理解、形式化(概念)理解和文化感悟理解。所以我们要给学生提供多样化的学习环境,设计有价值的数学活动,满足学生个性化的需求,让学生经历操作过程,经历思考过程,经历概括过程,经历应用过程,体现对数学的真正理解。
【关键词】:数学理解学习过程操作思考概括应用
近日,有幸听了赵东老师执教的《圆锥的认识》和吴正宪老师执教的《圆锥的体积》。这两节课是人教版数学六年级下册第一单元的内容。“圆锥”在生活中有着丰富的现实原型:儿童喜欢吃的冰激凌、小时候玩的沙子堆、经典的建筑金字塔等。学生能观察到形象的现实原型,从而激发探究的兴趣,逐步理解和掌握圆锥的特征和圆锥的体积计算方法。对于这样的概念教学,我们怎样才就能让学生获得对数学的理解呢下面让我们走进两位老师的课堂,寻找答案。
一、让学生经历操作过程,体现数学理解
让学生经历操作过程:给学生准备多样化素材,让他们参与其中,经过动手操作感悟形象化操作与抽象的概念之间的内在联系,从小事情、小发现中积累数学活动经验,建立自己的数学现实,形成相应的表象。这里的操作还包括从运动的角度展现知识的形成过程。
在几何图形的教学中,我们经常说: 點动成线,线动成面,面动成体。什么样的平面图形,旋转一周扫过的空间是圆锥呢老师让学生先想象再回答。
點动成线,线动成面,面动成体。什么样的平面图形,旋转一周扫过的空间是圆锥呢老师让学生先想象再回答。
生1:我觉得长方形沿着长或者宽旋转一周后形成圆柱;不可能形成圆锥,没有尖。正方形也是如此。
生2:梯形和平行四边形不论沿着哪条边旋转都不可能形成圆锥,所以我觉得是直角三角形。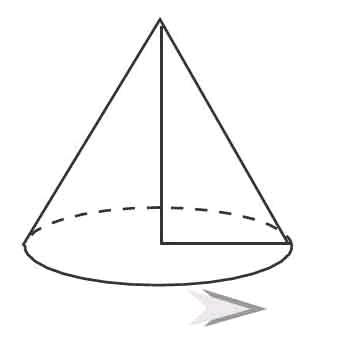
生3:我也觉得只有直角三角形旋转一周,形成圆锥的可能性最大。作为轴的直角边就是圆锥的高,旋转一周后,另外一条直角边就是底面圆的半径。
师:真的是这样吗请大家闭眼想象,一个直角三角形,以其一条直角边为轴旋转一周,扫过的空间形成一个圆锥体。请大家观察课件演示,印证一下自己的想象。
接下来引发学生进一步思考:旋转后形成的圆锥与原来的直角三角形有哪些联系用运动的观点认识图形,体现知识间的内在联系,在观察、想象、推理和表达中,发展学生的空间观念。
在学习《圆锥的认识》时,教师让学生课前亲手制作了圆锥体模型或把一个圆锥模型分解,学生对圆锥有了解,统一了认识:“圆锥有一个顶点,它的底面是一个圆;侧面是曲面,由一个扇形围成;圆锥底面周长与圆的周长、扇形的弧长必须相等;圆锥的顶点是扇形圆心角的顶点。”这样做充分利用了学生制作圆锥体的经验,让学生在充分体验的基础上获取对圆锥各部分名称的认识。除此之外,教师再次让学生制作一个圆锥体模型,材料是一个扇形和四个大小不等的圆形纸片,你觉得应该选扇形和哪个圆来组合呢
学生观察了图片,图1、图2的周长比扇形的弧长短,我们能想象:围出来的图形上边大,下边小;图4的周长比扇形的弧长长,围出来的图形上边小,下边大;只有图3的周长和扇形的弧长相等,围出来的图形正合适。
接下来讨论判断依据,小组合作利用学具进行验证。最后进行总结:判断扇形与圆能否正好组成圆锥,关键是看扇形的弧长是否与圆的周长相等。这种活动设计的价值在于: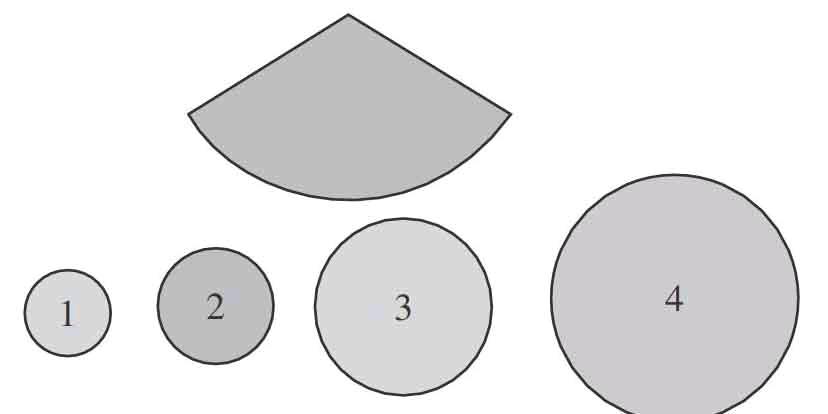
把圆锥体及其展开图进行比较,充分认识圆锥的特点,体现二维空间和三维空间的转化;并让学生经历“观察--想象--说理--动手验证--总结”的过程,进一步强化组成圆锥的扇形,它的弧长与圆的周长相等的关系。
二、让学生经历思考过程,体现数学理解
让学生经历思考的过程:经验+反思才能不断内化,形成自己对概念的认识;加强交流才能形成智慧的碰撞,不断丰富和完善自己的认知结构,在反思中积累思考的经验,不断总结方法性知识,感悟用数学思考问题的方式,体会数学的基本思想:抽象、推理和模型,更重要的是培养学生的空间观念。
了解了圆锥的组成,知道了各部分名称,圆锥的高也是一个重要概念。从圆锥的顶点到底面圆心的距离叫作圆锥的高。为了弄清楚扇形和高之间的关系:在相等的圆中剪出三个大小不同的扇形(如下图),用这三个扇形围成圆锥的侧面,三个圆锥的高一样吗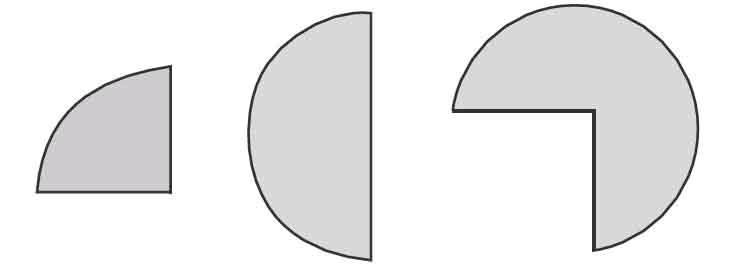
师:从图中你看出了什么要解决什么问题
生1:这三个扇形是从同样大小的圆中剪下来的,三个扇形的半径相等,我感觉三个圆锥的高也相等。
生2:我觉得三个圆锥的高不相等。
师:这是大家的猜想,小组合作,动手操作验证一下,说说你的发现。
(过了一会儿,学生有了答案。)
生3:我们小组通过操作,得出扇形的半径和圆锥的高没有一一对应的关系。
生4:扇形的半径并不是围成的圆锥的高。
生5:我们最初的想法是扇形的面积越大,围成的圆锥的高也就越大,实际与之相反。
师:你的意思是说:扇形的半径并不是圆锥的高;在半径相同的情况下,扇形的面积越大(弧长越长)高越短,面积越小(弧长越短)高越长。
这个活动中,学生的猜想是有“根据”的:半径相等,高就相等。但通过操作验证发现自己的猜测与事实不符,使学生产生认知冲突,学生会带着极大的兴趣探究其原因,最终深刻地认识到扇形的半径与圆锥的高不存在对应关系。此环节学生经历观察、猜测、推理、实验、验证、交流等数学活动,一方面强化了对高的认识,另一方面也极好地发展了学生的空间观念,积累了数学活动经验。endprint
三、让学生经历概括过程,体现数学理解
让学生经历概括的过程有多种途径。一是经历“情境引入—动手操作—抽象概念”的过程;二是遵从“多个例证—变式、反例—抽象概括”的步骤,三是按照“认知冲突—澄清、否定—抽象概括”的顺序,四是从“猜想—验证—抽象概括”的环节等。
学习《圆锥的体积》计算方法时,先让学生思考圆锥的体积与什么有关猜一猜体积公式是什么操作之后进行反思,与自己之前的猜想为什么不同圆锥的体积为什么和等底等高的圆柱有关在反思中积累思考的经验。
在学习圆锥的体积时,通常情况下,老师让学生往等底等高的圆柱里倒水、倒沙子,为什么不往其他的立体图形里倒呢是呀!书上是这样说的,教师就顺水推舟了,为什么呢在上这节课时,让学生先思考:以前我们学习平面图形的面积、立体图形的体积时都是怎样推导计算公式的
生1:学习平行四边形的面积时把它通过割补转化成长方形,根据等积变形找到它们之间的关系,得出平行四边形的面积。
生2:学习圆柱的体积时把它转化成近似的长方体,就推导出了圆柱的体积。
师:其实,以往平面图形的面积、立体图形的体积一般情况下是通过转化为已学图形的面积、体积来学习新知识的。那么对于圆锥的体积的学习,你认为和以前学习的哪个立体图形有关系
生3:我觉得圆锥的体积和圆柱的体积有关系,和长方体、正方体没关系。
生4:我也是这样认为的,因为它们的底面是相同的圆。
师:那你们猜一猜圆锥的体积应该怎样计算呢
生5:用底面积高。
生6:不可能是底面积乘高,肯定比这个乘积小。
师:那你感觉是多少呢
生6:我感觉可能是底面积乘高的一半。
生7:我也是这么认为的。因为圆柱是长方形或正方形沿着一条边旋转360°得到的;而圆锥是直角三角形其中一条直角边旋转360°得到的,直角三角形是长方形的一半,所以体积也应该是一半。
师:好!既然大家都同意,我们就试一试。圆锥和什么样的圆柱有关系体积之间又有什么关系
老师准备了一些圆柱,有等底不等高的,有等高不等底的,有等底等高的,还有既不等高也不等底的。学生开始尝试,在倒水过程中,有的圆柱和圆锥之间没有关系;有的正好能够倒3次,就能把圆柱倒满。于是从正好能够倒3次这个数据,思考什么样的圆柱和圆锥有这样的关系
每个小组亲自尝试后,得出结论,知道了为什么要往等底等高的圆柱里倒水,不往长方体的容器中倒水的原因,积累了数学活动经验和思考问题的经验。在这个过程中,有以下四个方面的特点:
⑴学生的操作是有需求的是猜想后想获得正确结果的好奇,此时学生的操作验证不再是盲目的:操作是基于动作表征,所有的操作是为了概念的形成,为了让学生逐步形成表象表征和语义表征做基础,使学生既知其然又知其所以然。
⑵学生理解了转化的方法:所有的平面图形的面积都是转化成已学过的图形来推导计算方法的,立体图形的体积也不例外。
⑶结论的形成有逻辑层次,不是直接对应的结论的达成,真正让学生经历知识的形成过程,把“原来的等底等高的圆柱和圆锥有关系这一最终的结果”分成三个层次:圆锥的体积和哪种立体图形的体积有关圆锥的体积和什么样的圆柱有关圆柱的体积和等底等高的圆锥有怎样的关系层层递进,最终聚焦到要解决的问题,这种层层缩小包围圈,筛选排除的方法是数学常用的方法。
⑷学生在知识迁移的过程中能不断纠正自己的认知偏差:圆柱是由长方形的长或宽旋转一周得到的,圆锥是由直角三角形的其中一条直角边旋转一周得到的,有一大部分学生猜圆锥应该是和它等底等高的圆柱体积的二分之一。通过操作,使学生纠正自己的认知偏差,体会操作对于结论正确与否的价值性。
这就是带着学生从头到尾地思考问题,从问题出发,问题引领需求,问题引领思维,进而解决问题。给学生提供多样的学习素材,让他们在不断尝试、筛选排除中获得正确的认知,积累思考经验,并不是一味追求简洁和正确的结果。让学生在过程中体验思考的快乐,形成解决问题的策略,达到对数学的理解,做到知其然又知其所以然。
四、让学生经历应用过程,体现数学理解
让学生经历应用的过程:学生对新概念掌握得如何,评价的标准不是学生能记忆相关的概念,而是在新情境中能够迁移,应用所学知识解决实际问题,积累应用的经验,感受数学的价值性。
学习了圆锥的特征之后,给学生提供生活中的圆锥。在自然界中有许多人为制造和自然形成的圆锥形物体。如沙子自然下落总会形成一个圆锥体的沙堆,其中还蕴含着深刻的道理呢!
教师准备一罐沙子,使它慢慢地从空隙中自然下落到桌面上,形成一个越来越高的圆锥形沙堆。像这样沙子颗粒自然下落,不久就会形成一个自然圆锥体,其中锥体的锥角为52度,这个角度就是自然塌落现象的极限角。
在生活中,我们常常会遇到一些自然形成的圆锥体,如粮堆、土丘等,它们的锥角都趋近于52度,因为在自然状态下锥角52度是最稳定的角,这是锥角52度普遍地存在于自然界的缘故。人们常常利用锥角52度的这一性质制造有52度角的各种物品。
金字塔几千年稳固地屹立在埃及大地上,从建筑力學上讲它有两个忠实“保镖”——52度“角”和方锥体的“形”。金字塔面与面之间的角度是51度50分9秒,这与有“自然塌落现象的极限角和稳定角”之称的52度角相差无几,而52度角被认为是最稳定的角,这说明金字塔是按照这种“极限角和稳定角”来建造的。
儿童的数学理解是一个由浅入深、循序渐进的过程。数学理解包括经验性理解、体验性理解、形式化(概念)理解和文化感悟理解。所以我们要给学生提供多样化的学习环境,设计有价值的数学活动,满足学生个性化的需求,只有经历过程,习得方法,渗透思想,才能加深儿童对数学的理解,从而让更多的儿童觉得数学有趣、好玩、有用、有价值。endprint
