PEG／PLGA纳米纤维膜的制备及其参数优化*

赵月，陈灶妹，何婷，陈柯君，江丽，张俊辉，万华印，李茹冰△

（1.广东药科大学，广东 广州510006；2.广州军区广州总医院，广东 广州510010；3.广州市电纺生物科技有限公司，广东 广州510604）

1 引 言

静电纺丝是一种利用电场力驱动成纤最简单、高效的方法，其制备的纳米纤维膜具有表面积大，孔隙率高及易于实现表面功能化等特点，结构类似于细胞外基质，能够增强细胞迁移和增殖［1－2］。目前，静电纺丝纳米纤维膜已在生物医学领域得到广泛应用，如组织工程技术支架、创伤敷料和药物载体等［3］。

聚乳酸－羟基乙酸共聚物（PLGA）是一种无毒，可完全生物降解的聚合物，具有优良的成形性和生物相容性，降解产物易排除体外，被认为是最具发展潜力的医药高分子材料［4］。但由于其力学性能强度不够、亲水性差等缺点，在生产和使用过程中容易断裂、滑动，同时静电纺丝制备的纳米纤维呈无纺布形式排列，它不像传统方法得到的纤维那样具有高度的取向性，这在很大程度上限制了PLGA的应用［5］。为了改善PLGA纤维膜的亲水性，力学性能，优化其防粘连效果，最简单有效的方法是掺加一定量的如聚乙烯吡咯烷酮（PVP）、聚乙二醇（PEG）等含有柔性链段，亲水性较好的聚合物［6］。

响应面法（response suface methodology，RSM）是一种数字和统计结合的方法，用来对所研究的响应受多个参数影响的问题，通过建模和分析寻求最佳组合条件进而优化该响应值。响应面优化最常用的设计方法主要有以下两种：（central composite design，CCD、box behnken design，BBD）［7］。但较 CCD而言，BBD具有试验次数较少，预测精准度高和实验因素不会同时处于极端水平等优势［8］。由于目前静电纺丝技术制备纳米纤维的力学性能与其影响参数之间的关系无法准确地数字化，而采用响应曲面法则可以通过建模和分析，不仅可以建立拉伸强度和实验参数的二元回归模型，通过对所得模型的分析，可得到各个因素对拉伸强度的影响程度，而且可以通过响应面分析的三维图更直观地看出拉伸强度随着实验条件的变化趋势［9－10］。本研究采用三因素（PEG含量、纺丝速度和电压）三水平的BBD方法，系统地研究了工艺参数对复合纤维膜力学性能影响，并进行优化，以获得最佳的参数条件。

2 材料与方法

2.1 材料与仪器

聚乙二醇，粘均分子量，Mv＝6000，Beijing Solarbib Science＆technology Co.，Ltd；聚乳酸 －羟基乙酸共聚物，粘均分子量，Mv＝90000，济南代罡生物材料有限公司；三氯甲烷（CHCl3），分析纯，天津市宏达化学试剂厂；N，N－二甲基乙酰胺（DMAC），分析纯，麦克林（MACKLIN）；丙酮（AC），分析纯，广州化学试剂厂。

电子扫描显微镜，JSM－7001F型，上海百贺仪器科技有限公司；胶粘带初粘性测试仪，BLD－1007型，东莞博莱德仪器有限公司；高压静电纺丝机，TL－Pro型，深圳市通力微纳米科技有限公司；磁力搅拌水浴锅，XMTD203型，金坛市良友仪器有限公司；接触角测试仪，PT－705－B，东莞市诚鼎仪器科技有限公司。

2.2 实验方法

2.2.1 PEG／PLGA复合纤维膜的纺制 将PLGA和 PEG按比例混合溶解在 V（AC）：V（DMAC）：V（CHCl3）＝5：3.5：1.5混合溶剂中，在磁力搅拌下37℃溶解搅拌，静置脱泡，然后装入注射器中，设定压强，接受距离为19 cm，纺丝速度等参数，控制温度为35℃，进行五喷头（21G）静电纺丝；将制备出的纳米纤维膜在真空干燥箱中干燥备用。

2.2.2 响应面实验法优化静电纺丝条件 （1）单因素实验选取PEG含量、电压、纺丝速度等因素，分别进行单因素实验，分析其对PLGA／PEG复合纤维膜力学性能的影响。（2）在单因素实验的基础上，以拉伸强度为响应值，利用Box－Behnken设计三水平试验，因素编码和水平见表1。

表1 Box－behnken实验设计的因素和水平Table 1 Factors and levels of Box－behnken design

2.2.3 纳米纤维膜的力学性能测试 采用BLD－1007型胶粘带初粘性测试仪测试纤维膜厚度，每一样品取3个点。用刀片从纤维膜上取尺寸为 10 mm×40 mm的细长条样品，然后在常温下对样品进行测试，试样夹持长度30 mm，拉伸速度10 mm／min，每一样品测5个数据，取平均值。

2.2.4 接触角测定 分别剪取长宽为1 cm×3 cm大小的 纳米纤维膜，采用接触角／界面张力测量仪测定，首先在样品上滴加直径约为1 mm左右的去离子水滴，然后在接触角／界面张力测量仪的显示器上读出接触角的数据。每个样品上滴加五滴去离子水，平行测五次，求平均值。

3 结果与讨论

3.1 单因素实验结果

3.1.1 PEG含量对复合纤维膜的拉伸强度的影响见图1，PEG／PLGA复合纤维膜的拉伸强度大于纯PLGA纤维膜的拉伸强度；当PEG含量在0%（质量分数）～7.5%（质量分数）之间，随着PEG含量的增加，复合纤维膜的拉伸强度增加，这可能因为含有柔性链段PEG的加入，使复合膜的宏观柔性增加，从而表现为断裂强度增加。但PEG含量进一步增加时，复合纤维膜干燥后开始变透明，拉伸强度也降低，可能是因为加入大量PEG时，由于熔点较低，在干燥时发生熔融。故选取PEG含量为2.5%（质量分数）、5%（质量分数）、7.5%（质量分数）作进一步分析。

图1 PEG含量对纤维膜拉伸强度的影响Fig 1 The effect of factors PEG concentration on tensile strength of fiber film

3.1.2 纺丝速度对复合纤维膜的拉伸强度的影响见图2，纺丝距离一定时，随着纺丝速度的增加，拉伸强度呈现先增后降的趋势。溶液的流速决定纺丝过程中喷头处的溶液数量和喷射速度。静电纺丝得到的纤维主要呈无纺布形式排列，它不像传统方法制备的纤维那样具有高度的取向性，纺丝速度增大，纤维直径随之增大，纤维间纵横交错程度变小，所以拉伸强度变小，反之亦然。当纺丝速度小于1 ml／h时，针尖出现断流。因此，综合考虑，选取纺丝速度 1、3、5 ml／h作进一步分析。

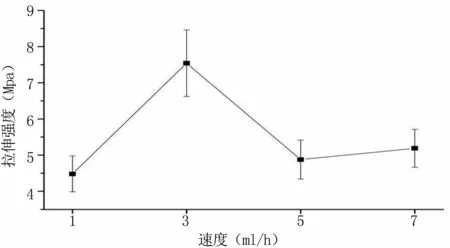
图2 纺丝速度对纤维膜拉伸强度的影响Fig 2 The effect of factors spinning speedon on tensile strength of fiber film

3.1.3 电压对复合纤维膜的拉伸强度的影响 见图3，电压由13 KV升高至19KV，复合纤维膜的拉伸强度也明显增加。由于当电压升高时，电场强度也增大，对喷射流的拉伸作用增强，分子取向增大，从而导致纤维膜的力学性能升高，宏观表现的拉伸强度也随之增大。但当电压进一步增大时，纺丝液从喷头直接喷出导致射流不稳定，并且电压过高，针尖偶有火花，故而不能进行探索。因此，综合考虑，选取电压为17、19、21KV作进一步分析。

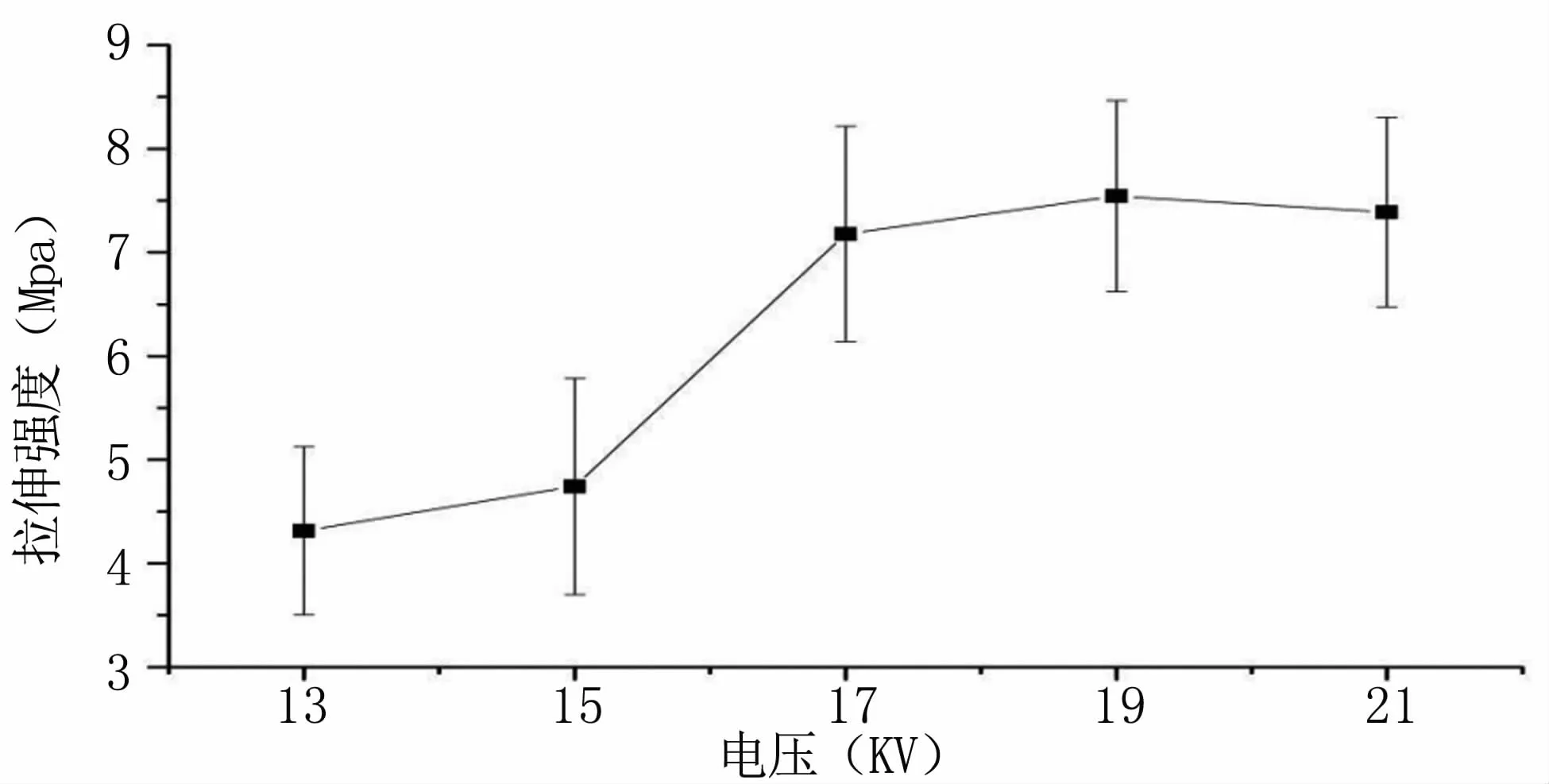
图3 电压对纤维膜拉伸强度的影响Fig 3 The effect of factors electric field intensity on tensile strength of fiber film

3.2 多项式响应面建立及分析

3.2.1 表2示出Box－behnken设计的17组实验和对应的响应值，利用Design－Expert7.1.3软件对数据进行回归分析，得到PEG／PLGA复合纤维膜拉伸强度的二次多元回归方程为：D＝－92.86488＋1.05240*A＋0.27413*B＋9.92925*C－0.078500*A*B－0.021000*A*C＋0.038125*B*C＋0.063760*A2－0.099750*B2－0.25913*C2

表2 Box－behnken实验设计表和响应值Table 2 Box－behnken arrangement forl factors and response

对上述回归模型进行方差分析和回归系数的显著性检验，结果见表3。从表3可知，该模型的P＜0.0001，表示该模型对响应值影响是显著的，该模型是有效的，因素 A，C2对纤维直径影响显著，因为其P＜0.05，而其他因素对拉伸强度影响不显著。该模型中决定系数R2为0.9602，说明该模型对纤维直径的预测效果达到96.02%，表明预测模型与实验拟合很好。失拟项P＝0.3017＞0.05，说明模型失拟不显著，与实际拟合较好。校正系数等于0.9090，预测系数等于0.8800，两者相接近，对模型的预测会产生正面效应，表明回归模型能描述响应值的变化，因此，可利用该模型对复合纤维膜的力学性能进行分析和预测。

3.2.2 模型交互项的解析 图4（a）－（c）是根据二次多项式回归方程作出的响应面图和等高线。图4（b）、（c）等高线呈椭圆趋势，证明 PEG含量和电压，纺丝速度和电压的相互作用对拉伸强度的影响较大。在一定范围内，3个因素的增加均会造成拉伸强度的增加。从图4可以明显看出在PEG含量为5%，纺丝速度为3 ml，电压为19 KV时，拉伸强度出现最大值。

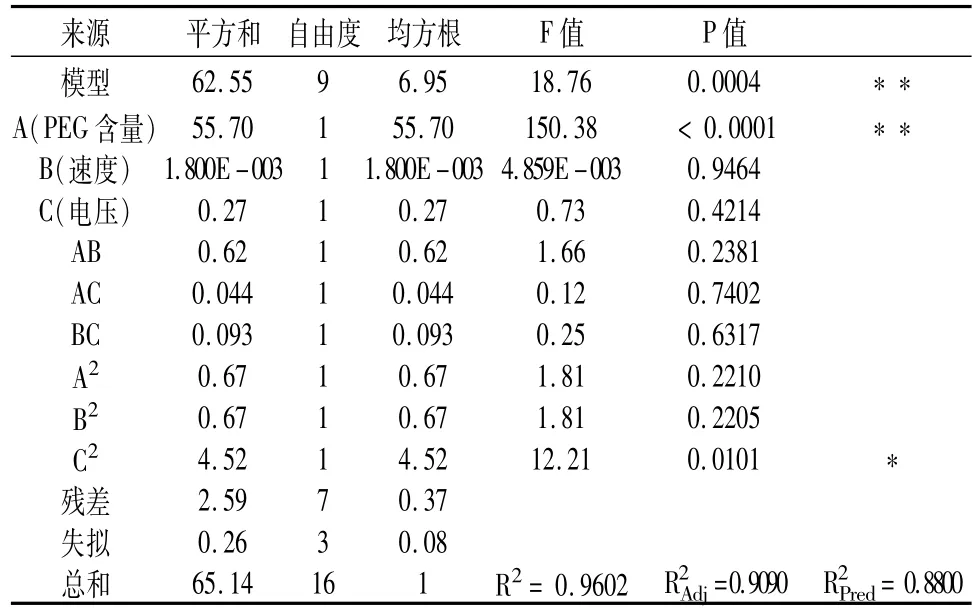
表3 回归方程系数的显著性检验Table3 Significance test of coefficient in regression equation

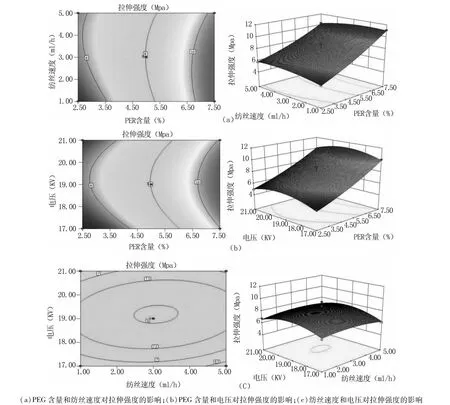
图4 响应面等高线图显示各因素对拉伸强度的影响（a）Effect of PEG concentration and flow race on tensile strength；（b）Effect of PEG concentration and electric field intensity on tensile strength；（c）Effect of flow race on and electric field intensity on tensile strengthFig 4 The effect of various factors on the tensile strength of the response surface and Contour Plots

3.3 模型适合性检验

模型适合性检验与构建模型同等重要。模型诊断主要是残差诊断，残差诊断主要包括标准化残差和学生化残差［7，9］。

3.3.1 残差的正态概率图 正态概率图主要用于验证残差正态性，如果残差符合正态性，那么此图将近似为一条直线。但正态概率图常出现的一个瑕疵是某些残差远远大于其它的残差，此类残差称为离群值。过多的离群值将严重歪曲方差分析［11］。从图5可以看出，残差各点的分布大部分在直线周围，证明该模型拟合较好。

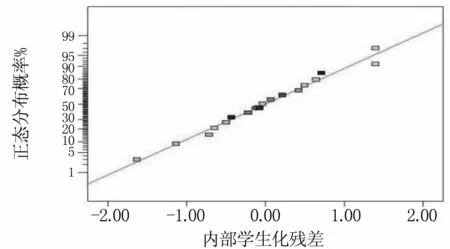
图5 残差的正态概率图Fig 5 Normal probability plots of residuals

3.3.2 依时间顺序的内部学生化残差图 除了正态性及残差的方差齐次性的验证，还需验证残差之间的独立性。依时间顺序的残差图是探测残差关联性的有效工具。随着实验的进行，如果残差图呈现单一正或负的趋势，则表明残差间存在关联性［12］。从图6可以看出，残差值没有出现或正或负一边倒的分布，而是既有正值又有负值，证明该模型拟合较好，且具有相对独立性。

图6 依时间顺序的内部学生化残差图Fig 6 In the time sequence of the internal student of the residual figure

3.4 纤维膜的亲水性

一般当材料分子与水分子之间的相互作用的内聚力大于水分子之间的内聚力时，水分子能很快在材料表面铺散开来。此时，在材料、水和空气水分子能很快的交点处，沿水滴表面的切线与材料表面所成的夹角（称润湿角）θ≤90°，材料呈现亲水性。若θ＞90°，材料呈现疏水性［13－14］。从图 7（a）可以看出，纯PLGA纤维膜上的水珠基本保持原球形，浸润不明显；从图7（b）可以看出，加入PEG后的纤维膜上的水珠无法保持原球形，浸润明显。说明加入适量PEG可以改善纯PLGA膜的亲水性，另外，PEG／PLGA纤维膜亲水性随PEG含量增加而提高。

图7 静电纺丝膜接触角：（a）纯 PLGA纤维膜，118°；（b）5%PEG／PLGA纤维膜，86°。Fig 7 Nanofiber membrane contact angle：（a）pure PLGA fiber membrane，118°；（b）5%PEG／PLGA fiber membrane，86°。

4 结论

通过静电纺丝方法制备得到PEG／PLGA复合纳米纤维，通过响应面试验分析纺丝工艺条件对拉伸强度的影响情况，并对工艺参数进行了优化。通过回归分析建立了PEG质量分数、电压和纺丝速度对PEG／PLGA复合纳米纤维直径的多元响应面模型，其预测值与实际值能较好的拟合，说明在PEG／PLGA复合纳米纤维直径的预测上是有效的。其中，PEG含量是影响纤维直径的最显著因素，其次是电压和纺丝速度。最优纺丝条件为，PEG含量5%、电压10 KV、纺丝速度3 m l／h。在此条件下得到纳米纤维膜亲水性得到有效改善。