基于PCA多导联的癫痫脑电信号分类及致痫灶定位研究*

李冬梅，尔西丁·买买提，杨日东，陈子怡，田翔华，董楠，张洋，周毅，△

（1.新疆医科大学研究生学院，新疆乌鲁木齐830011；2.新疆医科大学第一附属医院神经内科，新疆乌鲁木齐830011；3.中山大学中山医学院生物医学工程系，广东广州510080；4.中山大学附属第一医院神经内科，广东 广州510080）

1 引 言

癫痫是由脑部神经细胞群高度同步化异常放电引起的慢性神经系统综合症［1］。其发作可能会引起患者认知障碍、惊厥、受伤甚至死亡［2］，是老年痴呆、中风之后的第三大神经系统疾病［3］。据调查，全球约有0.7%的人口患有癫痫［4］。尽管很多患者可以通过临床药物治疗对疾病进行有效控制，但仍有大约30%的患者是对药物无直接反应的［5］，对于药物无法控制其发作的癫痫患者，目前可使其痊愈的唯一手段是手术切除致痫灶，而手术成功的关键在于对致痫灶的精准定位。

脑电图（electroencephalogram，EEG）长期记录了大脑的电生理活动［6］，具有明显的非平稳性和非线性特征［7］，在神经系统疾病的诊断中具有非常重要的作用。目前临床上对致痫灶的定位多采用脑电信号与影像学相结合的方法，EEG信号具有较高的时间分辨率，影像学（functionalmagnetic resonance imaging，fMRI）则具有较高的空间分辨率，二者相结合就能准确的定位出致痫灶的位置［8－9］。然而，临床脑电信号主要是基于人工判断、诊疗水平由医生理论知识和经验的限制［10］，通过大面积开颅采集脑电信号不仅会对患者造成很大的伤害，也会对资源造成浪费。致痫灶一般只有几平方厘米，大面积开颅无疑也采集了大量无利用价值的脑电数据，能否在尽量降低对患者损伤的基础上采集到有价值的脑电数据是目前亟待解决的问题。因此，本研究提出一种基于PCA的方法分析患者头皮脑电数据来进行初定位的方法，达到初步确定致痫灶大致位置的目的，临床可以在此基础上通过小面积开颅来采集高质量脑电数据进行精准定位，这样既减少了对患者造成的损伤，也节省了临床医疗资源。

本研究提出了基于多特征指标的癫痫致痫灶定位方法。首先，选取 Hurst指数、Lyapunov指数、样本熵、排列熵、小波熵五个特征向量来表示脑电信号的非线性特征，并对特征向量进行PCA降维处理，将处理后的特征值输入已构建好的分类器中，对脑电信号进行准确分类；其次，将已分类好的正常脑电信号结合医学统计的置信区间，构建医学参考值范围；最后，将癫痫脑电信号输入医学参考值范围，观察各导联的数值变化程度，并将结果进行可视化处理。

2 特征提取

EEG信号是一种非线性时间序列。为了能更好地提取出脑电信号的特征，本研究选择常见的非线性动力学指标（Hurst指数、Lyapunov指数、排列熵、样本熵、小波熵）对脑电信号进行处理分析，现将指标介绍如下：

（1）Hurst指数：由英国水文学家 Hurst提出的基于时间序列分析的指标，其可作为在混沌和分形学科中判断时间序列混沌性的统计参数，它能很好的揭示出时间序列中的趋势性，常被用于定量刻画时间序列的长程相关性［11］。

（2）Lyapunov指数：可定量描述相邻点相互分离的快慢或混沌吸引子中轨道分离的快慢，它表征了相空间中邻近轨道间收敛或发散的平均指数增长率。在对信号的非线性混沌度进行定量分析时，通过Lyapunov指数可以表征大脑活动不同状态下的特征。研究表明，Lyapunov指数对于部分性发作癫痫病人EEG信号的动力学特征具有很好的描述能力［12］。

（3）排列熵（permutation Entropy，PE）：一种新的衡量时间序列复杂度的非线性动力学特征指标。计算时间序列复杂度方面该指标与Lyapunov指数相似，但与Lyapunov指数相比，排列熵具有计算简洁、数据量小、抗噪能力强等特点，在非线性动力学应用方面有良好的特性［13－14］。

（4）样本熵（sample entropy，SampEn）：由 Richman和Moornan提出的一种新的时间序列复杂性测度方法。可用于测量两个新信息发生的条件率。样本熵是一种与近似熵类似，但精度更好，可降低近似熵的误差。

（5）小波熵（wavelet entropy，WE）：由于人的大脑在不同状态时EEG也会在不同频段上产生能量的变化，小波熵就可以反映出这些变化。时间序列由小波分解信号后计算得出的熵值。小波熵是对随机信号无序程度的一种测量［15］，可用于估计EEG的复杂程度。

3 主成分分析与随机森林

3.1 主成分分析

主成分分析（principal component analysis，PCA）是一种将多指标问题转化为较少的综合指标的重要统计方法［16］，它使我们能够使用少量的综合指标（这是相互不相关的）提供最原始的指标信息，而且还可以更方便快捷地解决问题。脑电信号具有非平稳性的特点［7］，导联之间关联性大，且极易受噪声干扰。PCA作为多维数据分析常用的方法，既能除去脑电信号不同类别之间的相关性，也可同时处理多导联的脑电信号，从而简化脑电信号的分析处理。因此，利用主成分分析对脑电信号进行特征提取具有独特的效果。

假设m个变量X1，X2，…，Xm的n次提取数据矩阵为X＝（Xpq）n×m。由于处理分析得到的数据的单位和数量级之间的差异，数据处理应规范化。其主要步骤如下：

（1）计算各个指标的样本均值与标准差

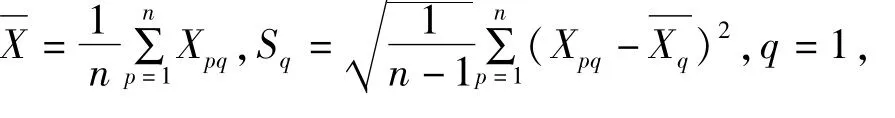
（2）对Xpq进行标准化处理，计算其标准化矩阵

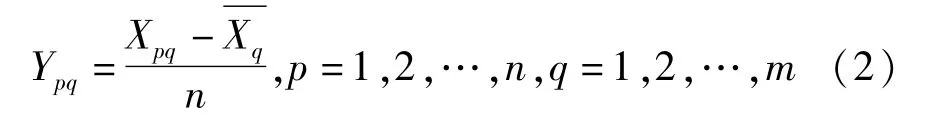
（3）依据所得的标准化矩阵Y＝（Ypq）n×m，计算其相关系数矩阵R

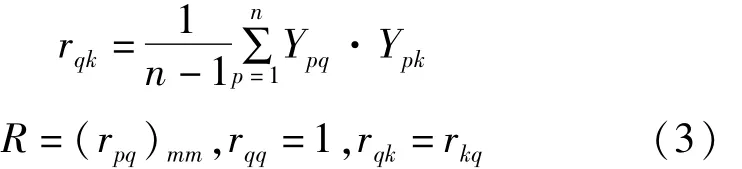
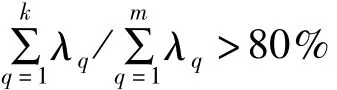
（5）建立主成分方程，可得前K个主成分的样本值

3.2 随机森林（Random Forest）

随着人工智能的发展，机器学习被越来越多地应用于经济学、生态学等领域［16－17］。随机森林最早在2001年由 Leo Breiman和 Adele Culter提出［18］，随机森林由许多的决策树构成，由于决策树是由随机方法构成的，也称为随机决策树，具有很高的预测精度与学习能力。其基本思想是：对训练数据进行随机采样，随机构建一片森林，在这片森林中每棵树就是一个决策树（每棵决策树是相互独立的）；当测试样本进入随机森林时，森林中的每个树分别判断，并进行投票。随机森林的决策结果是所有决策树分类结果的集成，通常随机森林会选择投票数最多的分类结果作为最终结果。

随机森林算法中的样本与决策树均为随机选取。将每棵决策树的“投票”分类结果进行集成，可以确保结果的稳定性与客观性；并且随机森林不需要人为参与地设置每个节点阈值，完全由算法自动实现对每棵决策树的生长与修剪过程，最大限度地避免了人为因素对最终结果的干扰。

4 实验结果与分析

4.1 临床数据采集

实验数据来自于新疆医科大学第一附属医院神经科脑电图室，采样频率均为200 Hz，对12例颞叶癫痫患者脑电数据进行研究。实验采用数据均为19导头皮脑电数据，采集后由临床脑电图仪进行预处理后存储于医院数据库中，因此可直接将其进行研究。

4.2 实验过程

首先，构建分类器，随机选取1病例的脑电数据进行特征值提取，将得到的多个特征值进行PCA降维处理后，随机选取训练集数据输入到分类器构建的分类器算法。

构建好分类器后，将剩余的11例数据作为测试集数据输入到构建好的分类器中，进行分类，得到分类结果。

综合降维后的特征向量，计算其在不同时期特征向量，得到描述头皮各电极脑电数据的复杂度和各电极动力学变化程度，从而找出动力学变化最明显的区域，以此实现对致痫灶的初定位。

4.3 实验结果分析

4.3.1 分类效果 对特征值进行PCA分析，提出主要成分的向量，并将向量进行综合计算。将综合的特征值也进行分类，并与单一特征值的分类效果进行比较。图中x轴表示不同特征值，y轴表示分类器的分类准确率，从图1中可以看出，综合的特征值的分类效果均比单一特征值的分类效果好，综合的分类准确率在90%以上；熵类的特征值（SampEn，Mpe，Wavelet）分类效果较非熵类（Lyapunov，Hurst）而言，准确率略高。

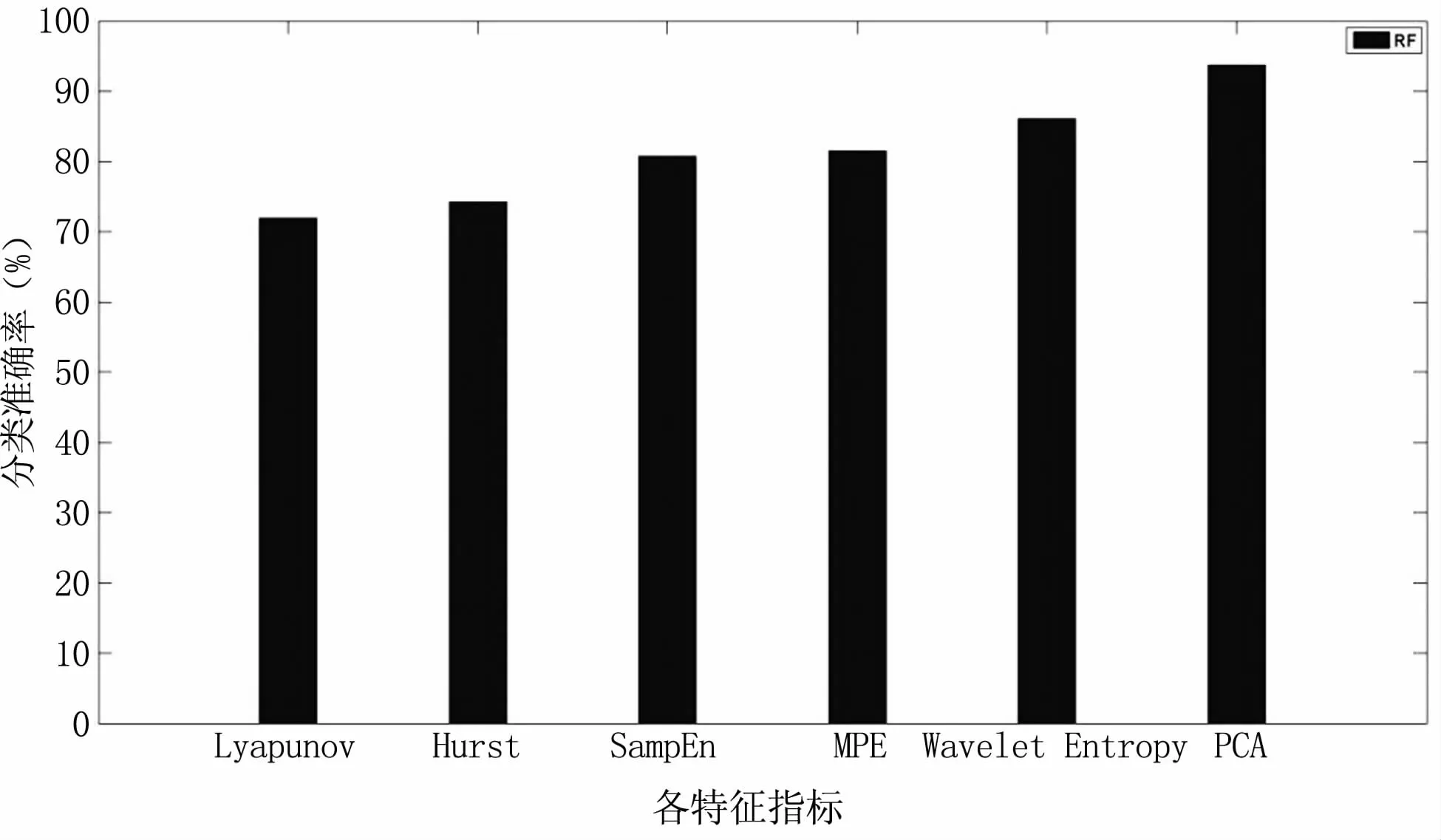
图1 PCA降维后综合特征值与单一特征值的分类结果Fig 1 The results of the classification of the PCA dimension reduction and the single feature value

为了进一步验证综合特征向量与单一特征向量分类准确率的优劣，本研究采用受试者工作特征曲线（receiver operating characteristic curve，ROC曲线）作为诊断试验性能的评价，其经过转变诊断阈值，得到多对真（假）阳性率值。以假阳性率（1－特异性）作为横坐标，真阳性率（敏感度）作为纵坐标，绘制ROC曲线，曲线下面积（area under curve，AUC）反映诊断试验的综合精度。本研究将各特征值的分类结果导入 SPSS，绘制 ROC曲线并计算 AUC值，其AUC值分别为 0.719，0.742，0.807，0.815，0.86，0.937，均显著大于随机分布模型的AUC值（0.5），见图2，其中PCA综合特征值分类结果的AUC值最大，说明它可以更加准确地对脑电信号进行分类。经统计检验，除PCA综合特征值与其他单一特征值之间差异显著，其他单一特征值均两两之间差异不显著（P＞0.05）；且熵类特征向量对应的AUC值均大于非熵类的AUC值。

图2 PCA降维后综合特征值与单一特征值分类结果的ROC曲线图Fig 2 ROC curve chart of the resultsof PCA dimension reduction and single feature value classification

4.3.2 致痫灶初步定位 若正常脑电数据计算的特征值服从正态分布，利用医学统计的置信区间，则可以用这些特征值构建一个医学参考值范围，一旦某段数据的特征值偏离了医学参考值范围，就有理由相信该段数据不是正常的脑电数据。将某导联在发作过程中的特征值放入对应导联的医学参考值范围，偏离的数据段越多、偏离得越远，则认为该导联的动力学变化越明显，以此来定量衡量各导联动力学变化的程度。

因此，先对正常脑电数据计算的特征值验证其正态性。选取100段正常脑电数据的特征值，对其进行正态性检验，观察是否具有正态性。结果见表1。

表1 正态性检验结果Table 1 Test results of normality

由于所选样本为小样本数据（小于2000），因此选取S－W检验，并且当P＞0.1时认为样本服从正态分布，所以本研究认为正常脑电数据的特征值服从正态分布。随后取其均值μ和标准差s，构建95%的置信区间；将患者发作过程中的脑电数据计算得来的特征值放入到已构建好的置信区间之内，筛选出每个导联上位于正常范围以外的数据段，并计算所有数据段偏离置信区间的距离之和，将结果进行可视化处理，观察各导联的颜色深浅程度。见图3，图中右侧彩色条的颜色随着数值的增大颜色逐渐加深，左侧的图中显示出各导联的位置及数值对应颜色的变化。图中可以看出，T5导联颜色深度明显。

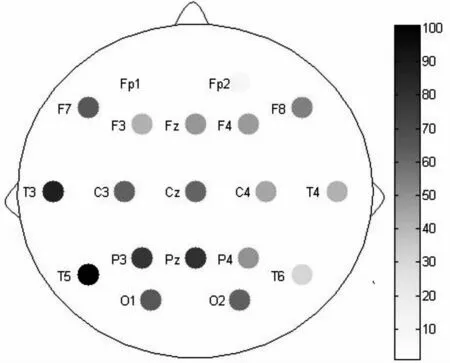
图3 各导联特征值的变化Fig 3 Changes in the characteristics of the lead

以颜色最深的导联为圆心，取偏离程度最大的两个导联中间位置为半径进行画圆，将该区域和致痫灶一同置于大脑地形图中，见图4，深黑色代表动力学变化最明显的电极，绿色圆区域为由深黑色电极确定的初定位区域，红色圆点代表致痫灶所在位置。由图可见，对颞叶癫痫患者初定位的区域都包含了临床确诊的病灶区域，则对该患者的初步定位成功。

图4 致痫灶初步定位Fig 4 Initial location of epileptic foci

依据此方法，对12位癫痫病例进行了初步致痫灶定位（见图5）。由图4可以看出，临床诊断出的致痫灶确切位置与我们计算出的动力学变化最明显的电极最接近，这也说明了利用PCA这一抗噪性强的非线性综合特征指标来对头皮脑电信号进行分析是可行的。

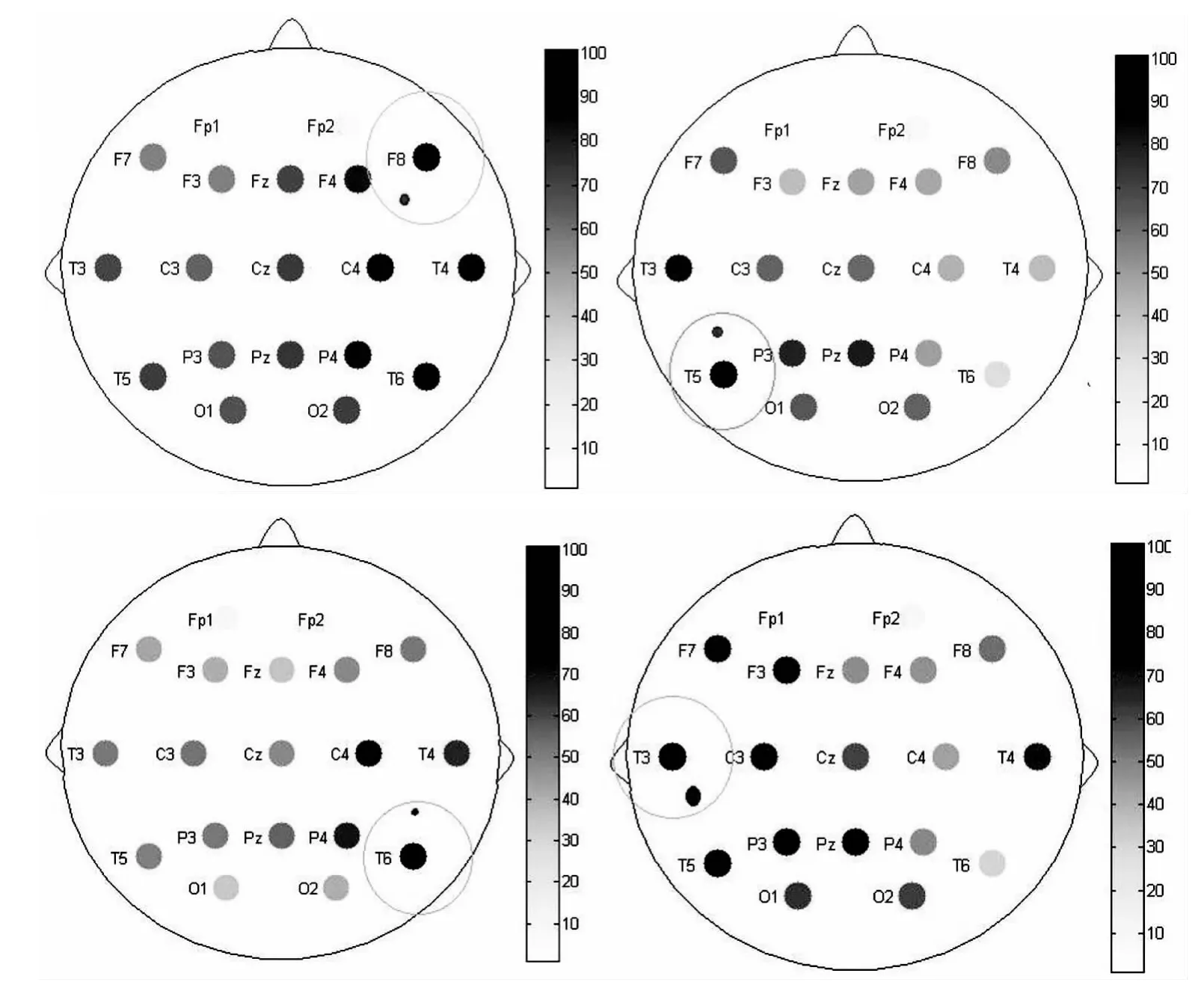
图5 12位癫痫病例初步致痫灶定位Fig 512 epilepsy cases of epileptic foci

5 讨论

在本研究中，主成分分析被用来提取EEG信号的非线性特征指标，并将随机森林运用于癫痫脑电信号的分类中。在对脑电信号进行分类的过程中，采用了一种新的综合性特征指标，这种指标从多个角度对脑电信号进行了分析及综合，并与医学统计学相结合，对部分性癫痫患者的致痫灶进行了初步的定位，成功对12位癫痫患者进行了初定位。此方法能快速、敏感地提取出脑电信号中重要的信息，具有较好的抗噪和抗干扰能力，为临床上建立局灶性癫痫病灶部位的搜索模型提供了理论基础。

目前，对于可以采用手术切除致痫灶来进行治疗的患者，如何在尽量降低患者损伤的基础上准确的定位出致痫灶所在位置成为手术治疗的关键。本研究将非线性动力学与医学统计学相结合，多方位地对癫痫脑电信号进行分析研究，很有可能为临床上定位致痫灶开辟一条新的路径，通过对癫痫患者无损的头皮脑电信号进行初定位，在此基础上通过临床小面积开颅，采集高质量脑电数据进行精准定位，不仅减少了对患者造成的损伤，也节省了临床医疗资源。