三角模糊可拓理论在老旧电梯运行失效可能性评价中的应用

马幸福

（湖南电气职业技术学院 电梯工程学院 湘潭 411101）

检验评价

三角模糊可拓理论在老旧电梯运行失效可能性评价中的应用

马幸福

（湖南电气职业技术学院 电梯工程学院 湘潭 411101）

为了准确判断老旧电梯运行失效的可能性，应用三角模糊理论结合层次分析法进行风险评价，拓展评价维度，克服传统评价偏差。首先从故障频率、日常运行管理、使用年限3方面构建评价模型；然后由专家通过三角模糊数建立两两比较三角模糊判断矩阵；最后，利用线性规划方法计算模糊权重，得出评价指标最终权重。结果表明，安全部件失效的风险最大，应予以重点考虑，验证了该方法的可行性。

三角模糊数 老旧电梯 层次分析法 风险评价

电梯的设计使用寿命一般为10～15年左右，由于受维修保养和使用工况等多种因素的影响，电梯整机使用寿命存在很大差异，只要能通过特种设备检验检测部门的检测，电梯就能一直使用，因此，有的老旧电梯运行已经超过了15年。由于超期运行，电梯部件严重老化，控制技术落后，老旧电梯的可靠性和安全性潜在风险加大，由运行失效引发的安全事故逐年增多。因此，如何对老旧电梯运行失效可能性进行有效评价成为电梯安全亟待解决的重大问题。

电梯的风险评价起源于欧洲，目前并未形成统一的评价标准与评价方法，常用的是层次分析法，国内学者也进行了大量研究，提出了很多新的评价方法。如蔚光庆等[1]提出了模糊定量安全评估方法，门智峰等[2]提出了定量加权平均分析法，范俊燕等[3]提出了基于机器学习的电梯安全评价方法，徐泽水[4]提出了模糊有序加权平均算子方法。老旧电梯运行失效受机械系统、电气系统、维修保养、外界使用情况等众多因素影响，应用传统评价方法具有一定的局限性。本文利用模糊理论，在层次分析法中结合三角模糊数量化风险指标，由一维评价值拓展成三维评价值，建立安全风险评估模型，计算评估指标最优化权重值，对影响老旧电梯运行失效的风险因素进行综合评价，克服传统评价方法的经验性与人为主观性。

1 基本定义

层次分析法在对两两评价指标重要性进行打分比较时，由于专家打分的模棱两可性容易导致判断矩阵出现病态，不易通过一致性检查，从而需要重新进行打分。模糊可拓理论以模糊集合与模糊逻辑为基础，适用于解决有人员参与的相关界限不分明甚至很模糊的问题。

定义[5]模糊数A的隶属函数为

为了描述评估准则i相对评估准则j的重要程序，定义三角模糊数ij表示评估准则的比较结果，具体标度取值关系见表1。

表1 三角模糊数标度取值关系

传统层次分析法利用1～9标度进行取值打分，在构造判断矩阵时容易出现不一致性，导致逆序问题出现。而采用三角糊糊数形式构造判断矩阵，直接从不一致性或不完全的判断结果中求解优先级向量，意味着只需要求解模糊数ij即可解决优先级排序问题。

2 风险评估过程

2.1 评估流程

实现老旧电梯整机系统安全风险评估的具体流程如下：

1）通过设计评估表格，以问卷调查表等形式聘请电梯专家对老旧电梯的环节可能性风险、环节严重性风险、部件可能性风险、部件严重性风险、日常运行维护及日常档案管理等之间的相互重要性进行打分，建立风险评估指标体系。

2）建立老旧电梯整机系统风险评估模型，应用三角模糊理论及线性规划理论计算各风险指标的模糊值。

3）确定各评估指标的权重值和评估准则层的最终优先级排序结果，判断老旧电梯整机系统结构的安全健康程度。

2.2 评估模型的建立

在实际过程中，老旧电梯的运行安全性受外部使用环境安全、本身机械部件及电气部件功能安全、维护保养人员及使用管理人员操作等多方面因素影响。本文仅从运行故障频率、日常运行管理及使用年限3方面的准则来对风险因素进行排序，建立风险评估模型如图1所示。

图1 老旧电梯整机系统风险评估模型

2.3 模糊优先级的排序

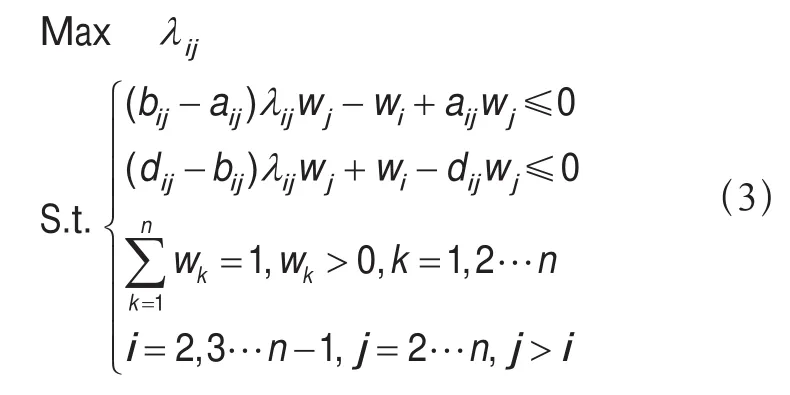
其中λij表示线性隶属，衡量的是wi/wj满足中间值bij的程度。存在一个最优解向量(wi/ wj,λij)，使式（3）具有最大隶属度，通过求解线性规划方程，避免了判断矩阵一致性检验问题。

利用文献[4]中的基于FOWA算子的三角模糊数互补判断矩阵法计算最优解向量的权重值。利用该方法可以得到不同的专家对准则层及元素层指标的模糊权重；为将不同专家的意见融合在一起，并体现各自主观判断的差异性，运用模糊度排序方法对模糊权重重新排序，计算指标排序公式为：

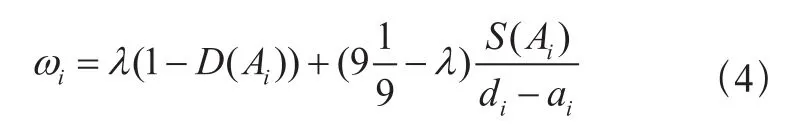
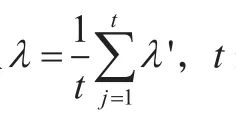
3 应用实例分析

为了验证该方法的有效性，选取老旧电梯运行可靠性的整机系统作为评估对象，从故障频率、日常运行管理、使用年限3个方面建立图1所示老旧电梯整机系统风险评价模型。通过3位电梯专家对运行故障频率、日常运行管理、使用年限3个准则层指标进行打分，建立两两比较三角模糊判断矩阵，见表2～表4，利用matlab工具箱编制线性规划函数程序，分别求得在最大的线性隶属度λij下对应的最优解向量，运用FOWA算法解得不同专家对准则层指标的权重：

表2 专家1：评估指标比较判断矩阵

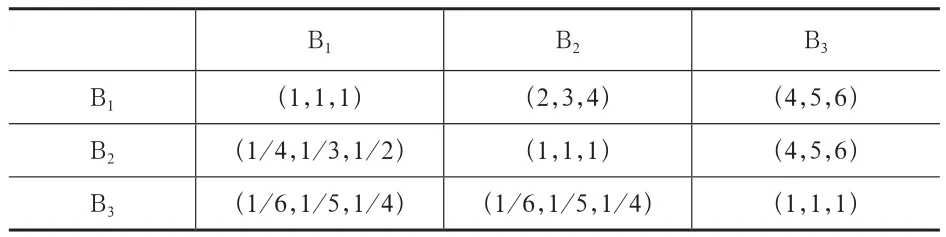
表3 专家2：评估指标比较判断矩阵

表4 专家3：评估指标比较判断矩阵

重复以上计算过程，得到控制系统失效、安全部件失效、振动舒适性差、噪声舒适性差4个元素层风险指标相对准则层各因素的权重值，见表5。通过模糊度排序方法进而求得各风险指标总体模糊权重值：即“安全部件失效”指标总体权重最大，应予以重点优先考虑。安全部件是电梯安全使用的最重要保护装置，在实际使用当中，直接影响使用者的生命安全。因此，该排序结果符合电梯实际运行情况。

表5 风险指标相对权重值

4 结论

考虑到老旧电梯运行失效因素的不确定性，本文从运行故障频率、日常运行管理、使用年限3方面对老旧电梯整机系统进行风险评价。传统层次分析法在计算权重时，如果一致性检验不通过，则需要专家重新打分构建判断矩阵，并再次进行一致性检验；如果准则层与元素层指标数量众多，且专家打分过于主观，可能导致一致性判断陷入死循环，评估过程无法进行下去。在三角模糊评价过程中，尽管仍然依赖专家打分构建三角模糊数构建评价矩阵，但是专家只需要对评估指标的判断进行模糊描述，评估过程中利用线性规划求解最优化解向量，不需要进行一致性检验。因此，有效解决传统层次分析法一致性检验不通过问题，并且保留了专家判断的差异性，即克服了判断的人为主观性。通过实例分析，评价结果符合实际情况，该方法是可行的。研究结果对于预先评判老旧电梯的运行安全性具有一定的指导意义。

[1]庆光蔚，岳林，胡静波.老旧电梯模糊定量安全技术评价方法研究[J].中国安全科学学报，2013，23(12)：126-131.

[2]门智峰，张彦朝.特种设备的风险评估技术[J].中国安全生产科学技术，2006，2(01)：92-94.

[3]范俊燕.基于机器学习的电梯安全评价研究[D].西安：西安工业大学，2011.

[4]徐泽水.基于FOWA算子的三角模糊数互补判断矩阵排序法[J].系统工程理论与实践，2003，23(10)：86-89.

[5]Dubios D，Prade H.Operations on fuzzy numbers[J].International Journal of Systems Science，1978， (09)：613-626.

[6]Mikhailov L. Deriving Priorities from Fuzzy Pairwise Comparison Judgements [J]. Fuzzy Sets and Systems，2003， 134(03)： 365-385.

[7]秦大力，张利，李吉慧.基于FAHP的信息安全风险评估方法[J].计算机工程，2009，35(15)：156-158.

Application of Triangular Fuzzy Extension Theory in Failure Probability Evaluating of Old Elevator

Ma Xingfu
(Elevator Engineering Institute, Hunan Electrical College of Technology Xiangtan 411101)

In order to accurately determine failure possibility of old elevator, a risk assessment method was established by using triangular fuzzy theory and analytic hierarchy process, which expanded the evaluation dimension and overcame the traditional evaluation bias. Firstly, the evaluation model was established from three aspects of fault frequency, daily operation management and service life. And the judgment matrix was established through the triangular fuzzy number to establish two pairs of triangular fuzzy judgment by the experts. Finally, the fuzzy weight was calculated by linear weighting method and the fi nal weight of the evaluation index was obtained. The results show that the risk of failure of the safety components is the biggest and should be paid more attention to and which veri fi es the feasibility of the method.

Triangular fuzzy number Old elevator Analytic hierarchy process Risk evaluation

X941

B

1673-257X(2017)09-0039-04

10.3969/j.issn.1673-257X.2017.09.008

马幸福（1983～)，男，硕士，讲师，工程师，从事特种设备系统安全分析研究工作。

马幸福，E-mail： maxingfu3618@163.com。

湖南省教育厅2016年科学研究资助项目（编号：16C0361）。

2017-03-16）