感生电场中导体回路间的电势差

洪 波 于正荣

(1. 江苏省盐城中学，江苏 盐城 224005 2. 盐城市伍佑中学，江苏 盐城 224041)

·问题讨论·

感生电场中导体回路间的电势差

洪 波1于正荣2

(1. 江苏省盐城中学，江苏 盐城 224005 2. 盐城市伍佑中学，江苏 盐城 224041)

变化的磁场产生感生电场,此电场分布于整个空间,导体回路处于感生电场中产生感生电动势．本文针对一道电磁感应习题,指出中学阶段常见解答中的科学性错误,并定量计算了区域为正方形的变化磁场所激发的感生电场,从而正确求出导体回路中的两点在感生电场中的电势差．

电磁感应;感生电场;电动势

1 问题的提出

题目.轻质细线吊着一边长为L=0.8m、匝数n=10的正方形线圈,R1=R2=R3=1Ω,其他电阻不计．边长为L/2的正方形磁场区域对称分布在线圈下边的两侧,如图1(甲)所示,磁场方向垂直纸面向里,大小随时间变化如图1(乙)所示．求:

图1

(1) 2s时通过电阻R1的电流大小和方向.

(2) 2s时,C、D两点间的电势差大小是多少?

(3) 6s内通过电阻R1的电荷量q及电阻R1上产生的热量.

类似习题中学阶段也不少见．本题中的第(2)问,得到广大中学教师的热烈讨论,但结果莫衷一是．参考答案如下:

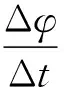
上述解答实际上存在一个重大的科学性错误．因为根据麦克斯韦电磁场理论,变化的磁场产生电场,这个感生电场通常构成闭合曲线,所以又称之为涡旋电场．并且此电场并不只仅仅处于有磁场的区域内,而是分布在包括磁场区域内、外的整个空间．本题尽管磁场限定于abcd内部,但abcd以外、线圈ABEF的四周都将存在感生电场．由于感应电动势就是由感生电场推动线圈内的自由电子移动引起的,因此线圈的4条边都可能存在电动势．所以,原参考答案仅仅把线圈的CD部分看成电源、其余部分看成外电路的处理方法是错误的．

上述观点得到绝大多数教师的肯定．但原题的结果究竟如何,大家无法确定．显然,要正确解答本题,首先要了解由于正方形区域内的变化磁场在空间所激发的的感生电场的分布情况,然后求出线圈ABEF各条边所产生的感应电动势,最后结合电路结构才能得出令人信服的结果．

2 有限区域的变化磁场所激发的感生电场

根据麦克斯韦方程,感生电场沿任何闭合路径的环流满足

∮lE·dl=-S·dS.

(1)

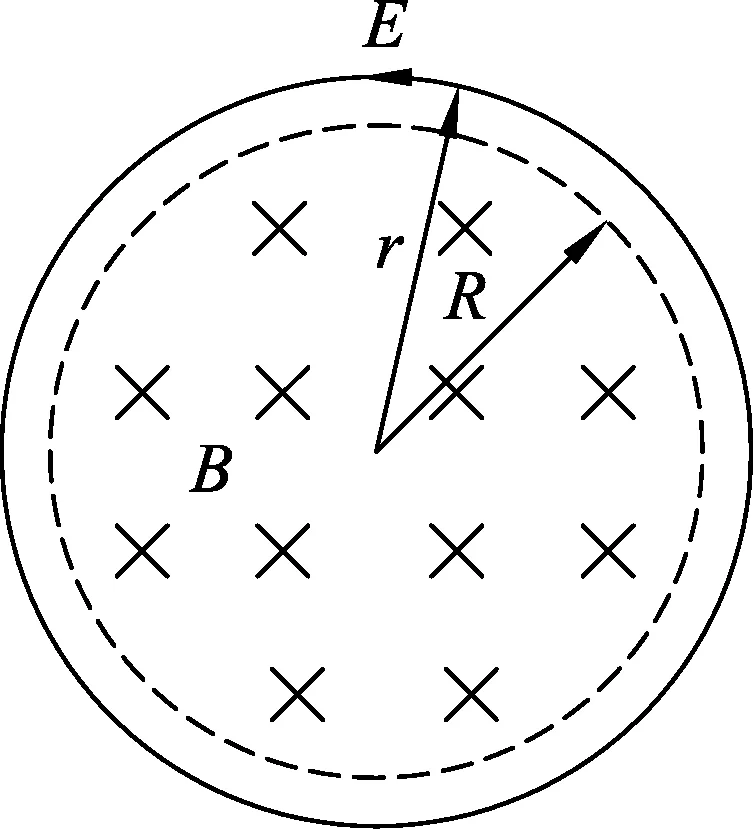
图2

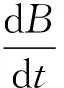
图3

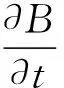
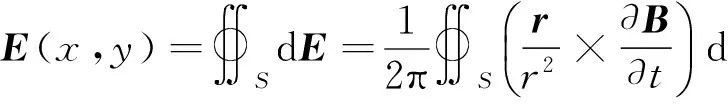
(2)

(2)式即为有限区域内随时间变化的磁场在周围空间所激发的感生电场的计算公式．其中位矢r的方向由Q指向P．

3 区域为正方形的磁场所激发的感生电场

图4

下面计算正方形磁场区域所激发的感生电场．设图1中正方形磁场区域abcd的边长为2a,以该正方形的中心O为坐标原点、bc方向为x轴正方向建立直角坐标系,如图4所示．在矩形磁场区域内取一面积元Q,其坐标为(x0,y0),面积为dS=dx0dy0．则Q到xy平面上任一点P(x,y)的位矢QP可表示为r=(x-x0)i+(y-y0)j．代入(2)式可得P点的感生电场为

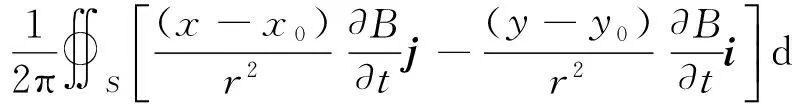
E(x,y)在x方向的分量为

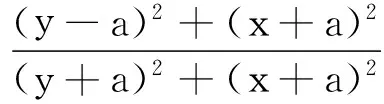
(3)

同理E(x,y)在y方向的分量为

(4)

考察(3)、(4)两式,不难发现该感生电场具有以下特点:

(1) 当x=0,y=0时,Ex=0,Ey=0．即坐标原点处无电场．当x=∞,y=∞时,Ex=0,Ey=0．即无穷远处感生电场也为0．

(2) 当x=0时,Ey=0,E=Ex,当y=0时,Ex=0,E=Ey．即x、y轴上各点的感生电场分别与x、y轴垂直．

(3) 此感生电场还具有下列对称关系.

Ex(x,y)=Ex(-x,y);Ey(x,y)=-Ey(-x,y)，

Ex(x,y)=-Ex(x,-y);Ey(x,y)=Ey(x,-y)，

Ex(x,y)=-Ex(-x,-y);

Ey(x,y)=-Ey(-x,-y).

即此感生电场以坐标原点O为对称点．

图5

通过数值计算模拟出此感生电场的电场线如图5所示,其形状类似圆形但不是圆形．

4 对原题的分析

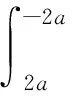
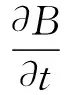
综上所述,由于磁场变化所激发的感生电场,不仅与磁场变化的快慢有关,还与磁场的区域(即边界条件)有关;除了圆形区域以外,其他形状的磁场所激发的感生电场的计算一般都非常复杂;由于感生电场分布在整个空间,我们可以通过其线积分来计算处于感生电场中的各部分导体产生的电动势,与法拉第电磁感应定律的结果一致,但具体计算远远超出中学内容的要求,所以在涉及相关内容的命题时一定要注意回避,更不可犯科学性错误．

1 桑芝芳.导体回路中的感应电动势是如何分布的[J].物理通报，2010(2)：8-11.

2 杨晓峰，许丽萍.变化磁场产生涡旋电场的一般形式[J].工科物理，1994(4)：4-5.

3 李卫平.涡旋电场的电场线总是圆形吗[J].中学物理，2012(23)：51-52.

4 赵坚.对涡旋电场中所谓“引入”电势、电势差概念问题的讨论[J].物理教师，2009(10)：6-7.

2017-02-27)