四面体单元剖分下三维各向异性TI介质中多次波射线追踪

2017-10-23李兴旺白超英李晓玲

石油地球物理勘探 2017年1期

关键词：群速度四面体对称轴

李兴旺白超英*② 李晓玲

（①长安大学地质工程与测绘学院地球物理系，陕西西安710054；②长安大学计算地球物理研究所，陕西西安710054；③国家知识产权专利局专利审查协作河南中心，河南郑州450000）

·地震模拟·

四面体单元剖分下三维各向异性TI介质中多次波射线追踪

李兴旺①白超英*①②李晓玲③

采用不规则四面体单元做模型剖分，实现了三维复杂层状各向异性TI介质中多次（透射、反射及转换）波的追踪计算，弥补了现行算法主要采用规则网格计算多次波的不足。根据介质的5个弹性参数及其对称轴倾角和走向，计算主节点上qP、qSV和qSH波群速度，由此线性插值得到次级节点的群速度值；然后采用不规则最短路径算法，并结合分区多步计算技术实现多次波追踪计算。均匀各向异性介质中计算出的数值解与解析解吻合，验证了算法的有效性。复杂层状模型数值模拟结果表明：采用不规则四面体单元可有效拟合起伏地表及地下不规则速度间断面，同时该算法适用于任意倾角的TI介质，且不受各向异性强度限制。

三维各向异性TI介质改进型最短路径算法多次波射线追踪四面体单元分区多步计算技术

1 引言

地球内部地层普遍存在各向异性现象，地震波在其中传播时，运动学和动力学属性均会发生明显改变，最为突出的是地震波速度的各向异性，即地震波速度不但与空间位置有关，而且与传播方向有关。当地层的各向异性不可忽略时，采用基于各向同性的方法来处理地震数据，将带来较大的计算误差，降低资料的解释精度，严重时可能得到错误的解释。因此，研究各向异性介质中地震波的传播规律显得尤为重要。早期研究大多针对具有垂直对称轴的VTI介质以及水平对称轴的HTI介质［1-5］。然而，实际地层更为复杂，例如褶皱和上冲等作用使地层发生倾斜、变形，介质对称轴也将发生变化，即不再是垂直或水平。此时，简单的VTI或HTI介质的假设难以满足地震勘探的实际要求。因此，有必要研究具有倾斜对称轴的TTI介质模型。

以往各向异性介质中的射线追踪，主要是在弱各向异性的假设条件下，采用传统算法（如打靶法或弯曲法）进行初至波追踪计算［6-11］。若介质较为复杂或讨论强各向异性介质时，上述方法将不再适用（出现“偏靶”或陷入局部解）。近年来出现的基于网格（或单元）波前扩展的算法（有限差分解程函方程法、最短路径算法、波前构造法等），由于其计算的稳健性、全局解、精度高、耗时少等优点，得到了广泛应用［12-17］。但此类研究依然局限于对初至波的讨论。另外，多数算法采用规则网格（或单元）进行模型参数化，不易处理起伏地表和地下复杂波阻抗界面，所以当模型复杂时存在较大计算误差。为了弥补以上缺陷，同时讨论一般各向异性介质中多次波的追踪计算，已实现分区多步不规则最短路径算法下的2D／3D各向异性TTI介质中多次波的追踪计算（简称 Multistage ISPM_TTI）［18］，以及三角网格剖分下二维各向异性TTI介质中多次波的追踪计算（简称 Multistage TSPM_TTI）［19］。本文则是将四面体单元剖分下各向同性介质中的多次波计算方法（简称 Multistage TSPM_3D）［20，21］推广至一般各向异性TTI介质中，从而实现含起伏地表（包括地下不规则界面）三维各向异性TTI介质中多次波地震射线的追踪计算。该算法采用不规则四面体单元做模型剖分，能更精确地拟合实际地学模型，适用于一般各向异性介质，主要难点是网格剖分和TTI介质各方向上相、群速度的计算，包括qSV波在奇异点出现多值时的处置。

2 TTI介质中相速度和群速度的计算

各向异性介质中相、群速度发生分离（图1），射线沿群速度方向传播，故将Multistage TSPM_3D算法推广到各向异性介质时，关键步骤是计算群速度。

图1 三维各向异性TTI介质相、群速度示意图

为了计算TTI介质的相、群速度，通常的做法是首先得到VTI介质中相速度的精确表达式，然后再经过坐标旋转得到TTI介质的相、群速度计算式。Daley等［22］给出了VTI介质中相速度的精确表达式，它仅依赖于以下5个弹性参数

式中：c1、c2、c3分别表示qP、qSV 和qSH 波的相速度；υ为入射角；（a11，a13，a33，a55，a66）是介质的五个弹性参数，且随位置坐标变化。

根据相、群速度的关系［23］（下标m=1，2，3分别对应三种类型的波，即qP、qSV和qSH），可得

上述讨论得到了VTI介质中群速度的计算方法，为了计算有任意倾斜对称轴的TTI介质，需将介质对称轴旋转一定角度（θ0，φ0）。对于某特定的相速度角（θ，φ），存在

将其代入式（1）～式（3），即可得到TTI介质中群速度值，其中相位的传播方向为

射线的传播方向是

另外，特殊（奇异值）点上的qSV波会出现三重值，此时宜选择群速度值中的最小值进行计算［14］。

3 四面体单元剖分下的最短路径算法原理

3.1 散点集四面体单元网的生成

近十几年来，散点四面体剖分一直是众多学者研究和关注的焦点。到目前为止出现了不少算法：Dwyer［24］提出 Voronoi图法；Radovitzky 等［25］则采用逐点插入法；郭际元等［26］给出了三种建立四面体网格的算法；孔娟华等［27］则是在Delaunay四面体的基础上提出了递推生成算法。本文将二维三角网格生长算法［20］推广到三维情形，形成的四面体满足空球准则，很好地解决了四面体不相容问题。图2给出了四面体网格剖分的示意图，为了成图清晰，仅给出模型3个表面（未标出次级节点）的分布情况。

3.2 模型参数化及界面离散

对于三维模型，按照各区界面的起伏情况采用不规则四面体单元对模型进行网格剖分（图2），四面体单元的4个角点为主节点（图3a），四个面上插入等间距的次级节点（图3b），四面体内部无节点（炮点和检波器可位于其内）。根据速度界面的具体情况，将其离散化，界面上离散点的间距应与四面体单元面上次级节点的间距相当。速度采样在主节点上，次级节点和界面离散点的速度值可通过线性插值获得［20，21］

图2 含起伏界面的三维层状模型中反射、透射、转换波计算示意图

图3 四面体内速度插值示意图

式中：v j表示i节点所在单元各主节点的速度值；uj为体积坐标。图3a中P点在四面体T1T2T3T4内的体积坐标u1可定义为：u1=V PT2T3T4／V T1T2T3T4，其中V PT2T3T4、V T1T2T3T4分别表示四面体PT2T3T4和T1T2T3T4的体积，对于u2、u3、u4，依此类推。

3.3 波前计算和射线追踪原理

分区多步计算方法是追踪多次波的核心。结合模型的起伏地表及波阻抗界面的几何形态、位置，将模型划分成多个相对独立的层状起伏区域。在射线追踪过程中，可根据多次波的类型进行分区多步计算，即确定每一步计算时的计算区域和调用相应的速度模型。由于每一步计算仅针对确定区域，规避了“无用区域”（射线不需要通过区域），在很大程度上减少计算时间和内存。对于大型三维模型，该优势尤为突出。

具体来讲，自震源所在的单元开始计算各节点的最小旅行时，该单元所有节点的旅行时计算结束后，进行波前扩展，直到该区域内所有节点均获得最小旅行时。此时波前停留在该区的速度离散界面上，同时保存速度界面上各离散点的旅行时和相应的射线路径。然后按照所要追踪的射线类型选择下一个区域进行计算，直至追踪到检波器为止。图2所示的多次波射线路径（红线）为P1SV2P2SV2P2P1（这里规定上标代表上行波，下标代表下行波，数字1、2表示分区号，另外，为了方便起见，这里P表示qP；SV表示qSV；SH表示qSH），采用上述原理可获得更为复杂多次波的射线路径和相应旅行时，技术细节可参见文献［18-20］。

3.4 节点旅行时计算方法

由于单元网格间距较小，相邻点间速度差异不大，对于i点附近任意节点j处的旅行时（可仅限于相同单元，也可仅限于相邻单元，参见文献［20，21］，即采用一阶或二阶Forward Star计算技术），可由以下公式（两点间距离除以平均群速度）近似计算

式中：i是波前面上当前的次级震源；j为将要计算的节点；Cj是j邻近节点的集合；是自炮点到达i节点射线的最小旅行时，其中m=1、2、3分别对应qP、qSV和qSH 三类波；D（X i，X j）是节点i与节点j之间的距离；和分别是i和j节点的群速度值。

当模型参数（a11，a13，a33，a55，a66，θ0，φ0）不随空间坐标变化时，即为均匀各向异性介质，U m只是（θ′，φ′）的函数。由公式（5）可得到等时面解析解，即Δt时刻沿（θ′，φ′）方向的一点到坐标原点的距离R（θ′，φ′），可确定该时刻等时面上的一个波前点（θ′，φ′，R（θ′，φ′））。当θ′、φ′分别取遍［0°，180°］、［0°，360°］各值时，可以得到完整的 Δt时刻的等时面（解析解）

4 实例模拟和结果分析

4.1 群速度与相慢度角和射线角的关系

为直观显示TI介质中群速度随相慢度角、射线角的变化情况，选择一组弹性参数（a11=5.2，a13=0.93，a33=4.0，a55=1.0，a66=1.0），分别针对VTI（θ0=0°），HTI（θ0=90°），TTI（θ0=45°）介质进行了试算。图4左图显示群速度随相慢度角的变化情况，右图为群速度随射线角的变化情况（从上到下θ0依次为0°、45°、90°）。从图4可见，qSV波群速度随射线角变化时出现了多重值现象，即同一射线角对应多个群速度值，这是Multistage TSPM_3D算法不能处理的，故应选择最小速度值进行计算以保证速度的连续性。而群速度与相慢度角的关系则是单一的，并没有出现多重值现象。同时，注意到qSH波群速度为常数，这是因为a55=a66=1.0。

图4 对称轴角度不同时三种波（qP、qSV和qSH）的群速度随相慢度角（左）及射线角（右）变化曲线

4.2 TTI介质群速度分布

采用Thomsen［28］给出的一组TTI模型参数（a11=25.7，a13=15.2，a33=15.4，a55=4.2，a66=9.0，θ0=45°和φ0=315°），计算得到t=1.0s时qP、qSV、qSH三种波等时波前的解析解（或称群速度分布图，图5a～图5c）和数值解（图5d～图5f）。从图5中可以看出，三类波群速度分布与该点和对称轴之间的夹角有关，在垂直于对称轴的平面内均为常量，但由于介质的各向异性，三类波都有着各自独特的波前面或群速度空间分布形态，尤其是qSV波的解析波前发生了分裂，沿对称轴方向及其垂向均出现了三重值（或重叠）现象。由于数值解仅使用qSV波最小速度进行计算，其结果并无波前分裂及三重值现象发生。

图5 TTI介质中qP、qSV、qSH波（从左到右）在t=1.0s时刻的等时波前

4.3 计算精度分析

为验证算法的有效性，选取Thomsen的Clay Shale模型（a11=15.1，a13=1.6，a33=10.8，a44=3.1，a66=4.3）构建均匀各向异性模型。模型尺寸为10km×10km×5km，炮点位于x轴中间点（5km，0，0）处。图6左右两部分分别给出了（θ0=0°，φ0=0°）和（θ0=45°，φ0=0°）时，x-z和x-y剖面上qP、qSV和qSH的等时波前，图中黑色为解析解，红色为数值解。为清晰起见，图中数值解时间间隔是解析解的一半。可见因群速度差异，三类波都有各自独特的波前面，且波前随介质对称轴倾斜方向不同而变化，亦证明群速度大小与介质对称轴的倾角有关。同时还发现qSV数值解中未出现解析解中的蝴蝶结（多重值）现象，这是由于数值算法无法使用多个群速度值来进行射线追踪造成的（只取了多重值中的最小群速度值进行计算）。除了蝴蝶结处外，其余部分数值解与解析解相吻合，甚至在蝴蝶结附近也非常一致。

4.4 复杂TTI介质中多次波追踪

本文所提算法可用于复杂TTI介质中多次波追踪，为使展示结果清晰明了，数值模拟时采用层状模型。选择如图7所示的三维层状起伏模型：模型尺寸为80km×80km×50km；地表起伏，最大起伏幅度为2km；在25km深度处有一个凹陷反射界面，最大凹陷幅度为4km；底部倾斜反射界面位于47～50km深度处。炮点位于（40km，40km，10km）的位置（图7中黑色圆点），31个检波器以等间距（8.0km）分布在模型地表的三条边上（图7中灰色圆点）。第一层模型参数为：a11=15.1，a13=1.6，a33=10.8，a55=3.1，a66=4.3，θ=φ=0°第二层模型参数为：a11=6.3，a13=2.25，a33=4.51，a55=1.0，a66=1.5，θ0=45°，φ0=315°。图7a展示了一次反射的情形，震相分别为P1P1、P1P2P2P1，即自炮点激发的P波经第一、二层起伏界面的反射波。图7b给出了多次透射、反射及转换波的射线路径：第一个震相为P1SV1P1，炮点激发的P波上行至地表，经反射并转换成SV波后下行至第一层反射界面，再次反射并转换成P波上行至检波器；第二个震相为P1SV1P2SV2P1，炮点激发的P波上行至地表，经反射转换为SV波后下行至第一层反射界面，透射且转换成P波后继续下行至第二层反射界面，然后反射转换成SV波上行至第一层反射界面，最后透射转换成P波上行至检波器。

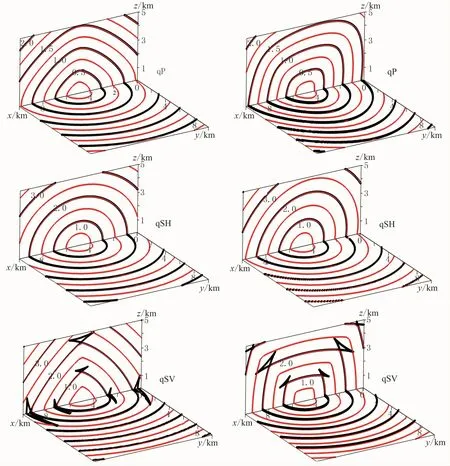
图6 基于三维Clay Shale模型的qP、qSV、qSH波在x-z和x-y剖面上的等时波前

图7 一次反射波P1 P1（蓝线）和P1 P2 P2 P1（红线）射线路径（a）、多次反射（转换）震相P1 SV1 P1（蓝线）和P1 SV1 P2 SV2 P1（红线）射线路径（b）

5 结论

本文将用于三维各向同性介质中的Multistage TSPM_3D算法推广至三维各向异性介质中，实现了三维TTI介质中多次（透射、反射、转换）波的追踪计算（简称：Multistage TSPM_3D_TTI算法）。该算法适用于任意倾角的TTI介质，且不受各向异性强度（即无弱各向异性的假设）的限制，可应对各类复杂介质；由于模型剖分时采用了不规则四面体单元，对起伏地表和速度间断面的拟合更加精确，能够处理各种复杂层状模型；同时，分区多步计算技术的采用，可实现复杂多次波的追踪计算。数值模拟验证了该算法的有效性和准确性，表明该算法具有较高的计算精度。下一步研究的重点则是利用这些多震相旅行时数据进行各向异性参数（其中包括倾斜对称轴）的反演。

［1］ Červeny V.Seismic rays and rays intensities in inhomogeneous anisotropic media.Geophysical Journal of Royal Astronomic Society，1972，29（1）：1-13.

［2］ Babich V M.Ray method of calculating the intensity of wavefronts in the case of a heterogeneous，anisotropic，elastic medium.Geophysical Journal International，1994，118（2）：379-383.

［3］ Cardarelli E，Cerreto A.Ray tracing in elliptical anisotropic media using the linear traveltime interpolation method applied to traveltime seismic tomography.Geophysical Prospecting，2002，50（1）：55-72.

［4］ Qian J，Symes W W.Finite-difference quasi-P traveltimes for anisotropic media.Geophysics，2002，67（1）：147-155.

［5］马德堂，朱光明.横向各向同性介质中初至波的旅行时计算.石油地球物理勘探，2006，41（1）：26-31.Ma Detang，Zhu Guangming.Calculating traveltime of the first arrival in transversely isotropic medium.OGP，2006，41（1）：26-31.

［6］ Grechka V Y，Mc Mechan G A.3-D tow-point ray tracing for heterogeneous，weakly transversely isotropic media.Geophysics，1996，61（6）：1883-1894.

［7］ Psencik I，Farra V.First-order ray tracing for qP waves in inhomogeneous weakly anisotropic Media.Geophysics，2005，70（6）：D65-D75.

［8］ Červeny V，Firbas P.Numerical modelling and inversion of traveltimes of seismic body waves in inhomogeneous anisotropic media.Geophysical Journal Royal Astronomical Society，1984，76（1）：41-51.

［9］ Gajewski D，Psencik I.Computation of high-frequency seismic wavefields in 3-D laterally inhomogeneous anisotropic media.Geophysical Journal Royal Astronomical Society，1987，91（2）：383-411.

［10］ Shearer P M，Chapman C H.Ray tracing in anisotropic media with a linear gradient.Geophysical Journal International，1988，94（3）：575-580.

［11］ Farm V.First-order ray tracing for qS waves inhomogeneous weakly anisotropic media.Geophysical Journal International，2005，161（2）：309-324.

［12］张中杰，何樵登.各向异性介质中折射波及其走时曲线研究.西安石油学院学报，1992，7（3）：1-6.Zhang Zhongjie and He Qiaoden.The study of refracted wave and its traveltime curve in anisotropic medium.Journal of Xi’an Petroleum Institute，1992，7（3）：1-6.

［13］赵爱华，张美根，丁志峰.横向各向同性介质中地震走时模拟.地球物理学报，2006，49（6）：1762-1769.Zhao Aihua，Zhang Meigen，Ding Zhifeng.Seismic traveltime computation for transversely isotropic media.Chinese Journal of Geophysics，2006，49（6）：1762-1769.

［14］ Zhou B，Greenhalgh S.On the computation of elastic wave group velocities for a general anisotropic medium.Journal of Geophysics and Engineering，2004，1（3）：205-215.

［15］ Zhou B，Greenhalgh S.Shortest path＇ray tracing for most general 2D／3D anisotropic media.Journal of Geophysics and Engineering，2005，2（1）：54-63.

［16］ Zhou B，Greenhalgh S.Raypath and traveltime computations for 2D transversely isotropic media with dipping symmetry axes.Exploration Geophysics，2006，37（2）：150-159.

［17］马德堂，朱光明，范廷恩.二维TTI介质中初至波旅行时的搜索算法.石油地球物理勘探，2011，46（5）：710-714.Ma Detang，Zhu Guangming，Fan Ting’en.Search algorithm of first arrival traveltime in 2D TTI medium.OGP，2011，46（5）：710-714.

［18］ Bai C Y，Huang G J，Li X L et al.Ray tracing of multiply transmitted／reflected／converted waves in 2D／3D layered anisotropic TTI media and application to crosswell traveltime tomography.Geophysical Journal International，2013，195（2）：1068-1087.

［19］李晓玲，白超英，胡广义.起伏层状TI介质中多次波射线追踪.石油地球物理勘探，2013，48（6）：924-931.Li Xiaoling，Bai Chaoying，Hu Guangyi.Multiple ray tracing in an undulated layered TI media.OGP，2013，48（6）：924-931.

［20］ Bai C Y，Li X L，Tang X P.Seismic wavefront evolution of multiply reflected，transmitted，and converted phases in 2D／3D triangular cell model.Journal of Seismology，2011，15（4）：637-652.

［21］ Bai C Y，Li X，Wang Q L，Peng J B.Multiple arrival tracking within irregular triangular or tetrahedral cell model.Journal of Geophysics and Engineering，2012，9（1）：29-38.

［22］ Daley P，Hron F.Reflection and transmission coefficients for transversely isotropic media.Bulletin of the Seismological Society of America，1977，67（3）：661-675.

［23］ Berryman J G.Long-wave elastic anisotropy in transversely isotropic media.Geophysics，1979，44（5）：896-917.

［24］ Dwyer R A.Higher-dimensional voronoi diagram in linear expected time.Discrete and Computational Geometry，1991，6（4）：64-67.

［25］ Radovitzky R，Ortiz M.Tetrahedral mesh generation based on node insertion in crystal lattice arrangements and advancing-front-Delaunay triangulation.Computer Methods in Applied Mechanics and Engineering，2000，187（3-4）：543-569.

［26］郭际元，龚俊芳.由三维离散数据生成四面体网格算法研究.中国地质大学学报（地球科学），2002，27（3）：271-273.Guo Jiyuan，Gong Junfang.Algorithms of producing tetrahedral network from three dimensional dispersed data.Journal of China University of Geosciences（Earth Science），2002，27（3）：271-273.

［27］孔娟华，郑江滨.一种三维离散点数据生成结构四面体算法.计算机工程与科学，2009，31（1）：35-37.Kong Juanhua，Zheng Jiangbin.An algorithm of generating unstructured tetrahedrons from 3D discrete points.Computer Engineering and Science，2009，31（1）：35-37.

［28］ Thomsen L.Weak elastic anisotropy.Geophysics，1986，51（10）：1954-1966.