基于RACA算法快速计算导体RCS

陈 磊，陈业慧，金 建

(安徽新华学院 电子通信工程学院，安徽 合肥 230088)

基于RACA算法快速计算导体RCS

陈 磊，陈业慧，金 建

(安徽新华学院 电子通信工程学院，安徽 合肥 230088)

针对传统矩量法庞大的求逆运算、超长的计算时间等问题，提出了一种研究电磁散射特性的新思路.该方法首先应用自适应交叉近似算法求解阻抗矩阵，再利用奇异值分解方法进一步压缩此阻抗矩阵，从而加快矩阵运算并节省存储量，数值计算结果表明该方法精确、有效.

自适应交叉近似算法；再压缩技术；雷达散射截面

矩量法(method of moments，MoM)[1]是分析目标电磁散射特性的经典方法，优势包括计算精度高、适应范围广、不易产生数值色散.随着电磁兼容领域的不断发展，目标散射体的尺寸和材料变得庞大、复杂，导致计算机内存和处理速度难以满足要求，传统矩量法的弊端开始显现.为了快速求解目标雷达散射截面，常采用傅里叶变换法(fast Fourier transform，FFT)[2]、自适应积分法(adaptive integral method，AIM)[3]和快速多极子算法(fast multipole algorithm，FMA)[4]等，但傅里叶变换法和自适应积分法用于表面积分方程的效果较差，快速多极子算法求解阻抗矩阵时需要已知的格林函数.

自适应交叉近似算法(adaptive cross approximation algorithm，ACA)[5-6]是一种纯数学方法，通过压缩方式快速求解矩阵元素且不依赖格林函数与积分方程.文献[7-9]提出了再压缩自适应交叉近似算法(recompressed adaptive cross approximation algorithm，RACA)，它在ACA算法的基础上，进一步对阻抗矩阵分解压缩，使计算时间和内存消耗显著减少.

1 理论分析

1.1阻抗矩阵方程

当入射场Ei照射理想导体时会产生电场作用力，导体内部电荷在该力的作用下开始移动，在表面S上形成电流，称为感应电流J，进而生成新的电场，称为散射场Es.根据麦克斯韦电磁理论对理想导体表面总电场强度切向分量的描述可知:

-Es(r)|tan=Ei(r)|tan，r∈S.

(1)

表面S上的感应电流J应用RWG[10]基函数{fn(r)}展开，权函数为{gm(r)}，由伽略金法将式(1)转成矩阵方程:

Z(k)·I(k)=V(k).

(2)

式中：Z(k)代表阻抗矩阵；I(k)为待求电流；V(k)表示激励.依据矩量法原理和文献[7]所述方法，可快速求解阻抗矩阵元素Zm×n.

1.2自适应交叉近似算法

ACA算法充分体现了数学原理.由于远场阻抗矩阵Zm×n是低秩矩阵，故可以用两个满秩矩阵的乘积形式表示，实现阻抗矩阵的压缩，近场部分用矩量法填充元素.

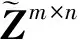
(3)

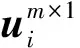
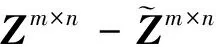
(4)

终止迭代 .其中，ε为误差迭代门限，‖×‖是矩阵的Frobenus范数.

ACA算法的自适应原则确保了Um×t和Vt×n求解时，只要计算矩阵中的t行和t列即可，不必算出每个元素.从而，阻抗矩阵元素填充数目减至t×(m+n)，计算复杂度也随之降低.

1.3再压缩技术

ACA算法生成的两个矩阵Um×t和Vt×n为非正交阵，存在冗余成分，常采用奇异值分解方法除之.为了保证高精确度和易操作的需求，忽略低奇异值，选择高奇异值及其对应的奇异分量构造低秩矩阵.具体步骤如下：

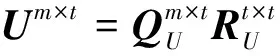
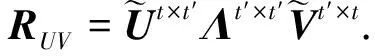
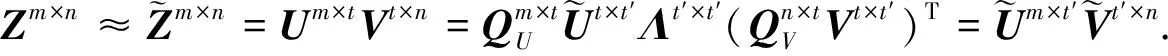
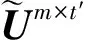
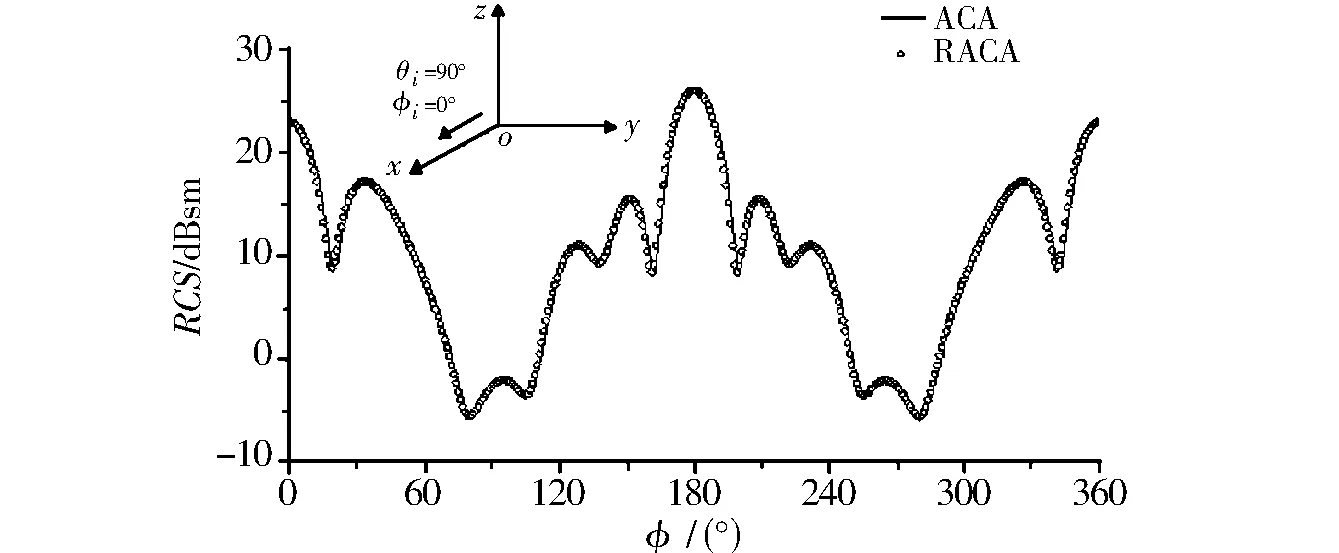
图1 导体立方体的双站RCSFig.1 Bistatic RCS of a conducting cube

2 数值结果分析

算例均在CPU为2.97 GHz，RAM为2 GB 的计算机上完成，采用Fortran语言编程，ACA算法和奇异值分解门限均为0.001.

算例1 计算边长为1 cm的导体立方体的双站RCS.入射频率为40 MHz，入射角θi=90°，fi=0°.经过三角单元剖分，得到800个单元数、1 160个未知变量.ACA与RACA计算出的双站RCS曲线如图1所示.

算例2 研究导体球双站RCS.圆球半径为1 cm，入射频率为400 MHz，入射角θi=90°，φi=0°.经过三角单元剖分，得到3 600个单元数、5 400个未知变量和56个非空组.ACA与RACA计算出的双站RCS曲线如图2所示.

算例3 分析组合台状导体的双站RCS.入射频率为100 MHz，入射角θi=0°，φi=90°.经过三角单元剖分，得到2 908个单元数、4 362个未知变量和52个非空组.ACA与RACA计算出的双站RCS曲线如图3所示.

图3 导体组合体的双站RCSFig.3 Bistatic RCS of a conducting combination object

从图1至图3可看出，两种算法的结果吻合度较高.3个算例的CPU计算时间和内存消耗情况如表1所示.由此可见，RACA更省时间和内存.

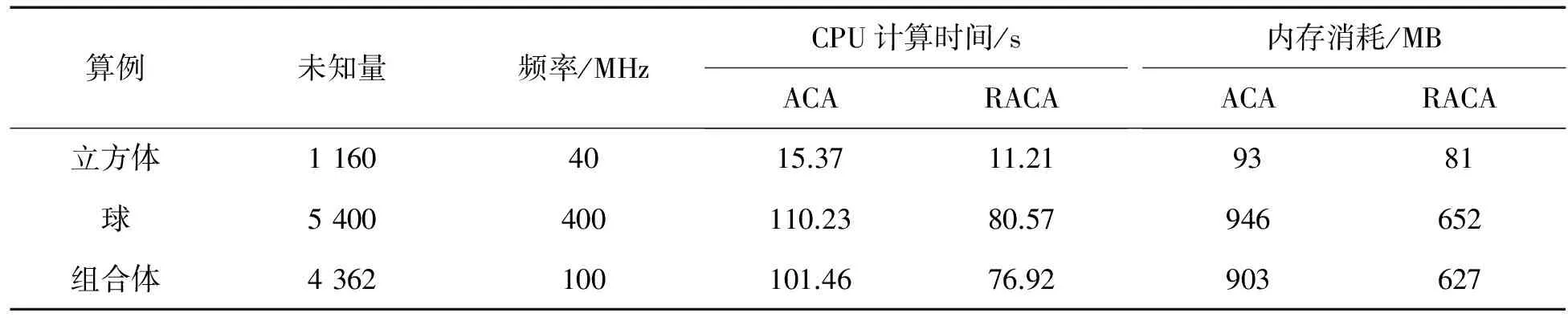
表1 CPU计算时间与消耗内存比较Tab.1 The comparison of CPU time computation and memory consumption

3 结语

本方法应用RACA加速求解导体RCS，在计算阻抗矩阵元素的过程中，通过不断减少满秩矩阵的秩实现存储少、耗时短的目标，从而提高了计算效率.

[1] HARRINGTON R F.Field Computation by Moment Method[M].New York:Macmillan,1968:22-57.

[2] 徐岩,张晓明，王瑜.基于离散傅里叶变换的频谱分析新方法[J].电力系统保护与控制，2011，39(11)：38-43.

[3] 王兴，龚书喜，关莹，等.AIM结合渐近波形估计技术快速分析目标宽带电磁散射特性[J].电子与信息学报，2011，33(8)：1975-1980.

[4] 丁振宇，洪伟.快速多极子在任意截面均匀介质柱散射中的应用[J].电波科学学报，2010，25(1)：127-131.

[5] 姚雨帆，孙玉发，王仲根，等.应用EDM法和ACA算法快速计算电大开缝导体RCS[J].合肥工业大学学报(自然科学版)，2014，37(4)：440-443.

[6] SUI M,XU X J.Angular glint calculation and analysis of radar targets via adaptive cross approximation algorithm[J].Journal of Systems Engineering and Electronics,2014,25(3):411-421.

[7] BEBENDORF M,KUNIS S.Recompression techniques for adaptive cross approximation[J].Journal of Integral Equations and Application,2009,21(3):331-357.

[8] KAZEMPOUR M,GUREL L.Fast solution of electromagnetic scattering problems with multiple excitations using the recompressed adaptive cross approximation[C]∥IEEE Antennas and Propagation Society International Symposium,Memphis：IEEE Computer Society,2014:745-746.

[9] HELDRING A,UBEDA E,RIUS J M.On the convergence of the ACA algorithm for radiation and scattering problem[J].IEEE Transactions on Antennas and Propagation,2014,62(7):3806-3809.

[10]RAO S M,WILTON D R,GLISSON A W.Electromagnetic scattering by surfaces of arbitrary shape[J].IEEE Transactions on Antennas and Propagation,1982,30(3):409-418.

FastcalculationoftheRCSofconductingobjectsbasedonRACAalgorithm

CHENLei,CHENYehui,JINJian

(CollegeofElectronicCommunicationsEngineering,AnhuiXinhuaUniversity,Hefei230088,China)

In order to solve the problems of large inverse operations and time consumption, a new solution is proposed to analyze the electromagnetic scattering characteristics. Firstly, the adaptive cross approximation(ACA) algorithm is applied to calculate impedance matrix. Then, the singular value decomposition is applied to compress the impedance matrix got from ACA algorithm. The aim is to accelerate matrix calculation and reduce matrix storage. The numerical results illustrate the efficiency and accuracy of the proposed method.

adaptive cross approximation algorithm; recompressed technique; radar cross section

TN011

A

1674-330X(2017)03-0050-03

2017-03-25

安徽省高校自然科学研究项目(KJ2016A306)

陈磊(1990-)，男，安徽舒城人，助教，硕士，研究方向为无线通信与电磁兼容.