不同铺层角度下CFRP薄壁箱梁几何非线性特性试验分析
2017-10-23赵玉如冯荣贞
赵玉如,皇 民,冯荣贞
(河南工程学院 土木工程学院,河南 郑州 451191)
不同铺层角度下CFRP薄壁箱梁几何非线性特性试验分析
赵玉如,皇 民,冯荣贞
(河南工程学院 土木工程学院,河南 郑州 451191)
工程结构受到各种外界因素的影响,常出现几何非线性效应.在这种情况下,传统结构内力及挠度计算常被简化成线性,导致计算结果偏差较大,影响结构安全.复合材料纤维的走向在很大程度上影响结构的力学性能,通过试验的方法研究了不同纤维铺层角度时,碳纤维复合材料CFRP薄壁箱梁在几何非线性效应下的力-位移曲线的变化规律.结果表明,当宽跨比一定时,90°铺层的箱梁挠度最大,0°铺层对应最小,而且90°铺层的箱梁力-位移变化幅度显著,几何非线性特征明显.
CFRP薄壁箱梁;几何非线性;纤维铺层角度
碳纤维复合材料CFRP具有强度高、自重小、耐久性强、安全性高、便于施工等优点,被广泛应用在桥梁结构中[1],采用CFRP薄壁箱梁逐渐成为新型桥梁的发展趋势.传统的内力及挠度计算常将结构受力简化为线性,但实际上基本都是非线性的.本研究在相关试验的基础上,对CFRP薄壁箱梁几何非线性效应下的相关特性进行分析,以供结构设计和施工参考.
对于多层复合材料制作的薄壁箱梁来说,复合材料纤维的铺设角度对结构构件的几何非线性特征有很大影响. 王利霞等[2]做了CFRP薄壁箱梁抗弯性能试验,研究线性状态下箱梁力-位移曲线的变化趋势,表明只在竖向力作用下(结构线性)力-位移曲线是一条斜直线,此试验只考虑了简单荷载作用下箱梁小变形、小挠度的力学响应.但在实际工程中,结构构件常处于大变形、大挠度下,即呈几何非线性状态.杨东涛等[3-4]利用理论和有限元分析的方法研究了铺层角度对CFRP薄壁悬臂梁、简支梁、连续梁的扭转角、挠度、截面应力的影响规律.基于前人的基础,笔者在试验中研究薄壁箱梁在不同铺层角度时几何非线性效应的力-位移变化规律.
1 复合材料层合板
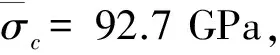
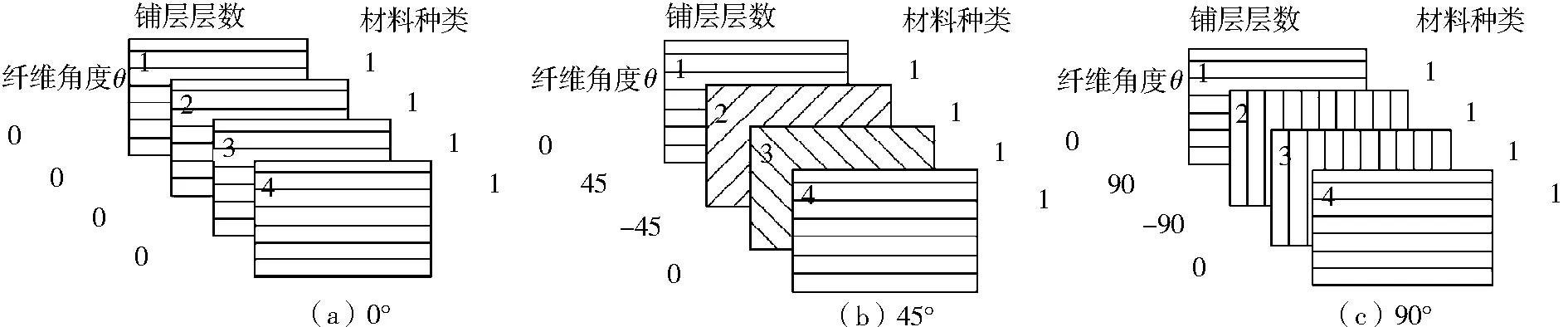
图1 层合板铺层角度示意图Fig.1 Schematic diagram of the plywood
2 不同铺层CFRP薄壁箱梁的非线性特性试验
2.1方案设计和试件制备
利用上述不同铺层的层合板制作3种薄壁箱梁(0°,45°,90°),箱梁截面尺寸同为36 mm×16 mm,跨度为450 mm,600 mm,800 mm,共9个模型,如图2和图3所示.
2.2试验试件的加载
试验加载装置如图4所示.箱梁跨中位置作用的竖向力p采用杠杆加载装置进行加载,梁两端截面位置作用的轴向力n,是利用滑轮将砝码竖向力转换而成的,加载过程中采用应变仪测定每一分级加载工况下跨中底板对应的应变值,用3个百分表分别测试每一工况下梁支座和跨中的位移(这里梁支座处设百分表是为了消除支座沉降的影响).
分别对梁长为450 mm,600 mm,800 mm,铺层角度为0°,45°,90°的梁进行加载试验.首先,对每个铺层的梁分别固定竖向力p=306n,然后对每种竖向力作用下的梁做轴向力n的分级载入:0n,10n,20n,30n,…,150n, 160n,165n,185n,207.1n,212.1n,对所有的梁进行加载.

图2 U型槽模型Fig.2 U-slot model

图3 应变片粘贴位置Fig.3 Strain plate affixed position

图4 箱梁加载装置Fig.4 Loading device of box girder
2.3试验数据的处理分析
图5给出了不同跨度下的梁在铺层角度不同时跨中挠度随荷载的变化曲线.

图5 不同跨度的梁在铺层角度不同时跨中挠度随荷载的变化曲线Fig.5 Curve of mid-span deflection with load in different span beams
由图5可知,3种跨度的箱梁均表现出了几何非线性特征,跨度一定时,不同铺层的箱梁跨中挠度随荷载呈曲线变化,表现出明显的几何非线性特征:0°铺层时力-位移曲线斜率变化缓慢,几何非线性特征表现弱,45°次之,90°时的挠度曲线变化幅度相对大,几何非线性最明显,这与文献[3]的结论一致.另外,由图5中的3个图对比可知,当铺层角度一定时,跨度越大,几何非线性特征表现得越明显.
上述结果表明,在工程中运用CFRP薄壁箱梁时,纤维的铺层角度对结构的受力特性有很大影响,要根据需要选择合适的黏结方式.
3 结语
CFRP薄壁箱梁在竖向力-轴向力共同作用下表现出明显的几何非线性特性,此时薄壁箱梁的力-位移关系不再呈直线变化,复合材料纤维的铺层角度对挠度有很大影响,0°时影响最小,45°次之,90°时影响最大,影响程度随角度的增加递增.在以后的设计和施工过程中,要综合考虑结构受力、施工难度与拟建桥梁的跨度,选择合适的复合材料纤维铺层角度.
[1] 曾宪桃,车惠民.复合材料在桥梁工程中的应用及前景[J].桥梁建设,2002(2):66-70.
[2] 王利霞,吴亚平,施琪,等.碳纤维箱形梁的剪力滞效应试验研究 [J].兰州交通大学学报(自然科学版),2009,28(4):1-3.
[3] 杨东涛,吴亚平,苏强.复合材料箱梁非线性分析的本构方程研究[J].兰州交通大学学报(自然科学版),2005,24(6):17-19.
[4] 李维东.复合材料连续箱梁及悬臂箱梁的剪力滞效应试验研究[D].兰州:兰州交通大学,2012.
[5] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.定向纤维增强聚合物基复合材料拉伸性能试验方法:GB/T 3354—2014[S].北京:中国标准出版社,2014.
[6] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.纤维增强塑料性能试验方法(总则):GB/T 1446—2005[S].北京:中国标准出版社,2005.
Thegeometricnon-linearityexperimentalanalysisofCFRPthin-walledboxgirderswithdifferentfiberlayingangles
ZHAOYuru,HUANGMin,FENGRongzhen
(CollegeofCivilEngineering,HenanUniversityofEngineering,Zhengzhou451191,China)
The geometrical non-linear effect often occurs in the engineering structure affected by various external factors. In the traditional theory,structural calculation get on under linear condition,the results will have greater error,which will affect the structural safety. The mechanical properties of structure will be effected when the fibers have different angle. According to experimental method and changing the different laying angle of fibers ,this paper gave force-displacement curve variety of CFRP thin-walled box girder in the geometrical non-linear effect .The results show that when the span ratio is constant, the deflection of the box with 90° is the largest, and the 0°is the smallest, and the force-displacement variation of the box with 90° is significant, and the geometrical nonlinearity is obvious.
CFRP thin-walled box girder; geometrical non-linear effect; fiber layer angle
TU33
A
1674-330X(2017)03-0037-02
2017-01-06
赵玉如(1986-),女,河南开封人,助教,硕士,主要从事桥梁新材料的研究.
