基于PSO的系统可变约束优化求解与仿真
2017-10-23翟红生
翟红生
(河南工程学院 计算机学院,河南 郑州 451191)
基于PSO的系统可变约束优化求解与仿真
翟红生
(河南工程学院 计算机学院,河南 郑州 451191)
针对化工过程存在可变、非严格刚性约束优化的问题,提出了一种基于命题转化和粒子群算法的系统可变约束优化求解方法.该方法首先将非刚性可变约束进行转化和处理,将其作为一个优化指标,然后将这个优化指标作为一个罚乘子与原优化目标组成一个新的综合优化目标.由此,原单目标优化命题就转变为多目标优化命题,并且利用PSO多目标优化算法对该多目标优化命题进行求解.同时,对求得的解进行优化,对可变约束范围进行理论分析,给出了在约束不定情况下合理可行的优化求解方案并进行了验证.结果表明,该方法应用于实际生产中是可行与有效的.
可变约束; 多目标;命题转化;优化求解;粒子群
过程系统优化尤其是化工过程系统优化往往具有一定的不确定性[1].随着设备的不断更新、生产状况的调整和市场行情的变化,优化条件和目标都会变化.为了适应这种变化,生产过程的优化往往具有一定的柔性,然而在长期的生产过程中,追求全局最优往往是不现实的[2].
在传统的优化过程中,优化命题和约束一般是刚性的,即过程系统模型和边界约束必须满足等式或者不等式的约束条件[3].如果在优化过程中得到的解无法满足约束条件,那么就无法得到优化解[4].上述方法仅仅考虑数学上的规划求解,并没有考虑实际过程中很多约束条件不是刚性的.
在化工过程系统中,软约束或可变约束是普遍存在的[5].考虑到反应过程参数的变迁和设计过程中预最优运行点的不确定性,优化过程将会包含较多的可变约束.因此,可变约束与设备的软约束有一定的不同,基于可变约束的优化命题求解需要合理的设计和优化求解方法[6].
基于集群智能的优化算法如遗传算法[7]、模拟退火算法[8]在化工生产过程中有着广泛应用,它们可求解全局最优解,并用于智能分类、路径规划等领域[9].但是,这类优化算法在一般约束过程中往往存在一定的难度,采用罚函数法时,罚乘子的选择对优化目标求解影响较大[10],特别是针对可变约束优化命题.
针对上述问题,粒子群优化算法在优化求解中有着高效和良好的求解能力,故很快被扩展到多目标优化求解中.本研究结合粒子群多目标优化的优势,根据可变约束优化命题求解的特点,提出了一种基于粒子群的可变约束优化方法,将其应用于化工过程优化设计和参数估计.通过某化工过程优化设计和参数估计命题进行实验验证,结果表明该方法应用于实际生产过程中是实用和有效的.
1 优化命题的分析与转化
对于过程系统而言,若变量上下界约束表示设备能力约束,目标函数一般表示生产效益,而约束方程表示变量取值的范围.如果采用数学规划形式的刚性优化命题,则优化命题可以表示为
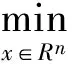
(1)
对于该优化命题形式,如果采用传统方法对其求解,得到的仅是一个严格的数学表达式.对于以上命题形式采用遗传算法等智能算法时,通常是通过加权罚乘子方法将其处理为无约束优化方法.然而,加权罚乘子的选择没有固定方法,不易选取且不具有普遍性,在约束条件较为复杂时,最优结果难以通过求解得到.
过程系统优化命题的实际情况是更多的约束均为软约束形式,即等式约束形式一般不要求严格满足,只要在设备、过程反应中满足一定的约束范围就可以了,所以考虑实际情况,优化命题形式可表示为如下形式:
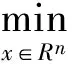
(2)
对于以上不等式约束形式,采用遗传算法更加难以求解,实际过程未必存在也未必非要得到优化命题的全局最优解.对于此类型的命题,可以通过一些转化手段,将其转化为多目标优化命题求解.对于式(1)表示的优化命题,通过添加松弛变量,将原命题中的不等式约束转化为等式约束.松弛变量为
(3)
h(x)+S=0,
(4)
将其并入等式约束中,则为以下形式:
(5)
同样,将式(2)转化为

(6)
对于δi进行归一化处理,具体方式如下:
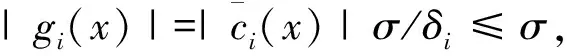
(7)
式中:σ为人工规定的容限误差.考虑到要对约束施加惩罚,故在目标函数中增加惩罚项.原问题转化为一个多目标优化形式:

(8)
对于以上多目标优化命题,只要最终优化点的‖g(x)‖≤σ,则该优化点就符合优化要求.而对于以上优化约束g(x),只要它不是过程约束,那么就应该能够得到满意解甚至全局最优解.当然,对于优化过程来说,当全局解与满意解相差很小时,全局解的意义也不是很大,实际运行中还要考虑全局最优解附近的鲁棒性等要求,所以只要得到很好的满意解就足够了.
以上优化命题为多目标优化命题,粒子群优化算法在求解这类命题时非常有效,所以对以上优化命题采用粒子群多目标优化方法求解.
2 基于PSO的系统可变约束优化求解
在1995年,Kenndy和Eberhart提出了粒子群优化(partical swarm optimization,PSO)算法[11].在PSO算法中,鸟群中的每一只鸟都是优化命题的潜在解,命名为粒子.PSO算法对群粒子进行随机初始化,然后对群体中的粒子进行迭代搜索,并求得其最优解.在对粒子进行迭代的过程中,PSO算法不断跟踪个体极值和群体极值来对自己的位置和速度进行更新.个体极值(pBest)是指粒子本身搜索到的最优解,全局极值(gBest)是指群体搜索到的最优解.2002年以后,粒子群优化逐渐扩展到多目标优化[12],并且其优化效率等优势得到了充分体现,越来越多的背影用于实际过程的多目标优化中.多目标粒子群优化基本算法如下:
(2)初始化种群的适应度
fori=1 ton
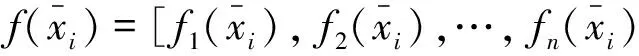
(3)根据Pareto概念,将开始的种群分成Pareto子集和N_Pareto子集,n1表示Pareto子集的大小,n2表示N_Pareto子集的大小,满足n1+n2=n(1≤n1,n2≤n).
(4)通过下式不断对N_Pareto子集内粒子的速度和位置进行更新,Vid=w×Vid+c1×rand()×(pid-xid)+c2×rand()×(pgd-xid),xid=xid+Vid.其中,pgd从Pareto子集中选取.
(5)动态交换策略
fori=1 ton2
对N_Paret子集和Pareto子集中的粒子进行比较;
如果N_Paret子集中的粒子比Pareto中的好,就将其进行互换.
(6)对Pareto子集、N_Pareto子集和n1,n2进行更新.
(7)假设n1≠n或者没有迭代到最大次数,就执行第(4)步.
对于式(8)形式的优化命题,可采用多目标优化算法进行优化计算.
3 仿真研究
本实验所使用的计算机CPU为酷睿2 E4300、主频为2.0 GHz、显存为1 GB.
3.1用于反应器设计优化
反应器的网络设计问题要求设计两个反应器容积,目标是使反应物B的浓度最大,模型描述为以下形式:
(1)目标函数为min-cB2.
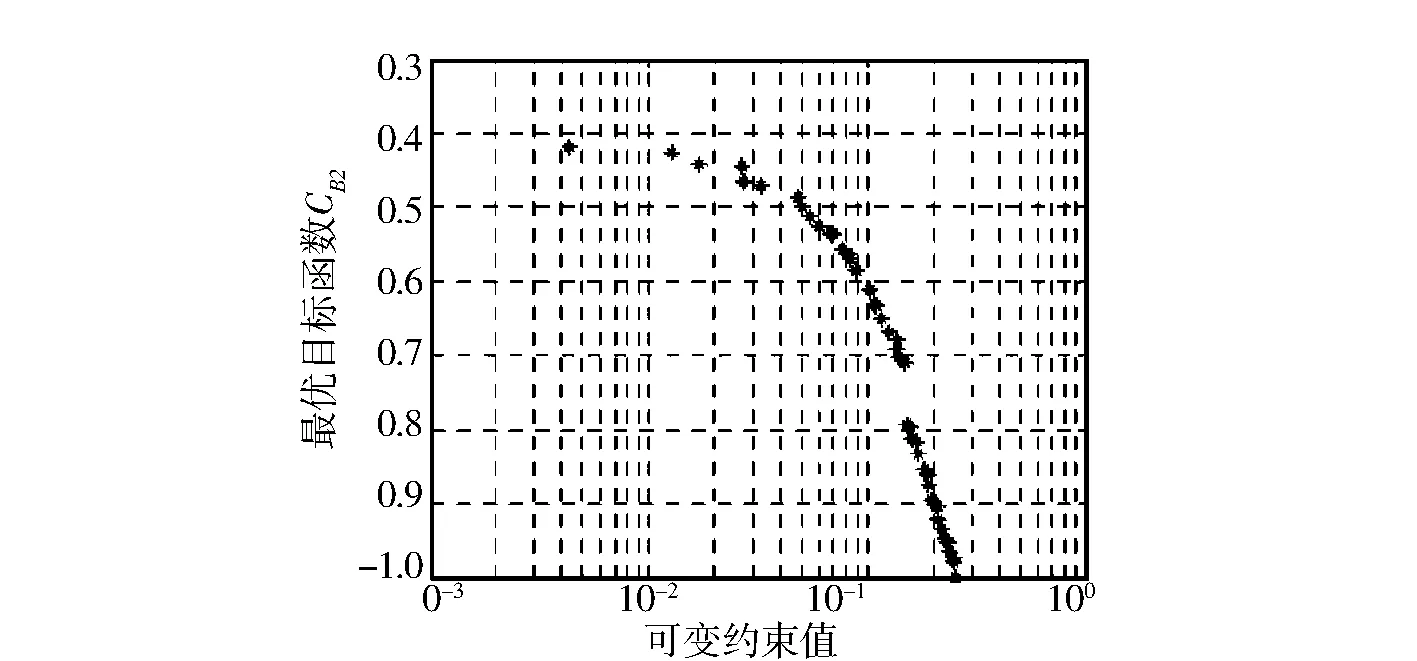
图1 可变约束与最优目标CB2的关系Fig.1 Relationship between variable constraints and optimal objective CB2
考虑到反应速率常数与反应状况、辨识方法有关,以上等式约束方程在实际过程中并不严格满足,只要残差不太大就行.约束方程中的不等式约束表示两个反应器的总容积小于一定范围,这里考虑了反应器的成本,容积越大,反应器的制造成本也越高.实际上,不等式约束也是软的约束.
对于以上优化命题,采用优化求解方法求解.粒子种群为45,在150代以内完成优化求解,得到的结果如图1至图3所示,图中的横坐标均表示约束可变的范围.
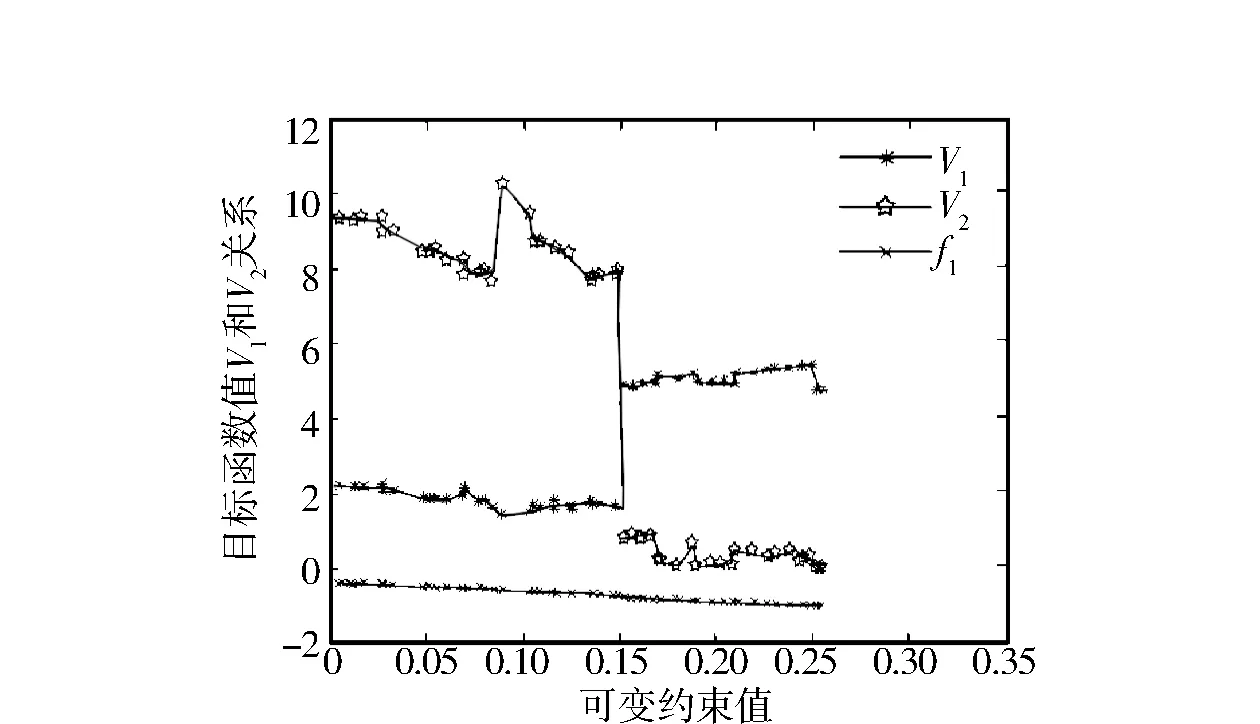
图2 可变约束值与V1和V2的关系Fig.2 Relationship between variable constraint values and V1 and V2
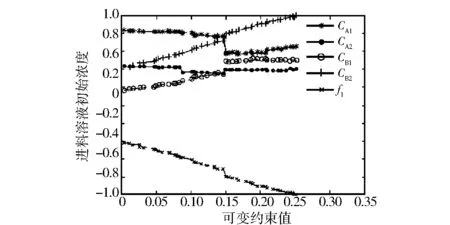
图3 可变约束与初始浓度选择的关系Fig.3 Relationship between variable constraints and initial concentration
图1表示可变约束值与最优目标函数值的对应变化关系,其中最优目标函数值即原命题的目标函数值.可变约束的区间范围越大,目标函数值越小,反应物B的浓度越高.命题中进入反应器的浓度变化是造成约束变化的原因之一,造成约束波动较大的另一因素是反应系数与温度、浓度、设备变化都有关系.与波动造成约束变化对应的是目标函数值会在相应的范围内变化.在这种情况下,如何设计反应器的容积对目标函数值有较大影响.
图2表示可变约束范围与反应器容积的关系.为了方便起见,目标函数值也放在图2中.从图2可以看出,在可变约束区间小于0.15时,反应器容积分别为9和2,当可变约束大于0.15时,反应器容积发生跳变,进料溶液浓度也发生了跳变,情况如图3所示.根据以上情况,反应器容积设计可选择可变约束小于0.15的优化值,这时优化目标值对反应器容积的灵敏度不高且优化区间具有很好的稳定性.
3.2用于参数估计
该优化命题描述如下:
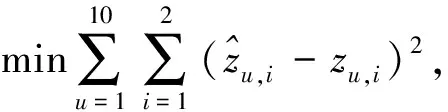
观测数据如表1所示.
对该命题采用本方法进行优化计算.采用粒子种群为45,在150代内完成计算,计算结果如图4和图5所示.图4表示可变约束变化与目标函数值之间的关系,其中的目标函数值为原命题的优化目标函数值,不含有乘子项.随着约束可变区间变大,最优目标值变小,趋向于更优.在一定的约束可变范围,以上优化结果均比较合理.
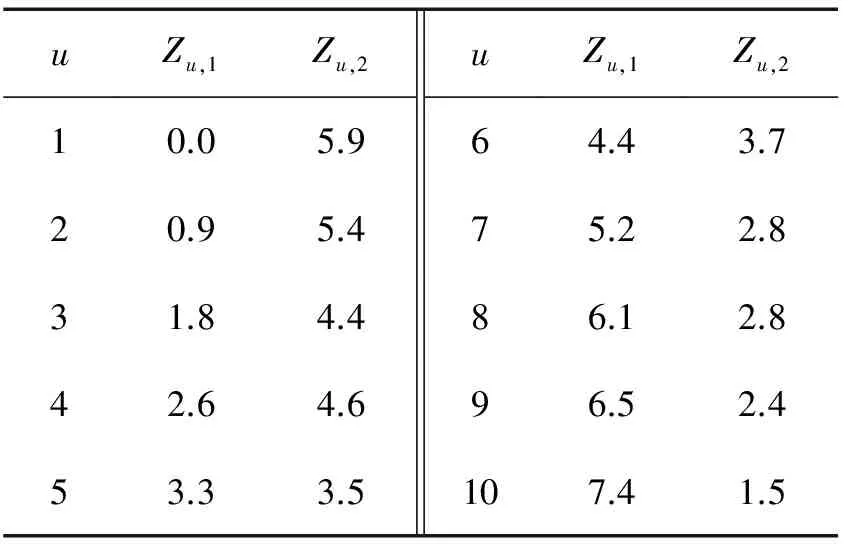
表1 观测数据Tab.1 Observed data
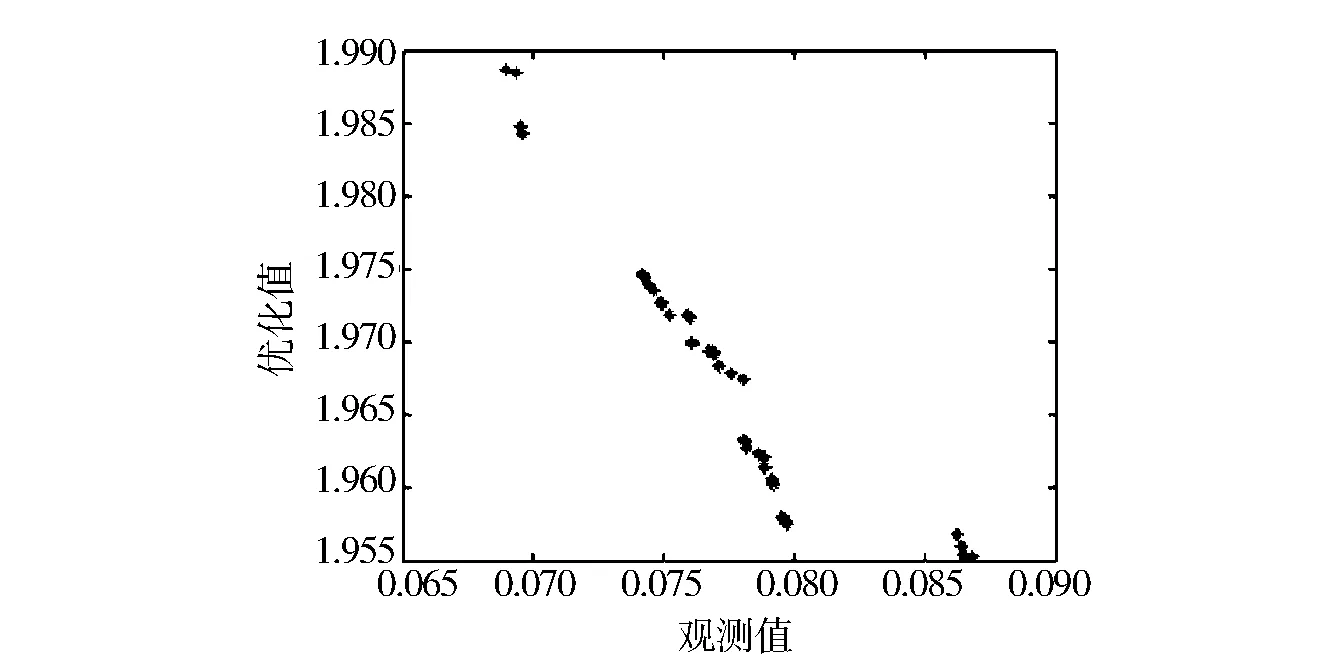
图4 可变约束与最优目标值的关系Fig.4 Relationship between variable constraints and optimal target values
如图5所示,将在约束变化值为0.068 9、目标函数值为1.988 8的情况下得到的优化值与观测值进行比较.Zu,1*,Zu,2*表示得到的优化值,Zu,1,Zu,2表示观测值,从图5中看出,观测值与优化值总体上比较符合.
图6表示可变约束与参数θ1,θ2的关系.从图6中可以看出,当可变约束为0.065~0.090时,θ1和θ2值变化很小,几乎稳定在某个值.在θ1和θ2的整个波动范围内,任选一组参数均可认为是满足目标要求的最佳参数值.

图5 某可变约束下优化数据与观测数据的比较Fig.5 Comparison between optimized data and observed data under a variable constraint
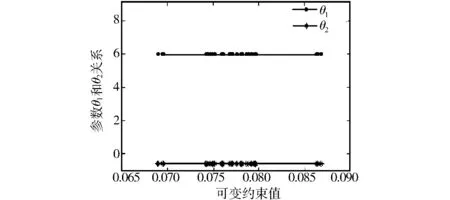
图6 可变约束与参数θ1和θ2的关系Fig.6 Relationship between variable constraint and parameter θ1 and θ2
4 结语
对于过程系统尤其是化工过程系统优化而言,优化过程往往具有一定的不确定性.随着设备的不断更新、生产状况的调整和市场行情的变化,优化条件和目标都必须有相应的变化,在生产过程中对优化条件的要求往往具有一定的柔性.为了解决该类具有不确定性因素的约束有一定可变范围的最优化命题,本研究根据实际生产要求,将这类优化命题转换为一种多目标优化命题,并采用PSO算法对其进行求解和分析,提出了一种基于命题转化和粒子群算法的系统可变约束优化求解方法.同时,对化工优化设计和参数估计的两个优化命题进行了优化求解和分析,结果表明该方法是有效的.
[1] 刘伟,蔡前凤,刘海林.基于参数方程处理等式约束优化的粒子群算法[J].计算机工程与设计,2012,29(3):697-699.
[2] 徐迅,鲁海燕,徐向平.基于环形邻域拓扑的自适应速度PSO算法[J].计算机工程与应用,2015,51(18):32-37.
[3] 许君,鲁海燕,石桂娟.限制速度粒子群优化和自适应速度粒子群优化在无约束优化问题中的应用[J].计算机应用,2015,35(3):668-674.
[4] VOROZHEIKIN A Y,GONCHAR T N,PANFILOV I A,et al.A modified probabilistic genetic algorithm for the solution of complex constrained optimization problems[J].International Conference on Machine Learning & Cybernetics,2015,11(5): 113-119.
[5] 胡良臣,寿华好.PSO求解带法向约束的B样条曲线逼近问题[J].计算机辅助设计与图形学学报,2016,28(9): 1443-1450.
[6] CHEN W N,ZHANG J,CHUNG H S,et.al.A novel set-based particle swarm optimization method for discrete optimization problems[J].Evolutionary Computation,IEEE Transactions on Evolutionary Computation,2012,14(2):278-300.
[7] KHOSA F K,ZIA M F,BHATTI A A.Genetic algorithm based optimization of economic load dispatch constrained by stochastic wind power[C]∥International Conference on Open Source Systems & Technologies,IEEE,Lahore:International Conference on Open Source Systems & Technologies,2016:36-40.
[8] 陈伟,贾立.间歇过程PSO-SQP混合优化算法研究[J].仪器仪表学报,2016,37(2):339-347.
[9] SIVARANJANI P,HEMALATHA R.Optimization of constraint based non-slicing VLSI floorplan using hybrid cuckoo search and genetic algorithm[J].International Journal of Applied Engineering Research,2015,10(20):18793-18798.
[10]符强,汪鹏君,童楠,等.基于MODPSO算法的FPRM电路多约束极性优化方法[J].电子与信息学报,2017,39(3):717-723.
[11]LIU L,YANG S,WANG D.Particle swarm optimization with composite particles in dynamic environments[J].Systems,Man,and Cybernetics(Part B):Cybernetics,IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society,2012,40(6):1634-1648.
[12]于双双,王铁宁,可荣博,等.基于改进PSO的装备维修器材调剂供应决策[J].计算机工程与应用,2015,51(22): 258-266.
SolutionandsimulationofsystemvariableconstraintoptimizationbasedonPSOalgorithm
ZHAIHongsheng
(CollegeofComputer,HenanUniversityofEngineering,Zhengzhou451191,China)
In order to solve the problem of variable and non-rigid constraint optimization in chemical process, a variable constraint optimization method based on propositional transformation and particle swarm optimization (PSO) is proposed and the simulation is conducted. The method firstly treated non-rigid variable constraint and transformed it as an optimization index, then the optimization index as a penalty multiplier and the original optimization objective formed a new integrated optimization. Thus, the single objective optimization is turned into a multi-objective optimization proposition, and the PSO multi objective optimization algorithm is used to solve the multi-objective optimization problems. At the same time, the solution is optimized and the variable constraint range is theoretically analyzed. A reasonable and feasible optimization solution under the constraint is given and verified. The result shows that this method is feasible and effective in actual production process.
variable constraint; multi-objective; proposition conversion; optimization; particle swarm
TP273
A
1674-330X(2017)03-0060-05
2017-03-21
翟红生(1975-),男,河南巩义人,讲师,主要从事计算机应用技术研究.
