饱和土体中线弹性连续屏障的隔振分析
2017-10-23丁海滨杨园野徐长节童立红赵秀绍
丁海滨,杨园野,徐长节,2,童立红,赵秀绍
(1.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室,南昌 330013;2.浙江大学 滨海和城市岩土工程研究中心,杭州 310058)
饱和土体中线弹性连续屏障的隔振分析
丁海滨1,杨园野1,徐长节1,2,童立红1,赵秀绍1
(1.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室,南昌 330013;2.浙江大学 滨海和城市岩土工程研究中心,杭州 310058)
基于Biot波动理论,推导了饱和土中S波入射线弹性固体连续屏障时反射P1波、P2波、S波的反射系数与透射S波、P波的透射系数的解析解。进行算例分析,得出各反射透射系数与线弹性固体连续屏障密度、泊松比及弹性模量的关系。结果表明:线弹性固体隔振结构密度对P1波和P2波反射系数基本无影响;而随着线弹性固体隔振结构密度的增大,S波的反射和透射系数及P波的透射系数均逐渐减小,且渐趋稳定;线弹性固体连续屏障泊松比和弹性模量的变化对P1波P2波反射系数及P波透射系数基本无影响,而对S波的反射系数和透射系数影响较大,S波的反射系数随着线弹性固体连续屏障的泊松比和弹性模量的增大而增高,S波的透射系数随着泊松比的增大而减小,随着弹性模量的增大而增大。
振动与波;S波;饱和土;隔振屏障;反射系数;透射系数
环境振动危害的防治一直是工程中不可忽视的问题,关于波的传播,振动的隔离,已有诸多学者进行了研究。Biot基于饱和土的双相介质特性,最先提出了“多孔介质变形”理论,讨论了饱和土中三种波的传播,并给出了饱和土体各参数的物理意义及测量方法[1–2]。叶成江等通过理论推导结合算例分析研究了入射角度、入射频率、及界面透水条件对S波(secondary wave)由饱和土入射弹性土时的反射和透射系数的影响[3]。周新民等采用理论推导结合算例分析研究了饱和土中P波(Primary wave)入射水气界面时与入射角及频率的关系[4]。Lin着重研究了孔隙率对平面波在饱和土体中的反射的影响[5]。高广运基于薄层法原理推导了饱和地基的三维动力基本解答,研究了轨道交通荷载作用下饱和地基波阻板主动隔振的规律[6]。
屏障隔振有排桩,填充沟墙,空沟等多种形式,研究主要分为现场试验,理论研究,数值模拟三个方面。Woods通过大量试验研究,提出了有关屏障隔振设计的基本准则,并提出振幅衰减系数作为隔振衡量标准[7]。Takemiya提出了蜂窝形柱状屏障,并通过现场试验验证了其隔振效果[8]。理论研究方面,陈元杰基于Biot理论与半解析法研究了单排桩对低频振动的隔振效果[9]。徐平等运用复变函数的保角映射方法和波场势函数展开法研究了多排屏障对P波的隔离效果[10]。高广运等研究了层状地基屏障隔振问题,分析了排桩桩长和不同桩土剪切模量比对排桩隔振效果的影响[11]。Aviles采用波函数展开法研究了各种波入射情况下排桩的隔振效果[12]。徐斌等根据饱和土Biot理论,分析了空沟对移动荷载引起饱和土体振动的被动隔振效果[13]。袁万等基于Biot饱和多孔介质理论,采用Galerkin法和Fourier变换,研究了均质和层状饱和土中,空沟的隔振效果[14]。数值模拟方面,朱兵见等采用有限元-无限元解法分析了沟深、沟宽及空沟到振源的距离对空沟隔振效果的影响[15]。
以混凝土为代表的线弹性固体材料作为建筑隔振屏障材料,在工程中应用广泛。对于饱和土体中线弹性固体连续屏障的隔振效果,诸多学者进行了实验研究和数值模拟研究,然而基于理论推导的数值解析研究尚较少见。因此研究线弹性固体连续屏障的材料参数对于隔振效果的影响,对于环境振动危害的防治具有重要意义。
1 饱和土波动方程
根据Boit波动理论,波动方程表述为[1]:
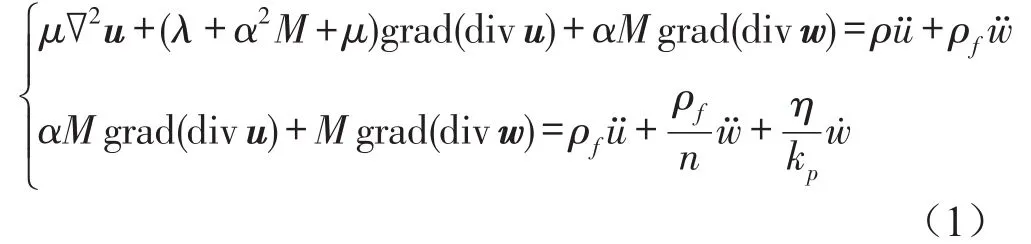
饱和土为固液两相介质,可设其位移势函数由标量势φs,φf和旋转势ψs,ψf组成,其中下标s表示土体骨架,f表示液体。故可将土骨架位移和流体相对位移与势函数写成
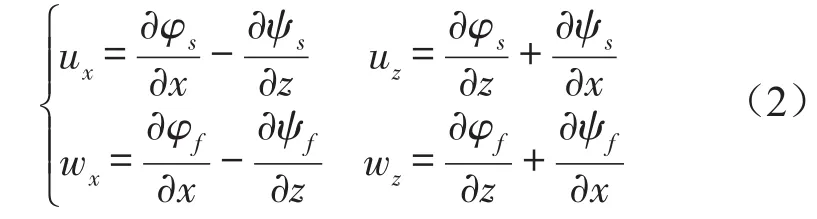
设平面波解的形式为
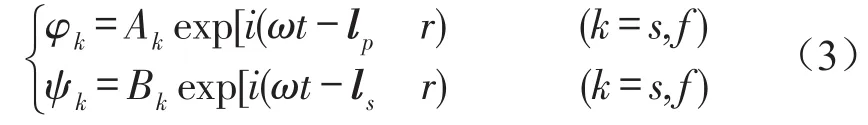
其中Ak,Bk——分别为P波和S波幅值;
将式(2)、式(3)代入式(1)中,对式(3)进行解耦,由非零解的条件可得到频散方程[4]
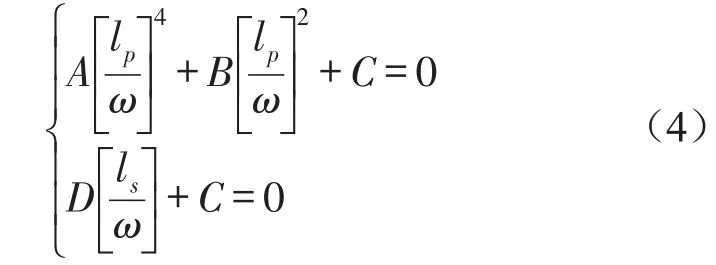
其中A=(λ+2μ)·M

其中ω——入射波频率;
lp1,lp2,ls——波矢量;
λ,α,μ,M,η——土体模量;
解得三个波矢量值lp1,lp2,ls,证实饱和土中存在三种波P1,P2及S波,并得到饱和土体中流体和固体各自势函数幅值的比值为[4]
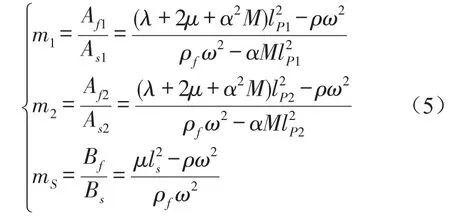
ρ——饱和土体密度。
2 反射与透射系数求解
工程中振害多由剪切波引起,选用S波为研究对象。取频率为ω的S波由饱和土入射线弹性固体连续屏障(如图1所示),入射角度、反射角度及透射角度如图中标示,则有
(1)饱和土体中(x<0)
入射S波势函数

反射P波势函数
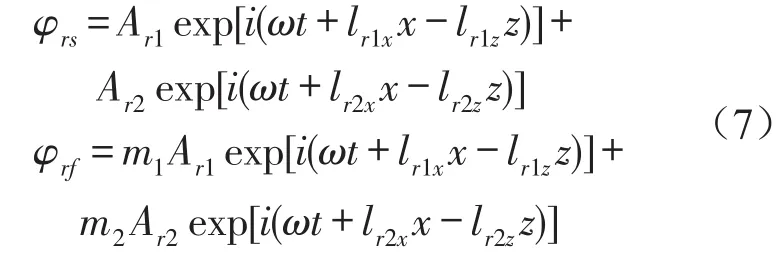

图1 S波由饱和土入射线弹性固体在界面上的反射与透射
反射S波势函数

(2)线弹性固体连续屏障中(x>0)
设线弹性固体连续屏障中位移与势函数关系

透射P波势函数

透射S波势函数

(3)边界条件

用势函数表达饱和土体的应力与流体压力
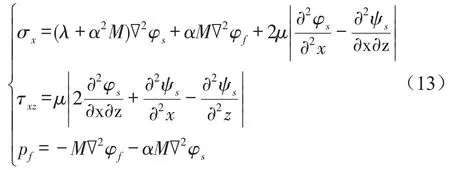
线弹性固体的本构方程

其中E,ν—线弹性固体弹性模量和泊松比;
用势函数表达线弹性固体的应力
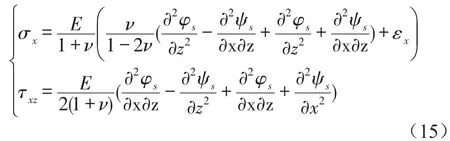
将势函数本构方程代入边界条件得系数矩阵

令Bis=1,解方程组(15)可得反射和透射系数Ar1,Ar2,Brs,Bts,Atp的解析解。
3 算例分析
本文通过数值算例,分析线弹性固体连续屏障密度、泊松比及弹性模量对反射与透射系数的影响。
(1)饱和土体参数的计算
采用的饱和土体参数见表1。
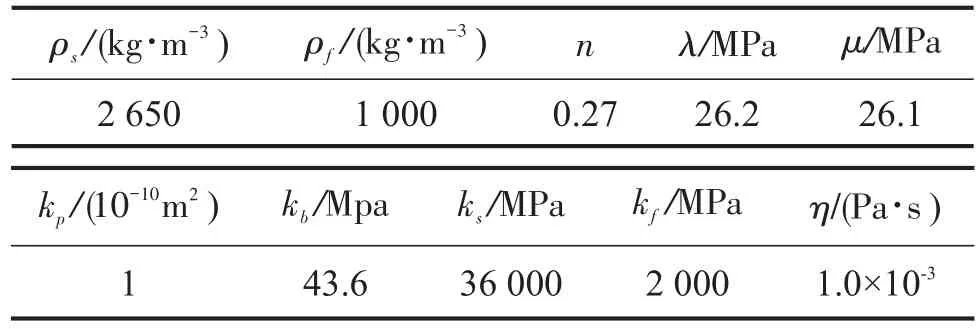
表1 饱和土体参数
代入式土体参数可得A、B、C、D值,将A、B、C与D值代入式(4)可解得lp1,lp2,ls值,将lp1,lp2,ls值代入式(5)可得饱和土体中固液势函数幅值得比值m1,m2,ms。
(2)线弹性固体参数的计算
故波数的数值满足

根据Snell折射定律有:
lissinαi=lrssinαi=lr1sinβ1=lr2sinβ2=ltssinαt=ltpsinβt换 算 可 得lisz,lis,lisx,lrs,lrsx,lr1,lr1x,lr2,lr2x,lts,ltsx,ltp,ltpx的值和表达式。将各参数代入Ar1,Ar2,Brs,Btp,Atp的解析解,即可得到Ar1,Ar2,Brs,Bts,Atp关于ω,α,ρ′,E,ν的表达式。
(3)线弹性固体密度对反射及透射系数的影响
令ω=100,αi=370,E=30 GPa,ν=0.1,分析了线弹性固体连续屏障密度为1 000 kg/m3到3 000 kg/m3时反射系数与透射系数的变化情况,如图2所示。

图2 各波反射透射系数与线弹性固体密度关系
由图2可以看出,线弹性固体连续屏障密度从1 000 kg/m3变化到3 000 kg/m3时,S波反射系数从0.8降到0.15,S波透射系数从1.8降到0.2,P波透射系数从0.03变化到0.01,随着线弹性固体连续屏障的密度增加,S波的反射和透射系数及P波的透射系数均呈减小趋势;且由图可以看出随着线弹性固体连续屏障的密度的增大,S波的反射和透射系数及P波的透射系数渐趋稳定。
线弹性固体连续屏障的密度对P1波和P2波反射系数基本无影响,对S波的反射和透射系数及P波的透射系数影响较大。饱和土和隔振屏障交界面上,旋转势能量较大,标量势能量较小,故线弹性固体隔振屏障密度的变化对反射P1波和P2波的的影响很小;随着线弹性固体隔振屏障密度的增加,反射的能量减小,故S波的反射系数会减小;同一种介质中,波的振幅越大能量往往越高,故随着线弹性固体隔振屏障密度增大,透射的能量有一定增加,但透射系数却逐步减小;随着线弹性固体隔振屏障密度的一直增加,入射能量的分配渐趋稳定,故S波的反射和透射系数及P波的透射系数也渐趋稳定。
(4)线弹性固体泊松比和弹性模量的影响
令ω=100、αi=370、ρ′=2 000 kg/m3,分析了线弹性固体连续屏障泊松比从0.1到0.3,弹性模量从10GPa到30GPa时反射系数与透射系数的变化情况,如图3到图7所示。
由图3和图4可以看出,S波入射线弹性固体时,在界面上反射P1波的反射系数随着线弹性固体连续屏障的泊松比和弹性模量的增大而降低,反射P2波的反射系数随着线弹性固体连续屏障的泊松比和弹性模量的增大而增大;当线弹性固体连续屏障泊松比从0.1变化到0.3,P1波和P2波的反射系数变化幅值为0.001左右;线弹性固体连续屏障的弹性模量从10GPa变化到30GPa时,P1波和P2波的反射系数变化幅值为0.004左右。说明线弹性固体连续屏障的泊松比和弹性模量变化,对P1波和P2波的反射影响不大。
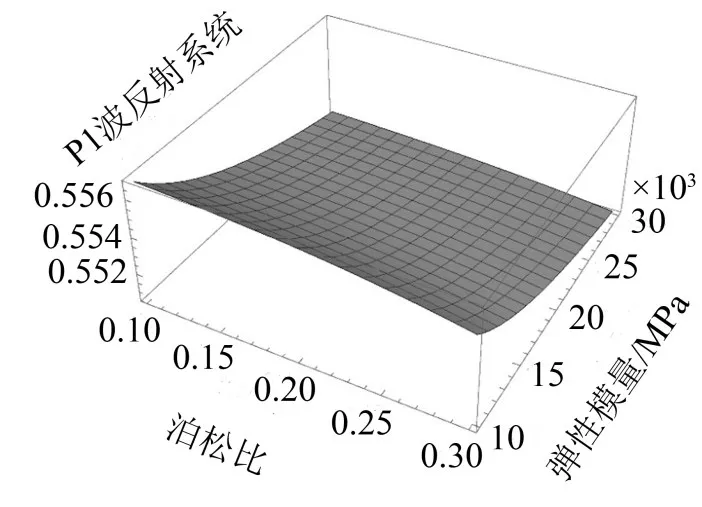
图3 P1波反射系数与线弹性固体参数关系

图4 P2波反射系数与线弹性固体参数关系
由图5可以看出,S波的反射系数随着线弹性固体连续屏障的泊松比和弹性模量的增大而增高,当线弹性固体连续屏障的泊松比从0.1变化到0.3,其变化幅值为0.02左右;线弹性固体连续屏障的弹性模量从10GPa变化到30GPa时,其变化幅值为0.09左右。说明线弹性固体连续屏障的泊松比和弹性模量变化,对S波的反射系数影响较大。

图5 S波反射系数与线弹性固体参数关系
由图6可以得到,P波透射系数随泊松比和弹性模量的增大而减小,当线弹性固体连续屏障的泊松比从0.1变化到0.3,其变化幅值为0.000 3左右;线弹性固体连续屏障的弹性模量从10GPa变化到30 GPa时,其变化幅值为0.000 7左右。说明线弹性固体连续屏障的泊松比和弹性模量变化,对P波的透射系数影响较小。
由图7可以看出,S波的透射系数随着泊松比的增大而减小,随着弹性模量的增大而增大,当线弹性固体连续屏障的泊松比从0.1变化到0.3,其变化幅值为0.15左右;线弹性固体连续屏障的弹性模量从10GPa变化到30GPa时,其变化幅值为0.2左右。说明线弹性固体连续屏障的泊松比和弹性模量变化,对S波的透射系数影响较大。

图6 P波透射系数与线弹性固体参数关系
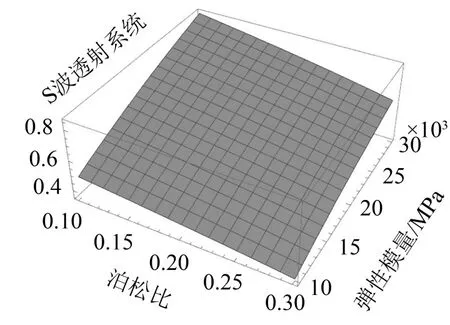
图7 S波透射系数与线弹性固体参数关系
同样的,饱和土和隔振屏障交界面上,旋转势能量较大,标量势能量较小,故线弹性固体泊松比和弹性模量的变化对反射和透射P波的的影响都很小。线弹性固体隔振屏障泊松比和弹性模量的变化引起旋转势和标量势能量的分配,引起反射系数与透射系数的变化。
4 结语
本文采用理论推导结合算例分析,研究了S波由饱和土入射线弹性固体连续屏障时,线弹性固体连续屏障密度,泊松比及弹性模量对反射波反射系数,透射波透射系数的影响。结果表明:
(1)线弹性固体隔振结构密度对P1和P2波反射系数基本无影响;随着线弹性固体隔振结构密度的增大,S波的反射和透射系数及P波的透射系数均逐渐减小,且渐趋稳定。
(2)线弹性固体连续屏障泊松比和弹性模量的变化对P1波和P2波的反射系数及P波透射系数基本无影响;对S波的反射系数和透射系数影响较大,S波的反射系数随着线弹性固体连续屏障的泊松比和弹性模量的增大而增高,S波的透射系数随着泊松比的增大而减小,随着弹性模量的增大而增大。
(3)为达到更好的隔振效果,应综合考虑采用密度小,弹性模量小,泊松比高的线弹性固体连续屏障。
[1]BIOT M A,mechanics of deformable and acoustic propagation in porous media[J].Reprinted from Journal ofApplied Physics,1961.33(4):1482-1498.
[2]MAURICE A BIOT.Theory of propagation of elastic waves in a fluid-saturated porous solid.I.Low frequency range[J].The Journal of the Acoustical Society of America,1956.28(2):168-178.
[3]叶陈江,史焱永,蔡袁强.波由饱和土入射于弹性土时在界面上的反射与透射[J].振动与冲击,2005(2):41-45+147.
[4]周新民,夏唐代,徐平,等.饱和土介质中地震波在水、气分界面上的反射与透射[J].地震学报,2006,25(4):372-379+450.
[5]LIN CHI-HSIN,VINCENT W LEE,MIHAILO D TRIFUNAC.Thereflection ofplane wavesin a poroelastic half-space saturated with inviscid fluid[J].Soil Dynamics and Earthquake Engineering,2005.25(3):205-223.
[6]高广运,王非,陈功奇,等.轨道交通荷载下饱和地基中波阻板主动隔振研究[J].振动工程学报,2014(3):433-440.
[7]WOODS R D.Screening of surface waves in soils[J].Am.Soc.Civil Engr.J.Soil Mech,1968,94(4):951-979.
[8]HIROKAZU TAKEMIYA.Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct[J].Soil Dynamics and Earthquake Engineering,2004.24(1):69-87.
[9]陈元杰.移动荷载引起饱和土动力响应及排桩隔振-基于饱和土体Biot理论与半解析法分析[J].江西建材,2016(5):12-13.
[10]徐平,邓亚虹,吴明.饱和土体中多排桩屏障对压缩快波的隔离[J].工程力学,2014(5):120-127.
[11]高广运,李佳,李宁,等.三维层状地基排桩远场被动隔振分析[J].岩石力学与工程学报,2013(S1):2934-2943.
[12]JAVIER AVILÉS FRANCISCO J SÁNCHEZ-SESMA.Foundation isolation from vibrations using piles as barriers[J].Journal of Engineering Mechanics,1988.114(11):1854-1870.
[13]徐斌,雷晓燕,徐满清,等.饱和土体中空沟对移动荷载被动隔振的2.5 D边界元法分析[J].岩土力学,2012(4):1079-1086+1102.
[14]袁万,蔡袁强,史吏,等.基于2.5维有限元饱和土地基中空沟隔振性能研究[J].岩土力学,2013(7):2111-2118.
[15]朱兵见,熊浩.二维饱和地基中空沟主动隔振分析[J].岩土力学,2013(2):462-467.
Vibration IsolationAnalysis of Elastic Continuous Barrels in Saturated Soil
DING Hai-bin1,YANG Yuan-ye1,XU Chang-jie1,2,TONG Li-hong1,ZHAO Xiu-shao1
(1.Jiangxi Key Laboratory of Infrastructure Safety Control in Geotechnical Engineering,East China Jiaotong University,Nanchang 330013,China;2.Research Center of Coastal and Urban Geotechnical Engineering,Zhejiang University,Hangzhou 310058,China;)
Based on Biot wave theory,the reflection coefficients of P1wave,P2wave and S wave and the transmission coefficients of P wave and S wave generated by S wave incidence to a linearly elastic barrier in saturated soil are derived in an analytical form.A numerical example is given.The relationship among the above-mentioned coefficients and the density,Poisson’s ratio and elastic modulus of the barrier are analyzed.The results demonstrate that the density of the barrier has little influence on the reflection coefficients of P1and P2waves.However,with the increase of the density of the barrier,the reflection and transmission coefficients of S wave and the transmission coefficient of P wave are gradually reduced and tend to stable finally.Variations of the Poisson’s ratio and the elastic modulus of the barrier have little effect on the reflection coefficients of P1and P2waves and the transmission coefficient of P wave,while it has great influence on the reflection coefficient and transmission coefficient of S wave.The reflection coefficient of S wave increases with the increase of Poisson’s ratio and elastic modulus of the barrier.The transmission coefficient of S wave decreases with the increase of Poisson’s ratio of the barrier,while increases with the increase of the elastic modulus of the barrier.
vibration and wave;S waves;saturated soil;vibration isolation barrier;reflection coefficient;transmission coefficient
TU435
A
10.3969/j.issn.1006-1355.2017.05.031
1006-1355(2017)05-0149-05
2017-03-10
江西省岩土工程基础设施安全与控制重点实验室资助项目(20161BCD40010);国家重点基础研究发展计划资助项目(973计划)(2015CB057801);国家自然科学基金资助项目(51338009,51668018)
丁海滨(1991-),男,硕士研究生,主要从事饱和土中波传播研究。
E-mail:616408201@qq.com
