部分观测下结构质量识别迭代及滞回力识别方法
2017-10-23王云,许斌
王 云,许 斌
(1.湖南大学 土木工程学院,长沙 410082; 2.华侨大学 土木工程学院,福建 厦门 361021;3.华侨大学 福建省结构工程与防灾重点实验室,福建 厦门 361021)
部分观测下结构质量识别迭代及滞回力识别方法
王 云1,许 斌2,3
(1.湖南大学 土木工程学院,长沙 410082; 2.华侨大学 土木工程学院,福建 厦门 361021;3.华侨大学 福建省结构工程与防灾重点实验室,福建 厦门 361021)
在强动力荷载作用下结构滞回力可直接描述损伤的发生发展过程,并用于结构耗能的定量评估。提出一种仅利用结构部分自由度上加速度响应时程且结构刚度、阻尼、质量均未知时的结构质量识别迭代和滞回力识别方法。首先基于质量预估值利用扩展卡尔曼滤波方法预测结构的位移和速度响应以及未知加速度响应,利用二重切比雪夫多项式对质量进行更新并迭代直到收敛,最后基于收敛的质量识别值描述结构滞回性能,识别结构滞回力。在一个多自由度集中质量数值模型中引入磁流变阻尼器模拟非线性构件,在结构仅已知部分自由度上加速度响应时程的条件下,数值模拟结果发现结构质量分布和阻尼器的滞回阻尼力均有良好的识别结果,同时考察了测量噪声的影响。
振动与波:非线性恢复力识别;质量识别;扩展卡尔曼滤波;切比雪夫多项式模型;部分加速度测量
基于结构动力响应测量和结构动力学基本原理对结构物理参数进行识别,借此描述结构状态和损伤,并对结构进行补强和加固进而提升结构的使用性能是土木工程领域紧迫的课题之一。
相对于非线性动力系统而言,对线性系统进行参数化识别开展得较早,研究比较深入[1–3]。然而,结构在地震等强动力荷载作用下的损伤发生发展以及破坏过程会呈现出典型的非线性特征。因此,研究适用于非线性动力系统的结构识别方法具有重要意义。李宏男等对在结构健康监测和损伤识别中研究非线性系统的识别问题的重要性进行了阐述[4–5]。Smyth等提出带遗忘因子的修正最小二乘法来识别描述非线性滞回性能的Bouc-Wen模型中参数的识别,并通过在链式多自由度结构中引入Bouc-Wen非线性构件验证了方法的可行性[6]。此外实际土木工程结构由于材料和结构形式的差别其非线性行为差异明显,难以用准确的非线性数学模型建立。国外学者在结构免模型识别上也得到了长足的发展。在免模型的结构非线性状态识别方面,Masri和Caughey最早提出了恢复力曲面法(Restoring Force Surface Method),并利用该方法对单自由度非线性结构的非线性恢复力进行了有效识别[7]。之后该方法被推广到多自由度系统,识别多自由度系统的非线性恢复力,即滞回性能[8]。Xu等利用已知激励和结构响应,基于等价线性理论和最小二乘法对结构非线性恢复力进行识别,并通过装有磁流变阻尼器的四层剪切型框架结构模型的动力试验测量数据,验证了该方法的有效性,并考虑激励部分未知时的实现方法[9–12]。许斌等利用数值模拟和试验实测数据验证了基于幂级数多项式和切比雪夫多项式模型的含磁流变阻尼器的非线性多自由度系统滞回力识别方法的有效性[13]。
本文提出基于扩展卡尔曼滤波(Extended Kalman Filter,EKF)和切比雪夫多项式模型,在结构仅部分自由度受激励且仅部分自由度上加速度响应已知时的质量分布迭代识别和多自由度结构滞回力识别方法。通过在一个多自由度线性系统中引入非线性构件磁流变阻尼器,形成一个非线性结构,且非线性结构的非线性特征具有合适的数学物理模型来描述时,通过数值模拟验证所提出的方法识别质量分布和结构滞回力的有效性,并考虑测量噪声的影响。
1 非线性系统的扩展卡尔曼滤波算法
为运用结构部分加速度响应测量进行非线性系统的滞回性能识别,利用EKF算法预测结构各个自由度位移和速度响应以及未知加速度响应,并识别非线性系统的物理参数。
对于一般的n自由度非线性动力系统,其运动方程可写为

其中M为质量矩阵,K为刚度矩阵,C为阻尼矩阵,fnon(θ)为非线性恢复力向量分别为结构加速度、速度、位移向量,f(t)为外激励向量。
定义以下扩展状态向量

X(t)表示t时刻的状态向量,、和分别为待识别的阻尼、刚度和非线性系统参数向量,不考虑参数的时变。于是得到如下的扩展状态方程

式(3)改写成如下形式

当观测部分加速度响应时,对于离散采样点,时刻tk=k t时的观测响应可以写为如下形式

其中△t为采样时间间隔,y(k)为tk时刻的观测向量,V(k)为均值为零的观测噪声向量,满足以下两式要求

其中R为观测噪声的协方差矩阵,δij是Kronecker算子。
EKF算法通过在滤波估计值附近作线性化处理,逐步获得下一时刻的最优估计,其主要计算步骤如下。
1)状态预测

2)误差协方差预测方程

其中

3)增益矩阵

其中

4)状态滤波方程

5)误差协方差方程

在假定结构质量和已知部分结构加速度的情况下,运用EKF,可以识别出非线性结构的状态向量以及参数向量,包括结构位移、速度和位置加速度,以及结构线性和非线性恢复力的模型参数。
以下通过引入二重切比雪夫多项式对结构的质量进行识别与更新,并对多自由度结构的滞回性能进行描述。
2 基于二重切比雪夫多项式的多自由度结构滞回力识别方法
2.1 二重切比雪夫多项式
余弦函数的多倍角公式如式(15)所示。

令θ=arccosα,则函数
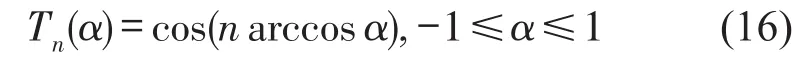
其中n=0,1,2,…
可得到如下递推关系

由式(17)递推得到第一类切比雪夫多项式,其前几阶可以表示为
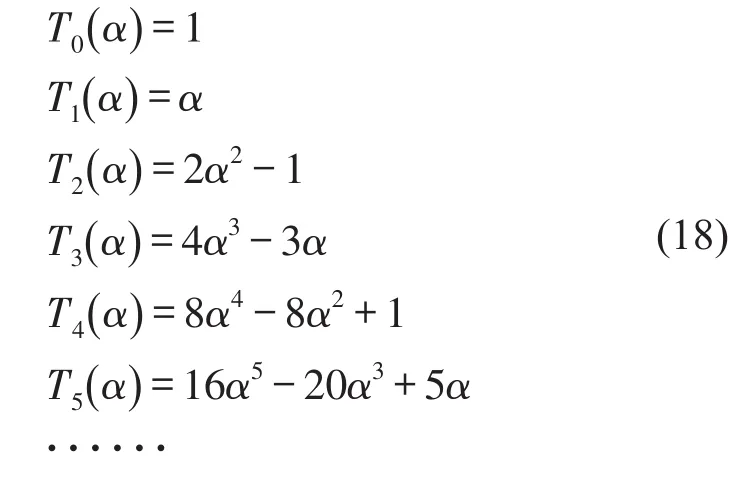
2.2 结构质量分布与滞回力的识别
将(1)式的运动方程改写为下式
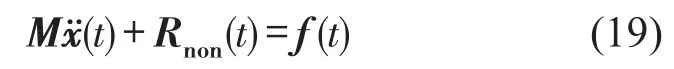
其中Rnon(t)为结构总非线性恢复力,由线性系统的弹性恢复力、粘性阻尼力以及非线性构件提供的非线性恢复力构成,一般可用结构相对速度和位移响应来表示,如式(20)所示

式中x˙(t),x(t)分别为结构相对速度和位移响应。
由于切比雪夫多项式的正交性,在非线性链式多自由度集中质量模型中,两集中质量间的滞回力可近似表示为下式。
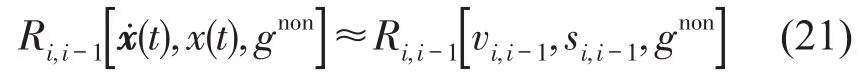
由于切比雪夫多项式中自变量的定义域为[-1,1],需将相对位移和相对速度进行标准化处理,v′i,i-1和S′i,i-1是经过标准化层间相对速度和相对位移,通过下式确定。
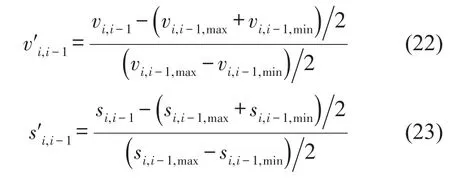
于是,滞回力可用二维切比雪夫多项式模型来表示
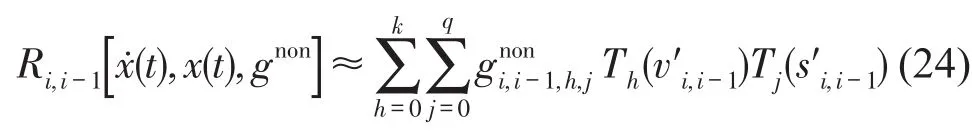
考虑一般情况,即结构仅有部分自由度上作用有激励力。在这种非完整激励条件下,以一个3自由度体系为例,假设外激励仅作用在第3个自由度上,则各自由度的运动平衡方程可表示为式(25)-式(27)。

由式(25)可得
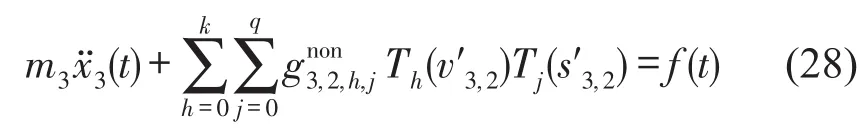
运用已知部分加速度响应以及以上通过EKF预测的结构位移、速度和加速度响应,可以利用最小二乘优化求解得到结构的质量以及滞回力切比雪夫多项式的参数。进而根据牛顿第三定律可对其他自由度上质量和滞回力进行识别。
如根据自由度2与3之间的相互作用力的互等关系

由式(26)和式(29)得

同理识别出自由度2上的质量以及自由度2与1之间的滞回力。同理,可得自由度1与地面之间的滞回力以及自由度1的质量。于是得到结构各自由度间的滞回力以及各质点质量识别结果。
3 基于EKF和二重切比雪夫多项式的质量以及滞回力识别迭代算法
综合运用EKF和二重切比雪夫多项式,通过迭代算法,可进行结构质量和滞回力的识别。该迭代算法的框图如图1所示。
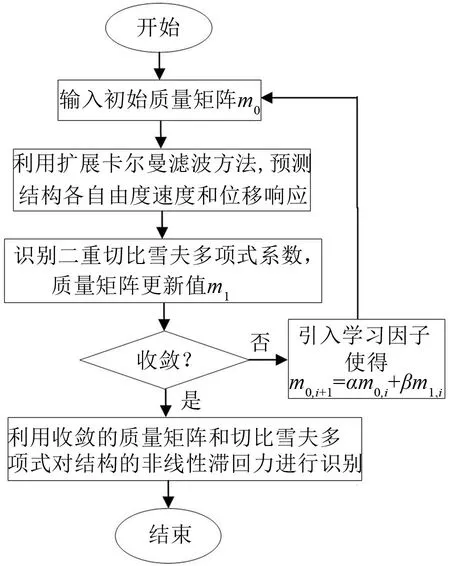
图1 滞回力和质量识别迭代算法流程
首先,将初始结构质量的预估值代入到EKF中预测出结构位移和速度以及未知加速度响应;其次,利用结构位移和速度响应,基于二重切比雪夫多项式,得到结构的质量的更新值;最后,引入学习因子,对结构质量近似值进行修正,进行迭代求解。在本算法中,学习因子α和β均为0.5。
4 数值算例
4.1 计算模型与参数
以一个具有4个集中质量的结构体系为例,为模拟结构的非线性行为,在结构第四层安装一个非线性构件磁流变阻尼器MR。线性结构各层参数取值如下:质量mi=200 kg,阻尼ci=100 N·s/m,刚度ki=3×104N/m ,(i=1,2,3,4)。不失一般性,假设外激励仅水平方向作用在结构的第3个自由度上,其他集中质点上不施加荷载。
在数值模拟中MR阻尼器采用修正的Dahl模型[15]。其表达式为

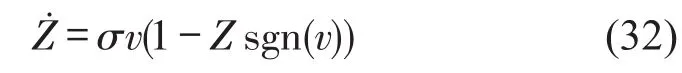
式中参数σ用来控制阻尼器恢复力滞回曲线的形状。在本文中,σ=50 s/m,K0=50 N/mC0=199 5 N·s/m,Fd=34.85 N,f0=0 N。
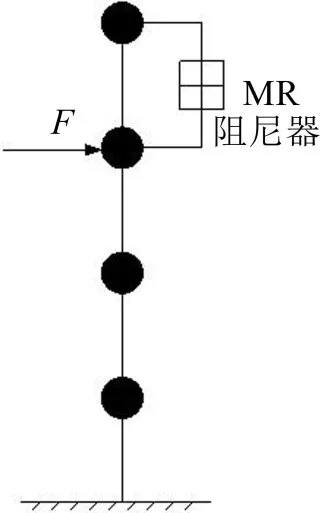
图2 非线性结构计算模型
针对本问题,EKF的扩展状态向量为
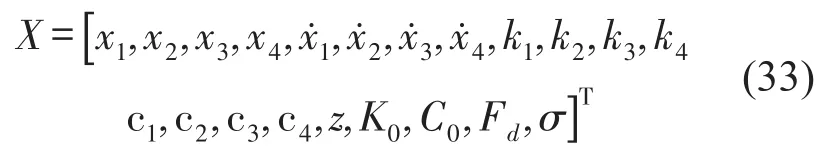
为了更好地模拟结构非线性恢复力,本文采用的切比雪夫多项式模型中取k+q=3。观测第1、第3、第4集中质点上的加速度响应作为已知加速度响应,第2质点上的加速度响应未知。另外,作用在第3质点上的外激励已知。
本文选用的外激励采用随机激励,其时域图如图3所示。
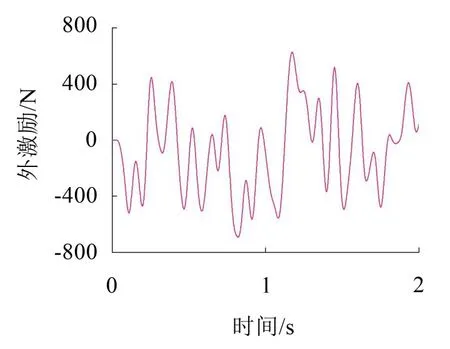
图3 结构随机外激励荷载时程
荷载作用时间为2 s。结构在该动力荷载作用下的响应采用4阶龙格库塔(Runge-Kutta)积分法计算,积分步长为0.000 5 s。其中,加速度混入了5%的量测噪声,以考察该方法的抗噪性能。此外,为了验证算法在不同初始条件下的收敛性能,本文分别考虑了初始质量为理论值110%和90%两种情况。
4.2 工况一:质量大于真实值10%
(1)质量、参数与响应识别效果
基于扩展卡尔曼滤波和切比雪夫多项式,识别出质量的真实值收敛曲线如图4所示。收敛准则为后一次迭代与前一次的差的绝对值不大于0.1 kg。四个自由度对应的质量识别结果分别为m1=197 kg,m2=199 kg,m3=200 kg,m4=198 kg。与真实值吻合较好,本文方法可有效识别出结构质量分布。在迭代结束时,根据结构第1、第3、第4集中质点的加速度响应观测值,基于EKF,预测出结构所有质点的位移和速度响应,并与积分计算所得结果进行对比,结果如图5和图6所示。
对于未知的第2层加速度响应,在得到速度预测值的情况下根据线加速度法的原理,可计算出第2层加速度响应。第2层加速度响应预测值与真实值的比较如图7所示。
迭代结束时,结构刚度、阻尼以及MR阻尼器的各参数的识别结果与真实值的比较见表1。比较发现,刚度与阻尼以及MR阻尼器的参数均有比较好的识别效果。
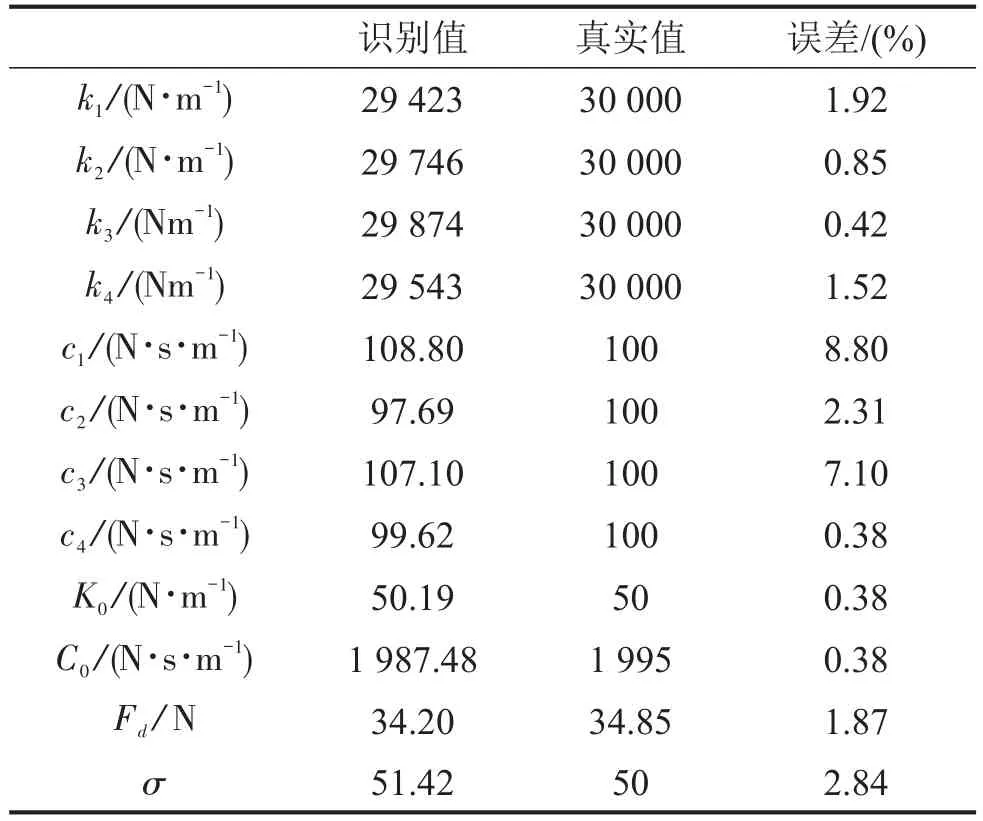
表1 结构参数识别结果

图4 质量识别结果迭代过程

图5 结构位移响应识别结果
(2)滞回力识别结构
通过EKF方法识别的非线性参数和所有质点的位移和速度响应,MR阻尼器的非线性恢复力的识别值与真实值比较如图8所示,对比发现,识别出的非线性恢复力有良好的识别精度。

图6 结构速度响应识别结果

图7 第2层加速度响应识别值

图8 MR阻尼器恢复力识别结果
工况二考虑了在质量初始值小于理论值10%的情况。同样在观测的结构加速度响应中添加了5%的噪声,仍采取图3所示的随机激励,所得识别效果如下。
4.3 工况二:质量小于真实值10%
(1)质量、参数和响应识别结果
基于EKF和二重切比雪夫多项式识别出的质量为m1=202 kg,m2=200 kg,m3=200 kg,m4=202 kg,与真实值吻合较好,说明本文提供的方法在质量初始值小于真实值10%的情况下可以有效识别出结构的质量分布,验证了该方法的有效性,其质量识别结果收敛曲线如图9所示。

图9 质量识别迭代过程
迭代结束时通过扩展卡尔曼滤波识别的参数结果如表2,识别出的参数与真实值吻合较好,在质量小于10%的工况下,结构的刚度、阻尼以及非线性参数均有良好的识别效果。
(2)滞回力识别结果
识别出的MR阻尼器滞回力结果如图10所示。在质量初始值低于真实值10%的情况下,MR阻尼器滞回力识别值与真实值吻合较好。

表2 结构参数识别结果

图10 MR阻尼器恢复力识别结果
5 结语
本文提出了一种在非完整激励下仅利用结构部分自由度上加速度响应时程,在结构质量、刚度和阻尼信息未知时,基于EKF和二重切比雪夫多项式模型的质量分布迭代识别以及结构滞回力识别方法。
通过在一个4自由度线性模型中引入磁流变阻尼器作为非线性构件,形成非线性结构,运用其在一个集中动力荷载作用下3自由度上加速度响应时程,未知结构质量分布,对结构中质量分布以及MR的滞回力进行识别。考虑加速度测量噪声以及不同质量初始值下的计算结果。数值模拟结果表明,仅利用作用在部分自由度上的外激励及其部分加速度响应信息,所提出的算法在加速度测量噪声以及不同质量初始值下均可对结构的质量分布以及滞回力进行识别,该算法具有较好的抗噪声能力。
结构滞回力的识别结果可以直接描述结构构件在强动力荷载作用下的非线性行为的发生发展过程,而且可以用于定量计算结构构件的耗能,对工程结构在地震、爆炸等强动力荷载作用下的性能评估具有重要意义。所提出的方法可以运用于质量未知情况下非线性系统的识别问题。
[1]WU Z S,XU B,HARADA T.Review on structural health monitoring forinfrastructure[J].Journalof Applied Mechanics,2003,70(6):1043-1054.
[2]孙鸿敏,李宏男.土木工程结构健康监测研究进展[J].防灾减灾工程学报,2003,23(3):92-98.
[3]宗周红,任伟新,阮毅.土木工程结构损伤诊断研究进展[J].土木工程学报,2003,36(5):105-110.
[4]李宏男,高东伟,伊延华.土木工程结构健康监测系统的研究状况与进展[J].力学进展,2008,38(2):151-166.
[5]李宏男,李东升.土木工程结构安全性评估、健康监测及诊断评述[J].地震工程与工程振动,2002,22(3):82-90.
[6]A W SMYTH.On-line parametric identification of MDOF nonlinear hysteretic systems[J].Journal of Engineering Mechanics,1999,125(2):133-142.
[7]MASRISF,CAUGHEYTK.Anonparametric identification technique for nonlinear dynamic problem[J].Journal ofApplied Mechanics,1979,46(3):433-447.
[8]MASRI S F,SASSI H,CAUGHEY T K.Nonparametric identification of nearly arbitrary nonlinear systems[J].Journal ofApplied Mechanics,1982,49(5):619-628
[9]XU B,HE J,MASRI S F.Time domain data-based model free structural nonlinear performance identification[C].Proceeding of International Symposium on Innovation&Sustainability of Structures in Civil Engineering,2009:59-69.
[10]XU B,MASRI S F.Nonlinearity identification for a frame modelstructure with MR dampers underlimited excitations[J].Asia-pacific Young Researchers&Graduates Symposium,2010,159:167.
[11]XU B,HE J,AND MASRI S F.Data-based model-free hysteretic restoring force and mass identification for dynamic systems[J].Computer-Aided Civiland Infrastructural Engineering,30:2-18,2015
[12]XU B,HE J,MASRI S F.Data-based identification of nonlinearrestoring forceunderspatially incomplete excitationswith powerseriespolynomialmodel[J].Nonlinear Dynamics,2011,67(3):2063-2080.
[13]许斌,辛璐璐,贺佳.基于二重切比雪夫多项式的多自由度系统SMA非线性恢复力识别[J].振动与冲击,2014,33(16):6-13.
[14]周强,瞿伟廉.磁流变阻尼器的两种力学模型和试验验证[J].地震工程与工程振动,2002,22(4):144-150.
Mass and Hysteretic Force Identification for Structures Based on Limited Measurement Data
WANG Yun1,XU Bin2,3
(1.College of Civil Engineering,Hunan University,Changsha 410082,China;2.College of Civil Engineering,Huaqiao University,Xiamen 361021,Fujian China;3.Key Laboratory for Structural Engineering and Disaster Prevention of Fujian Province,Huaqiao University,Xiamen 361021,Fujian China)
Structural hysteretic force can provide a direct description for the initiation and development of structural damage and can be used for the quantitative structural energy consumption evaluation under dynamic loadings.In this study,a mass distribution and iterative structural hysteretic force identification approach is proposed.Acceleration responses at part of the degrees of freedoms(DOFs)of a nonlinear structure with unknown structure mass,stiffness and damping coefficients are employed for the hysteretic force and mass identification.First of all,the extended Kalman filter(EKF)is employed to forecast structure displacement,velocity in all DOFs and the unmeasured acceleration responses with the assessed mass matrix and the partially measured acceleration response.Then,a double Chebyshev polynomial model is employed to identify the hysteretic force and to update the mass.With the updated mass,the identification approach is repeated until the convergence criterion is met.Finally,a multi-degree-of-freedom(MDOF)structure equipped with a magnetorheological(MR)damper is employed to simulate the non-linear components.Based on the approach,the hysteretic force and mass distribution are identified successfully with partially known noise-polluted acceleration measurements.
vibration and wave;nonlinear restoring force identification;mass identification;extended Kalman filter;Chebyshev polynomial model;partial acceleration measurement
TH212;TH213.3 文献标示码:A
10.3969/j.issn.1006-1355.2017.05.030
1006-1355(2017)05-0142-07
2017-03-14
国家自然科学基金资助项目(50978092)
王云(1992-),男,安徽省舒城县人,硕士生,主要研究方向为非线性恢复力识别。
E-mail:wangdasi4144@qq.com
许斌(1972-),男,博士,教授,博士生导师。
E-mail:binxu@hqu.edu.cn
