非圆行星齿轮马达轮系特殊结构的设计
2017-10-23王帅帅李殿起汪鹏飞张少华
王帅帅,李殿起,汪鹏飞,张少华,魏 爽
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
·设计计算·
非圆行星齿轮马达轮系特殊结构的设计
王帅帅,李殿起,汪鹏飞,张少华,魏 爽
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
提出了一种高阶非圆行星齿轮马达,相比于波兰SOK马达,高阶非圆齿轮马达径向力平衡,排量大,脉动小,性能更优。如何确定齿轮副中各非圆齿轮的节曲线和齿廓是设计非圆齿轮的关键。本文首先依据非圆齿轮的啮合原理,得出封闭节曲线的方程式,确定在节曲线上均匀分布的轮齿的位置,并通过利用产形齿轮与非圆柱齿轮啮合关系来确定非圆柱齿轮的齿廓。通过MATLAB编程软件对相关参数方程进行相应的计算,快速的计算出准确的非圆齿轮副的节曲线和齿廓。最后用实例验证了该方法的可行性。
非圆行星齿轮马达;马达性能;参数方程;MATLAB
0 前言
非圆行星齿轮马达是一种新型低速大扭矩马达,其主要特点包括低速运转平稳、启动效率高、转动惯量小、加速和制动时间短、结构紧凑、布置灵活等。变中心距的非圆行星齿轮副是非圆齿轮马达的关键构件。该齿轮副由非圆太阳轮、非圆内齿圈和圆柱行星齿轮构成。本文将非圆齿轮马达按照非圆行星齿轮副的结构命名。所谓6-8(4-6)型行星马达,是指太阳轮节曲线的周期数n1=6(4),内齿圈节曲线的周期数n3=8(6)。对于不同非圆太阳轮节曲线方程从而得到的马达性能显然也是不同的。在非圆太阳轮运转一周的过程中,共有n1n3/(n1+n3)个吸液、排液的过程,n1、n3越大,马达单位体积排量越大,脉动率越小。因此高阶非圆齿轮马达相比于应用中的SOK马达,具有更深刻的研究价值。本文以太阳轮的节曲线是高阶椭圆,内齿圈的节曲线是周期曲线为研究对象。不仅要确定椭圆齿轮副中太阳轮和内齿圈的齿数z1、z3,行星轮的齿数z2,还要计算出椭圆的中径Rz和偏心率e。目前存在的文献中只给出了3-4及4-6型齿轮马达的上述参数,更高阶椭圆齿轮机构无参考资料。为此,本文从已知参数n1、n3出发,结合非圆齿轮的特点,用MATLAB语言求解出所需参数,得到节曲线方程和齿廓的方程。从而得到完整而精确的高阶非圆行星齿轮机构。
1 参数求解

此马达中的齿轮副的节曲线应该符合以下的要求:
(1)齿轮副要做连续的转动,来保证周期性的运动关系,因此太阳轮与内齿圈的节曲线都必须是封闭的。
高阶椭圆太阳轮的极坐标方程为
(1)
式中,Rz是中径;e是偏心率;A是椭圆的长轴长度;μ1是向径r与啮合点切线的正方向的夹角。内齿圈的节曲线r3的方程为
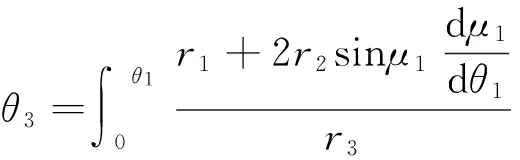
(2)
在φ1=0-2π范围内,r1变化n1个周期,n1阶椭圆的节曲线是闭合的。以n1阶太阳轮来计算非圆轮系中内齿圈的节曲线的时候,为了使内齿圈的节曲线封闭,必须满足条件:
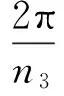
(3)
(2)太阳轮和内齿圈的轮齿均匀分布在各自的节曲线上。
太阳轮(内齿圈)轮齿均布的条件是太阳轮(内齿圈)旋转2π角度得到的节曲线长度等于πmz1(πmz3)。由以上方程,给出太阳轮和内齿圈的阶数n1、n3,行星轮的齿数z2,合适的模数m后,借助MATLAB语言将两个条件作为约束函数就能得到参数Rz、e。其中,偏心率e的值与模数、齿数无关,对于相同的太阳轮曲边数,内齿圈的曲边数与太阳轮的曲边数差值既n3-n1的值加大时,偏心率应减小。
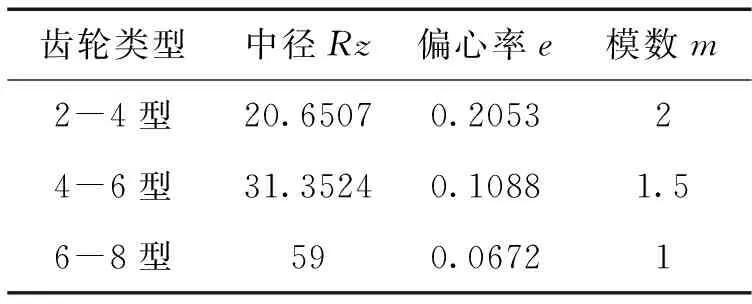
表1 太阳轮的节曲线是高阶椭圆时部分参数的搭配
2 非圆齿轮的齿廓及节曲线的确定
2.1 节曲线的形成
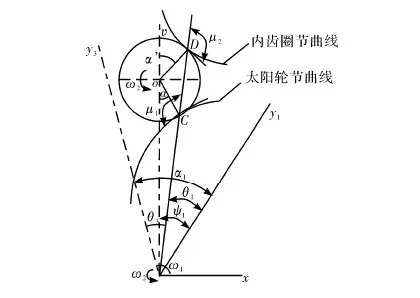
图1 行星轮系的运动图
根据已知太阳轮的节曲线来求出内齿圈的节曲线:
太阳轮所在固定坐标系为o1x1y1、o3x3y3是随同内齿圈回转的动坐标系。行星轮2的节圆与太阳轮的节曲线在C点接触,与内齿圈的节曲线在D点接触。由三心定理,C、D、o1在同一条直线上。对于动坐标系o3x3y3来说,内齿圈满足的极坐标方程是
(4)
输入不同的参数Rz、e,太阳轮的阶数n1、内齿圈的阶数n3,行星轮的半径r2。通过MATLAB语言分析,就能得到不同非圆行星齿轮副的节曲线。图2、图3是分别以4-6和6-8齿轮为算例,得到的节曲线图形。
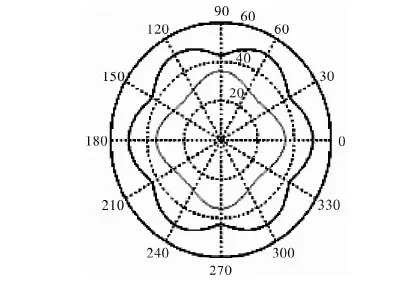
图2 4-6阶非圆行星齿轮副节曲线
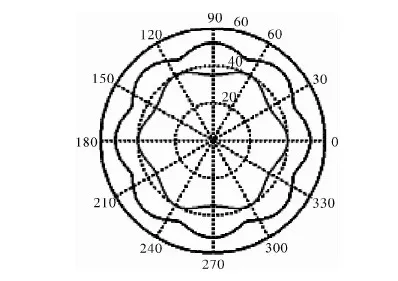
图3 6-8阶非圆行星齿轮副节曲线
以6-8阶椭圆齿轮副作为算例,图4~6分别绘制了太阳轮的极径,内齿圈的转角、内齿圈角速度与太阳轮转角的对应关系。
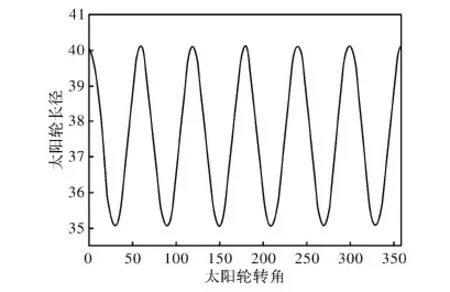
图4 太阳轮的极径与太阳轮的转角之间的关系图
通过图4~6可以看出在太阳轮旋转一周的过程中,太阳轮的极径以自身阶数为周期变化,内齿圈的转角与太阳轮的转角关系成立。并且能找出内齿圈的角速度在一个曲线段内变化规律,为齿轮动力学研究提供了方向。同时也验证了通用程序的可行性。
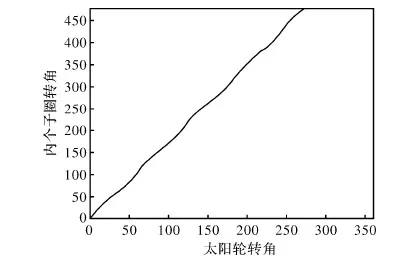
图5 转角与太阳轮转角之间的关系图
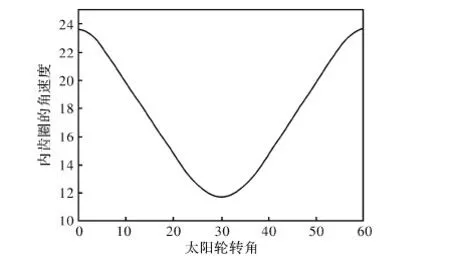
图6 角速度与太阳轮转角之间的关系图
2.2 齿廓的形成
节曲线形状导致不同的非圆齿轮的齿廓一般也是各不相同的,对于这种节曲线有内凹特点的非圆齿轮,需要用非圆齿轮和产形齿轮内外啮合来设计这种非圆齿轮的齿廓。
如图7所示,产形齿轮和非圆太阳轮呈外啮合状态,产形齿轮的节圆在太阳轮的节曲线上作逆时针方向的滚动。滚过一定角度后,两齿轮的节圆在D点接触。
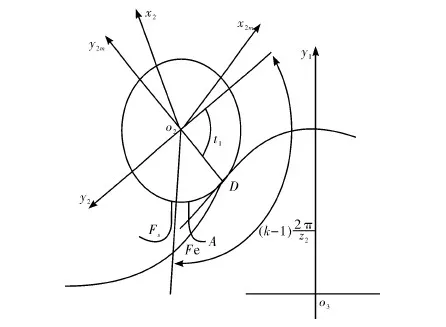
图7 非圆太阳轮齿廓的形成
坐标系o1x1y1是静坐标系,坐标系o2x2y2是与产形齿轮副连的的动坐标系。根据求解产形齿轮顺时针齿廓的方法。对于顺时针齿廓的任意一点Fs,此处对于点的半径rs为
(5)

ts=α-αs
(6)

在坐标系o2x2my2m中,Fs的坐标用x2sm和y2sm表示。则在静坐标系o1x1y1中,Fs点的坐标为
(7)
Fs点的坐标是关于t1的参数方程。当t1由小变大时,啮合点在太阳轮的齿廓上由齿顶部运动到齿根。另一侧齿廓可以采用同样方法得到。
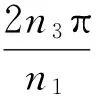
(8)
当非圆行星齿轮应用在液压马达上时,可以将节曲线的法向等距线作为太阳轮和内齿圈的齿顶线、齿根线。
3 校检参数
为保证得到的非圆齿轮副的正确性以及在液压马达中的实用性,需要从非圆齿轮的重合度和轮齿在节曲线上的位置两方面进行验证。
3.1 校检重合度
齿根过渡曲线是轮齿干涉分析的基础,也是求解齿根应力集中系数,进行弯曲强度校核的基础。对于节曲线是高阶椭圆的非圆齿轮,因为将节曲线的法向等距线作为齿顶线和齿根线时存在一定的误差,所以需要做重合度校验。非圆齿轮的重合度的公式为
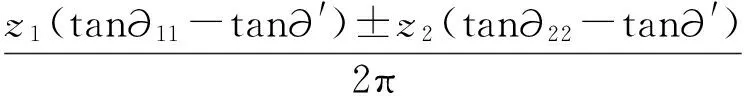
(9)
其中,外啮合时重合度是正值,内啮合时重合度是负值。其中,∂′是啮合角,∂11、∂22是两齿轮齿顶圆压力角。通过程序算出6-8行星轮和太阳轮啮合的重合度最小值是1.4888,并且满足要求。
3.2 校检齿轮位置
非圆齿轮上的主、从动轮的节曲线上切点的位置是一一对应的,因此,非圆齿轮的轮齿在节曲线上的位置也是固定不变的。所以有必要判断MATLAB画出的齿廓在节曲线上是不是均匀分布的。图8就是利用MATLAB语言得出的节曲线等分点。
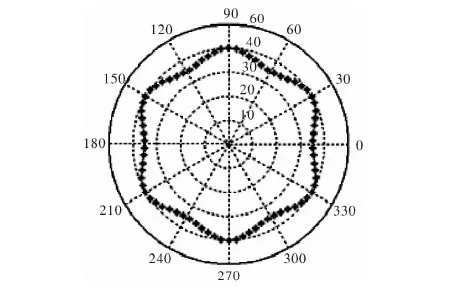
图8 节曲线的等分点
最后,把得到的节曲线和齿廓数据点导入到SOLIDWORKS进行实体拉伸就能得到图9所示的高阶非圆齿轮副的三维模型。
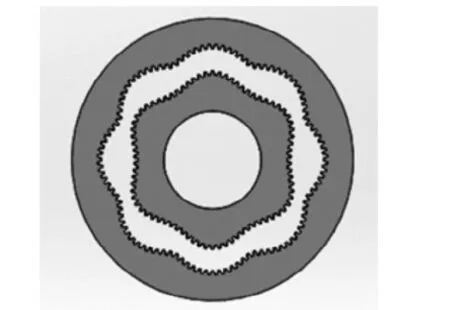
图9 高阶非圆齿轮副的三维模型
4 结论
以非圆齿轮的节曲线和齿廓需满足的条件为边界条件,确定出了非圆行星齿轮的中径、偏心率以及节圆方程和齿廓数据。解决了非圆齿轮参数难以计算的问题。
提出了排量大,径向力小,振动小的6-8阶非圆行星齿轮马达,突破了以往研究的界限,为高阶非圆行星齿轮马达的发展及应用提供了技术支持。
[1] 许健,许鸿昊. 4-6阶非圆行星齿轮系齿数确定的方法[J]. 煤炭学报,2007(03):23-26.
[2] 廖旋,姚文席.MATLAB在非圆行星齿轮节曲线设计中的应用[J]. 设计与计算,2006(12):107.
[3] 李建生,李华敏.不同类型非圆行星齿轮液压马达的性能分析[J]. 机械传动,1993,17(02):1-3.
[4] 王淑杰. 非圆齿轮传动的快速优化设计[D].合肥工业大学,2005.
[5] 熊镇芹. 非圆行星齿轮液压马达参数设计[J]. 机床与液压,2004(05):10-12.
[6] 杨善国,李磊,杜长龙. 非圆行星齿轮液压马达的发展及在煤矿机械中的应用展望[J]. 液压与气动,2007,(09):16-18.
[7] 刘生林. 非圆行星传动研究[J]. 机械设计, 1995(08):13-14.
[8] 许鸿昊,沈冰妹. 基于双圆弧节曲线的非圆行星齿轮机构[J]. 煤炭学报,2010,35(04):691-695.
[9] 何贵平. 内啮合非圆齿轮加工的数学模型及图形仿真[J]. 机械设计与研究, 2006,22(04):4-7.
[10] 王昱潭. 新型球面圆弧锥齿轮啮合原理的研究[J]. 煤矿机械,2011,32(09):10-13.
Design of non-circular planetary gear motor gear with special structure
WANG Shuai-shuai,LI Dian-qi,WANG Peng-fei,ZHANG Shao-hua,WEI Shuang
(Department of Mechanical Engineering,Shenyang University of Technology,Shenyang 110870,China)
A high order non-circular planetary gear motors are proposed in this article. High order non-circular planetary gear motor proves balanced radial force, great motor displacement, small pulsation, which is superior to SOK motor. The key of the gear design is to determine the pitch curve and tooth profile of each non-circular gear. First, based on engagement principle, the pitch curve equation and even-distributed tooth position are obtained. Then, using the engagement gear with non-circular gear in gear forming process, the tooth profile of non-circular can be obtained. The parametric equations of the gear pitch curve and tooth profile are obtained quickly and accurately by MATLAB. Finally, and the feasibility of the method is verified by the actual model.
non-circular planetary gear motor;motor performance;parametric equation
TH132.4
A
1001-196X(2017)05-0059-05
2017-01-06;
2017-03-17
国家自然科学基金(51105257,51310105025)及辽宁省高等学校杰出青年学者成长计划(LQJ2014012)
王帅帅(1993-),男,辽宁大连人,沈阳工业大学硕士研究生。
