“平行四边形面积”教学设计

文︳李 芳

“平行四边形面积”教学设计

文︳李 芳

学生已经认识了平行四边形，并会计算长方形的面积。这些都是本课学习的基础。而平行四边形面积公式推导的方法，可以直接用于后续三角形面积公式、梯形面积公式的推导。

基于以上认识，可将此课教学目标设定为：

1.学生理解并掌握平行四边形面积计算公式，并能初步运用公式计算平行四边形面积。

2.学生通过观察、拼等活动，感受平行四边形面积计算公式的推导过程，体会将平行四边形割补为长方形的方法。

目标的实现必须要有内容作载体，过程作支撑，方法作保证。也就是说，本节课教学的内容之一显然是平行四边形面积公式，之二是割补的意义与方法。过程就是如何引出平行四边形的面积公式，如何想到要用割补方法将平行四边形转化为长方形。将平行四边形割补为长方形的方式有多种，可选择学生容易接受的一种或两种转化方式讲解，其余的方式学生可在课后交流。

为此，可设计下面的教学过程。

一、提出问题

出示问题：请同学们仔细观察图中的长方形和平行四边形，它们的面积会不会相等呢？

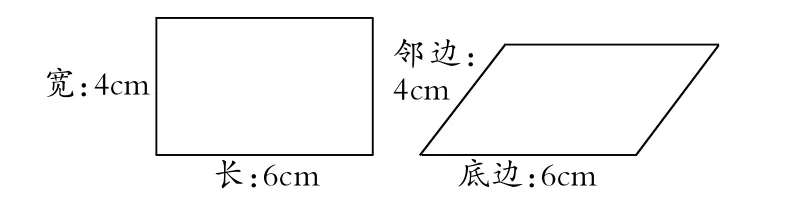
学生出现了相等与不等两种意见。如何解决？学生可独立思考，提出自己的解决方案。如都放到方格纸上数；将平行四边形剪成小长方形，然后贴到大长方形上去；还可以将平行四边形6cm的边与长方形6cm的边重合，将平行四边形拉成长方形……

二、剪剪拼拼

从学生求平行四边形面积的思路中发现，不论哪种方式都是将平行四边形变为长方形再求面积。这就启发我们：可以将平行四边形变为长方形。那么怎么样进行转化呢？这时可鼓励学生想办法剪拼，然后汇报方法。如通过剪拼左边多余的三角形，把平行四边形变成一个长方形（如图）。

图形变化了，高在哪？这里老师应引导学生观察图形变化前后的情况，发现平行四边形的高就是拼成长方形后长方形的宽。老师应引导学生对照前后图形仔细观察，哪条边变了，变成了什么；哪条边没有变；哪块图形变了，变成了什么；哪块图形没有变。不要小看这样的详细讲解，几何教学就必须这样落实，不能浮光掠影，否则，学生就不会看图，更不会解几何题。

学生可能还会有其他剪拼方法，老师可将这些方法展示在黑板上，课后大家再交流。课堂上，老师对所有的方法不要一一讲解，最多再选一种方法讲解。

三、总结公式

如何由长方形面积公式得到平行四边形面积公式？教师可引导学生观察图形变化前后的面积变化情况，从而得到：原来的平行四边形通过剪拼变为长方形后，面积不变。因此，可以利用长方形面积公式推导出平行四边形面积，即平行四边形面积=底×高，用字母表示为：S=a×h。

接下来，教师引导学生观察图形，并强调：从形式上看，平行四边形面积公式与长方形面积公式是相同的，只是字母表示的几何量不同。因此，运用公式时，如果找到了底边，就要找底边上对应的高。反之，找到了高，就要找高所对应的底边。不然就容易出错。

总结了平行四边形面积计算公式，接着要运用公式计算面积。可分下面几个层次设计练习题。

1.基本练习，算一算：教材第89页第1题。

2.变式练习，选一选（1）。

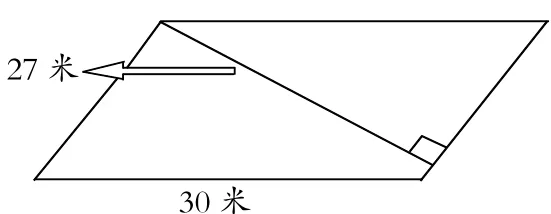
选择正确的算式计算平行四边形的面积（ ）。

①20×30=600（平方米）

②30×27=810（平方米）

③20×27=540（平方米）

3.变式练习，选一选（2）。

下面两个平行四边形的面积（ ）。

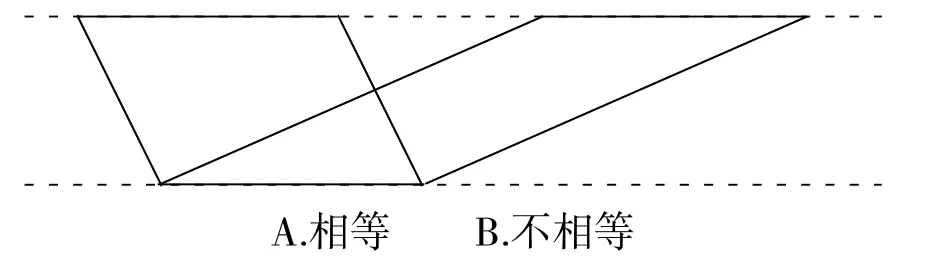
（作者单位：长沙市雨花区红星第二小学）