自适应非局部数据保真项和双边总变分的图像去噪模型

郭 黎，廖 宇，李 敏，袁海林，李 军

(1.湖北民族学院 信息工程学院，湖北 恩施 445000；2.University of Groningen, Faculty of Mathematics and Computer Science, Groningen the Netherlands, 9747AG)

(*通信作者电子邮箱411985846@qq.com)

自适应非局部数据保真项和双边总变分的图像去噪模型

郭 黎1,2，廖 宇1*，李 敏1，袁海林1，李 军1

(1.湖北民族学院 信息工程学院，湖北 恩施 445000；2.University of Groningen, Faculty of Mathematics and Computer Science, Groningen the Netherlands, 9747AG)

(*通信作者电子邮箱411985846@qq.com)

针对常见去噪方法容易造成特定区域过度平滑、奇异结构残余噪声以及产生阶梯效应和对比度损失等问题，提出一种自适应非局部数据保真项和双边总变分的图像去噪模型，建立了自适应非局部正则化能量泛函和相应的变分框架。首先，对噪声图像利用自适应权值的非局部均值求得数据拟合项；其次，引入双边总变分正则化项，利用正则化系数来适度平衡数据拟合项和正则化项的影响；最后，通过能量函数最小化对不同的噪声统计快速求得最优解，从而达到降低残余噪声并纠正过度平滑的目的。通过理论分析和针对模拟噪声图像与真实噪声图像的实验结果表明，所提出的图像去噪模型能够较好地处理具有不同统计特性的图像噪声,与自适应非局部均值滤波去噪相比，所提算法的峰值信噪比(PSNR)值最多可以得到0.6 dB的改善；与全变分正则化图像去噪算法比较，所提算法的主观视觉效果明显更好，在去噪的同时图像纹理和边缘等细节信息保护得更好，PSNR值最多可以提高10 dB，而多尺度结构相似性度(MS-SSIM)指标可以提升0.3。因此，所提出的图像去噪模型可以在理论上更好地探讨如何合理处理噪声和图像内容本身的高频细节信息，在视频和图像分辨率提升等领域也具有良好的实际应用价值。

自适应非局部均值；数据保真项；正则化函数；双边总变分；图像去噪

0 引言

图像在获取、传输和存储等过程中常常会受到噪声的干扰，极大地影响了人们从图像中获取有用信息。通常情况下，对图像进行边缘检测、图像分割等高层次处理之前，需要图像进行去噪等预处理操作。因此图像去噪成为图像处理领域的热点问题，而研究去噪模型又是图像去噪中的关键点。近几年来许多学者提出了有效的图像去噪算法，如张峥嵘等[1]提出了一种针对泊松噪声图像的非局部全变分(Total Variation, TV)去噪模型，该模型在Bayesian框架下构造非局部TV正则化项实现了良好的去噪效果；胡学刚等[2]利用分数阶微分特有的幅频特性优势，提出一种基于分数阶导数的图像去噪变分模型，很好地保留了图像的细节和纹理等弱信息；Buades等[3-4]提出了非局部平均的算法并将其用于图像和视频去噪，其性能要优于其他经典的去噪方法，可以消除传统邻域滤波器中出现的伪影，然而它会产生块抖动效应影响去噪图像的视觉质量；杨爱萍等[5]使用相关系数匹配准则和噪声原子裁剪方法的奇异值分解(Singular Value Decomposition, SVD)和非局部正则化项，在提高同质区域平滑性的同时，更多地保留纹理和边缘等细节特征；费选等[6]提出一种基于优化加权全变差的复合正则化压缩感知图像重建模型，在视觉效果和客观指标上都有明显提高；耿海等[7]等提出一种基于可变指数及L1保真项的图像去噪算法，可以明显减少非边界区域阶梯效应的产生，同时增强了模型修复图像破损部分的能力。但是上述图像去噪方法普遍存在对图像细节特征保护不够好，容易产生灰度跳跃现象和阶梯效应等问题。因此，本文试图利用非局部均值(Non-Local Means, NLM)的去阶梯效应特点和总变分泛函的能量局限性，提出一种自适应非局部数据拟合项和双边总变分的图像去噪模型，建立自适应非局部正则化能量泛函和相应的变分框架，不仅能解决滤波方法去噪不彻底的问题，也可以克服正则化方法中存在的过平滑现象和阶梯效应，达到良好的图像去噪效果。

1 图像降质模型及去噪方法

通过分析噪声与图像信号之间的关系，噪声图像的降质过程如式(1)所示，其中f(x,y)是一个退化函数h(x,y)和噪声n(x,y)同时作用在输入图像u(x,y)上而得到的降质图像。式(1)中的噪声n(x,y)按其幅度的统计特征又可以分为高斯噪声、脉冲噪声、椒盐噪声和泊松噪声等很多种。

f(x,y)=u(x,y)*h(x,y)+n(x,y)

(1)

1.1 非局部均值滤波

图像去噪的目的是将含噪图像f(x,y)恢复成干净的原始图像u(x,y)，也就是说在去除噪声过程中不能破坏图像的主要几何结构。常用的邻域滤波等方法都是基于对原始图像的规则性假设，因此造成与噪声相似主特征的边缘、纹理等图像的精细细节在去噪的同时被平滑掉了。目前最广泛使用的、效果最好的去噪方法之一就是非局部均值滤波[3]，它是基于图像具有自相似性或冗余性这一规则性假设，设f为含噪图像，定义在二维有界区域Ω∈R2上。令x∈Ω为图像中的某一像素，y为其邻域窗的邻域像素，非局部均值去噪算法可以表示为：

(2)

(3)

其中：C为归一化系数；标准差为a；h为滤波参数，用来控制平滑的程度；w(x,y)为权值函数，且

(4)

其中Ga是高斯核函数。式(2)表示非局部均值采用图像中所有像素点的加权平均来估计待处理像素点的灰度值，它用图像块代替单个像素点来描述中心像素点的结构特征，通过对比图像块灰度分布的相似性来计算式(3)中的相似性权值w。另外，参与加权平均的像素点不局限于待处理像素点的周围邻域，而是扩展到整幅图像空间。对于图像中某一像素点(x,y)，其权值由当前中心块和邻域块的相似性来决定，越相似则权值越大，反之越小，如式(4)所示。不同图像不同部分的特征有所不同，为了更好地适应图像，所定义相似窗口的大小和形状也不尽相同。通常采用固定大小的正方形邻域作为中心像素点的相似窗口。非局部均值滤波器很好地保持了图像的边缘等结构信息，相较于经典的邻域滤波和双边滤波等去噪算法，得到了更良好的去噪效果。

1.2 基于变分的正则化

图像去噪是一个典型的不适定病态反问题，可以采用第一类Fredholm积分方法对病态反问题进行解析式分析或直接用最小二乘的方法求解，但仍然不能解决该问题的病态性，输入数据的微小扰动都会对解造成极大范围的波动。图像去噪本身就具有病态性，加上噪声对观测数据的影响，实际求得的解往往偏离真实解很远。为了解决问题的病态性，需要在解上尽可能多地添加有关真实解的特征信息，用这些特征信息来约束求解过程，从而找到最接近原真实解的最优解。最常用的解决方法是在目标函数后面附加一个正则化项，将真实解的先验信息约束引入其中，从而得到稳定的反问题的解[8-10]。基于正则化的图像去噪模型的基本形式为：

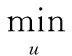
(5)

γTV(u)=‖▽u‖

(6)

其中▽是梯度算子，其应用在一维信号去噪的过程如图1[13]所示。

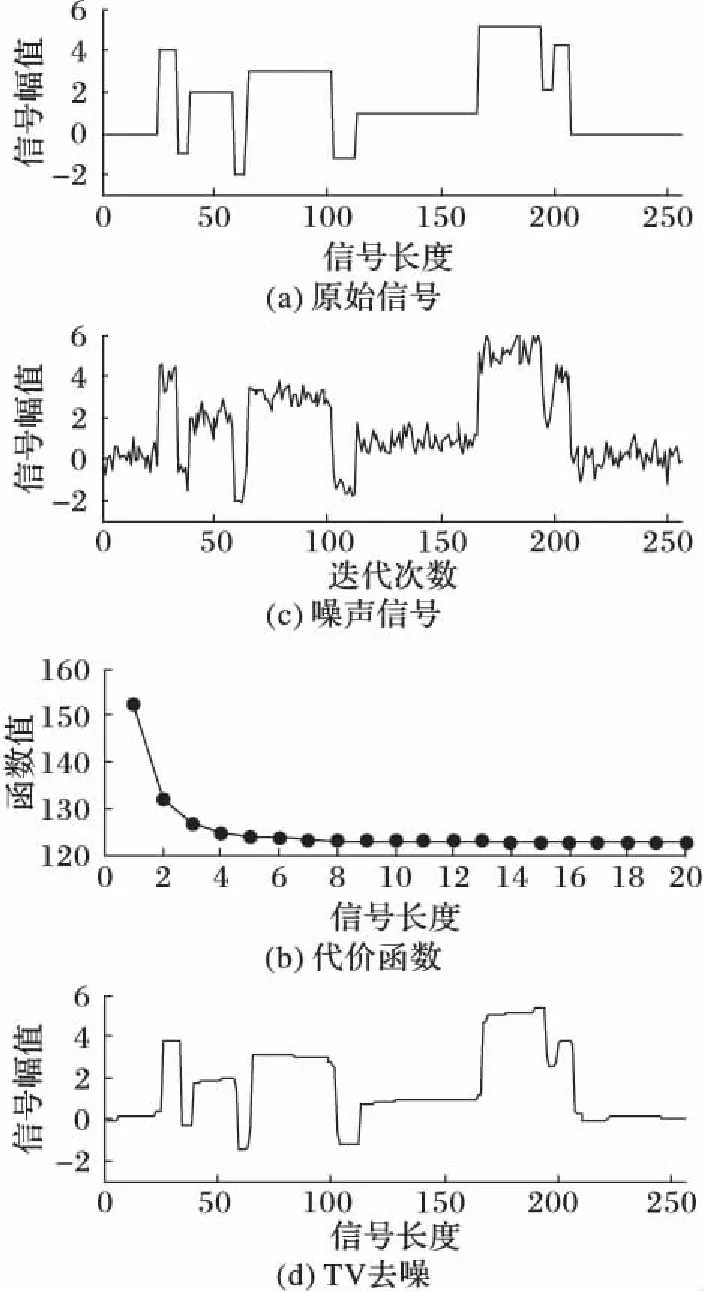
图1 一维信号TV正则化去噪Fig. 1 TV regularization denoising result of one-dimensional signal

图1(a)表示干净的原始信号；图1(b)表示代价函数的解随迭代次数而发生变化，图中明显可以看到当迭代次数为7时，代价函数基本上已经达到最小值；图1(c)的噪声信号中包含干扰所以有不同程度的起伏波动；图1(d)的TV去噪结果基本上接近原始信号，明显去掉了噪声信号中的起伏波纹，即干扰信号。然而，TV算子的各向同性造成去噪同时对本身原始信号中的高频信息也过滤掉了，因此在图像去噪中容易造成图像纹理部分过平滑，平滑区域容易产生阶梯效应，不能很好地保持内容结构和细节信息，损失图像的对比度，影响恢复图像的视觉效果。因此如何找到一种有效的图像去噪模型，使它在去除噪声的同时能有效保持细节信息并抑制阶梯效应，成为本文研究的重点。

2 自适应非局部图像去噪模型

非局部均值滤波容易在图像去噪过程中产生块跳跃模糊现象，而总变分正则化又容易造成图像内容的对比度损失和阶梯效应等。因此，本文借鉴Sutour等[14]的思路引入自适应非局部数据保真项，同时在去噪模型中采用双边总变分(Bilateral Total Variation, BTV)正则化[15-16]的变分框架。这种变分正则化项是基于总变分准则和双边滤波的思想，包含对图像像素之间的空间关系以及灰度关系的约束，同时利用像素空间距离和灰度差值对图像进行恢复，相比TV，它在求解过程中计算量小，同时能够比TV更有效地移除噪声和更好地保持图像边缘细节，其函数表达式如下：

(7)

从图2的结果中可以看出,BTV正则化的方法要明显优于Tikhonov正则化和TV正则化的方法。为了进一步说明BTV算子保持图像边缘的优势，图2(f)、(g)是Tikhonov正则化(Laplacian算子)和BTV正则化在图像边缘数据的选择示意图，可以明显看到前者无论在图像平滑部分还是在边缘部分都保持相同的处理(如图2(f)中空心大圆圈所示)，而BTV正则化在图像边缘部分(图2(g)中斜线所示)具有更好的边缘保持能力，它会沿着边缘方向选取算子的大小(如右图中倾斜椭圆所示)，从而选择合适的数据用于边缘像素的正则化求解，因此在去除图像噪声的同时更好地保持了边缘细节信息。

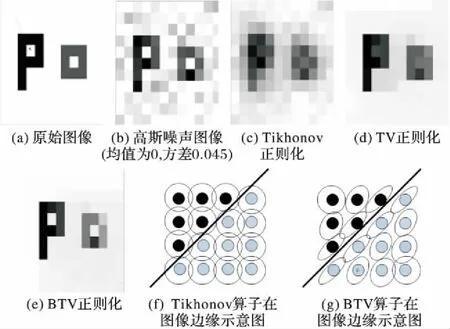
图2 基于变分的正则化方法去噪结果比较Fig. 2 Denoising result comparison of different variation regularization methods

基于上述讨论，本文在Sutour等[14]的基础上展开工作，提出一种新的图像去噪模型，将非局部均值作为最小化能量函数中的数据保真度项，引入双边总变分正则化算子取代全变分正则化的方法，作为最小化能量函数中的正则化项，本文所提图像去噪模型的数学表达式如下：

(8)

(9)

其中，p(fi/uj)是给定噪声观察fi下的真实像素值uj的条件似然估计。为了更好地说明本文提出的图像去噪模型，其算法思想描述如下：

步骤1 输入原始图像u。

步骤2 将图像加入不同类型的污染噪声，成为噪声图像f。

步骤3 计算自适应非局部数据拟合项，采用Sutour等[14]提出的方法。

1)将噪声图像f从空间域转换到Fourier域，在频域定义非局部过程中图像块的形状[17]；

2)采用高斯或双边滤波器对图像块预滤波以提高其鲁棒性；

3)计算空间域图像中所有定义块和相似块在任意方向上的欧氏距离；

4)根据图像内容自适应计算非局部滤波计算中的相应权值w；

5)结合求得的权值系数w，用NLM方法对图像块实现非局部滤波；

6)对于中心权值，采用增量累积的方法实现加权平均；

7)获得加权像素数目的近似值，并实现去滤波拟合操作等。

步骤4 引入双边总分正则化项，设置合适的正则化系数λ，从而在自适应非局部数据保真项和正则化项之间获得良好的平衡。

步骤5 对能量函数最小化通过多步迭代快速算法求解，若满足迭代终止条件(如迭代次数iter=1 000等)则得到最终解，即输出去噪图像。

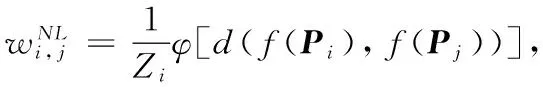
(10)

其中u1和u2表示预期无噪声的图像块，通过自适应的权值计算，得到良好的非局部滤波结果。

3 实验结果与分析

本章将通过实验比较与分析，说明本文所提图像去噪模型的有效性和优越性。实验中所选取的图像数据为标准测试图Lena、自然图像House和Girl(来自TID2013图像库)。这三幅图像所包含的实验图像内容均有显著特点:Lena图像中含有丰富的纹理信息和平滑区域，House和Girl图像中含有丰富的边缘细节和高对比度，可以更好地比较去噪算法的优劣。

本文的实验测试环境为Intel Pentium CPU 2.5 GHz，内存4 GB的HP笔记本电脑，采用Matlab 2012进行仿真测试。为了客观上进一步验证算法的有效性，本文利用峰值信噪比(Peak-Signal-to-Noise Ratio, PSNR)和多尺度结构相似性指标(Multi-Scale Structural Similarity index, MS-SSIM)来评价算法的客观结果，其中PSNR越大，MS-SSIM越接近于1，则说明算法的去噪效果越好。

接下来的实验验证过程中，3.1节会讨论参数设置的原因，模拟仿真实验中分别添加两种程度三种不同类型的噪声到原始图像，同时也采用了真实噪声图像进行去噪处理，通过比较本文提出的去噪算法、自适应NLM滤波[18]去噪结果和基于TV正则化[12]的去噪结果进行比较，从而验证本文提出的图像去噪模型的有效性。

3.1 参数设置

为简化起见，实验过程中非局部数据中滤波参数h=1，相似块的大小设置为7×7，搜索窗的大小设置为21×21。 双边总变分正则化项中平滑系数按照经验取值为α=0.7，在x和y方向的位移l和m分别取为l,m=[-p,p]，其中p=1。此外，正则化参数λ也是该模型中的重要参数，合适的正则化参数λ才能保证数据保真项和正则化项之间的动态平衡，λ太小会在去噪同时引入高频振荡部分，造成图像块状失真；λ过大则会产生过平滑现象，模糊掉图像的细节内容。由于λ取值一般在[0,1]范围内，本文实验中的正则化项参数选取参考了之前研究工作的经验[19]，首先将λ设置为0.05，根据实验结果再手动依次调整，以最后能得到主观视觉最好的结果来确定λ的合适数值。本文实验中设置λ=0.01和λ=0.2两种情况，分别对应正则化系数较为合适和过大两种情况，实验结果中也对两种不同正则化程度的去噪效果作了主观和客观比较，从而更好地反映正则化项对整个去噪结果的影响。

3.2 模拟噪声实验

1)高斯噪声。高斯噪声是一种概率密度函数服从高斯分布(正态分布)的一种噪声，也是图像中常见的噪声，它在图像中的每个像素点上几乎都会出现，但是噪声的深度是随机分布的，可以被认为是各向同性(同方差的)或信号无关的。本实验中分别对图像添加均值为0、标准差为15和35两种不同强度的高斯噪声，以验证本文提出的去噪算法在不同强弱噪声情况下的效果。

从图3中采用λ=0.01和λ=0.2的TV正则化去噪结果可以看出，正则化系数小会造成图像中的噪声没有完全消除，而正则化系数大则会造成过平滑现象。从直观视觉效果角度来判断，本文算法明显优于NLM滤波去噪，如图3中Girl图像的最后一幅局部图中女孩的眼眶周围轮廓明显比其他结果更为清晰，特别是在图4的强噪声实验局部对比结果中，明显可以看到Lena图像中面部颧骨部分和额头部分，NLM滤波会带来一部分的伪影或称为灰度块跳跃现象，而本文提出的方法可以更有效地保持图像的对比度和细节信息。在图4的House图像局部对比结果中，TV正则化去噪结果中明显产生了阶梯效应(如白色方框、椭圆形区域和局部图所示)，而本文算法明显减弱了窗户边缘产生的这些降质伪影，树木细小枝干和房屋区域也更清晰。

2)泊松噪声。泊松噪声是一种广泛存在于医学成像、天文学或者夜间成像的图像中的干扰信号，它是一种与信号有关的噪声，其统计分布特性符合泊松分布模型。本实验中同样往测试图像中分别加入强度为15和35泊松噪声，从而更好地验证本文算法去除图像噪声同时保留细节信息的有效性。

从图5可以看出采用TV正则化在λ=0.01和λ=0.2时的去噪结果完全不同，λ较小时包含大量噪声，而λ较大时在帽子羽毛部分明显产生过度平滑和阶梯效应，其效果是远远不如NLM滤波和本文算法的去噪结果；而在人物面部鼻梁、嘴唇上方和眼睛下方等区域，NLM滤波会造成灰度跳跃等伪影，而本文算法去噪结果更接近于真实的原始图像。图6是强泊松噪声的去噪结果，从Lena图像的结果比较明显可以看出本文算法优于其他对比算法；而从House图像的结果可以看出，NLM算法的结果中房屋的墙面和窗户的边缘有明显的灰度跳跃和寄生波纹存在，而本文算法结果中则明显减弱了波纹伪影，窗户的边缘轮廓线部分也更清晰。

图3 弱高斯噪声去噪结果对比Fig. 3 Denoising results of weak Gaussian noisy image by different methods

图4 强高斯噪声去噪结果对比Fig. 4 Denoising results of strong Gaussian noisy image by different methods

图5 弱泊松噪声去噪结果对比Fig. 5 Denoising results of weak Possion noisy image by different methods

图6 强泊松噪声去噪结果对比Fig. 6 Denoising results of strong Possion noisy image by different methods

3)混合噪声。在混合噪声的模拟实验中，原始图像中混合添加了高斯、泊松和椒盐等三种噪声，强噪声和弱噪声的程度分别设置为5和15。由于篇幅有限，此处只给出仿真实验中对应弱混合噪声部分的实验结果，如图7所示，其他去噪结果在表1对应的客观评价结果中给出对比验证。

从图7上Lena图像实验结果可以明显看出，NLM滤波和本文算法的效果要优于TV正则化去噪的方法，在NLM去噪和本文算法去噪的局部效果图对比下，可以看到在人物面部的额头部分和面部颧骨部分，NLM滤波会产生灰度跳跃和纹理不清晰的状况，而本文算法更好地保护了图像的对比度和细节信息。另外，从图7的House图像在TV正则化系数λ=0.01和λ=0.2的去噪结果可以明显看到，λ=0.01时图像中树叶、天空和房屋墙面部分都含有明显的噪声，而λ=0.2时图像中树叶和屋顶部分被过分平滑；从NLM滤波去噪局部效果可以看出，其房屋顶部和窗户的边缘部分都不如本文算法效果好，因此本文算法在去噪同时能较好地自适应于图像的结构特性。

由于篇幅所限,实验中没有全部给出Girl图像的主观结果，而为了更好地说明本文算法的有效性，在对比上述主观效果的同时本文也给出了各种算法的客观评价指标比较，如表1所示(表1中P值表示PSNR指标值，M值表示MS-SSIM值)。从表1中PSNR和MS-SSIM的数值对比可以看出，随着各种不同类型噪声等级的增加，各类去噪方法的PSNR值和MS-SSIM值都有所下降，以含高斯噪声的Lena图像为例，同样采用TV正则化去噪(λ=0.2)，强噪声和弱噪声的PSNR值相差约5 dB；MS-SSIM值相差约0.01。表1中对不同类型与强度噪声处理的实验结果可以看出，本文提出的去噪模型在客观评价数值上与NLM滤波结果较为接近，而该NLM滤波在本文模型中是作为数据拟合项计算的一部分，并且在绝大多数情况下本文算法都能够得到更好的效果，PSNR值提高约0.1～0.6 dB，在MS-SSIM值上也有所提升(如表1中加粗字体标注)，因此明显优于其他去噪算法得到的结果。

图7 混合弱噪声去噪实验结果Fig. 7 Denoising results of hybrid noise image表1 各算法去噪性能的客观定量指标比较Tab. 1 Objective quantitative indexes of denoising performance by different methods

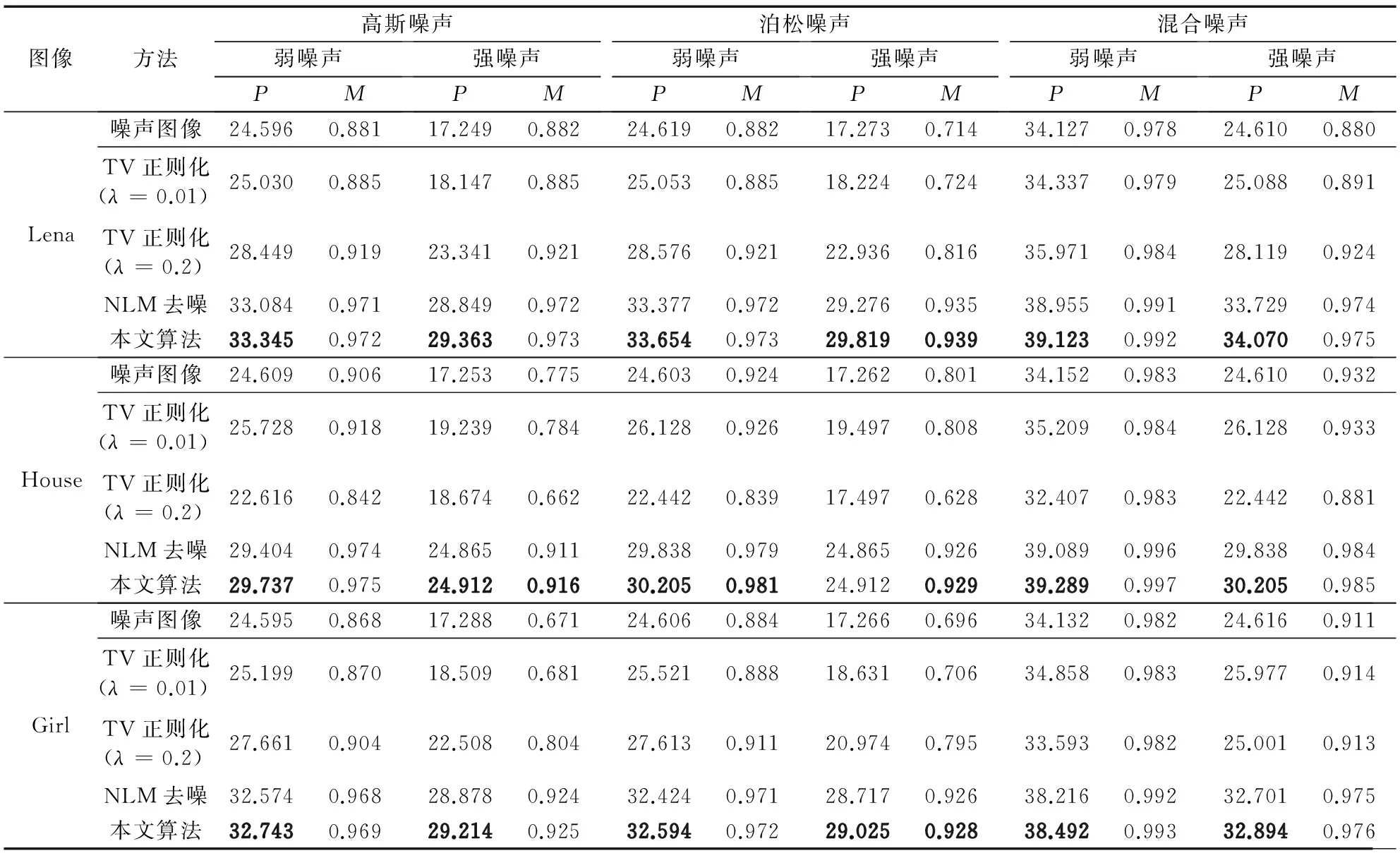
图像方法高斯噪声弱噪声PM强噪声PM泊松噪声弱噪声PM强噪声PM混合噪声弱噪声PM强噪声PMLena噪声图像24.5960.88117.2490.88224.6190.88217.2730.71434.1270.97824.6100.880TV正则化(λ=0.01)25.0300.88518.1470.88525.0530.88518.2240.72434.3370.97925.0880.891TV正则化(λ=0.2)28.4490.91923.3410.92128.5760.92122.9360.81635.9710.98428.1190.924NLM去噪33.0840.97128.8490.97233.3770.97229.2760.93538.9550.99133.7290.974本文算法33.3450.97229.3630.97333.6540.97329.8190.93939.1230.99234.0700.975House噪声图像24.6090.90617.2530.77524.6030.92417.2620.80134.1520.98324.6100.932TV正则化(λ=0.01)25.7280.91819.2390.78426.1280.92619.4970.80835.2090.98426.1280.933TV正则化(λ=0.2)22.6160.84218.6740.66222.4420.83917.4970.62832.4070.98322.4420.881NLM去噪29.4040.97424.8650.91129.8380.97924.8650.92639.0890.99629.8380.984本文算法29.7370.97524.9120.91630.2050.98124.9120.92939.2890.99730.2050.985Girl噪声图像24.5950.86817.2880.67124.6060.88417.2660.69634.1320.98224.6160.911TV正则化(λ=0.01)25.1990.87018.5090.68125.5210.88818.6310.70634.8580.98325.9770.914TV正则化(λ=0.2)27.6610.90422.5080.80427.6130.91120.9740.79533.5930.98225.0010.913NLM去噪32.5740.96828.8780.92432.4240.97128.7170.92638.2160.99232.7010.975本文算法32.7430.96929.2140.92532.5940.97229.0250.92838.4920.99332.8940.976

3.3 真实噪声实验

采用数字照相机等图像采集设备获取信息时，图像噪声是在成像过程图像亮度或颜色信息的随机变化，它可能由数字采集设备本身或者自然场景所产生，一般在亮度较低的采集环境中更明显。本实验中采用真实的噪声图像以更进一步验证本文所提去噪模型的有效性，实验中采用的真实噪声图像1来源于维基网页https://en.wikipedia.org/wiki/ Image_noise，真实噪声图像2来源于http://www.adorama.com/alc/0012955/article/FAQ-What-is-Noise-in-a-Digital-Photograph，由ISO 2000 的Canon 7D拍摄于Kennedy Space Center，图像3是采用华为G610-C00手机在夜晚室内光照较暗的环境下拍摄得到。

为了更好地突出显示去噪效果，在图8中真实图像1的局部对比图采用了反色处理。由图8真实噪声图像的实验结果可以明显看出，TV正则化无法有效去除图像中存在的各种噪声，特别是在细节图中可以看到图像中仍然包含有大量的噪声，严重损坏了图像质量。相比TV正则化，NLM算法能够非常明显地去除图像中包含的噪声，得到较好的去噪结果。本文算法分别做了λ=0.01和λ=0.2两种不同正则化情况下的实验。从实验结果可以明显看到，在相同正则化系数的情况下，本文算法比NLM能得到更好的去噪效果，同时又能良好地保持图像的关键细节信息(如图8中真实图像1的书本和柱子的边缘；真实图像2中球的正面及右上方球杆部分；以及真实图像3中书本背景凹凸纹理部分)。而当正则化系数λ变大以后，从图中可以明显看到虽然同样能得到良好的去噪效果，但与此同时损失了许多图像中本来应该保持的细节(如图8真实图像1中书本之间层叠的细节；真实图像2中球体上的孔洞)，特别是真实图像3中书本背景部分的凹凸纹理基本上看不见了，变成了平滑模糊的背景。

图8 真实噪声图像去噪效果对比Fig. 8 Denoising result comparison of real noisy images by different methods

从上述真实噪声图像的实验结果可以明显看出，非局部均值滤波不仅有图像块平滑效应，在图像边缘也不能达到很好的去噪效果；添加BTV去噪模型不仅比NLM获得了更好的去噪效果，良好地保持了图像的边缘细节信息，同时又避免了单纯正则化去噪中存在的阶梯效应和对比度损失等问题，得到了较好的去噪结果。

4 结语

为了克服传统NLM滤波容易造成的过平滑、奇异结构残留噪声以及传统TV正则化方法导致对比度损失和灰度跳跃等现象，本文提出一种自适应非局部均值滤波和双边正则化算子相结合的图像去噪模型，以自适应非局部概率分布函数的自然对数作为数据保真项，利用正则化系数平衡数据保真项和正则化项，利用最小化能量函数通过多步迭代快速算法对模型进行求解。实验部分对含有不同类型和不同程度的模拟噪声图像及真实噪声图像进行处理，采用本文模型和其他几种常用方法进行比较，结果表明本文方法能够更好地克服去噪过程中容易造成的阶梯效应和过模糊等现象，对噪声的抑制也更为稳健，从而说明本文算法无论是在主观视觉效果上还是在客观评价指标上都有明显的改善。在本文的工作基础上，后续工作希望进一步将提出的去噪模型拓展到颜色滤波阵列(Color Filter Array, CFA)图像、彩色图像或更高维数据的处理，从而在图像分割、重建和识别等方面得到更好的实际应用。

References)

[1] 张峥嵘，黄丽丽，费选,等. 非局部TV正则化的图像泊松去噪模型与算法[J]. 系统仿真学报，2014,26(9):2110-2115. (ZHANG Z R, HUANG L L, FEI X, et al. Image Possion denoising model and algorithm based on nonlocal TV regularization [J]. Journal of System Simulation, 2014, 26(9): 2110-2115.)

[2] 胡学刚,李妤. 基于分数阶变分的图像泊松去噪模型[J]. 计算机应用,2013,33(4):1100-1102. (HU X G, LI Y. Improved image Possion denoising model based on fractional variation [J]. Journal of Computer Applications, 2013, 33(4): 1100-1102.)

[3] BUADES A, COLL B, MOREL J-M. A review of image denoising algorithm, with a new one [J]. SIAM Journal on Multiscale Modeling and Simulation: A SIAM Interdisciplinary Journal, 2005, 4(2): 490-530.

[4] BUADES A, COLL B, MOREL J-M. Non-local image and movie denoising [J]. International Journal of Computer Vision, 2007, 76(2):123-139.

[5] 杨爱萍,田玉珍,何宇清,等.基于改进K-SVD和非局部正则化的图像去噪[J].计算机工程，2015,41(5): 249-253. (YANG A P, TIAN Y Z, HE Y Q, et al. Image denoising based on improvedK-SVD and non-local regularization [J]. Computer Engineering, 2015, 5: 249-253.)

[6] 费选,违志辉,肖亮,等.优化加权TV的复合正则化压缩感知图像重建[J].中国图象图形学报,2014,19(2):211-218. (FEI X, WEI Z H, XIAO L, et al. Compound regularized compressed sensing image reconstruction based on optimal reweighted TV [J]. Journal of Image and Graphics, 2014, 19(2): 211-218.)

[7] 耿海, 何小卫, 樊骏笠. 基于可变指数及L1保真项的图像去噪算法[J].计算机应用，2013,33(10):2931-2934. (GENG H, HE X W, FAN J L. Image denoising algorithm with variable exponent regularization and L1 fidelity [J]. Journal of Computer Applications, 2013, 33(10): 2931-2934.)

[8] 史加荣, 郑秀云,杨威.不完全鲁棒主成分分析的正则化方法及其在背景建模中的应用[J].计算机应用,2015,35(10):2824-2827. (SHI J R, ZHENG X Y, YANG W. Regularized approach for incomplete robust principal component analysis and its application in background modeling [J]. Journal of Computer Applications, 2015, 35(10): 2824-2827.)

[9] 刘红丽,刘伟锋,王延江.Hessian正则化Logistic回归模型[J].计算机工程与应用,2016,52(5):236-240. (LIU H L, LIU W F, WANG Y J. Hessian regularized logistic regression [J]. Computer Engineering and Applications, 2016, 52(5): 236-240.)

[10] 冀常鹏, 姬红红, 郭伟平. 变阶变正则化APA在回声抵消中的应用[J].计算机工程与应用,2014,50(15):168-171. (JI C P, JI H H, GUO W P. APA with evolving order and variable regularization for echo cancellation [J]. Computer Engineering and Applications, 2014, 50(15): 168-171.)

[11] TIKHONOV A N, ARSENIN V Y. Solutions of ill-posed problems [J]. Mathematics and Computation, 1978, 32(144): 1320-1322.

[12] RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms [J]. Physica D: Nolinear Phenomena, 1992, 60(1/2/3/4): 259-268.

[13] SELESNICK I W, PAREKH A, BAYRAM I. Convex 1-D total variation denoising with non-convex regularization [J]. IEEE Signal Processing Letters, 2015, 22(2): 141-144.

[14] SUTOUR C, DELEDALLE C-A, AUJOL J-F. Adaptive regularization of the NL-means: application to image and video denoising [J]. IEEE Transaction on Image Processing, 2014, 23(8): 3506-3521.

[15] FARSIU S, ROBINSON D, ELAD M, et al. Fast and robust multiframe super resolution [J]. IEEE Transactions on Image Processing, 2004, 13(10): 1327-1344.

[16] FARSIU S, ROBINSON D, ELAD M, et al. Robust shift and add approach to superresolution[C]// Proceeding of SPIE International Conference on Applications of Digital Signal and Image Processing XXVI, SPIE 5203. Bellingham, WA: SPIE, 2003: 121-130.

[17] DELEDALLE C-A, DUVAL V, SALMON J. Non-Local Methods with Shape-Adaptive Patches (NLM-SAP) [J]. Journal of Mathematical Imaging and Vision, 2011, 43(2): 103-120.

[18] DELEDALLE C A, DENIS L, TUPIN F, et al. NL-SAR: a unified non-local framework for resolution-preserving in SAR denoising [J]. IEEE Transaction on Geoscience and Remote Sensing, 2015, 53(4): 2021-2038.

[19] GUO L, HE X H, CHEN W L, et al. A pioneering video-to-video super-resolution reconstruction algorithm based on segmentation and space-time regularization [J]. The Imaging Science Journal, 2014, 62(4): 236-250.

This work is partially supported by the National Natural Science Foundation of China (61663008, 61463014, 61562025), the National Key Technology R&D Program (2015BAK27B01), the Natural Science Foundation of Hubei Province (2015CFC781, 2014CFB612, 2012FFC02601), the Scientific Research Project of Department of Education of Sichuan Province (15ZB0039), the Foundation of China Scholarship Council, the Foundation of PhD Technology Project of Hubei University for Nationalities (MY2014B018).

GUOLi, born in 1978, Ph. D., associate professor. Her research interests include image processing and recognition, computer vision, information display.

LIAOYu, born in 1979, Ph. D. candidate, associate professor. His research interests include signal and information processing, optical communication.

LIMin, born in 1981, M. S., lecturer. Her research interests include signal and information processing.

YUANHailin, born in 1967, M. S., professor. His research interests include embedded system analysis.

LIJun, born in 1972, M. S., professor. His research interests include computer graphics, digital image processing.

Imagedenoisingmodelwithadaptivenon-localdata-fidelitytermandbilateraltotalvariation

GUO Li1,2，LIAO Yu1*，LI Min1，YUAN Hailin1，LI Jun1

(1.CollegeofInformationEngineering,HubeiUniversityforNationalities,EnshiHubei445000,China；2.FacultyofMathematicsandComputerScience,UniversityofGroningen,Groningen9747AG,theNetherlands)

Aiming at the problems of over-smoothing, singular structure residual noise, contrast loss and stair effect of common denoising methods, an image denoising model with adaptive non-local data fidelity and bilateral total variation regularization was proposed, which provides an adaptive non-local regularization energy function and the corresponding variation framework. Firstly, the data fidelity term was obtained by non-local means filter with adaptive weighting method. Secondly, the bilateral total variation regularization was introduced in this framework, and a regularization factor was used to balance the data fidelity term and the regularization term. At last, the optimal solutions for different noise statistics were obtained by minimizing the energy function, so as to achieve the purpose of reducing residual noise and correcting excessive smoothing. The theoretical analysis and simulation results on simulated noise images and real noise images show that the proposed image denoising model can deal with different statistical noise in image, and the Peak-Signal-to-Noise Ratio (PSNR) of it can be increased by up to 0.6 dB when compared with the adaptive non-local means filter; when compared with the total variation regularization algorithm, the subjective visual effect of the proposed model was improved obviously and the details of image texture and edges was protected very well when denoising, and the PSNR was increased by up to 10 dB, the Multi-Scale Structural Similarity index (MS-SSIM) was increased by 0.3. Therefore, the proposed denoising model can theoretically better deal with the noise and the high frequency detail information of the image, and has good practical application value in the fields of video and image resolution enhancement.

adaptive non-local means; data fidelity term; regularization function; bilateral total variation; image denoising

TP391.9; TN911.73

A

2017- 01- 13;

2017- 03- 20。

国家自然科学基金资助项目(61663008, 61463014, 61562025)；国家科技支撑计划项目(2015BAK27B01)；湖北省自然科学基金资助项目(2015CFC781, 2014CFB612, 2012FFC02601)；四川省教育厅科研项目(15ZB0039)；国家留学基金委地方合作项目；湖北民族学院博士启动基金资助项目(MY2014B018)。

郭黎(1978—)，女，湖北黄冈人，副教授，博士，主要研究方向：图像处理与识别、计算机视觉、信息显示； 廖宇(1979—)，男，湖北建始人，副教授，博士研究生，主要研究方向：信号与信息处理、光通信； 李敏(1981—)，女，湖北宣恩人，讲师，硕士，主要研究方向：信号与信息处理； 袁海林(1967—)，男，湖北恩施人，教授，硕士，主要研究方向：嵌入式系统分析； 李军(1971—)，男，湖北利川人，教授，硕士，主要研究方向：计算机图形学、数字图像处理。

1001- 9081(2017)08- 2334- 09

10.11772/j.issn.1001- 9081.2017.08.2334