基于网络表示学习与随机游走的链路预测算法

刘 思，刘 海，2，陈启买，贺超波

(1.华南师范大学 计算机学院，广州 510631； 2.广东省高性能计算重点实验室，广州 510033；3.仲恺农业工程学院 信息科学与技术学院，广州 510225)

(*通信作者电子邮箱liuhai@m.scnu.edu.cn)

基于网络表示学习与随机游走的链路预测算法

刘 思1，刘 海1，2*，陈启买1，贺超波3

(1.华南师范大学 计算机学院，广州 510631； 2.广东省高性能计算重点实验室，广州 510033；3.仲恺农业工程学院 信息科学与技术学院，广州 510225)

(*通信作者电子邮箱liuhai@m.scnu.edu.cn)

现有的基于随机游走链路预测指标在无权网络上的转移过程存在较强随机性，没有考虑在网络结构上不同邻居节点间的相似性对转移概率的作用。针对此问题，提出一种基于网络表示学习与随机游走的链路预测算法。首先，通过基于深度学习的网络表示学习算法——DeepWalk学习网络节点的潜在结构特征，将网络中的各节点表征到低维向量空间；然后，在重启随机游走(RWR)和局部随机游走(LRW)算法的随机游走过程中融合各邻居节点在向量空间上的相似性，重新定义出邻居节点间的转移概率；最后，在5个真实数据集上进行大量实验验证。实验结果表明：相比8种具有代表性的基于网络结构的链路预测基准算法，所提算法链路预测结果的AUC值均有提升，最高达3.34%。

链路预测；相似性；重启随机游走；局部随机游走；网络表示学习

0 引言

现实世界中存在大量的复杂系统都可以通过网络形式来体现，其节点代表真实系统中不同的实体，连边代表实体间的联系。链路预测是指通过已知的网络结构和属性等信息,预测网络中尚未产生连接的两个节点间产生连接的可能性[1]。链路预测在复杂网络和信息科学之间起着重要的桥梁作用，对于链路预测研究具有重要的理论价值与实际应用。理论上，它可以帮助人们很好地理解复杂网络的演化机制[2]；在实际应用方面，它可以在生物网络中揭示隐含的相互作用关系以指导实验，在社交网络中推荐用户最可能认识的好友，还可以在电子商务中推荐顾客个性化的商品等。近年来，关于复杂网络中链路预测的研究越来越受到国内外学者的广泛关注[3]。

链路预测最直观的假设是，如果两个节点之间越相似，它们之间最有可能产生连边。基于这种假设，链路预测的基本问题是如何刻画和计算节点之间的相似性。目前，主要存在如下刻画节点相似性的方法。

1)基于节点属性的链路预测方法，其主要是利用节点的外部属性和标签信息来刻画节点之间的相似性。例如，如果两人之间具有相同的学校、工作和兴趣，则可以认为他们之间存在较高的相似性。虽然应用节点属性等信息可以取得不错的预测效果，但在很多情况下，节点的属性信息不易获取且伴有较多噪声，导致无法保证信息的可靠性，同时对于如何甄别哪些属性对于特定的链路预测场景是有效的以及多大程度有效也是一个重要问题。

2)基于网络结构的链路预测方法。近年来，该方法得到了越来越多的关注[3]。相对于节点属性而言，网络结构信息的获取较容易且更可靠，同时对于结构相似的网络具有较高的适用性。预测精确度的高低很大程度上取决于能否很好地选取网络结构特征。当前存在很多基于网络结构相似性的链路预测指标，其中，基于局部信息的相似性指标主要包括共同邻居指标(Common Neighbors, CN)、Salton指标、Jaccard指标[4]、Sorenson指标、大度节点有利指标(Hub Promoted Index, HPI)、大度节点不利指标(Hub Depressed Index, HDI)、LHN-Ⅰ指标、Adamic-Adar指标[5]、资源分配(Resource Allocation, RA)指标和优先偏好(Preferential Attachment, PA)[6]指标等。基于路径的相似性指标主要包括局部路径(Local Path, LP)指标[7-8]、Katz指标[9]和LHN-Ⅱ(Leicht-Holme-Newman-Ⅱ)指标[10]。基于随机游走的相似性指标包括平均通勤时间(Average Commute Time, ACT)[11]、基于随机游走的余弦相似性(Cos+)指标、有重启的随机游走(Random Walk with Restart, RWR)指标[12]、SimRank(SimR)指标、局部随机游走(Local Random Walk, LRW)指标[13]和有叠加效应的局部随机游走(Superposed Random Walk, SRW)指标[13]。吕琳媛[1]在一些真实的网络数据集上进行实验并总结对比了上述各种基于网络结构相似性指标的预测结果，发现基于随机游走的相似性指标具有更高的准确性，尤其是基于局部随机游走的相似性指标具有更低的计算复杂度和更高的预测精确度。

3)基于网络结构和节点属性融合的链路预测方法，其综合考虑了节点的属性和网络结构信息来刻画节点之间的相似性。Cherry等[14]在社交网络Twitter中抽取出用户不同类型的属性信息和多种网络结构特征，对用户间的联系强度和社交关系建模，最后用于刻画用户之间的相似度来提高链路预测的效果。

网络表示学习是指对网络特征进行学习，用低维向量表示网络节点[15]。近几年，深度学习在特征表示学习上取得了巨大的进展[16]。在自然语言处理领域中，以基于深度学习的Word2vec模型[17]为代表的模型在词向量表示方面取得了很好的效果，从而启发了大家应用深度学习在网络表示学习方面的研究。目前这方面的研究也取得了一些较大的进展，其中一个最具有代表性的基于深度学习的模型是DeepWalk[18]，它正是基于当前最流行的词向量表示模型Word2vec。DeepWalk能够很好地学习网络结构特征，将网络中的每个节点用一定维度的连续向量表征出来，同时能够很好地捕捉网络邻居节点的相似性以及社区关系。

现有的基于随机游走的链路预测方法，在未知网络节点属性与权重信息的情形下，邻居节点间的转移过程仅考虑了节点度之类的局部信息，具有一定的盲目性。例如，基于重启随机游走和基于局部随机游走的链路预测指标仅考虑了节点度进行随机转移。为此，本文在基于随机游走的相似性指标基础上，利用网络表示学习方法DeepWalk学习网络各节点的潜在网络结构特征，将其表征到低维向量空间中，并通过各节点在向量空间上的相似性来度量各节点在潜在网络结构特征上的相似性，旨在随机游走的转移过程中融合各节点间的潜在网络结构相似性，有效地度量各邻居节点间的转移概率。最后通过与众链路预测基准算法进行实验对比，结果显示本文提出的链路预测算法能取得很好的预测效果。

1 相关工作

1.1 重启随机游走指标

重启随机游走(RWR)指标可以看作是PageRank算法[19]在链路预测问题上的拓展应用，其基本思想是假设随机游走粒子在网络上某个节点位置开始运动，每游走到一个节点时，都能以一定的概率返回初始节点。

假设随机游走粒子转移到任意邻居节点的概率为α，返回初始节点的概率为1-α。P为概率转移矩阵，其元素Pxy=axy/kx表示粒子从节点x游走到节点y的概率。其中：如果x和y之间相连，则αxy=1，否则αxy=0；kx表示节点x的度。若粒子在初始时刻位于节点x处，则在t+1时刻粒子转移到网络上各节点的概率向量为：

Dx(t+1)=α·PTDx(t)+(1-α)ex

(1)

其中ex是表示初始状态。式(2)的稳态解为：

Dx=(1-α)(1-αPT)-1ex

(2)

其中元素dxy表示从节点x到达节点y时处于稳态的概率，由此，节点x和节点y的相似性定义为：

(3)

1.2 局部随机游走指标

局部随机游走指标(LRW)是由Liu等[13]提出的一种基于网络局部结构信息的随机游走相似性指标，用于解决基于全局的随机游走相似性指标存在计算复杂度过高以致难以在大规模网络上应用等问题，同时也具有较高的预测准确度。它的主要特点是在随机游走过程中只考虑有限步数。

假设一个随机游走粒子从节点x出发，πx(t)表示此粒子从节点x经游走t步到达网络上其余各节点概率的N×1维向量，有：

πx(t)=pTπx(t-1)

(4)

其中πx(0)=ex。通常根据网络各节点的重要性来分配其初始资源分布，此处假定各个节点的初始资源分布为qx，那么，节点x与任意节点y基于t步随机游走的相似性定义为：

(5)

1.3 Word2vec模型

Word2vec是由Mikolov等[17]在2013年提出的一种快速学习词向量表示的模型，其基本思想是利用神经网络通过训练，将文本中的单词转换到低维、稠密的实数向量空间中，通过向量空间中的向量运算来简化文本内容上的处理。例如文本的语义相似度可以通过向量空间上的相似度来衡量，可以用于自然语言处理中的很多工作中，包括同义词寻找、词性分析等。

Word2vec主要使用了两种语言模型：连续词袋模型(Continuous Bag-Of-Words model, CBOW)和Skip-Gram(continuous Skip-Gram model)，它们在借鉴自然语言处理模型(Neural Network Language Model， NNLM)[20]的基础上进行了简化以便于计算，是包含了输入层、投影层和输出层的三层神经网络，如图1所示。

训练过程可以简述为：若给定某一语料库，使用一个固定长度为c的滑动窗口遍历整个预料库，每次从整个语料库中抽取出一段语料进行训练，假设c=2，则每次的训练语料为Wt-2Wt-1WtWt+1Wt+2。CBOW模型的基本思想是使用某一词Wt的上下文Wt-2Wt-1Wt+1Wt+2来预测词Wt，训练过程如图1所示，输入层为Wt的上下文Wt-2Wt-1Wt+1Wt+2各个词向量，投影层是对输入层所有词向量进行累加求和，输出层通常采用Hierarchical Softmax[21]或者Negative Sampling算法来表征已知上下文Wt-2Wt-1Wt+1Wt+2的条件下Wt出现的概率。Skip-Gram模型的基本思想与CBOW模型相反，是使用某一词Wt来预测其上下文Wt-2Wt-1Wt+1Wt+2，训练过程与CBOW模型类型类似。

2 基于网络表示学习与随机游走的链路预测

通过1.1节和1.2节对RWR与LRW等两种基于随机游走的链路预测指标的转移过程进行分析，发现转移矩阵P在随机游走过程中是一个关键因素，对最后预测的结果产生重要影响。

考虑在无权网络G(V,E)中，其中：V代表节点集合，E代表连边集合，不存在自连接。LRW指标和RWR指标在随机游走过程中，当游走到任意节点x时，选择任意邻居节点y的作为下一步游走的概率均是1/kx。其中：kx表示节点的度，具有较强的随机性，没有考虑到不同节点间的潜在网络结构相似性对转移过程的影响。本文认为，在随机游走过程中，在网络结构上相似度更高的两节点之间应该有更高的转移概率。

2.1 DeepWalk模型

DeepWalk是由Perozzi等[18]提出的一种基于深度学习的网络表示学习模型。通过观察发现，如果在一个服从幂律分布的网络(即无标度网络)上进行随机游走，其网络节点被访问的频率也服从幂律分布，而这与自然语言中的词频同样服从幂律分布是类似的。受此启发，将网络中的节点类比成自然语言中的一个词，而将网络上一次随机游走过程中产生的节点访问序列类比成自然语言中的句子，再在此基础上结合Word2vec模型将网络上进行随机游走产生的节点访问序列当作Skip-Gram模型的输入，采用随机梯度下降和反向传播算法对节点表示向量进行优化，最后训练生成每个节点最优的向量表示。DeepWalk算法的描述框架如下所示：

输入 网络G(V,E)，滑动窗口大小ω，向量空间维数d，重新随机游走遍历次数γ，每次随机游走遍历步长t。

输出 节点表示向量矩阵Φ∈R|V|×d。

1)初始化Φ，使其服从均匀分布。

2)将网络节点构造成一棵二叉树T。

3)将网络节点随机排序放入到集合ϑ。

4)从属于集合ϑ的每个节点vi开始，在网络G上进行步长为t的随机游走，产生节点Wvi的访问序列Wvi。

5)SkipGram(Φ,Wvi,ω)，即对Wvi用Skip-Gram算法更新节点向量表示。

6)一直重复步骤3)～6)γ次。

2.2 融合DeepWalk模型与随机游走的链路预测

通过观察DeepWalk模型的网络节点向量的表示学习过程，发现它综合考虑到了节点的“上下文信息”，即节点周围的网络结构，并通过深度学习方法不断训练节点的网络结构特征的最优向量表示，训练出的节点在向量空间上的相似性可以很好地表征节点在网络结构上的潜在相似性。受DeepWalk模型启发，本文在基于随机游走的转移矩阵P中融合DeepWalk所生成的各节点向量表示的相似性，然后进行转移更新，最终计算出不同节点间的相似度，这样可以很好地体现出节点在潜在网络结构上的相似度对随机游走转移过程的影响。

首先使用DeepWalk算法生成网络中每个节点的向量表示，假定Φ(x)=[x1,x2,…,xd]表示任意节点x的向量，Φ(y)=[y1,y2,…,yd]表示任意节点y的向量。由于欧氏距离被广泛采用来衡量多维空间中两点间的距离，所以本文也利用各节点在多维空间上的欧氏距离来表征各节点在潜在网络结构上的相似度，并给出定义1。

定义1 网络中任意节点x和任意节点y之间的潜在网络结构相似性为：

DWSim(x,y)=Euclidean(Φ(x),Φ(y))=

(6)

为了在随机游走的转移过程中保持一定的随机性，在随机游走的每一步转移过程中按一定比例融合各节点间的潜在网络结构相似性，并给出定义2。

定义2 任意节点x与其任意邻居节点y之间的转移概率为：

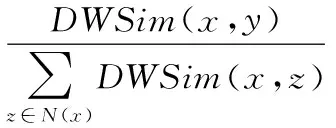
(7)

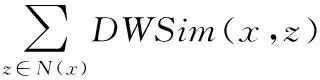
3 实验结果及分析

3.1 实验数据集

本文实验采用了分别在5个不同领域具有代表性的真实网络数据集，忽略网络连边的权重与方向，分别如下:

1)USAir网络(http://vlado.fmf.uni-lj.si/pub/networks/data)，由332个机场的之间航线构成的网络，包含2 126条航线。

2)Jazz网络(http://www.linkprediction.org/index.php/link/resource/data)，由198个音乐家构成的合作网络，包含2 742个音乐家的合作关系。

3)Metabolic网络(http://www.linkprediction.org/index.php/link/resource/data)，其中的节点代表线虫的代谢物，连边代表代谢物之间能直接参与的酶催化生化反应，包含453种线虫代谢物。

4)NetScience网络(networkrepository.com/network.php)，由1 589个科学家的合作关系构成的网络，包含268个连通集。本实验选取最大的连通集，包含379个节点。

5)Facebook社交网络(snap.stanford.edu/data/index.html)，是从Facebook中抽取出的部分社交网络，包括4 039个用户，其中的节点代表用户，连边代表用户之间的好友关系。

表1进一步列出了这5个数据集的网络拓扑结构特征，其中：N表示节点数，M表示连边数，〈K〉表示平均度，〈C〉表示平均聚集系数，D表示网络直径。

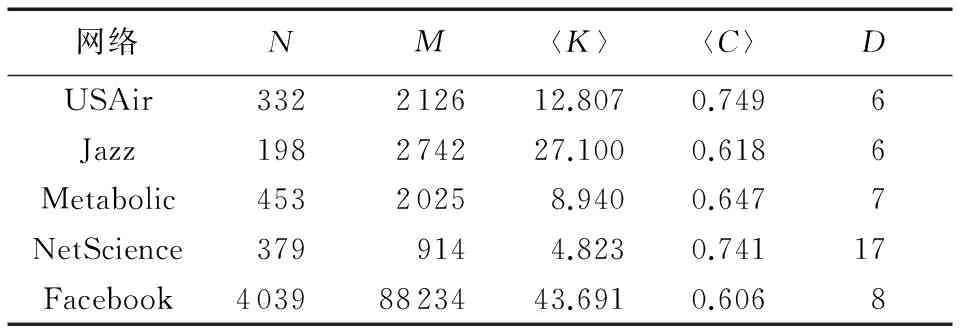
表1 各数据集的拓扑结构特征Tab. 1 Topological structure features of each dataset

3.2 评价指标

为了评估算法的准确性，实验将数据集随机且独立地划分为训练集和测试集，90%用作训练集，10%用作测试集，同时保证训练集和测试集中的网络具有连通性。本文实验采用AUC(Area Under the receiver operating characteristic Curve)指标[22]来评价算法的准确性。

在链路预测算法计算出所有节点间存在连边的分数值之后，AUC指标可以描述为在测试集中随机选择一条存在连边的分数值比随机选择一条不存在连边的分数值高的概率。这样独立重复比较n次，在n次中，如果有n′次在测试集中存在连边的分数比不存在连边的分数值高，有n″次在测试集中存在连边的分数值与不存在连边的分数值相等，则AUC值可以定义为：

AUC=(n′+0.5n″)/n

(8)

通常，评分算法计算出的AUC值最少应大于0.5。AUC值越高，算法的精确度就越高，最高不超过1。

3.3 实验环境与实验参数

实验环境：Windows 7操作系统，DeepWalk模型算法采用Python 2.7实现，所提算法和各对比链路预测算法均在Matlab R2015a上实现。

实验参数设置如下：

1)DeepWalk模型算法参数：ω=5,γ=10,t=40,d=64。

2)式(7)的调节参数β。实验通过β在区间[0,1]上的不同取值，观察β取值对预测结果的影响，整体上，β取值为0.75在所有数据集上都能取得较好的实验效果。

3)重启因子α。通常α取值为0.9有着较优的效果，因此，本文设置α=0.9。

4)DWLRW和LRW随机步长t。随机步长对实验的预测效果起重要作用，实验通过在区间[2,20]上不同的取值，观察DWLRW和LRW在不同数据集上AUC值的变化，如图2所示，t的不同取值对AUC值产生一定影响，在本文实验中取最优步长的AUC值进行对比，在表2中DWLRW和LRW算法的AUC值后括号内的数值表示在各数据集上的最优步长取值。

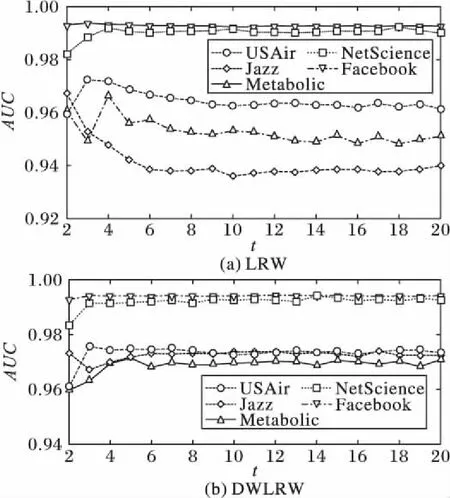
图2 AUC值随参数t的影响Fig. 2 Influence of parameter t on AUC

3.4 基准方法

本文所提算法是一种基于网络结构的链路预测方法。除了基于重启随机游走方法与基于局部随机游走方法外，本文还将最常用的6种基于网络结构的方法作为基准进行性能对比，其中包含基于网络局部结构信息的相似性方法(CN、HDI、PA)、基于路径的相似性方法(LP、Katz)和基于全局随机游走的相似性方法(ACT)。下面分别对其作简要介绍。

1)CN指标。若Γ(x)与Γ(y)分别表示节点x与节点y的直接邻居集合，那么基于CN指标的相似性可以表示为Sxy=|Γ(x)∩Γ(y)|。

2)HDI指标：

Sxy=|Γ(x)∩Γ(y)|/ max {kx,ky}

其中kx与ky分别表示节点x与节点y的度。在这一指标中分母由度较高的节点决定，其意在减弱度值高的节点对相似性的影响。

3)PA指标。它是一个只考虑节点度相似性的指标。在无标度网络中，一条新边连接到节点x的概率正比于节点的度kx。其定义为Sxy=kxky。

4)LP指标。它是在CN的基础上考虑了三阶路径的影响，定义为S=A2+αA3。其中α为可调节参数，用来控制三阶路径的影响；A表示网络的邻接矩阵。

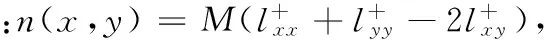
3.5 实验结果

将本文提出的算法DWRWR和DWLRW在3.1节中的5个数据集上进行实验，为了更加准确呈现预测结果，在所有数据集上重复独立实验100次，并计算这100次实验的AUC平均值作为最后的预测结果。表2列出了各算法在5个数据集上预测结果的AUC值比较；表3列出了所提算法DWRWR和DWLRW的AUC指标相对于RWR和LRW算法在5个数据集上的改进程度。

从表2中可以看出，在5个数据集上，本文算法DWRWR和DWLRW分别比RWR和LRW算法在AUC指标上均有所提高，同时相较于各链路预测基准算法，其AUC值是最高的。从表3中可以看出，在5个数据集上，DWRWR算法相较RWR算法，其预测精确度平均提升了1.34%，DWLRW算法相较LRW算法，其预测精确度平均提升了0.34%。

因此，上述结果分析表明，通过DeepWalk学习各节点在潜在网络结构上的相似性，将其应用于RWR和LRW的转移过程中，在提升链路预测的精确度方面起到了积极作用。

表2 各算法在5个数据集上的预测AUC值比较Tab. 2 Comparison of AUC of each algorithm on five datasets

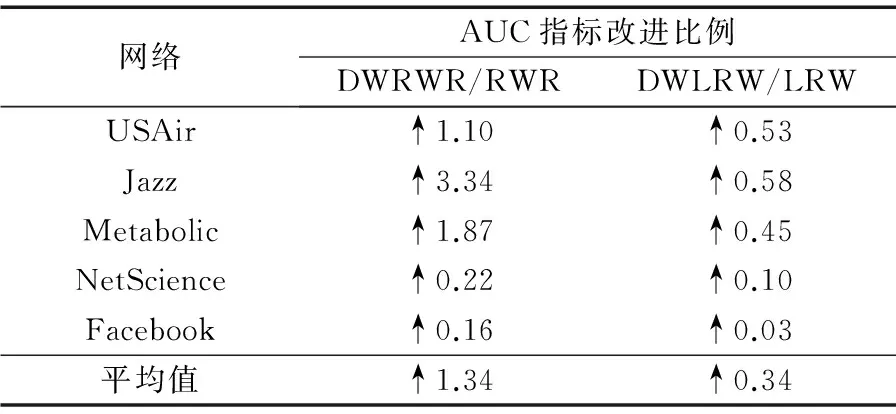
表3 算法的AUC指标改进比例 %Tab. 3 Improvement proportion of algorithm’s AUC %

4 结语

本文针对现有的基于随机游走的链路预测指标在无权网络中的转移过程存在较强随机性的问题，提出了一种基于网络表示学习与随机游走的链路预测算法。首先通过网络表示学习模型DeepWalk学习网络结构潜在特征，得到节点的低维向量表示；然后，将节点间的向量的相似性融合到LRW和RWR的随机游走转移过程中，重新定义出不同邻居节点间的转移概率，使其在转移过程中考虑了邻居节点在网络结构上的相似性。实验结果表明，本文所提算法DWRWR和DWLRW对比现有众多链路预测算法有着更加准确的预测结果。在下一步的研究中，可以尝试考虑一种同时结合网络结构和节点属性信息的网络表示学习方法在链路预测问题上的应用。

References)

[1] 吕琳媛.复杂网络链路预测[J].电子科技大学学报,2010,39(5):651-661.(LYU L Y. Link prediction on complex networks [J]. Journal of University of Electronic Science and Technology, 2010, 39(5): 651- 661.)

[2] 胡文斌,彭超,梁欢乐,等.基于链路预测的社会网络事件检测方法[J].软件学报,2015,26(9):2239-2355.(HU W B, PENG C, LIANG H L, et al. Event detection method based on link prediction for social network evolution [J]. Journal of Software, 2015, 26(9): 2339-2355.)

[3] LU L Y, ZHOU T. Link prediction in complex networks: a survey [J]. Physica A: Statistical Mechanics and Its Applications, 2011, 390(6): 1150-1170.

[4] JACCARD P. Étude comparative de la distribution florale dans uneportion des Alpes et des Jura [J]. Bulletin del la Société Vaudoise des Sciences Naturelles, 1901, 37: 547-579.

[5] ADAMIC L A, ADAR E. Friends and neighbors on the Web [J]. Social Networks, 2003, 25(3): 211-230.

[6] BARABASI A L, ALBERT R. Emergence of scaling in random networks [J]. Science, 1999, 286(5439): 509-512.

[7] ZHOU T, LU L Y, ZHANG Y C. Predicting missing links via local information [J]. The European Physical Journal Condensed Matter and Complex System, 2009, 71(4): 623-630.

[8] LU L Y, JIN C H, ZHOU T, Similarity index based on local paths for link prediction of complex networks [J]. Physical Review E, 2009, 80(4): 046122.

[9] KATZ L. A new status index derived from sociometric analysis [J]. Psychometrika, 1953, 18(1): 39-43.

[10] LEICHT E A, HOLME P, NEWMAN M E J. Vertex similarity in networks [J]. Physical Review E, 2006, 73(2): 026120.

[11] KLEIN D J, RANDIC M. Resistance distance [J]. Journal of Mathematical Chemistry, 1993, 12(1): 81-95.

[12] TONG H, FALOUTSOS C, PAN J Y. Fast random walk with restart and its applications [C]// Proceedings of the 6th International Conference on Data Mining. Piscataway, NJ: IEEE, 2006: 613-622.

[13] LIU W P, LU L Y. Link prediction based on local random walk [J]. Europhysics Letters, 2010, 89(5): 58007.

[14] CHERRY A, ABBER E. Enhancing link prediction in twitter using semantic user attribute [C]// Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. New York: ACM, 2015: 1155-1161.

[15] 陈维政,张岩,李晓明.网络表示学习[J].大数据,2015,1(3): 8-22.(CHEN W Z, ZHANG Y, LI X M. Network representation learning [J]. Big Data Research, 2015, 1(3): 8-22.)

[16] 孙志远,鲁成祥,史忠植,等.深度学习研究与进展[J].计算机科学,2016,43(2):1-8.(SUN Z Y, LU C X, SHI Z Z, et al. Research and advances on deep learning [J]. Computer Science, 2016, 43(2): 1-8.)

[17] MIKOLOV T, SUTSKEVER I, CHEN K, et al. Distributed representations of words and phrases and their compositionality [C]// NIPS’13: Proceedings of the 26th International Conference on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2013: 3111-3119.

[18] PEROZZI B, AL-RFOU R, SKIENA S. DeepWalk: online learning of social representations [C]// Proceedings of the 20th ACM SIGKDD International Conference On Knowledge Discovery and Data Mining. New York: ACM, 2014: 701-710.

[19] BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine [J]. Computer Networks and ISDN Systems, 1998, 30(1): 107-117.

[20] YOSHUA B, REJEAN D, PASCAL V, et al. A neural probabilistic language model [J]. Journal of Machine Learning Research, 2003, 3(6): 1137-1155.

[21] MORIN F, BENGIO Y. Hierarchical probabilistic neural network language model [C]// Proceedings of the 10th International Workshop Conference on Artificial Intelligence and Statistics. Cambridge, CA: MIT Press, 2005: 246-252.

[22] HANLEY J A, MCNEIL B J. The meaning and use of the area under a Receiver Operating Characteristic (ROC) curve [J]. Radiology, 1982, 143(1): 29-36.

This work is partially supported by the Natural Science Foundation of Guangdong Province (2016A030313441), the Science and Technology Planning Project of Guangdong Province (2015B010129009, 2016A030303058, 2016A090922008, 2015A020209178), the Open Project Program of Guangdong Provincial Key Laboratory of High Performance Computing (T191527), the Science and Technology Program of Guangzhou (201604016035).

LIUSi, born in 1992, M. S. candidate. His research interests include data mining, big data processing.

LIUHai, born in 1974, Ph. D., associate professor. His research interests include text mining, deep learning.

CHENQimai, born in 1965, M. S., professor. His research interests include data mining, machine learning.

HEChaobo, born in 1981, Ph. D., associate professor. His research interests include data mining, social computing.

Linkpredictionalgorithmbasedonnetworkrepresentationlearningandrandomwalk

LIU Si1, LIU Hai1,2*, CHEN Qimai1, HE Chaobo3

(1.SchoolofComputer,SouthChinaNormalUniversity,GuangzhouGuangdong510631,China；2.GuangdongProvincialKeyLaboratoryofHighPerformanceComputing,GuangzhouGuangdong510033,China；3.SchoolofInformationScienceandTechnology,ZhongkaiUniversityofAgricultureandEngineering,GuangzhouGuangdong510225,China)

The transition process of existing link prediction indexes based on random walk exists strong randomness in the unweighted network and does not consider the effect of the similarity of the network structure between different neighbor nodes on transition probability. In order to solve the problems, a new link prediction algorithm based on network representation learning and random walk was proposed. Firstly, the latent structure features of network node were learnt by DeepWalk which is a network representation learning algorithm based on deep learning, and the network nodes were encoded into low-dimensional vector space. Secondly, the similarity between neighbor nodes in vector space was incorporated into the transition process of Random Walk with Restart (RWR) and Local Random Walk (LRW) respectively and the transition probability of each random walk was redefined. Finally, a large number of experiments on five real datasets were carried out. The experimental results show that the AUC (Area Under the receiver operating characteristic Curve) values of the proposed algorithms are improved up to 3.34% compared with eight representative link prediction benchmarks based on network structure.

link prediction; similarity; Random Walk with Restart (RWR); Local Random Walk (LRW); network representation learning

TP391; TP18

A

2016- 12- 29;

2017- 02- 09。

广东省自然科学基金自由申请项目(2016A030313441)；广东省科技计划项目(2015B010129009, 2016A030303058, 2016A090922008, 2015A020209178)；广东省高性能计算重点实验室开放课题项目(T191527)；广州市科技计划项目(201604016035)。

刘思(1992—)，男，江西丰城人，硕士研究生，CCF会员，主要研究方向：数据挖掘、大数据处理； 刘海(1974—)，男，湖南张家界人，副教授，博士，CCF会员，主要研究方向：文本挖掘、深度学习； 陈启买(1965—)，男，湖南衡阳人，教授，硕士，主要研究方向：数据挖掘、机器学习； 贺超波(1981—)，男，广东河源人，副教授，博士，CCF高级会员，主要研究方向：数据挖掘、社会计算。

1001- 9081(2017)08- 2234- 06

10.11772/j.issn.1001- 9081.2017.08.2234