基于可传递性的公平的外包计算协议

李海颖,张江霄,隋春荣

(邢台学院 数学与信息技术学院，河北 邢台 054001)

基于可传递性的公平的外包计算协议

李海颖,张江霄,隋春荣

(邢台学院 数学与信息技术学院，河北 邢台 054001)

针对现有的外包计算存在外包计算不公平性、用户和外包者不是匿名的、且用户无法传递外包计算的问题，基于可传递条件模型，构建了一个公平的用户和外包者匿名的可传递外包计算协议.利用Groth-Sahai的承诺和对应证明的可自更新性，新协议保证了用户和外包者的匿名性，且允许用户在不想进行计算时，可以不通过外包者，直接把该计算传递给其他用户，从而增加了外包计算的实用性.

外包计算；匿名性；GS证明；交互签名；可传递性条件

外包计算允许某个需要做大量计算任务的用户，把自己的工作交给云中的一个外包者OU，OU然后可以把任务外包给很多其他的用户W，在W完成所分配的任务后，OU再付给W对应的报酬.也正是外包计算的出现，既可以帮助某些用户完成计算量很大的任务，也可以充分利用某些闲置的用户.但是外包计算存在外包者和用户之间的不公平问题，即：无法保证外包者付费给用户后，用户却没有按量完成所分配的计算量；无法保证用户在完成所分配的计算量后，外包者却不支付所对应的费用；外包者和用户之间无法保证公平的交换，同时外包者和用户不具有匿名性.

正是外包计算的众多优点，很多学者对其进行研究.为了解决外包者和用户之间的不公平问题，Golle等[1]首先引入环模式，利用环模式的限制，OU能够以很大的概率确定W已经足量的完成了OU所分配的任务；Carbunar[2]提出了一个基于公平条件付费的外包计算，解决了在用户完成所分配的计算量后，却无法收到对应的费用问题，但是他使用了切割选择算法和秘密分享协议，因此协议的效率很低；Carbunar[3]又提出了一个新的基于公平付费的外包计算协议，利用的基本协议是条件电子现金协议[4]和可传递电子现金协议[5]，但是该协议仍然使用了切割选择算法，因此协议的效率仍然很低.在2012年，Chen等[6]基于公平的条件付费协议，使用验证加密构建了一个外包计算协议，该协议考虑了懒惰的、部分诚实的用户，但是该协议的OU和W都不是匿名的，而且当外包者的外包任务很多的情况下，外包者的计算量太大.Guillevic[7]和Ma[8]等分别针对特殊函数、一般函数等的专项计算量问题的外包问题研究.2016年，任艳丽等[9]提出基于单个双线性对运算的可完全验证的外包算法，提高了用户的可验证概率.李福祥等[10]针对外包计算只有计算委托方才可以对结果验证的问题，构建了一个基于双线性映射的公共可验证外包计算方案；2017年，韩益亮等[11]将属性签名与外包双线性对计算相结合，提出了一个外包计算结果可验证的辅助验证属性签名方案.陈振华等[12]设计了内积协议，基于此协议构建了一个云外包计算中空间位置关系的保密判断.张维纬等[13]构建了一个支持安全外包计算的无线体域网数据共享方案.

针对已有的外包模型中，存在外包计算的不公平性、OU和W不是匿名的，以及外包者任务繁重的问题，构建了一个OU、W1和相应的传递者Wi都是匿名的公平的外包计算协议，且在某个W1不想做自己的外包任务时，无需让OU重新分配任务，就可以直接把自己的外包任务传递给另一个用户W2，同时能保证W1、W2和OU的匿名性.

1 背景知识及可传递条件模型

1.1 基础知识

为了能更好地构建基于可传递性的公平的外包计算协议，本节给出所使用的密码学原语.

定义1(双线性对)双线性对是一个满足下面条件的映射，定义ê：G1×G2→G3，其中群G1、G2和G3是阶乘法循环群，p为素数；g,h分别是群G1和G2的生成元.

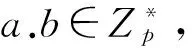
2)(非退化性)ê(g.h)≠1；

3)(可计算性)ê是多项式时间可计算的.

定义2(SXDH问题)[14]设(p,G1,G2,G3,ê,g,h)是一个素数阶群，其中p为素数，g,h分别是G1,G2的生成元，ê：G1×G2→G3.SXDH(Symmetric external Diffe-Hellman)问题指在群G1和G2上DDH问题是困难的.

定义3(GS证明) GS证明[14]在标准模型下给出有关双线性群中等式的非交互式零知识证明，它适合多种双线性群中群元素关系的等式，具体包括：双线性乘积等式、多标量乘法等式和二次等式，本文只使用基于SXDH假设下的双线性乘积等式.

定义4(交互签名) 交互签名[15]允许用户对消息、验证秘钥、对应的签名做承诺，并证明被承诺的签名是被承诺消息的签名.交互签名提供了很多算法，本文只需要算法SigCom，具体算法如下：

在密钥sk给出一个消息M的承诺CM，算法SigCom允许签名者可以在密钥sk下直接生成消息M的签名σ的承诺Cσ以及对应的证明πσ，该证明证明了Cσ是一个消息承诺CM的一个有效的签名，同时签名者又不知道消息承诺CM的原消息M.在此消息M是Diffe-Hellman对(x,y)∈G1×G2，具体是指存在一个a∈Zp，且x=ga,y=ha.

1.2 可传递条件模型

可传递条件模型首先在文献[16]中提出，该模型允许用户从商家购买商品，向商家支付对应面额的电子现金，商家在收到用户支付的电子现金后，无需存入银行就可以直接花费该电子现金，直到某个商家不想花费该电子现金，而是存入银行，同时用户和商家在花费之前，会附加一个条件，该条件在满足某个触发条件时，可以对电子现金的流向进行调整，从而满足某个已知条件.该模型可以用于在线赌博、预言市场等应用.本文就是利用该模型来解决外包计算的公平性问题，既允许用户自己完成外包计算，也可以把该外包计算传递给其他用户，当存在下面条件：用户的计算不完整或者商家没有给用户付对应的报酬时，就可以利用此模型中的条件性来达到外包计算的公平性.具体参见图1.

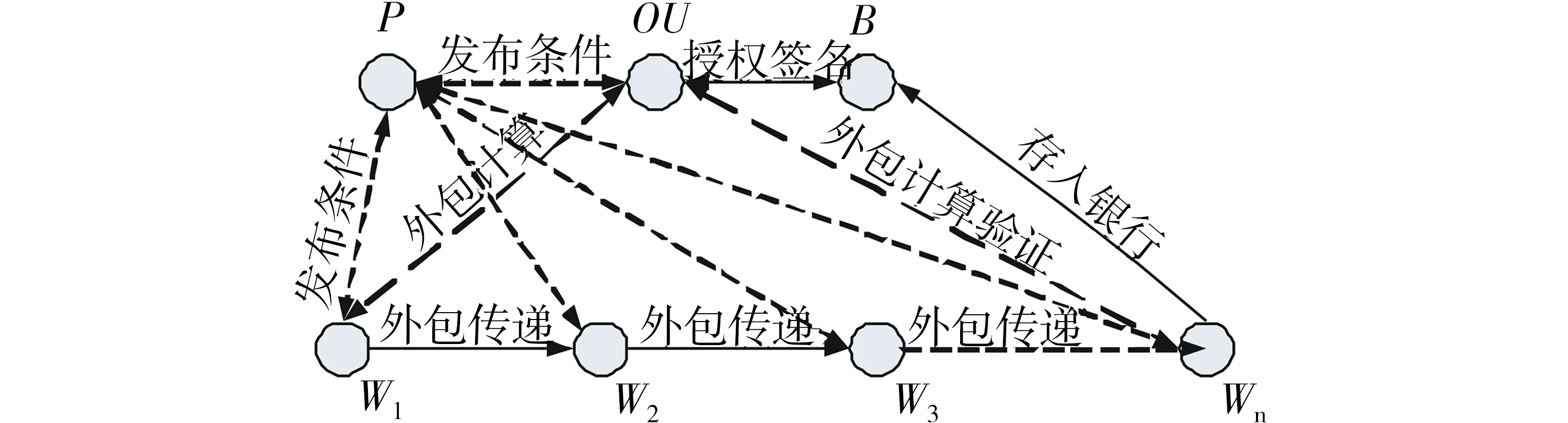
图1 可传递条件模型Fig.1 Transferable and conditional model

2 匿名的可传递外包计算协议

可传递条件模型保证用户正常完成计算并获得对应的报酬，或者用户直接把该计算传递给其他用户，其他用户完成计算后再获得相应的报酬，当外包者收到计算结果后，会进行简单判断就给用户支付对应的报酬，但是如果在后面固定时间内发现计算结果不正确，就会给条件者发送错误信息，这样就导致用户无法获得对应的条件承诺值，用户也就无法从银行提取对应的电子现金面额；同样若用户计算结果正确，并未获得相应的计算报酬，用户也会向条件者发送外包者的错误信息，也就导致外包者会得到银行对应的惩罚.从而实现匿名的公平的可传递外包计算协议.匿名的可传递外包计算由外包者OU、多个用户W1、W2、…、Wn、条件者P和银行B组成.

2.1 基本参数

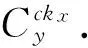
2.2 所需算法

本文所构造的匿名的可传递外包计算协议主要需要以下2个算法.

Verify(OU(params,pkOU,skou,ckB,result)↔P(ckP,ekP)：此协议是一个交互协议，OU验证用户所提供的结果result是否正确，若正确就给P发送用户计算正确的消息，以便后期用户从P得到被承诺的值；若计算结果不正确，则给P发送用户计算错误的消息，以及Wi的计算结果和对应的错误证明，综合判定结果，以便OU赎回自己的电子现金；

Redeem(W(params,pki,ski,biao)P(ckP,ekP))：此协议是一个交互协议，若W收到OU的电子现金，且P收到OU发送的用户计算正确的消息，P就给W解开被承诺值，以便W能从银行提取对应的电子现金；若W进行正确计算后，P没有收到OU发送的用户计算正确的消息，则向P提供计算的结果和对应的正确证明，综合判定后，P再给W解开被承诺值，以便W能从银行提取对应的电子现金.

2.3 生成协议

包括条件生成和签名生成，具体描述如下.

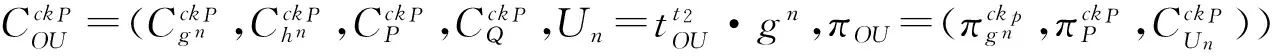
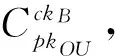
2.4 计算协议

此协议或者允许用户完成相应的计算任务，或者允许用户把该计算任务转移给其他人，从而能实现计算任务的直接转移，减轻OU的负担.具体协议如下：

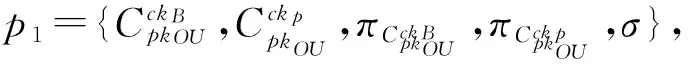
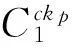
2.5 付费协议

此协议允许OU验证用户提供的计算结果result的正确性，若正确，则OU给P发送用户计算正确的消息，以便帮助用户能从银行提取自己的报酬.若不正确，则OU给P发送用户计算错误的消息，并提供错误的计算结果以及对应的证明，在P验证成功后，再允许OU赎回自己的电子现金.具体协议如下：

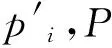
3 安全属性分析

本文所构造的匿名的可传递外包计算协议具有正确性、公平性、不可重复花费性、可传递性和传递凭条的不可链接性.下面分别进行简要的说明.

说明1：本协议具有正确性.如果外包者和用户都是诚实的，他们将在付费协议中执行交换协议，并最终能保证用户可以得到相应的报酬，而外包者能得到正确的计算结果.

说明2：本协议具有公平性.首先外包者可以得到完整的计算结果，假设扮作攻击者的用户，获得了相应的凭条，但是外包者没有得到相应的计算结果.如果攻击者能实现这个，却没有给外包者相应的计算结果，那攻击者只有从条件者处获得相应的凭条，即条件者获得了相应计算结果，那外包者也会从条件者处获得相应的计算结果，这和前提条件矛盾，因此对于外包者来说是公平的，即外包者可以获得完整的计算结果.

说明3：本协议具有匿名性[16].本协议中W1,W2和OU具有匿名性.

其次W1具有匿名性，W1在自己完成计算时，会给条件者提供对应的承诺值和错误信息，在提供之前，都需要利用GS证明的可自更新性，对承诺值和错误信息进行更新，但是由GS证明可自更新性的不可区分性，可知，W1具有匿名性；当W1把计算传递给W2后，同时给W2提供对应的承诺值，在提供之前W1仍然利用GS证明的可自更新性，对承诺值进行更新，这样就保证了W1的匿名性.总之，W1具有匿名性.以此类推，W2也具有匿名性.

说明4：本协议外包者具有不可重复花费性[16].假设外包者把相同的电子现金付给了不同的用户，有以下2种可能：第一，外包者向不同的用户提供了相同的凭条，这在后期会被银行发现；第二，外包者向不同的用户支付了不同的凭条，那说明外包者可以成功地伪造银行的签名，但是交互签名是无法伪造的，因此这也是不可能的，因此本协议中外包者不可能发生重复花费.

说明5：本协议中传递用户之间的凭条具有不可链接性[16].假设本协议是可链接的，则攻击者必须能够区分原承诺和更新后的承诺，由于GS证明中承诺的更新是不可区分的.因此，本协议中传递用户之间的凭条具有不可链接性.

4 效率分析

把本文、Carbunar[2]和Chen[6]等构建的协议分别从外包者单位时间的计算量、外包计算协议的公平性和匿名性3部分进行比较，具体的比较结果见表1.

表1 外包计算协议的计算量和安全属性比较Tab.1 Efficiency and security properties comparison in outsourcing computations scheme

由表1可以知道新的外包计算协议，由于可传递条件模型的特性，可以允许外包者有一定的弹性验证时间，而且可以利用条件性对报酬的流向进行调整，使得新协议中外包者单位时间的计算量不大，允许外包者可以处理很重的计算任务；也是因为可传递条件模型使得新协议具有公平性；由于GS证明的可自更新性保证了外包者和用户的匿名性.因此，新协议的效率更高，更实用.

5 结束语

本文构建了一个用户和外包者的身份是匿名的，且用户在不想完成计算时，可以实现外包计算可传递性的公平外包计算协议.基于可传递条件模型，保证了外包计算协议的公平性；利用GS证明的可更新性，保证了用户和外包者身份的匿名性.同时，在保证用户和外包者匿名性的前提下，减少了外包者单位时间的计算量.因此本协议的效率更高，实用性更强.

[1] GOLLE P,MIRONOV I.Uncheatable distributed computations[C]∥ CT-RSA 2001.Topics in Cryptiology-CT-RSA 2001,LNCS 2020,Berlin,German: Springer,2001:425-440.

[2] CARBUNAR B,TRIPUNITARA M.Conditional payments for computing markets[C]∥ CANS 2008.Cryptology and Network Security,LNCS 5339,Berlin,German: Springer,2008:317-331.

[3] CARBUNAR B,TRIPUNITARA M.Fair payments for outsourced computations[Z].IEEE Communications Society Conference on Sensor,Mesh and Ad Hoc Communications and Networks,Boston,Massachusetts,USA，Piscataway,2010.

[4] SHI L,CARBUNAR B,SION R.Conditional e-Cash[C]∥ FC 2007.Financial Cryptography and Data Security,LNCS 4886,Berlin,German: Springer,2007:15-28.

[5] 张江霄,李舟军,高延武,等.基于花费链最优匿名的等长可传递电子现金系统[J].电子学报,43(9),1805-1809,2015.DOI: 10.3969/j.issn.0372-2112.2015.09.019.

ZHANG J X,L I Z J,GAO Y W,et al.Transferable e-cash system of equal length with optimal anonymity based on spending chain[J].Acta Electronica Sinica,43(9),1805-1809,2015.DOI: 10.3969/j.issn.0372-2112.2015.09.019.

[6] CHEN X F,LI J,SUSILO W.Efficient fair conditional payments for outsourcing computations[J].IEEE Transactions on Information Forensics and Security,2012,7(6):1687-1694.DOI:10.1109/TIFS.2012.2210880.

[7] GUILLEVIC A,VEGNAUD D.Algorithms for outsourcing pairing computation[C]∥ CARDIS 2014.Smart Card Research and Advanced Applications,LNCS 8968,Berlin,German: Springer,2015: 193-211.

[8] MA X,LI J,ZHANG F G.Outsourcing computation of modular exponentiations in cloud computing[J].In Cluster Compute,2013,16(4):787-796.DOI:10.1007/s10586-013-0252-0.

[9] 任艳丽,丁宁,王天银,等.可完全验证的双线性对运算外包算法[J].中国科学：信息科学，2016,46:855-869.DOI: 10.1360/N112016-00020.

REN Y L,DING N,WANG T Y,et al.New algorithms for verifiable outsourcing of bilinear pairings[J].Scientia Sinica Informationis,2016,46:855-869.DOI: 10.1360/N112016-00020.

[10] 李福祥,霍建秋,林慕清,等.基于双线性映射的公共可验证外包计算方案[J].东北大学学报(自然科学版),2016,37(5)：619-623.DOI:1005-3026(2016)05-0619-05.

LI F X,HUO J Q,LIN M Q,et al.Bilinear map-based public verifiable outsourced computation scheme[J].Journal of Northeastern University (Natural Science),2016,37(5):619-623.DOI:1005-3026(2016)05-0619-05.

[11] 韩益亮,陈飞,杨晓元.可验证的外包属性签名方案[J].密码学报,2017,4(2):151-164.DOI: 10.13868/j.cnki.jcr.000170.

HAN Y L,CHEN F,YANG X Y.Verifiable outsourcing attribute-based signature scheme[J].Journal of Cryptologic Research,2017,4(2):151-164.DOI: 10.13868/j.cnki.jcr.000170.

[12] 陈振华,李顺东,黄琼,等.云外包计算中空间位置关系的保密判断[J].计算机学报,2017,40(2):351-363.DOI: 10.11897/SP.J.1016.2017.00351.

CHEN Z H,LI S D,HUANG Q,et al.Privacy-preserving determination of spatial location-relation in cloud computing[J].Chinese Journal of Computers,2017,40(2):351-363.DOI: 10.11897/SP.J.1016.2017.00351.

[13] 张维纬,张育钊,黄焯,等.支持安全外包计算的无线体域网数据共享方案[J].通信学报,2017,38(4):64-75.DOI: 10.11959/j.issn.1000-436x.2017085.

ZHANG W W,ZHANG Y Z,HUANG C,et al.Data sharing scheme supporting secure outsourced computation in wireless body area network[J].Journal on Communications,2017,38(4):64-75.DOI: 10.11959/j.issn.1000-436x.2017085.

[14] GROTH J,SAHAI A.Efficient Non-interactive proof systems for bilinear groups[C]∥ In EUROCRYPT 2008.Advances in Cryptology-EUROCRYPT 2008,LNCS 4968,Berlin,German: Springer,2008:415-432.

[15] FUCHSBAUER G.Commuting signatures and verifiable encryption[C]∥ CRYPTO 2011.Advances in Cryptology-EUROCRYPT 2011,LNCS 6632,Berlin,German: Springer,2011:224-245.

[16] ZHANG J X,GUO H,LI Z J,et al.Transferable conditional e-cash with optimal anonymity in the standard model[J].IET Information Security,2015，9(1): 59-72.DOI:10.1049/iet-ifs.2013.0138.

(责任编辑：孟素兰)

Fairoutsourcingcomputationsschemebasedontransferability

LIHaiying，ZHANGJiangxiao，SUIChunrong

(Mathematics and Information Technology Institute，Xingtai University，Xingtai 054001，China)

In outsourcing computations,there exist some problems such as the unfairness of outsourcing computations,the user and outsourcer is not anonymous,and the non-transferable of the outsourcing computations.This paper proposed a fair,full anonymous and transferable outsourcing computations scheme based on the transferable and conditional model.Using the Groth-Sahai's self-updating of commitment and corresponding proving,the new scheme guarantees that the user and outsourcers are fully anonymous.When the user didn't want to do the computation,he can transfer the computations to another.At last,these would improve the practicability of the outsourcing computations.

outsourcing computations;anonymity;GS proof;commuting signature;transferability and condition

TP309

A

1000-1565(2017)05-0555-06

10.3969/j.issn.1000-1565.2017.05.016

2017-03-22

河北省社科基金资助项目(HB14TQ005)

李海颖(1976—)，女，河北邢台人，邢台学院副教授，主要从事云计算方面研究.E-mail：rmth11@163.com

张江霄(1983—)，男，河北邢台人，邢台学院讲师，博士.主要从事云计算及大数据方向研究.E-mail：orange_0092008@163.com