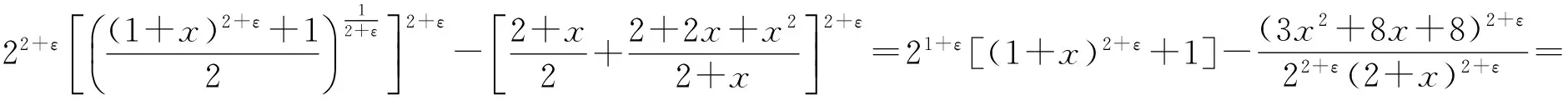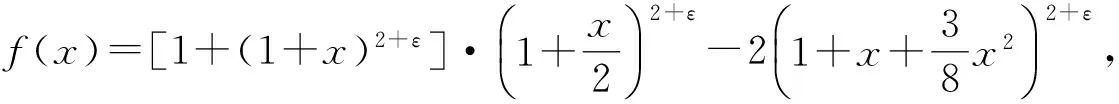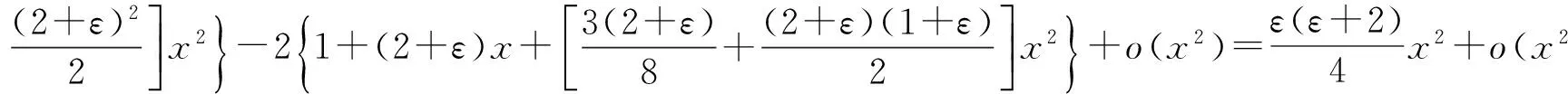幂平均的凸组合界
2017-10-19孟祥菊田淑环许会峰
孟祥菊,田淑环,许会峰
(保定学院 数学与计算机系,河北 保定 071000)
幂平均的凸组合界
孟祥菊,田淑环,许会峰
(保定学院 数学与计算机系,河北 保定 071000)
得到了关于几何平均G(a,b)、反调和平均C(a,b)、幂平均Mr(a,b)和算术平均A(a,b)的不等式,对所有的a、b>0成立的γ的最佳值.
幂平均;几何平均;反调和平均;算术平均

1995年,Seiffert[1]证明了不等式M1(a,b)
StoLarsky[2]证明了不等式I(a,b)=L0(a,b)≥M2/3(a,b),当且仅当a=b时等号成立.
褚玉明等[3]证明了不等式αT(a,b)+(1-α)G(a,b)
经典平均在物理学、天文学、气象学中有广泛的应用,它们之间的估计式是近年来研究的热门课题.国内外学者们[4-9]建立了一系列精确的不等式,这些结果是经典结论的推广和发展.
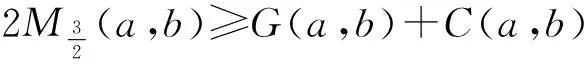
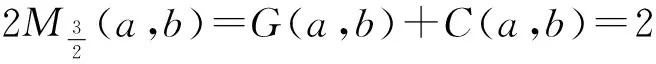
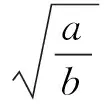
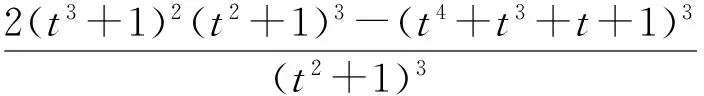

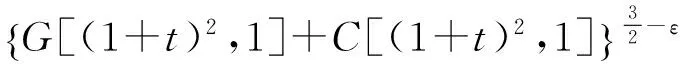
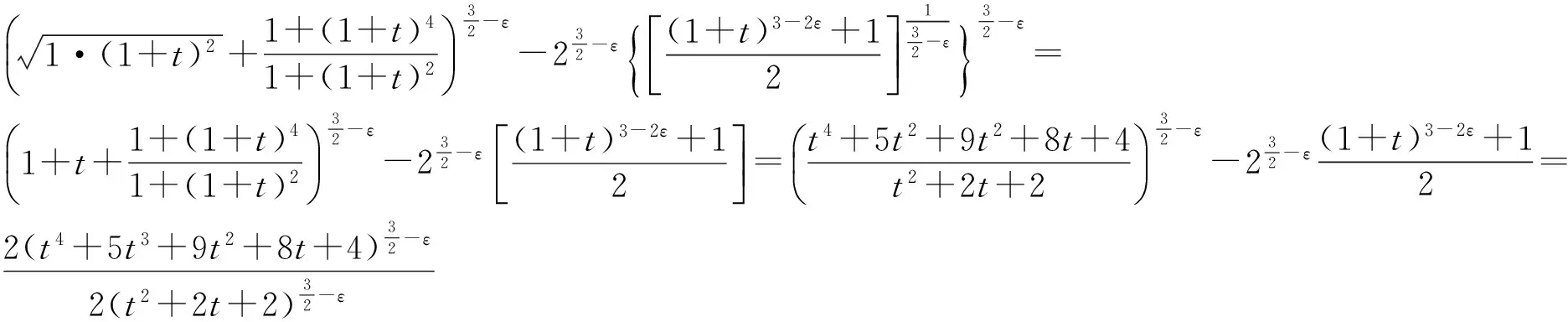
(1)
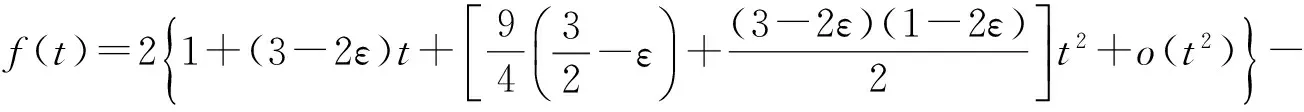
(2)
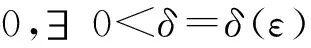
定理2不等式A(a+b)+C(a+b)≥2M2(a,b)当且仅当a=b时等号成立.
证明若a=b,则A(a,b)+C(a,b)=2M2(a,b)=2a.



故A(a,b)+C(a,b)≥2M2(a,b)
下面证明2M2(a,b)是幂平均关于算术平均和反调和平均的最佳凸组合下界.
对于∀ε>0,0 (3) (4) [1] SEIFFERT H J.Aufgabe 16[J].Die Wurzel,1995,29(87):221-222. [2] STOLARSKY K B.The power and generalized logarithmic means[J].The American Mathematical Monthly,1980,87(7):545-548. [3] CHU Y M,ZONG C,WANG G D.Optimal convex combination bounds of Seiffert and geometric means for the arithmetic mean[J].J Math Inequal,2011,5(3):429-434. [4] RICHARDS K C.Sharp power mean bounds for the Gaussian hypergeometric function[J].Journal of Mathematical Analysis and Applications,2005,3089(1):303-313. [5] CHU Y M,WANG M K,WANG G D.The optimal generalized logarithmic Mean boundcs for seiffert’s mean[J].Acta Mathematica Scientia,2012,32B(4):1619-1626. [6] 孟祥菊,潘学功,高梦涵.对数平均的最优凸组合界[J].河北大学学报(自然科学版),2014,34(5):471-474.DOI:10.3969/j.issn.1000-1565.2014.05.005 MENG X J,PAN X G,GAO M H.Optimal convex combination bounds for logarithmic mean[J].Journal of Hebei University(Natural Science Edition),2014,34(5):471-474.DOI:10.3969/j.issn.1000-1565.2014.05.005 [7] 赵铁洪,褚玉明.对数平均和双参数广义Muirhead平均之间的比较[J].中国科学:数学,2015,45(3):233-244. ZHAO T H,CHU Y M.Comparison between the logarithmic and two-parameter generalized Muirhead means[J].Science China(mathematics),2015,45(3):233-244. [8] 史明宇,褚玉明,蒋月评.关于幂平均、调和平均和指数平均的最佳不等式[J].数学物理学报,2011,31A(5):1377-1384. SHI M Y,CHU Y M,JIANG Y P.Optimal inequalities related to the power,harmonic and identric means[J].Acta Mathematica Scientia,2011,31A(5):1377-1384. [9] 孙惠,褚玉明.Toader平均的二次与调和平均界[J].数学物理学报,2015,35A(1):36-42. SUN H,CHU Y M.Bounds for toader mean by quadratic and harmonic means[J].Acta Mathematica Scientia,2015,35A(1):36-42. (责任编辑:王兰英) Optimalconvexcombinationboundsforthepowermean MENGXiangju,TIANShuhuan,XUHuifeng (Department of Mathematics and Computer Science,Baoding College,Baoding 071000,China) The optimal value of parameters are obtained to make the following double inequality holds for alla,b>0,2Mr(a,b)≥G(a,b)+C(a,b)andA(a,b)+C(a,b)≥2Mr(a,b)whereMr(a,b),G(a,b),C(a,b),A(a,b)denote the power mean,the geometric mean,the contraharmonic mean,the arithmetic mean of two different positive numbers a and b respectively. the power mean;the geometric mean;the contraharmonic mean;the arithmetic mean O178 A 1000-1565(2017)05-0454-03 10.3969/j.issn.1000-1565.2017.05.002 2016-11-25 河北省软科学基金资助项目(154576249);河北省自然科学基金资助项目(A2015201149) 孟祥菊(1971—),女,河北卢龙人,保定学院副教授,主要从事几何函数论的研究.E-mail:mengxiangju328@163.com