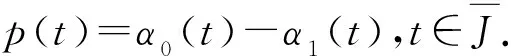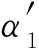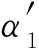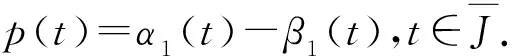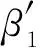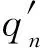一类二阶泛函微分方程初值问题解的收敛性

王培光，付芳芳，鲍俊艳

(河北大学 数学与信息科学学院，河北 保定 071002)

一类二阶泛函微分方程初值问题解的收敛性

王培光，付芳芳，鲍俊艳

(河北大学 数学与信息科学学院，河北 保定 071002)

利用拟线性化方法，讨论了Banach空间中一类二阶泛函微分方程初值问题解的收敛性，获得了解的平方收敛性结果.

Banach空间；泛函微分方程；拟线性化方法；平方收敛

在实Banach空间中讨论如下一类二阶泛函微分方程初值问题

(1)

这里φ∈C1=C([-r,0],E),f(t,xt,x′(t))∈C(J×C1×E,E),xt=x(t+τ),-r≤τ≤0.

拟线性化方法是研究各类微分方程解的收敛性的一种有力工具.与单调迭代方法相比较[1-2]，拟线性化方法可以得到解的平方收敛以及高阶收敛结果.已有学者将拟线性化方法应用到一阶与二阶泛函微分方程的讨论[3-5].本文在文献[6]的基础上，利用拟线性化方法对二阶泛函微分方程解的收敛性问题做进一步讨论.

1 预备知识

为方便后面的叙述和证明，首先给出如下概念和定义[7-9].

定义1若P是实Banach空间E中的非空凸闭集，并且满足1)x∈P，λ≥0⟹λx∈P；2)x∈P，-x∈P⟹x=θ，θ表示E中的零元素，则称P是E中的一个锥.

设P为实Banach空间E中的锥，则可在E中的元素间引入半序：任意x、y∈E，若y-x∈P，则x≤y.

定义2设{xn}单调递增且有上界，即存在y∈E，使得x1≤x2≤…≤xn≤…≤y.若存在x*∈E，使得‖xn-x*‖→0(n→∞)，则称锥P是正则的.

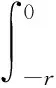
定义3设P是E中的正则锥，α(t)∈C*称为方程 (1)的下解，当且仅当

成立.若β(t)∈C*使得上述不等式反向成立，则称之为方程 (1)的上解.

引理1(Gronwall's不等式)假设u、α∈C[a,b]，非负函数β∈L1[a,b]，若

则

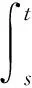
若进一步假设α(t)非减，则有

2 主要结果

设α0(t)、β0(t)∈C*使得在J上有α0(t)≤β0(t).定义集合

ω={(t,xt,x):α0(0)≤φ≤β0(0),α0(t)≤x(t)≤β0(t),t∈J}.

对于给定函数φ(t,xt,x)、ψ(t,xt,x)∈C1(ω,E)，使得φ(t,xt,x)≤ψ(t,xt,x).在(ω,E)上定义函数

其中Ω={(t,xt,x′)∶(t,xt,x)∈ω,φ(t,xt,x)≤x′≤ψ(t,xt,x)}.

考虑如下方程

(2)

有如下结果：

定理1设P为E中的正则锥，并且

H1)给定函数φ(t,xt,x)，ψ(t,xt,x)∈C1(ω,E)，满足φ(0,x0,x(0))≤x′(0)≤ψ(0,x0,x(0)).

H2)φ(t,xt,x),ψ(t,xt,x)的一阶Frechet导数存在，在ω上有

φt(t,xt,x)+φu(t,xt,x)φ(t,xt,x)+φv(t,xt,x)φ(t,xt,x)≤f(t,xt,x),

ψt(t,xt,x)+ψu(t,xt,x)ψ(t,xt,x)+ψv(t,xt,x)ψ(t,xt,x)≥f(t,xt,x).

证明设x(t)∈C*是方程 (2)的任一解，并且φ(0,x0,x(0))≤x′(0)≤ψ(0,x0,x(0)).下面用反证法证明φ(t,xt,x)≤x′(t)≤ψ(t,xt,x).假设存在一个t0∈[0,1]，使得x′(t0)>ψ(t0,xt0,x(t0)).定义函数

(3)

对式 (3)关于t求导，整理可得

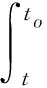
x″(t)-ψt(t,xt,x)-ψu(t,xt,x)x′(t+τ)-ψv(t,xt,x)x′(t)+ψu(t,xt,x)x′(t)+

ψv(t,xt,x)x′(t)-ψu(t,xt,x)ψ(t,xt,x)-ψv(t,xt,x)ψ(t,xt,x)≤

ψv(t,xt,x)ψ(t,xt,x)≤x″(t)-f(t,xt,ψ(t,xt,t))=θ.

因此有v′(t)≤θ.从而当0≤t≤t0时，有v(t0)≤v(t).又由v(t0)=x′(t0)-ψ(t0,xt0,x)>θ， 则有v(t)>θ.根据式(3)中v(t)定义，有v(0)≤θ，与v(t)>θ式矛盾.因此,x′(t)≤ψ(t,xt,x).同理可证φ(t,xt,x)≤x′(t).

综上可得φ(t,xt,x)≤x′(t)≤ψ(t,xt,x).定理证毕.

定理2设P为E中的正则锥，H3)成立，并且

H4)α0(t)、β0(t)∈C*分别为方程 (1)的下上解，并且α0(t)≤β0(t),t∈J.

H5)φ(t,γt,γ)≤γ′(t)≤ψ(t,γt,γ)，其中γ(t)=α0(t)或β0(t).对于α0(t)、β0(t)分别有

其中ψ(t,xt,x)关于xt、x是单调非增的.

H6)f(t,xt,x′)的一阶Frechet导数满足0

H7)f(t,xt,x′)的一阶Frechet导数满足Lipschitz条件，即存在常数Li,i=1,2,3,4 ，使得

|fu(t,xt,x′)-fu(t,yt,y′)|≤L1|xt-yt|+L2|x′-y′|，

|fv(t,xt,x′)-fv(t,yt,y′)|≤L3|xt-yt|+L4|x′-y′|.

则存在单调序列{αn(t)}、{βn(t)}一致且平方收敛于方程 (1)的解.

证明构造单调序列{αn(t)}、{βn(t)}如下:

下面用数学归纳法证明

α0≤α1…≤αn≤βn≤…≤β1≤β0，t∈J,

首先证明

(5)

由条件 H5)可得

即p″(t)≤θ，由此得到p(t)≤p(0)≤θ.

由条件H5)可得

综上所述，可得到式 (5).假设对于自然数n,有

(6)

即p″(t)≤θ，由此得到p(t)≤p(0)=θ.

其中f(t,xt,x′)≤N,N>0是常数.故必存在与n无关的δ，使得只要|t2-t1|<δ，就有

下证单调序列{αn(t)}、{βn(t)}平方收敛于方程(1)的解.

令

(7)

令

(8)

定义函数

(9)

因此单调序列{αn(t)}、{βn(t)}平方收敛于方程 (1)的解.定理证毕.

[1] BHASKAR T G，LAKSHMIKANTHAM V，DEVI J V.Monotone iterative technique for functional differential equations with retardation and anticipation[J].Nonlinear Analysis，2007，66(10)：2237-2242．

[2] WANG P G，WU H X，WU Y H.A note on monotone iterative technique for functional differential systems with retardation and anticipation[J].International Journal of Pure and Applied Mathematics，2007，41(5)：749-754．

[3] 王培光，高玮.集值微分方程初值问题的拟线性化方法[J].河北大学学报(自然科学版)，2011，31(1)：1-6.

WANG P G,GAO W.Quasilinearization of an initial value problem for set differential equations[J].Journal of Hebei University (Natural Science Edition)，2011，31(1)：1-6．

[4] JANKOWSKI T.Functional differential equations of second order[J].Bull Belg Math Soc，2003，10：291-298．

[5] 陈改平.具有滞后与超前的泛函微分方程的拟线性化方法[D].保定：河北大学，2011．

CHEN G P.Qvasilinearliation method for a class of funetional differential systems with retardation and anticijation[D].Baoding:Hebei university，2011.

[6] LE H H，LE T P N.Boundary and initial value problems for second-order neutral functional differential equations[J].Electronic Journal of Differential Equations，2006,62：1-19．

[7] 郭大钧.非线性泛函分析[M].北京：高等教育出版社，2015．

[8] LAKSHMIKANTHAM V，VATSALA A S.Generalized quasilinearization for nonlinear problems[M].Dordrecht：Kluwer Academic Publishers，1998．

[9] 张恭庆，林源渠.泛函分析讲义[M].北京：北京大学出版社，2014．

(责任编辑：王兰英)

Convergenceforaclassofsecond-orderfunctionaldifferentialequationswithinitialcondition

WANGPeiguang,FUFangfang,BAOJunyan

(College of Mathematics and Information Science,Hebei University,Baoding 071002,China)

The quasilinearization method is applied to discuss the convergence of the solutions for a class of second-order functional differential equations with initial condition in Banach space.We obtain the solutions for quadratic convergence of the approximate solutions.

Banach space;functional differential equations;quasilinearization;quadratic convergence

O175

A

1000-1565(2017)05-0449-05

10.3969/j.issn.1000-1565.2017.05.001