基于网络约束方法的交通事故空间点格局分析

聂 可，王振声，杜清运，张玉茜

（1. 深圳市数字城市工程研究中心，广东 深圳 518034；2. 国土资源部 城市土地资源监测与仿真重点实验室，广东 深圳 518034；3. 深圳大学 空间信息智能感知与服务深圳市重点实验室，广东 深圳 518060；4. 武汉大学 资源与环境科学学院，湖北 武汉 430079)

0 引 言

道路交通事故，直接影响到每个公民的出行安全，不仅对经济发展带来影响，而且危害社会和谐。道路交通事故是地理区域环境和人类在区域内活动共同作用的结果，近年来国内外学者对其展开了广泛关注，主要集中研究事故分布模式、事故成因分析[1]、事故预测及评估[2-3]，其中典型研究为事故黑点研究，如对黑点鉴别[4-5]、黑点评价[6]、黑点特征[2]等。关于交通事故的分布研究主要是从地理学视角观察道路交通事故聚集情况，采用空间格局分析方法揭示其空间分布规律，进而探测事故易发路段（或区域），从而使道路交通事故的管理和预防成为可能。大量研究表明交通事故的分布具有明显的空间聚集特性，即存在交通事故热区（也称黑区，即一组交通事故数高的连续路段形成的集合）[7]或交通事故热点[8](也称黑点，即事故数高的路口或单个路段)。然而，交通事故的发生位置是严格限定在道路网络上，是典型网络约束事件，根据Okabe等提出网络约束点事件分析思想[9-10]，认为传统的平面空间格局方法在分析网络点事件空间分布规律的弊端日益凸显，需要充分考虑道路网络的特性，采用网络约束空间点格局分析方法进行探讨。

近年来，随着GIS和几何计算的发展，对于网络约束点格局的发展逐渐有了进展[11-13]，并在交通事故的格局与形成过程的定量研究中得到了应用。网络约束点格局分析在机动车碰撞中的应用主要体现在机动车碰撞整体和局部格局分布探测，早期的交通事故研究中，学者们主要使用汇总数据将交通事故分散到道路路段上，对事故进行统计从而得到事故黑点[4,14]；随着汇总数据带来的可塑性单元面积问题，同时GIS技术对事故获取方法的改善，学者们尝试使用非汇总数据，即单条事故数据，对交通事故空间格局及形成过程进行定量化研究，其中广泛应用的方法是核密度估计方法[15-17]。核密度估计采用钟形密度函数进行交通事故点分布分析，被拓展到网络空间，即网络核密度估计，然而，网络核密度估计作为描述性分析方法，其估计结果缺少定量的统计检验[18-21]。因此，本文以武汉市交通事故展开研究，将核密度估计进行道路网络空间扩展，提出网络核密度估计方法探究交通事故的空间分布模式；并使用网络Moran's I方法对核密度估计结果进行统计显著性评价，揭示交通事故易发路段，以期为城市公共交通的健康发展提供科学参考。

1 研究区域与数据来源

1.1 研究区域

武汉市作为我国华中地区特大交通枢纽城市，随着城区的发展，市内交通日益成为一大问题，同时面临着较为严重的交通拥堵问题和较显著的交通事故危险。据武汉市交通管理局交通事故管理数据库不完全统计，2004～2008年5年间武汉市有记录交通事故为3309起、1976起、2676起、3113起、2499起。武汉市下辖江岸、江汉、硚口、汉阳、武昌、青山、洪山7个城区以及蔡甸、江夏、黄陂、新洲、东西湖、汉南6个远城区。由于2007年地铁轨道交通和三环尚未开通，交通出行主要发生在城市道路网络上，本文以2007年交通事故统计数据为例，有利于在考虑相对较少的事故影响因素的情况下，单纯讨论交通事故在路网空间下的地理分布模式。

1.2 数据来源及数据处理

交通事故是发生在道路上的人身伤亡或财产损失事件，其受发生场所即道路网络的约束，它属于二维平面的子空间的地理空间现象。本文旨在讨论交通事故在道路网络上的分布情况，主要涉及交通事故、武汉市路网数据、武汉市行政区划数据等。

交通事故数据主要由武汉市交通管理局提供，交通管理局采用数据库的方式对交通事故进行归档记录，主要记录事故基本信息、事故道路信息、事故处理信息三部分。由于本文不对交通事故的成因、伤亡情况、应急及改善方法进行研究，只提取交通事故的发生地址信息、发生时间、伤亡情况等信息。其中，交通事故的位置数据是采用传统的地址记载方式，如解放大道至武汉市药品检验所，本文采用百度地图的Geocoding API提供的地图服务进行地址匹配，以实现交通事故数据“落地”到武汉市地图上。武汉市交通路网数据来源于武汉市交通图（2007），武汉市行政区划数据来源于武汉市民政局。

2 研究方法

本文根据武汉市交通事故数据的特点，将交通事故分布现象抽象成点事件，点格局分析提供了区域上点位置空间布局的定量分析过程。核密度估计是空间离散点分析常用的方法，根据带宽的改变可以有效地刻画不同尺度上的空间聚类现象。由于交通事故是分布在路网空间下的点事件，采用平面核函数估计研究交通事故存在估计偏差，本文采用网络核密度估计方法揭示交通事故点的分布特点。

2.1 网络核密度估计方法

核密度估计方法是以聚集性为基础的基于密度分析的点模式分析方法，采用非参数的方法讨论空间数据的一阶属性。核密度估计方法通过计算每个要素在其周围邻域中的密度，并将相同位置处的密度进行叠加，得到整个区域的分布密度。平面空间点事件密度估计算子如下：

式中，λ(s)是位置点s的密度，r是核密度估计的搜索半径，只有在r内的点才能用来估算λ(s)距离s点dis的i点的权重。k为核密度估计中的核函数，是关于距离dis和半径r的比率函数，密度估计中充分考虑了距离衰减效应，中心位置处密度最大，随距离衰减，到极限距离处密度为0。

核函数的选择是核密度估计的第一步，核函数的类型有Gaussian、Quartic、Conic、Negative exponential、epanechnekov等。研究表明，在平面核密度估计中，核函数k影响小于搜索半径r[22]；r的选择决定了密度估计的光滑度，r越大密度图越光滑。

由于点集在路网上均匀分布，而在欧式平面上的密度却不是均匀的，分析由网络约束过程产生的点集，采用平面核密度估计方法会产生估计偏差，如图1所示。

图1 网络空间和平面空间中的点分布Fig. 1 Points distribution in network space and plane space

路网约束的网络核函数估计法和平面核函数估计方法有着相似的分析思路，两者的主要不同在于其距离量算方式的不同。网络核函数法以平面二维空间的函数方法为基础，为适应网状结构空间的需求，将距离量算方法从欧式距离扩展到网络距离，即网络中每个点到其他点的距离设定为最短网络路径距离，而非简单的欧式距离。网络空间点事件密度估计算子如下：

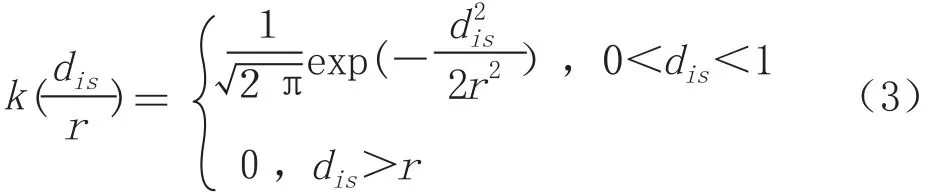
其核心思想在于将道路网空间分解为等长的线性单元记为lixel，然后用最短网络路径距离进行r值的量算。

2.2 网络Moran's I 统计

核密度估计作为描述性分析方法，由于其缺少定性的统计检验，主要用于得到直观的数据阐释图。本文对核密度估计结果进行局部Moran's I分析，对核密度估计结果进行统计检验，统计显著性的路段形成交通事故热点路段聚类。

假设交通事故在道路网的发生是完全随机分布的，那么路网上任何位置的事故发生率都等于总事故数与总路网长度的比值，即交通事故在定性和定量上都是完全均匀分布的。讨论空间过程时，可使用随机零假设或标准化零假设。本文在计算网络核密度估计值的网络局部Moran's I统计量时，采用99次条件空间排列模拟。条件空间排列模拟即不改变交通事故的数量，仅在原交通路段上改变交通事故的分布位置。网络约束Moran's I统计是建立在局部Moran's I和全局Moran's I的定义上，局部Moran's I指数讨论路段及路段的邻域某属性项的相关性，同全局Moran's I指数相比，局部Moran's I指数能够通过统计显著性检验对聚集情况进行定位。对于网络空间内的任意一个网络实体单元其局部 Moran's I统计量计算如下：

式中，xi是研究区域内观测的属性值，n是研究区域内的基本研究元素的个数，x是xi的均值，Wij是元素i和j的权重矩阵。权重W有两种计算方式：二元邻接矩阵和距离邻接矩阵。在二元邻接矩阵中，如果元素i和j邻接，则Wij为1，如果元素i和j不邻接，则Wij为0；在距离邻接矩阵中，Wij的值与元素i和j的距离成反比，距离越大Wij越小，距离越小Wij越大。其中，I的值可以通过一种类似Pearson相关系数的方法进行计算，其取值范围为[-1,+1]，值为-1左右表示强的负相关，值为+1左右表示强的正相关，值为0左右表示不存在空间相关性。某空间位置i和其邻域内的其他单元的空间关系有4种类型：低-低、高-高、低-高、高-低，低低和高高为正相关，低高和高低为负相关。满足统计显著性情况下，若某路段及其邻域内核密度估计值均较高，即高-高类型空间关系。通过合并高-高定长单元，形成交通事故易发路段。

3 实验分析

本文进行路网约束下的核密度估计和平面核密度估计，并对网络核密度估计的结果进行网络Moran's I统计判读，对交通事故点分布的聚集情况进行评价。

3.1 核密度估计

根据《城市道路交通规划设计规范》，城市主干道为45～55 m，次干道40～50m，支路15～30m。本文道路抽象成线性要素，交通事故点定位在道路网上，那么r和lixel的最小值均应大于行车车道宽度。为了对比平面核密度估计和网络核密度估计在探测网络空间点事件分布模式的不同，并讨论不同lixel长度、搜索半径对核密度估计的影响，本文实验设计了四项实验，其实验参数见表1。实验I和实验II都采用10m定长分割路网，分别设定40m和200m搜索半径，均采用Gaussian函数讨论搜索半径确定的分析尺度对聚类结果的影响。实验II和实验III均采用200m搜索半径，分别设定10 m和40m的定长，讨论定长确定的核密度估计分辨率对聚类结果的影响。实验IV采用平面核密度估计方法，分别用40 m的定长和200 m的搜索半径，与实验III的网络核密度估计结果进行对比。

表1 实验方法及参数Tab. 1 Methods and parameters in experiments

实验I、实验II、实验III和IV实验的核密度估计结果见表2，其中，COUNT为lixel切割后的定长个数。当lixel为10 m，搜索半径越大，核密度估计尺度越大，核密度估计值越大，估计值的标准偏差越大，越能体现事故的聚集程度。

表2 实验结果统计表Tab. 2 Results of experiments

分级统计图法是反映现象集中程度的地图表现方法之一，根据核密度估计实验结果，生成核密度估计分级图，直观表现交通事故的分布情况。下面分别从整体和局部两个方面对比分析不同的参数、不同的方法对机动车碰撞空间分析的影响。

在整体空间上，图2a中机动车碰撞的核密度值分布整体呈零散分布，密度值较高的路段主要分布在中心城区的几条主干道上，其分布形态同事故的定位点形态吻合。图2b中机动车碰撞的核密度估计值的整体呈明显的高低聚集，其中主城区如江岸区、江汉区的核密度估计值较高，汉阳大道、中山大道、中北路、解放大道等路段的核密度估计值。图2d中核密度估计值呈现局部面状聚集分布，其分布情况同图2a有相似之处，但是其聚类范围较大，其精细程度不及图2a中的网络核密度估计值的结果。对比发现图2d和图2c，所有的核密度估计方法都可以表现机动车碰撞事件的空间分布情况，虽然都可以揭示部分机动车碰撞的热点区域，但是平面核密度估计和网络核密度估计的表达结果差别很大，平面核密度表面覆盖整个区域，而网络核密度表面仅覆盖道路网络部分。在图2d中，平面核密度估计也可以表达机动车碰撞聚集的基本情况，其基本形态与图2c有着类似的形态，但是在局部细节的表现上不足图2c；同时，与网络核密度相比，平面核密度可能存在过度估计。

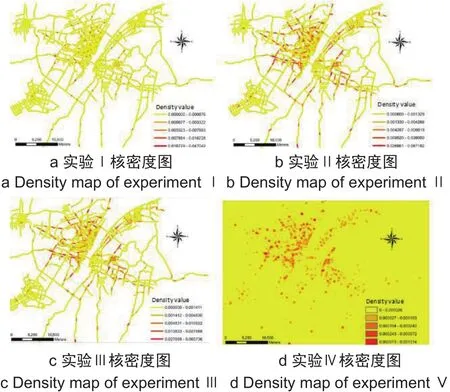
图2 核密度估计可视化情况Fig. 2 Maps of kernel density estimation results

为了进一步展现不同lixel长度、不同搜索半径对平面核密度估计、网络核密度估计结果的影响，在原始的比例尺下，选择同一局部区域（即钟家村附近，汉阳大道与鹦鹉大道交会周边），对不同参数、不同方法的机动车碰撞格局分布进行展示，如图3所示，其中，图3a～图3d分别是图2的局部方法，其分级情况、方位与图2相同。对比图3a、图3b，也就是lixel同为10 m，搜索半径分别为40 m和200 m，两种方法的局部表现力差别较大。对于较小的搜索半径，其表达的局部变异细节较多，变化信息展现的越丰富；对于较大的搜索半径，其表达的局部细节存在一个综合的过程，即将邻域中的聚类细节合并更大的聚类，聚类的细节信息展现减少，从而密度变化光滑，地图展示的直观效果稍好，而且减少过多细节可以表现相对大尺度的网络空间分布状态。对比图3b、图3c，也就是lixel分别为10 m和40 m，搜索半径分别为200 m，对于较小的lixel，局部细节表现更多，但是计算量也相对较大；对于较大的lixel，局部表现相对不足，计算量较小。

图3 核密度估计结果局部分布情况Fig. 3 Local distribution of kernel density estimation results

3.2 网络核密度估计结果的局部Moran's I统计检验

通过核密度估计结果的局部空间统计分析，可以对核密度估计方法进行定量解释，将邻域内具有核密度估计值较高并且正向空间相关的道路基本定长进行合并，标记为交通事故易发路段。本组实验包含2项实验，见表3，实验V和实验VI的数据输入值是实验II和实验III的每个道路基本定长单元的核密度估计值，通过Conditional Permutation的模拟方法，模拟99次，计算每个基本定长的Moran's I统计量。根据局部Moran's I统计结果，讨论不同显著性水平下高-高道路基本定长的个数和高-高道路的个数，其结果见表4。实验V和实验VI都表明随着显著性水平的降低，高-高基本定长个个数不断增加，但是增长幅度却逐渐趋于平缓，0.05显著性的定长增幅最大。不论在哪一个显著性区间，实验V的高-高基本定长数都是实验VI的高-高基本定长数的相对固定倍数范围内（2.6～2.8倍），表明道路基本定长固定的影响交通事故核密度估计值。

实验表明当lixel设定为40 m时，能够相对精确地识别交通事故发生相对较高的路段，本文选择实验VI的结果，对武汉市道路交通事故发生相对较高的路段进行判别，在0.01显著性水平下按照交通事故易发程度的高低进行排序，形成武汉市交通事故易发路段列表，其中前30个事故易发路段见表5。

表3 局部Moran's I实验及参数Tab. 3 Parameters in local Moran's experiments

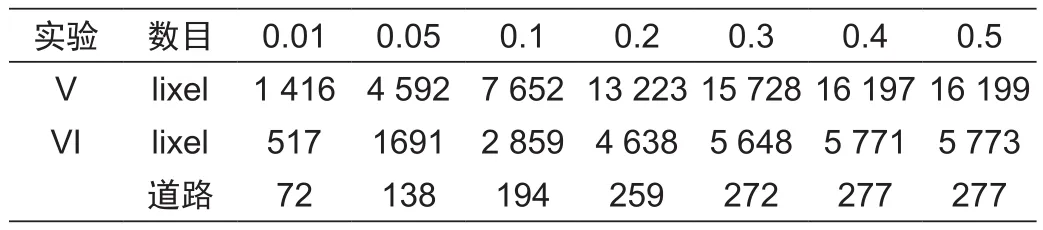
表4 不同显著性水平下高-高道路基本定长的个数Tab. 4 Numbers of high-high road segments(roads) under diあerent significance level

表5 实验VI中0.01显著性水平下H-H前30个路段列表Tab. 5 Top 30 roads of H-H under significance level of 0.01 in experiment VI

结果表明，汉沙公路是武汉市最危险的路段，其机动车碰撞次数的密度值和Moran's I统计值都是最高的，且根据交通管理部门的机动车碰撞分析报告和机动车碰撞新闻事件的报道认为，汉沙公路也是机动车频发路段，说明了本研究的方法在机动车碰撞热点路段探测过程中的有效性。由于该热点路段位于汉蔡高速入口，机动车行驶速度较快车辆较多，从而容易发生机动车碰撞事件，近些年来该路段一直在进行安全隐患的排除和管理的加强。此外，由于江岸区路网的密集性和复杂性，危险路段也相对集中于江岸区。

4 结束语

交通事故作为人类财产和生命安全的一个重要威胁，其中交通事故的热点路段排查是城市交通管理中的重要一个环节。核密度估计方法作为检测交通事故易发路段的有效方法，在分析沿网络约束点事件时存在偏差，本研究以武汉市为例将平面核密度估计方法扩成为网络核密度估计方法，并使用网络局部Moran's I对核密度估计结果进行测度。研究表明，武汉市交通事故呈现了明显的沿路网聚集的趋势，基于网络核密度估计和网络Moran's I的方法可以有效地从道路尺度精确定位交通事故的聚集情况，并探测机动车碰撞热点路段，弥补了传统核密度估计方法作为可视化工具而缺少统计显著性评价的缺点，更具现实指导意义。然而本文仅采用网络局部Moran's I统计量对路网约束核密度估计结果进行定量统计，并未对交通事故的影响因素与交通事故的分布格局之间的相互作用进行深入讨论，在后续的研究中还需要充分考虑交通流量、路网通达性、土地利用情况等因素，将其作为综合权重，修正网络核密度估计方法，以期更加精准地对交通事故热点路段进行评估。