基于剖分表达结构的雷达探测范围计算方法

袁 越，程承旗，童晓冲

(1. 北京大学 工学院，北京 100871；2. 信息工程大学 地理空间信息学院，河南 郑州 450001)

0 引 言

作为战场基本装备的雷达不仅在军事上发挥着至关重要的作用[1-3]，而且被广泛应用于社会经济发展和科学研究领域[4-7]。雷达利用电磁波探测目标，而电磁波在空间的传播距离受到诸如地形、大气、电磁干扰等多种环境因素的影响。如何准确计算出真实环境下雷达探测范围具有重要意义。

目前，针对雷达探测范围算法的研究主要分为基于几何光学的算法以及基于数学建模的算法两大类：

1）基于几何光学的算法主要考虑了地形对雷达探测范围的影响。孟国明提出把受地形影响的雷达采样点在直角坐标系中沿纵坐标方向向上修正的方法[8]，该方法简单高效，但修正精度过低；陈鹏等在此基础上，提出对连续山峰的处理算法[9]，该算法虽然提高了计算精度，但对不同地形的适应性不强；白玉兵等基于几何光学原理，提出单峰和多峰地形影响下雷达探测范围的修正算法，实现了对复杂地形影响的修正[10]，该算法对复杂地形适应性较强，但算法复杂度高；邱航等提出了一种基于混合采样的地形影响下雷达作用范围三维建模方法，在方位角方向以地形最小分辨率网格为基准进行采样，在俯仰角方向以雷达波束特征点为基准分区域采样[11-12]，该方法在保证模型准确性的同时降低了计算开销。

2）基于数学建模的算法可以综合考虑多种环境因素对雷达探测范围的影响。Awadallah等运用边界积分方程解决三维传播问题[13-14]，该方法在范围比较大的情况下难以达到实用；张敬卓等综合考虑了地形、大气等自然因素以及干扰机等人为因素的影响，基于高级传输模型APM，给出了复杂环境下雷达三维探测范围的数学模型[15]；杨超等提出基于抛物线方程的雷达探测范围三维建模，给出了考虑因素较为全面的雷达电磁波传输衰减数学模型[16-17]。

综合分析这些研究可以发现，虽然基于数学建模的方法考虑因素较为全面，但该方法普遍存在计算量大、普适性不强等不足。因此，目前有关雷达探测范围算法的研究主要集中在基于几何光学的、考虑地形影响的雷达探测范围计算上面。

然而，现有算法考虑地形影响后，需要不断计算从雷达中心点出发的射线与DEM表面的相交运算，即变成了三维空间中的线面相交问题，计算量大且算法复杂度高。针对上述问题，本文提出一种基于剖分表达结构的雷达探测范围算法。该算法在计算地形影响下的雷达探测范围时，将雷达探测范围和地形数据的覆盖范围均剖分化，将空间线-面相交运算、面-面相交运算转化为剖分体元编码集合的求交运算，将复杂的运算变得简单，大大提高了计算效率。

1 剖分表达结构

剖分表达结构：用一组（一个或多个）规则化后的剖分单元集合对空间实体进行表达，表达的结果用剖分编码集合的形式来表示，其本质是一种聚合表达模型。

为便于表述，本文约定：“L”代表“剖分体元层级（Layer）”，“C”代表“剖分体元集合（Collection）”，“V”代表“剖分体元（Vexel）”，“lon”代表“经度（longitude）”，“lat”代表“纬度（latitude）”，“h”代表“大地高（height）”，“T”代表“地形（Terrain）”，“r”代表“雷达（radar）”，“D”代表“DEM”，“O”代表“叠置（Overlay）”。

剖分表达结构的整体架构包含概念层、逻辑层和物理层，它们之间互相映射，构成一个有机完整的体系。

其中，概念层是对现实世界中点、线、面、体实体以及空间场对象的格网化抽象描述。选定合适的剖分框架后，在立体剖分表达结构下，剖分单元表现为空间中的一个立方体区域，称为剖分体元，空间中的任意对象均可由一个或一组剖分体元聚合而成。如图1所示。

图1 剖分表达结构概念层Fig. 1 Concept layer of subdivision expression structure

逻辑层建立在概念层的基础之上，对不同种类的空间对象分别进行逻辑抽象，定义不同种类空间对象逻辑模型的数学表达。在真实空间中并不存在抽象的点、线，任何空间对象都有一定的尺度，可用层级n下m(m≥1且m为整数)个剖分体元的集合表示：

物理层面向操作的实体存储结构与约束设计，重点解决剖分实体在计算机中的底层描述。通过建立以实体ID为主键的“对象表”，以及以格网编码为主键的“格网索引表[18]”，为格网化的实体提供物理存储与查询等操作规则，建立地理空间在计算机存储空间中的映射关系。表1是剖分表达结构的物理层，其中的格网编码形式参考文献[19]。

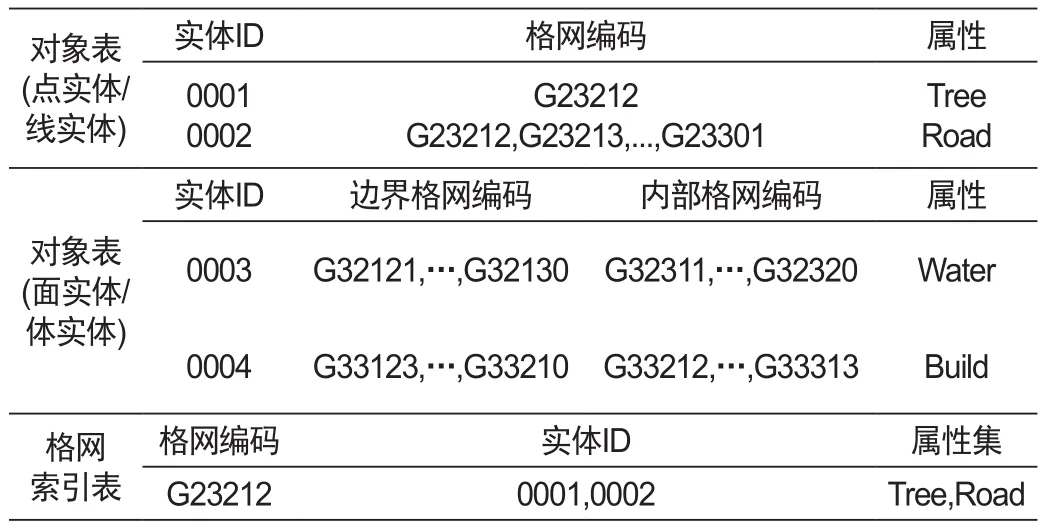
表1 剖分表达结构物理层Tab. 1 Physical layer of subdivision expression structure

2 基于剖分表达结构的雷达探测范围算法设计

自由空间中，当不考虑任何环境影响时，雷达在确定的俯仰角θ，方位角φ上的探测距离由雷达方程[20]确定：

式（2）中，Pt为发射功率；Pr为接收功率；Ft是发射天线到目标的方向图传播因子；Fr是接收天线与目标的方向图传播因子；Gt为发射天线功率增益；Gr为接收天线功率增益；σ是雷达目标的截面积；λ是雷达波长。根据雷达基础参数及雷达方程，计算出雷达在俯仰角θi(1≤i≤m,m为俯仰角采样数)、方位角φj(1≤j≤n,n为方位角采样数)上的探测距离，由此得到雷达探测范围。

在此基础上，为进一步得到地形影响下的雷达探测范围，传统方法需要不断进行雷达探测范围与DEM表面的相交运算，计算效率低。基于剖分表达结构的雷达探测范围算法则利用编码集合的交、并、补等查询操作代替浮点计算，从而提高计算效率。

2.1 多尺度统一建模

为计算基于剖分表达结构的地形影响下雷达探测范围，首先需要将自由空间中雷达探测范围以及DEM格网数据转换为剖分表达结构下某一层级的体元集合，其中剖分层级可以根据实际情况进行选择。这个过程即为“多尺度统一建模”，具体分为两步：雷达探测范围建模和DEM格网数据建模。

2.1.1 雷达探测范围建模

雷达探测范围建模具体步骤如下：

步骤1：选择剖分框架。根据实际应用的需求，选取适当的剖分框架，以此为基础构建剖分表达结构。剖分框架的选取是多尺度统一建模的基础。

步骤2：确定剖分层级。具体分为以下两种情况：

①要求剖分体元平均边长小于δ。此时要在满足要求的前提下，选择尽可能大的网格所对应的层级作为剖分层级L，即满足SideL≤δ＜SideL-1（其中，SideL表示层级L下的剖分体元平均边长）。这样既满足要求，又避免了网格冗余。

②未对剖分体元边长设定要求。此时根据DEM数据采样间隔δ＇来确定剖分层级L，基本方法同①。

步骤3：雷达探测范围垂直方向剖分。图2a所示的是雷达空间探测范围，其中点O为雷达中心，点A为雷达探测范围最高点，R为雷达探测范围半径，层级L下的剖分体元边长为SideL。那么在垂直方向上，用N(N=Int(R/SideL))个圆心在OA轴上、且平行于地表的圆面对探测范围进行分割，其中的第i个圆面用Si(1≤i≤N)表示。根据勾股定理，Si的半径

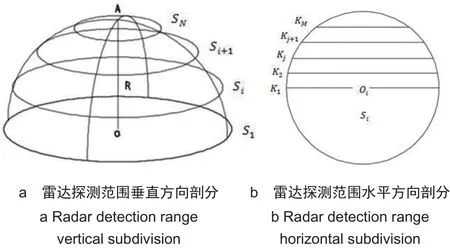
图2 雷达探测范围剖分示意图Fig. 2 Diagram of radar detection range subdivision

步骤4：雷达探测范围水平方向剖分。这一步是将步骤3中划分得到的N个圆面进行格网化填充。图2b所示的是圆面Si，其圆心为Oi，半径为Ri。用M(M=Int(Ri/SideL))条平行于直径的直线对北半圆进行划分，其中第j条直线用Kj(1≤j≤M)表示，其长度。参考“扫描线填充算法[21]”的思想对圆面Si进行格网化填充。类似地，对所有圆面进行格网化填充后，得到雷达探测范围剖分体元集合Cr，完成雷达探测范围建模。

2.1.2 DEM格网数据建模

DEM格网数据建模步骤如下：

步骤1：DEM区域范围计算。根据DEM数据提供的左下角点坐标、采样间隔、行列数等参数，依次计算出每个格网上表面4个顶点的经纬高坐标，得到每个格网的区域范围。

步骤2：DEM内部格网填充。在步骤1的基础上，采用雷达探测范围建模的思想，从垂直方向和水平方向上对DEM进行内部格网填充，完成DEM格网数据建模。

通过雷达探测范围建模和DEM格网数据建模两大步骤，完成多尺度统一建模。在此基础上，进一步设计地形影响下雷达探测范围算法以及多雷达探测范围叠置算法。

2.2 地形影响下雷达探测范围算法

雷达发射的电磁波在空间传播受到地形的遮挡会被反射，从而出现雷达波束被部分或完全截断的情况。一般可分为以下几类，如图3所示。

图3 雷达探测范围受地形影响的三种情况Fig. 3 Three cases of radar detection range under the influence of terrain

图3 中，点O表示雷达中心；用虚线围成的椭圆A表示不考虑地形影响时，雷达覆盖范围的部分截面；曲线B和X轴围成的曲面表示地形起伏的截面。图3的具体含义如下：

图3a：雷达周围地势比较平坦，基本没有起伏，地形不会对雷达波束造成遮挡。此时雷达探测范围受地形的影响可以忽略不计。

图3b：雷达周围地形起伏比较大，且雷达位于最高地势。此时雷达波束不会被地形遮挡，雷达探测范围受地形的影响也可以忽略不计。

图3c：雷达周围地形起伏比较大，且雷达位于低地势。此时雷达发射电磁波会被地形完全截断，最终得到的雷达探测范围如图3中SOMN所示。

对于图3a和图3b而言，由于雷达波束没有被截断，地形对雷达探测范围的影响可以忽略不计。此时，计算出雷达探测范围后，只需将其转换为指定层级的剖分体元集合即可。此时基于剖分表达结构的雷达探测范围算法用【算法1】表示，详细步骤如下：

【算法1】

步骤1：输入雷达的基本参数，包括发射功率Pt、接收功率Pr、发射天线功率增益Gt、接收天线增益Gr、雷达波长λ、雷达目标的截面积σ。据此计算出Rmax。

步骤2：根据空间中点(θ,φ)的实际场强与自由空间中该点所存在场强的比值，确定方向图传播因子F(θ,φ)。

步骤3：由步骤1计算出的Rmax和步骤2计算出的F(θ,φ)，根据公式（2）计算出俯仰角θ(θ∈[0°,90°])、方位角φ(φ∈[0°,360°])方向上的最大探测距离R(θ,φ)，得到雷达探测范围。

步骤4：将步骤3中得到的雷达探测范围进行多尺度统一建模，转化为层级L下的剖分体元集合Cr。Cr即为基于剖分表达结构的雷达探测范围。

对于图3c的情况，由于雷达处于低地势，雷达波束被完全截断，雷达探测范围SOMN=SOMPN-SMPN。此时基于剖分表达结构的雷达探测范围算法用【算法2】表示，它只需在【算法1】的基础上添加步骤5和步骤6步骤。

【算法2】

步骤1～步骤4同【算法1】。

步骤5：对DEM格网数据进行多尺度统一建模，转换为层级L下的剖分体元集合CD。

步骤6：设剖分体元集合CT=Cr-Cr∩CD。则CT表示基于剖分表达结构的地形影响下雷达探测范围。

2.3 多雷达探测范围叠置算法

由于不同雷达的参数不同，它们探测范围的包络曲面方程也不一样。用传统方法对这些曲面求交集会相当复杂。基于剖分表达结构计算则会使算法复杂度大大降低。具体算法步骤如下：

【算法3】

步骤3：雷达M和雷达N探测范围叠置区域即为剖分体元集合CO，其中，

3 实验与分析

考虑到目前雷达最大探测距离已达数千千米（如“萨德[22]”），本文拟选取全球剖分网格结构作为基础。目前，国内比较有代表性的是“2n一维整型数组的全球经纬度剖分网格”（Geographical coordinates Subdividing grid with One dimension integral coding on 2n-Tree，简称GeoSOT[23]），本文选择对其进行立体扩展后的GeoSOT-3D[24]剖分框架进行实验。

GeoSOT-3D剖分框架是一套涵盖地上6万多千米、地下直到地心的空、天、地、地下、水下一体的空间信息表达框架结构，可有效地表达数千千米范围的雷达覆盖区域，具有全球统一剖分、二三维一致性、易于空间实体数据建模等优势。基于该框架形成的GeoSOT-3D剖分编码具有编码唯一性、多尺度性、二进制一维整型等特性。

根据GeoSOT-3D网格的剖分规则以及编码方法，当要求剖分体元边长小于δ时，可由公式（3）确定剖分层级L，相应的剖分体元边长SideL由公式（4）确定：

以此为基础，根据【算法1】～【算法3】，完成下面实验。

3.1 实验环境

硬件环境：Intel(R)Core(TM)2Quad CPU、4GB内存、NVIDIA GeForce 9500GT显卡、2GB显存；

软件环境：Windows7专业版32位操作系统、谷歌地球（7.1.8.3036版）二次开发；

编译环境：Microsoft Visual Studio 2010、C++语言；

数据环境：雷达基础参数见表2；本文采用了模拟DEM的效果，测试不同类型地形（图3中不同情况）对雷达探测范围计算的影响。

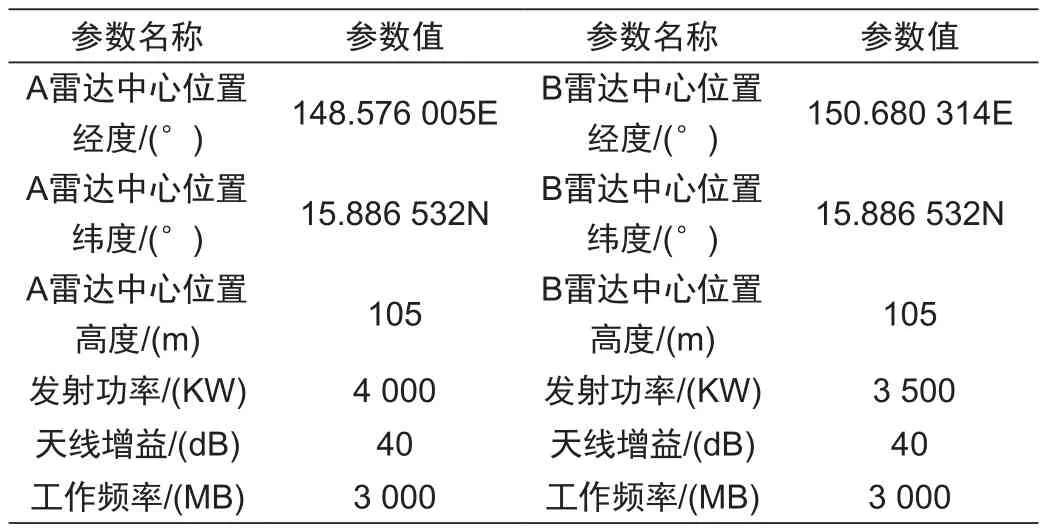
表2 实验雷达基础参数表Tab. 2 Basic parameters of experimental radar

3.2 实验结果

3.2.1 地形影响下雷达探测范围计算试验

根据【算法1】和【算法2】进行地形影响下雷达探测范围计算实验。为验证本算法的正确性和高效性，实验选取传统基于几何光学的雷达探测范围算法作为对比实验。

设层级L下的剖分体元经距为DLonL、纬距为DLatL、高距为DHL、考虑地形后雷达探测范围体元个数为Num，则本算法计算得到的地形影响下雷达探测范围体积V1可用公式（5）表示[25]；设雷达探测范围半径为R，DEM采样间距为SideD，传统方法计算得到在雷达探测范围内的第i(i=1,2,…,n)个DEM格网的高程为Hi，则传统算法计算得到的地形影响下雷达探测范围体积V2可用公式（6）表示[26]。本算法计算的相对误差ε可由公式（7）进行计算。具体实验结果见表3。

表3 地形影响下雷达探测范围计算结果表（DEM格网个数为300×300）Tab. 3 Calculation results of radar detection range under the influence of terrain(300×300 DEM grids)

从表3中可以看出，当剖分层级比较低（15级）时，剖分体元平均边长（2 km）较大，相对误差较高（33.457%）；逐步增加剖分层级后，剖分体元平均边长随之变小，此时相对误差陡降至5%以下，剖分层级为19级时相对误差甚至降至1.1%。由此可见，本算法计算的相对误差随着剖分层级的增长逐步降低，剖分层级为15级以上时基本可以满足计算精度的要求，见表4。

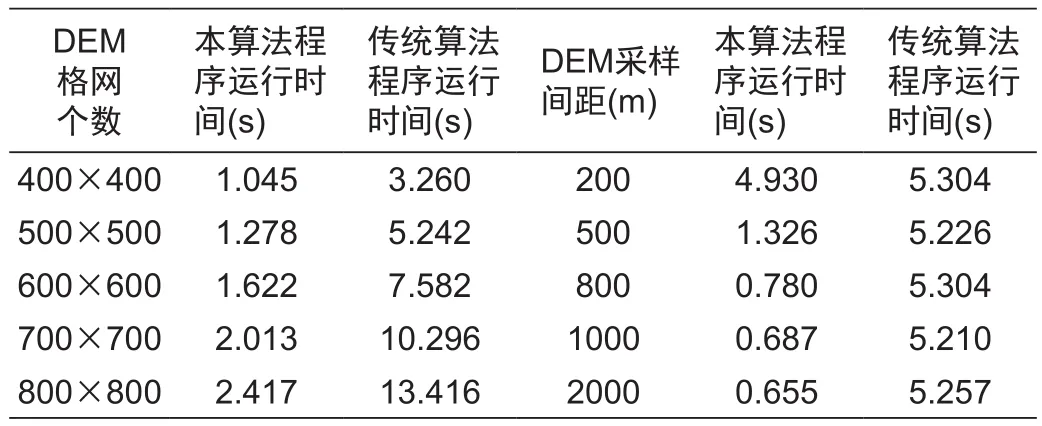
表4 本算法与传统算法计算效率对比表Tab. 4 Calculation eきciency comparison between this algorithm and traditional algorithm

对表4进行分析可以得出以下结论：

1）当保持DEM采样间距不变（均为500m），本算法和传统算法程序运行时间都随DEM格网个数的增加而增加，但传统算法增加幅度更大，如图4a所示。

2）当保持DEM格网个数不变（均为500×500），本算法程序运行时间随DEM采样间距增加而急速降低，传统算法程序运行时间基本不随DEM采样间距变化，且传统算法平均耗时约为本算法平均耗时的5倍，如图4b所示。

综合以上可知，本算法较传统算法而言是高效的。

图4 程序运行时间对比图Fig. 4 Comparison gragh of program running time

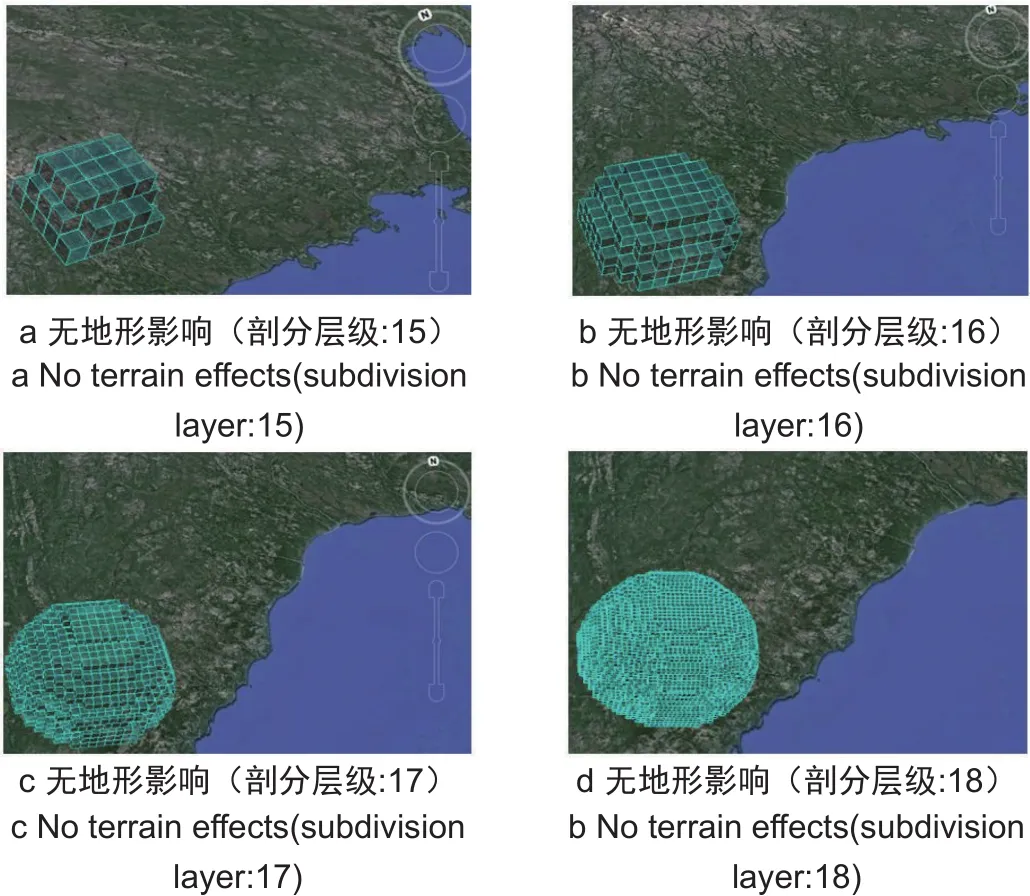
图5 无地形影响时雷达探测范围可视化效果Fig. 5 Visualization of radar detection range without terrain eあects

图6 地形影响下雷达探测范围可视化效果图Fig. 6 Visualization of radar detection range under the influence of terrain

最后的可视化效果如图5、图6所示，其中蓝色网格集合表示雷达探测范围，黄色网格集合表示地形。

3.2.2 多雷达探测范围叠置计算试验

根据【算法3】进行两雷达探测范围叠置计算实验，实验结果见表5。其中，V3表示本算法计算得到的两雷达探测范围体积[25]，V4表示传统方法计算得到的雷达探测范围体积[27]，相对误差ε＇=(|V3-V4|)/V4。

表5 多雷达探测范围叠置计算结果表Tab. 5 Calculation results of multi-radar detection range

从中可以得出以下结论：

1）随着剖分层级的增加，剖分体元粒度逐渐变小，雷达探测范围的剖分体元个数逐级递增，并且相邻两级增长倍数约为8倍，符合选用的GeoSOT-3D剖分框架的八叉树递归剖分特性；

2）如图7b所示，程序相交计算时间与相交体元个数近似呈正比关系，说明该算法是稳定的；

3）算法计算的相对误差随剖分层级的增加逐渐减低，当剖分层级为15级以上时，相对误差稳定在3%以下，满足大多数应用场景下的精度要求。

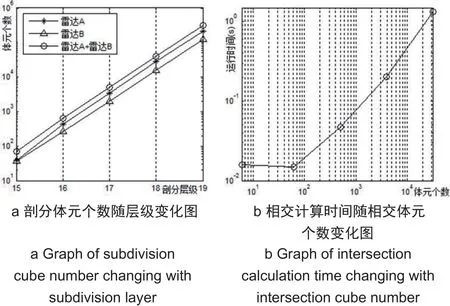
图7 雷达探测范围计算结果图Fig. 7 Calculation results graph of radar detection range

最后的可视化效果如图8所示。其中白色网格集合表示雷达A探测范围，黄色网格集合表示雷达B探测范围，红色网格集合表示两雷达探测范围的交集。

图8 两雷达探测范围可视化效果图Fig. 8 Visualization of two radar detection ranges

4 结束语

本文提出了一种基于剖分表达结构的雷达探测范围算法。该算法以剖分表达结构为基础，通过多尺度统一建模、编码集合的查询操作等步骤，实现了地形影响下雷达探测范围的计算以及多雷达叠置分析计算，并通过实验验证了算法的正确性、可行性和高效性。本文算法适用于无地形影响或雷达波束被地形完全截断情况下的雷达探测范围计算，但是值得说明的是，该算法并没有考虑如图9所示雷达波束被地形部分截断的特殊情况，虽然这种情况在雷达源布设的时候一般会尽量避免，但从几何学的角度仍可能出现。在下一步的研究中，会进一步完善算法，给出数学理论推导的误差公式和实际检测的误差，发展适应地形连续变化的非规则网格剖分方法，适应更多的特殊情况。

图9 雷达波束被部分截断Fig. 9 Radar beam is partially truncated