有缺失数据的加权指数总体参数估计的渐近性

李开灿，张文强

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

有缺失数据的加权指数总体参数估计的渐近性

李开灿，张文强

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

依照随机变量变换可以重新参数化的思想，得到了一种加权指数分布总体在具有缺失数据情况下参数的极大似然估计，利用中心极限定理和相关的极限理论，证明了这种估计量的强相合性和渐近正态性。

加权指数分布；缺失数据；极大似然估计；渐近正态性

0 引言

指数分布是可靠性分析中重要的分布，因为许多电子元器件的寿命可以用它来刻划。近年来由于对系统可靠性研究的深入，人们觉得以前的单参数或双参数指数分布还有进一步发展的需求，例如在并联系统的可靠性研究中，若并联系统元件有不同的寿命分布，那么系统的可靠性分布就不是单参数或双参数指数分布，文献[1]、[2]提出了两类加权指数分布，其实文献[1]、[2]的分布形式还可以进一步拓展，由于它不是本文研究的主题，我们暂且回避不谈。但是加权指数分布所具有的性质，特别是和指数分布类似的性质是需要研究的。

在双参数或单参数指数分布研究中，近期有许多文献研究了带有缺失数据类型的参数估计的统计性质。文献[3]研究了单参数且有缺失数据情行下参数估计的渐近性，文献[4]对具有部分缺失数据双参数指数总体的参数估计性质进行了讨论，文献[5]对单参数两指数总体带有缺失数据的参数估计问题进行了讨论，给出总体参数估计的渐近性质、参数相等的检验以及参数差的渐近置信区间。

本文的主要目的是研究文献[2]提出的加权指数分布在缺失数据下参数估计的渐近性问题。我们通过借助随机变量转化，得到一个新的包含原有参数的加权指数分布密度函数的机理，对密度函数中的未知参数重新参数化，进而得到了这个加权指数分布参数的极大似然估计，利用前面文献类似的方法及其大数定律和中心极限定理，本文证明了加权指数总体下参数极大似然估计具有的强相合性和渐近正态性。

1 加权指数分布概述

在概率论中，人们通过直接定义密度函数来描述许多常用的分布，文献[2]也这样给出加权指数分布。若随机变量Z有密度函数

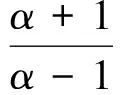
(1)

其中I(z>0)是示性函数，α>1，λ>0是常数，则称Z服从参数为α，λ的加权指数分布，记作Z～WE(α，λ)。

加权指数分布的产生机理文献[2]从并联系统做了一个全面的解释，现在从随机变量变换的方式给出产生原理。用X～Be(a,b)表示随机变量X服从Beta分布，其密度函数为

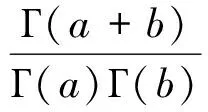
若随机变量U～Be(a,b),∀c>0,令U=e-2cV，用确定随机变量函数分布的常规方江(文献[6]不难导出新随机变量V的密度函数为

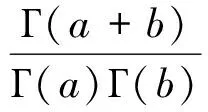
(2)

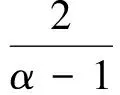
即得到加权指数分布的密度函数。这说明加权可靠指数分布可利用变量转化由Beta分布生成。

注记1 通常α称为形状参数，λ称为尺度参数.单独从分布密度(1)式可以认为α、λ是独立的，但是从产生机理不难发现，可以让它们有某种关联，这就是我们后面把这两个参数关联化的基础。

2 问题的假设与参数极大似然估计

在文献[1]、[2]都讨论了加权指数分布参数的极大似然估计，[2]还给出了极大似然估计的极限性质，本节给出(1)式下有缺失数据的参数估计。需要指出的是本文讨论的数据缺失机制都是完全随机缺失的，即MCAR，细节见文献[7].

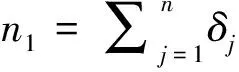
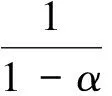
f(x,λ)=2λ(2λ+1)e-2λx(1-e-x)x>0

本文主要研究这类分布的极大似然估计及其渐近性质。

为了获得缺失数据下λ的极大似然估计，首先确定其观测到的数据X1,X2,…,Xn1的似然函数

从而对数似然函数为

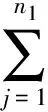
对数似然方程

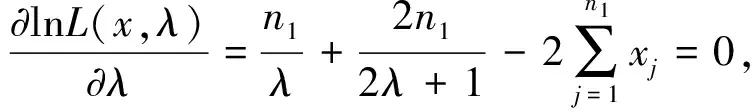
进一步可得方程的解

化简即可得λ的极大似然估计为

3 未知参数极大似然估计的渐近性质

在本节主要讨论上述有缺失数据的加权指数分布极大似然估计的渐近性质，为此先引入几个引理。

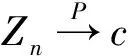
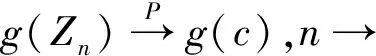
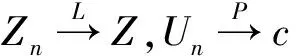
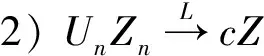
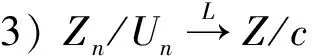
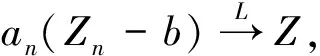
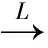
这几个引理的证明都可以在文献[8]中找到。

定理 在加权指数分布中，若参数和观察样本满足本文§2的条件，那么当n→∞时，(3)确定的极大似然估计有如下渐近性质，

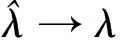
证明 由强大数定律可知当n→∞时，

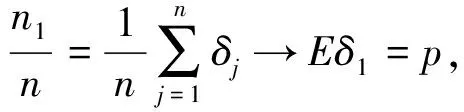
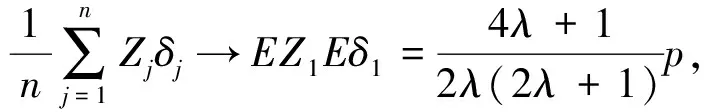
令函数

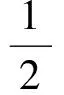
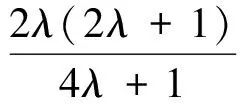
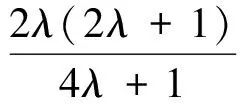
又由于

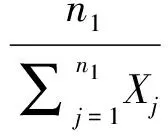
于是由引理1可得

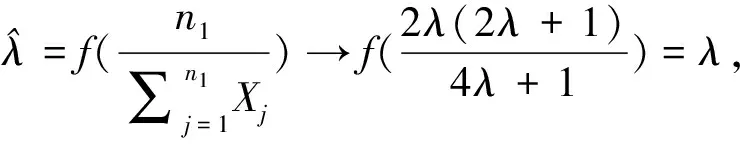
另一方面取函数

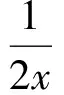
则

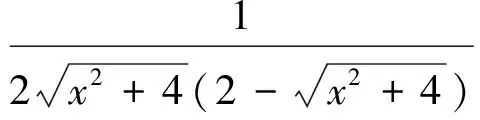
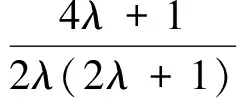
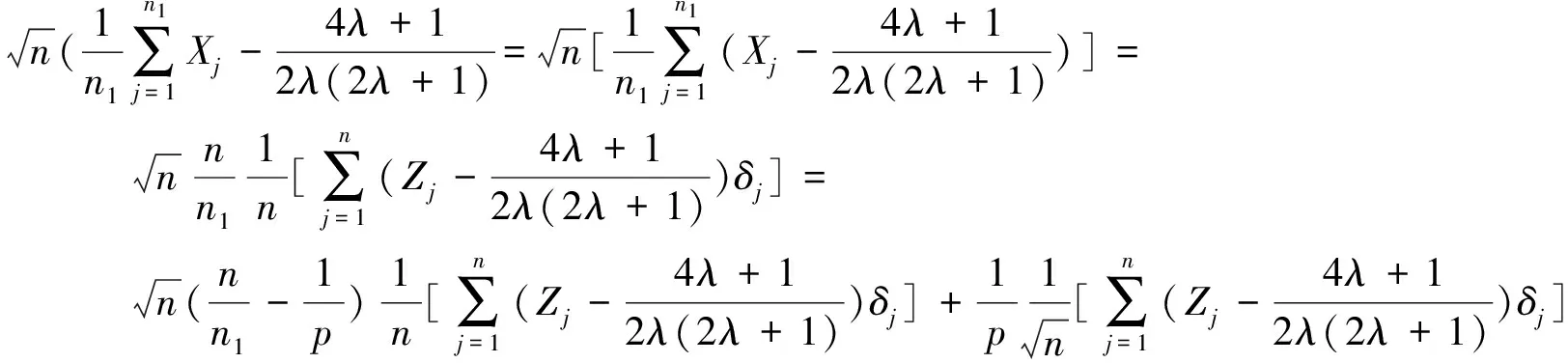
对于(4)式中的I2，由于

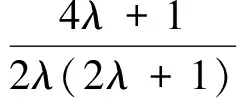
根据中心极限定理(见文献[6])

于是有

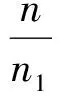
有

又由于

由引理3可知

证毕。

本文仅对加权指数分布在缺失数据情况下，利用所观测到的数据对总体参数进行极大似然估计，不过也只是运用特殊参数化才做出的极大似然估计并证明了它的强相合性和渐近正态性，类似文献[5]，我们也可以对参数化的两个加权指数总体带有缺失数据的参数是否相等进行检验以及作出参数差的渐近置信区间在此不一一讨论。另外，对加权指数分布若不进行特殊参数化，两个参数有缺失数据如何研究估计的渐近性质还有待进一步的研究。

[1]Rameshwar D Gupta, Debasis Kundu. A new class of weighted exponential distributions[J]. Statistics-A Journal of Theoretical and Applied Statistics, 2009,43(6):621～634.

[2]刘大飞，李开灿.一类加权可靠指数分布[J].数学杂志，2013,33(4)：689～696.

[3]刘银萍.具有部分缺失数据两个指数总体的估计和检验[J].吉林大学学报(理学版).2002.40(3):255～257.

[4]马明月，宋立新.具有部分缺失数据两个双参数指数总体的估计[J].吉林师范大学学报(自然科学版)，2004,(2):14～18.

[5]苏 曦，郭鹏江，夏志明.两指数总体带缺失数据的参数估计与检验[J].三峡大学学报(自然科学版),2011,33(4):101～103.

[6]李开灿，蔡择林.概率论[M].武汉：湖北科学技术出版社，2009.

[7]Little R J A, Rubin D B. Statistical Analysis with Missing Date[M].2nd edition. New York: Wily,2002.

[8]茆诗松，王静龙，濮晓龙.高等数理统计(第二版)[M].北京：高等教育出版社,2006.

Abstract: By the ideal to transform expression of the random variable that one can do reparametrization for the old parameter in distribution, This paper gets the maximum likelihood estimation for the weighted exponential distributions with missing data. Further, using the limiting theory relating to the central limit theorem, the strong consistency and asymptotic normality of the estimation are also proved.

Keywords: the weighted exponential distribution; missing data; MLE; asymptotic normality

Theasymptoticalpropertyontheestimationofweightedexponentialdistributionwithmissingdata

LI Kai-can, ZHANG Wen-qiang

(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002,China)

O212.2

A

2096-3149(2017)03- 0001-05

10.3969/j.issn.2096-3149.2017.03.001

2017—06—02

国家自然科学基金资助项目(11471105)

李开灿(1962— )，男，湖北武汉人，教授，研究方向为多元统计分析.