丝杠冷滚打成形参数控制研究

李玉玺 李 言 崔莅沐 杨明顺 肖继明 崔凤奎

1.西安理工大学机械与精密仪器工程学院，西安，710048 2.河南科技大学机电工程学院，洛阳，471003

丝杠冷滚打成形参数控制研究

李玉玺1李 言1崔莅沐1杨明顺1肖继明1崔凤奎2

1.西安理工大学机械与精密仪器工程学院，西安，710048 2.河南科技大学机电工程学院，洛阳，471003

建立了丝杠冷滚打成形的有限元模型，使用ABAQUS软件模拟其成形过程。首先在仿真结果的基础上，设计正交试验，研究冷滚打过程中工艺参数对滚打深度和隆起高度的影响关系；然后分别建立滚打深度和隆起高度与工艺参数之间的多元回归模型，并进行显著性检验；最后利用自行设计的滚打装置进行丝杠冷滚打试验，验证了模型的有效性。研究结果为通过控制工艺参数形成精确的零部件轮廓提供理论基础，对丝杠冷滚打成形有重要的指导意义。

丝杠；冷滚打；金属流动；正交试验

Abstract: A FEM model of the lead screw cold roll-beating forming processes was built, the ABAQUS software was used to simulate the forming processes. Firstly, based on simulation results, the orthogonal test was designed, influences of processing parameters on forces, beating depths and bulging heights of cold roll-beating processes were studied. Then multivariate regression models of beating depth and bulging height to process parameters were established, and significance tests for regression effects were carried out. Finally, with the self-developed experimental device, lead screw cold roll-beating experiments were carried out to verify the effectiveness of the models, which is of important guiding significances for forming accurate profiles of lead screw by control processing parameters.

Keywords: screw; cold roll-beating; metal flow; orthogonal test

0 引言

随着世界制造业竞争的日益加剧，绿色、节能、精密高效的塑性成形加工技术已成为当今制造业研究和发展的重点领域之一[1-2]。

高速冷滚打成形技术是利用金属固有的塑性，使用特定廓形、高速旋转的滚打轮对毛坯进行逐点断续滚压和击打，使坯料表层金属产生塑性流动，并利用滚打轮与坯料之间的相对运动关系产生累积效应，最终形成预定形状要求的一种无模无约束自由的塑性成形技术。研究表明，高速冷滚打成形方法具有设备吨位小、节能、成形过程柔性好等特点[3-4]。前期研究[5-6]主要对花键、齿轮、丝杠等功能表面的成形原理、有限元分析、动力学仿真以及设备原型等方面进行探索，初步验证了高速冷滚打成形工艺的可行性和优越性，对工件成形过程中金属的变形机理以及影响成形表面形状和尺寸的成形力的变化规律亟需深入探索和研究。

在丝杠高速冷滚打过程中，研究主要工艺参数对丝杠成形的影响规律，探索丝杠高速冷滚打成形的工艺参数选择准则，为冷滚打加工技术的实际应用提供理论指导，具有明确的工程实际意义[7-8]。

1 丝杠冷滚打成形原理

丝杠冷滚打加工是通过具有一定形状的滚打轮对丝杠毛坯进行局部断续滚压和击打，使毛坯产生塑性变形，通过累积效应，在工件上形成丝杠螺旋滚道[9-10]。其中，滚打轮安装在高速旋转的滚打轴上，并可绕自身轴线自转。滚打轮接触工件的瞬间，在工件与滚打轮之间摩擦力的作用下，滚打轮自转，实现滚打轮和工件之间的滚动，原理如图1所示，β为丝杠螺旋升角。当滚打轮击打工件即滚打轮与工件接触时，滚打轮自转速度由接触时的摩擦力和工件公转速度决定，滚打轮和工件之间为纯滚动运动，保证了丝杠成形件的表面质量和滚打轮的使用寿命。由冷滚打原理可知，丝杠冷滚打的主要运动有：滚打轴的旋转运动转速ns，工件的旋转运动转速nw，滚打轮的自转运动转速nr，滚打轮相对于工件的轴向进给运动s。滚打过程中，滚打轮可随滚打轴沿轴向以一定速度进给，工件以转速nw转动，且在固定位置做连续转动。

丝杠冷滚打成形是一个不断累积成形的过程，每一次滚打可以划分为以下四个阶段。

(1)第Ⅰ阶段：打入阶段。预先设定滚打的打入深度，滚打轮绕中心轴线做旋转运动并开始击打工件表面。由于滚打轮与工件轴向相互位置关系的影响，两者接触面积不大，打入深度较小。由图1可以看出，当工件回转中心点O1与滚打轮回转中心原点O3所在的直线与接触击打的滚打轮回转半径O2O3所在的直线重合时，是理论上的最大打入深度。根据上述理论位置的几何关系可以得到

D=r1-(|O1O2|-Rr-r)

(1)

式中，D为最大打入深度；r1为工件半径；|O1O2|为工件和滚打轮回转中心距；Rr为滚打轮回转半径；r为滚打轮半径。

(2)第Ⅱ阶段：稳定滚打阶段。滚打轮与工件接触面积增大，滚打轮不断滚压、击打和挤压工件表面，工件所受的径向、切向接触力不断增大，金属流动量增大并发生塑性变形；同时，已滚打出的金属表面出现加工硬化现象并沿着与滚打方向相反的方向移动，新滚打出的金属则沿着滚打方向推移和滚打轮两侧外翻，随着滚打的深入不断形成凹槽与凸起。

(3)第Ⅲ阶段：打出阶段。滚打轮不断远离工件表面，接触面积不断减小，滚打形成的凹槽与打入阶段的凹槽表面形状相近，在滚打轮对工件金属累积推移的作用下，金属向凹槽两侧流动，凸起量最大。

(4)第Ⅳ阶段：再次滚打阶段。第一次滚打结束后，滚打轮再次滚打工件，此时的滚打表面不全是未加工表面，在部分已加工过的表面上也进行滚打，冲击阻力显著减小，工件的变形抗力减小，工件不断旋转，使滚打轮接触到新的工件表面。

2 丝杠冷滚打成形过程的有限元仿真

应用ABAQUS软件对丝杠冷滚打成形过程进行有限元模拟，采用Johnson-Cook 模型(J-C模型)来描述材料的本构关系：

(2)

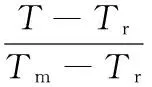
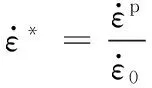
采用紫铜作为毛坯材料， J-C模型参数如表1所示。

表1 紫铜J-C模型参数

选取轴坯材料圆周的六分之一，并对滚打轮的滚打主轴实行简化，只创建滚打轮，并将三个滚轮按120°均布安装于滚打主轴线上，应用ABAQUS软件对丝杠冷滚打进行三维有限元分析，几何模型和有限元模型如图2所示。丝杠滚打局部区域进行网格细化，并选用显式线性3DStress六面体单元C3D8R对工件进行网格划分，最终划分单元数为670 000个。在边界条件定义中，丝杠工件只绕其轴心旋转，同时约束其他五个自由度；滚打轮包含两个运动，即绕参考点的旋转运动和平行于工件轴线的移动；主面为刚度较大的滚打轮表面，从面为工件表面。在较好润滑条件下，冷轧和冷冲挤的摩擦因数在0.1以下，热轧和挤压成形的摩擦因数一般在0.2以下。冷滚打成形中滚打轮径向打入工件，工件产生较大的塑性变形，滑动摩擦占了较大的比例，摩擦因数介于滚动摩擦因数和滑动摩擦因数之间。参考工件所采用紫铜和滚打轮材料接触的摩擦因数，考虑到冷滚打成形时无润滑或润滑效果差的特点，并查阅和分析在润滑剂作用下的具体情况而综合拟定，文献[4]、文献[8]亦证实了摩擦因数的设置与实验结果较相符，因此选取摩擦因数为0.2，摩擦模型选择罚摩擦公式，接触面的法向作用选择硬接触。

图2 丝杠冷滚打几何模型和有限元模型Fig.2 Geometry and finite element models of cold roll-beating

丝杠高速冷滚打成形过程是一个非线性的变化过程，主要是滚打轮高速击打和滚轧工件表面，迫使其短时间内产生较大的塑性变形，最终形成丝杠廓形。图3所示为相同时间间隔内，冷滚打一次时工件径向中间截面的变化情况。

(a)t=0.175 ms (b)t=0.350 ms

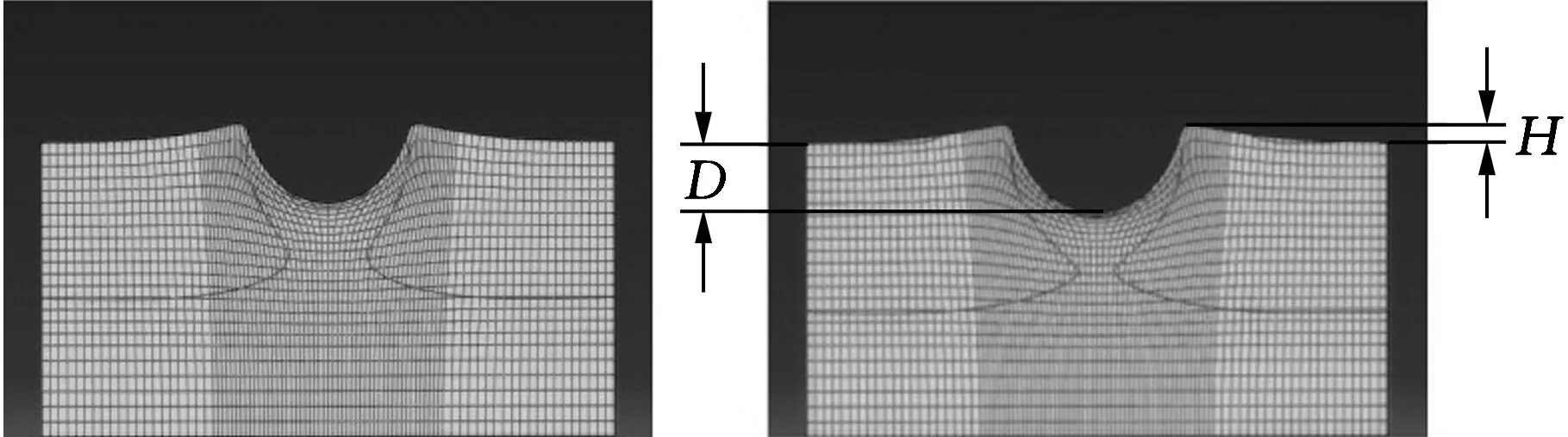
(c)t=0.525 ms (d)t=0.700 ms图3 丝杠冷滚打成形过程中截面形状变化情况Fig.3 Profile section change in the cold roll-beating process

图3a所示为工件在滚打轮刚接触工件表面时的变形情况。材料受滚打轮的作用已发生塑性流动，但是表层外翻量不大，滚打轮冲击到工件表面后引起工件瞬间变形，为后续滚打轮持续推移金属做好准备。由图3b可以看出，经过相同的时间后，工件的廓形变化明显，由于滚打轮打入工件的体积空间增大，根据体积不变原理，这部分体积将向外翻，使图中沿工件轴向(图中左右两侧)的金属在高度和宽度方向发生变化。随后滚打轮继续滚打工件表面，此时工件在径向(图中的竖直方向)进一步被压缩，如图3c所示，与图3b相比，竖直方向的尺寸变化的幅度有所减小，外翻凸起的最高点基本不发生变化，同时金属在滚打轮不断挤压推移的作用下，凸起宽度方向的坡度变缓，说明金属在沿此方向不断充填。图3d所示为滚打轮刚刚离开该截面，工件凹槽由于滚打作用继续被压缩，压缩量明显减小，随着滚打轮与该截面接触作用力的卸载，工件形状尺寸基本稳定，并达到最大滚打深度，图3d中D为最大打入深度，H为外翻凸起最大值。

由图3可以看出，在冷滚打成形过程中，工件形状的变化受滚打轮本身制约，其厚度和半径均影响工件金属流动。滚打出的齿廓形状沿工件径向截面呈对称分布，滚打出的凹槽深度不断增大，但是增大的幅度逐渐减小，外翻凸起的高度逐渐增大，且达到最大值后不再发生变化，只是向水平方向推移，使此方向坡度变缓。总体上，成形过程工件形状的变化主要发生在高度方向，其次是宽度方向，工件受到滚打轮的滚压、击打与挤压复合作用，从而形成所需的齿廓。

3 丝杠冷滚打成形工艺参数的多元回归分析

丝杠冷滚打仿真结果可以分析发现，工件廓形的凸起最大值H、最大打入深度D与打入量f、滚轮厚度h、滚轮转速nr和工件转速nw有一定的相关关系。对上述四个因素进行正交试验，每个因素选定为3个水平。滚打轮仿真材料选用GCr15，考虑该材料对紫铜单次滚打最大深度，对打入量f取三个水平：0.5 mm、1.0 mm、1.5 mm。针对常用丝杠的螺距宽度，选取滚打轮厚度h的三个水平：2.0 mm、2.5 mm、3.0 mm。在机床主轴的回转带动下，当滚打轮接触工件时，摩擦力会使得滚打轮自身高速回转，滚打轮与工件间的摩擦以及主轴转速均影响滚打轮转速nr，综合考虑，选择滚打轮转速nr的三个水平：1000 r/min、2000 r/min、3000 r/min。为提高丝杠表面质量，需要选取合适的工件转速nw，以保证成形的均匀连续性，上述因素与滚打轮的滚打频率以及目标件的尺寸要求相关，以往研究表明，工件转速在35 r/min内可以保证成形的连续性，为此选择工件转速nw的三个水平：10 r/min、20 r/min、30 r/min。

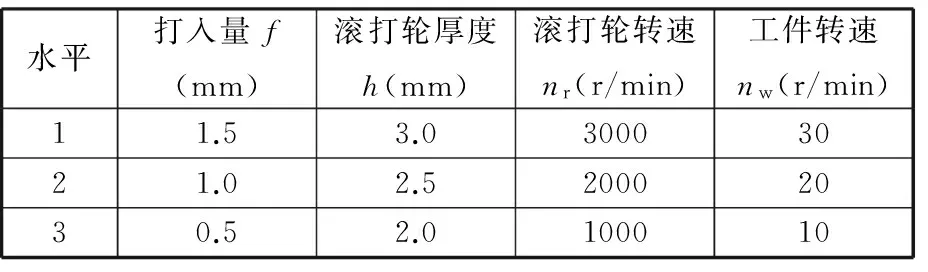
表2 正交水平表

3.1 多元回归模型的建立与求解

设凸起最大值与各工艺参数间的回归模型为

(3)

式中，n1、n2、n3、n4分别为H对f、h、nr、nw的偏回归系数，其大小表示各变量对变量H的影响程度;c1为常数项。

模拟结果的正交试验值如表3所示。

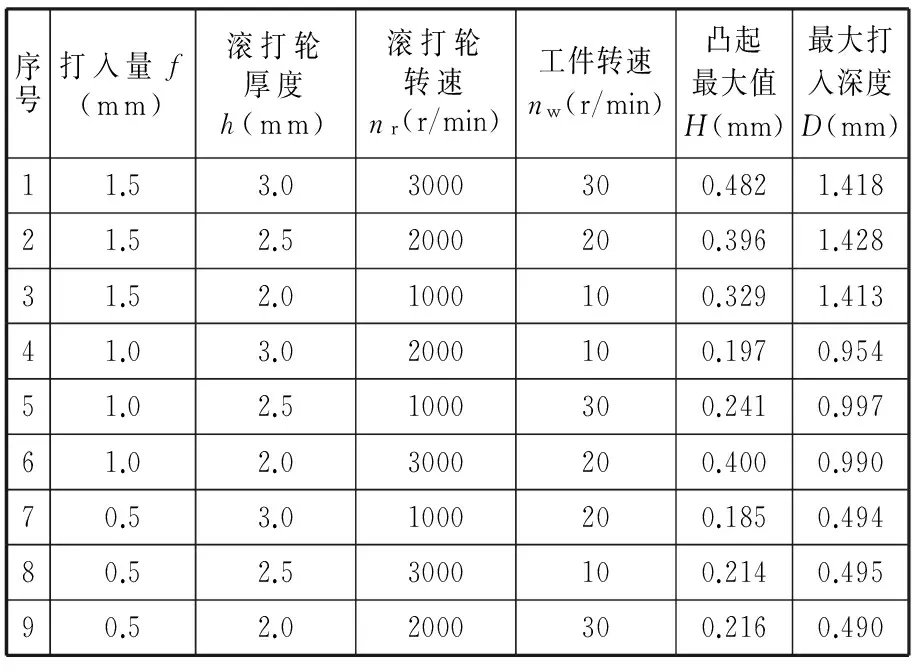
表3 正交试验值

对凸起最大值H和最大打入深度D的回归模型的两端分别取对数，可以得

lnH=lnc1+n1lnf+n2lnh+n3lnnr+n4lnnw

(4)

lnD=lnc2+m1lnf+m2lnh+m3lnnr+m4lnnw

肖红卫等［8］研究的40个基因里面，其基因的产物一起构成了猪繁殖性状相关的蛋白互作网络，这些基因在153个表型中起作用，具体见表2。

(5)

式中，m1、m2、m3、m4分别为D对f、h、nr、nw的偏回归系数，其大小表示各变量对变量D的影响程度;c2为常数项。

令lnf=X1，lnh=X2，lnnr=X3，lnnw=X4，此时所选模型可写为如下形式：

Y=B0+B1X1+B2X2+B3X3+B4X4

(6)

B0=lnc2

式中，B1～B4为对应的回归系数；B0为常数项。

经矩阵计算得

Y=-3.5938+0.5811X1-0.3993X2+
0.2872X3+0.1992X4

(7)

则其对应回归模型为

(8)

f∈(0.5,1.5)h∈(2,3)

nr∈(1000,3000)nw∈(10,30)

式(8)即为凸起最大值与滚轮厚度h、打入量f、滚打轮转速nr和工件转速nw之间的经验回归方程。

同理，可以得

(9)

f∈(0.5,1.5)h∈(2,3)

nr∈(1000,3000)nw∈(10,30)

式(9)为最大打入深度关于滚轮厚度h、打入量f、滚轮转速nr和工件转速nw之间的经验回归方程。

3.2 多元回归方程的显著性检验

上面的计算可以得到凸起最大值和最大打入深度与滚轮厚度h、打入量f、滚打轮转速nr和工件转速nw之间的非线性回归方程，但回归方程是否能反映各变量间的真实关系，还需要进行显著性检验。一般采用相关系数和方差分析这两种方法进行显著性检验。

3.2.1凸起最大值回归方程的显著性检验

(1)相关系数检验法。相关系数R是反映回归方程效果好坏的重要评价指标，其计算表达式为

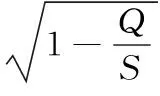
(10)

式中，Q为残差平方和，反映其他因素引起的波动性；S为总偏差平方和，反映变量总波动情况。

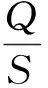
(2)方差分析法。采用F检验进行方差分析。F检验的方差分析结果见表4。

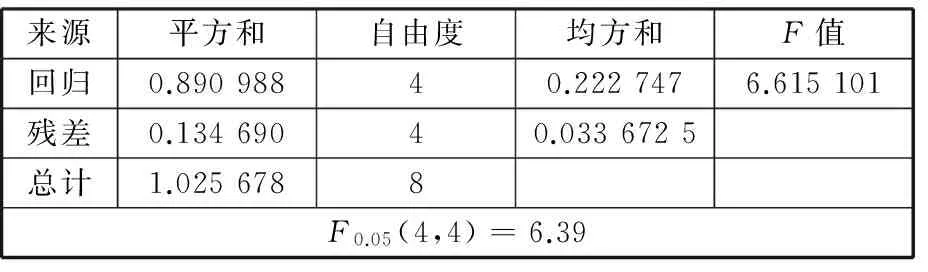
表4 方差分析表

由表4可以看出，当显著水平α=0.05时，F>Fα，回归效果较为显著，因此凸起最大值的回归方程有效。设定不同工艺参数的取值范围，利用回归经验公式可以预测廓形凸起的最大值，为指导工件实际成形过程提供理论依据。

3.2.2打入最深量回归方程的显著性检验

(1)相关系数检验法。按上述方法，经计算，本次回归方程中的相关系数R=0.994 422，表明回归方程具有很高的可靠性，具备参考价值。

(2)方差分析法。采用F检验进行方差分析，结果如表5所示。由表5可以看出，当显著水平α=0.01时，F>Fα，回归效果比较显著，表明最大打入深度的回归方程有效，这对给定滚打轮打入量和预测工件廓形最大打入深度具有一定的实际指导意义，可用于实际成形过程中零件成形精度的控制。

表5 方差分析表

4 试验分析

利用CA6140车床的自制冷滚打设备进行丝杠冷滚打试验，试验所用的滚打轮材料为GCr15，工件材料为紫铜。图4所示为冷滚打试验装置；图5为试验获得的加工试件的一部分，图中的H′为凸起最大值，D′为最大打入深度。

图4 试验装置图Fig.4 Experimental device

图5 试验加工的试件Fig.5 Experimental trial-piece

设定不同工艺参数进行冷滚打试验，利用白光干涉仪测量每组成形丝杠的凸起最大值H′和最大打入深度D′，依据图5的测量方式，取3组等距H′和D′，将其均值作为H′和D′的实测值，并与回归分析计算结果进行比较，如表6所示。可以看出，计算值和实测值之间存在一定误差，其中最大误差值为20%。这主要是由于所设计的冷滚打装置刚性较差，成形精度较低，但是，建立的回归分析模型可在一定程度上对进一步的精确成形提供参考。

表6 回归分析计算值与试验实测值对比表

5 结论

(1)根据丝杠冷滚打成形的基本原理，应用ABAQUS软件建立有限元仿真模型，采用正交试验的方法，对滚打轮厚度、滚打轮打入量、滚打轮转速和工件转速与凸起最大值和最大打入深度的关系进行仿真，对仿真结果进行多元回归分析，建立廓形凸起最大值、最大打入深度与成形工艺参数的多元回归模型，并对建立的回归方程进行显著性检验。

(2)利用自行设计的丝杠滚打装置，进行了冷滚打试验，用白光干涉仪对试件廓形凸起最大值和最大打入深度进行测量，并将测量结果与回归分析结果进行比较，凸起最大值和最大打入深度的变化规律基本相近，证明了所建回归方程的正确性，为丝杠冷滚打的精确成形提供参考。

[1] 王仲仁, 滕步刚, 汤泽军. 塑性加工技术新进展[J]. 中国机械工程, 2009, 20(1): 108-112. WANG Zhongren，TENG Bugang, TANG Zejun. New Development on Technology of Plasticity[J].China Mechanical Engineering, 2009, 20(1): 108-112.

[2] 袁巨龙, 张飞虎, 戴一帆. 超精密加工领域科学技术发展研究[J]. 机械工程学报, 2010, 46(15): 161-177. YUAN Julong，ZHANG Feihu, DAI Yifan. Development Research of Science and Technologies in Ultra-precision[J].Journal of Mechanical Engineering, 2010, 46(15): 161-177.

[3] YANG Mingshun, YUAN Qilong, LI Yan, et al. Deformation Force Simulation of Lead Screw Cold Roll-beating Based on ABAQUS[J]. Procedia Engineering, 2011, 15(1): 5164-5169.

[4] LI Yan, LI Yuxi, YANG Mingshun, et al. Analyzing the Thermal Mechanical Coupling of 40Cr Cold Roll-beating Forming Process Based on the Johnson-Cook Dynamic Constitutive Equation[J]. International Journal of Heat and Technology, 2015, 33(3): 51-58.

[5] 崔凤奎, 朱文娟, 王晓强, 等. 高速冷滚打成形技术研究现状与发展趋势[J]. 河南理工大学学报(自然科学版), 2012, 31(2): 191-195. CUI Fengkui, ZHU Wenjuan, WANG Xiaoqiang, et al. Current Research and Development Trends of High Speed Cold Rolling Technology[J].Journal of Henan Polytechnic University(Natural Science), 2012, 31(2): 191-195.

[6] 张璐, 李言, 杨明顺. 增量成形研究进展[J]. 宇航材料工艺, 2011, 41(6): 32-38. ZHANG Lu, LI Yan, YANG Mingshun. Recent Development of Incremental Forming[J]. Aerospace Materials & Technology, 2011, 41(6): 32-38.

[7] 张璐, 李言, 杨明顺, 等. 丝杠冷滚打成形过程金属流动规律研究[J]. 中国机械工程, 2012, 23(13): 1623-1628. ZHANG Lu, LI Yan, YANG Mingshun, et al. Study on Metal Flowing of Lead Screw Cold Roll-beating Forming[J]. China Mechanical Engineering, 2012, 23(13): 1623-1628.

[8] LI Yuxi, LI Yan, YANG Mingshun, et al. Determination of 40Cr Johnson-Cook Dynamic Constitutive Equation for Cold Roll-beating Forming Process[J]. Chemical Engineering Transactions, 2015, 46(12): 1159-1164.

[9] 李玉玺, 李言, 杨明顺, 等. 滚珠丝杠冷滚打的齿形理论误差研究[J]. 兵工学报, 2015,36(8):1594-1600. LI Yuxi，LI Yan，YANG Mingshun, et al. Investigation of the Tooth Profile Error Based on the Forming Theory of Ball Screw Manufactured by Cold Rolling[J]. Acta Armamentarii, 2015, 36(8): 1594-1600.

[10] 袁启龙, 李言, 杨明顺, 等. 块体材料冷滚打成形变形力研究[J]. 中国机械工程, 2014, 25(2): 251-256. YUAN Qilong, LI Yan, YANG Mingshun, et al. Research on Deforming Force of Slab Cold Roll-beating[J]. China Mechanical Engineering, 2014, 25(2): 251-256.

(编辑胡佳慧)

StudyonShapingParameterControlofLeadScrewColdRoll-Beating

LI Yuxi1LI Yan1CUI Limu1YANG Mingshun1XIAO Jiming1CUI Fengkui2

1.School of Machinery and Precision Instrument Engineering,Xi’an University of Technology,Xi’an,710048 2.School of Mechatronics Engineering,Henan University of Science and Technology,Luoyang,Henan,471003

TG335

10.3969/j.issn.1004-132X.2017.19.019

2016-11-21

国家自然科学基金资助项目(51475366，51475146)；陕西省科技计划资助项目(2016JM5074)；西安理工大学博士创新基金资助项目(310-11202j302)

李玉玺，男，1984年生。西安理工大学机械与精密仪器工程学院博士研究生。主要研究方向为先进制造技术。发表论文10篇。E-mail：lyx841125@126.com。李言(通信作者)，男，1960年生。西安理工大学机械与精密仪器工程学院教授、博士研究生导师。崔莅沐，男，1992年生。西安理工大学机械与精密仪器工程学院硕士研究生。杨明顺，男，1974年生。西安理工大学机械与精密仪器工程学院副教授。肖继明，男，1960年生。西安理工大学机械与精密仪器工程学院教授。崔凤奎，男，1957年生。河南科技大学机电学院教授、博士研究生导师。