装配误差传递建模及其精度可靠性评估

苏 春 黄 漪

东南大学机械工程学院，南京，211189

装配误差传递建模及其精度可靠性评估

苏 春 黄 漪

东南大学机械工程学院，南京，211189

研究了刚体零件的装配误差建模以及装配精度可靠性评估方法。将零件误差分成位置误差和方向误差，并采用误差矢量加以描述。综合考虑尺寸误差和形位误差，将装配过程误差分成零件内误差和配合面误差，给出主动配合面和被动配合面的定义。针对典型配合面类型，分析误差组成及其计算方法。采用位姿变换矩阵法建立装配误差模型，分析误差在零件内部以及配合面间的传递过程，计算装配总误差并据此确定装配误差的概率分布。给出装配精度可靠度的定义，通过仿真获得装配精度的可靠度指标。以某测量平台的装配过程为例，完成装配过程误差分析和装配精度可靠度评估，验证模型的有效性。

零件内误差；配合面误差；位姿变换矩阵；装配误差；装配精度可靠性

Abstract:The modeling of assembly errors and the precision reliability assessments for rigid parts was investigated. The part errors were divided into position errors and orientation errors, and described with part error vectors. Considering the differences between dimensional errors and geometrical errors, the assembly errors were classified into internal errors of parts and joint surface errors. The concepts of active joint surfaces and passive joint surfaces were proposed. The composition of the errors and their calculation methods were proposed according to typical types of joint surfaces. An assembly error model was developed through the approach of pose transformation matrix, after that the assembly error accumulations and propagations were analyzed, and the assembly errors were calculated. The probability distributions of assembly errors were determined on the basis of statistical analyses. The concept of precision reliability was proposed, and simulation approach was adopted to calculate the reliability, which provides basis for the evaluation of assembly precisions. Case study of a measuring platform was provided, the assembly errors and precision reliability were obtained, the effectiveness of the proposed models were verified.

Keywords:internal error of part; joint surface error; pose transformation matrix; assembly error; assembly precision reliability

0 引言

装配是机械产品研制的重要环节。装配精度不足会影响产品的预期功能，装配精度过剩又会增加生产成本,因此，开展装配误差源及其传递规律研究、分析装配精度可靠性，具有重要意义。

误差源分析是开展装配精度分析的前提。刘伟东等[1]研究了装配误差的传递机理，将装配误差分为几何位置偏差、形状偏差和装配位置偏差等。彭和平等[2]基于装配过程中的形位公差分析，建立了二维装配模型。文献[3]将误差源分为工件自身、定位固定装置、夹具的尺寸误差及形位公差等因素。此外，误差建模也是装配精度分析的重要内容。误差建模方法主要有偏差流方法、位姿变换矩阵法、摄动法等。HU等[4]以汽车车身零件的装配为对象，采用偏差流理论分析装配过程中误差的传递机理。文献[5-6]构建了基于误差流分析的多工序加工状态空间模型。LIU[7]分别采用统计过程控制法和误差流方法研究了多工序加工过程的误差传递问题。余治民等[8]利用多体运动学原理和坐标变换方法，分析了零件误差和机床加工精度之间的内在关系。黄勇刚等[9]在位姿变换矩阵的基础上，基于旋量理论建立了机器人误差模型并完成误差计算。基于误差流理论，TANG等[10]提出一种多体系统几何误差模型，研究误差在工序之间的累积。CAO等[11]提出一种基于点的误差传递模型，研究定位误差、机床的几何误差以及工具变形等工件偏差。针对以配合面为关键特征的刚性零部件装配，文献[3，12-13]总结了常见装配结合面类型，并开展了误差建模研究。

现有装配精度模型的构建多针对某特定产品，主要考虑某一类公差或装夹误差等误差源对装配的影响，建模过程具有一定的局限性。对于以配合面形式装配的刚性零部件，有关零件连接方式、结合面误差以及误差传递等问题的研究还有待进一步深入。此外，针对装配误差对装配精度的影响还缺乏可信的评价方法，装配精度模型还有待完善。本文考虑装配过程中各类误差源的影响，建立了误差的统一的描述形式。基于刚性零部件的装配特征，将装配过程误差分成零件内误差和配合面误差，采用位姿误差转换矩阵构建误差传递模型，该模型适用于各类刚性零件的装配。在此基础上，给出装配精度可靠性的定义，用以分析装配目标的精度是否达到预期要求。

1 装配误差分析

在装配过程中，刚性零部件的误差通过配合面累积和传递。本节给出装配过程零件误差的统一表达和以配合面为要素的装配过程的相关定义。

1.1 误差表达

零件误差包括零件沿x轴、y轴、z轴的位置误差和方向误差，可以用误差矢量表示。对于任意一个零件，其误差矢量是由零件上某点d沿各坐标轴的微小移动量以及零件绕各坐标轴的微小转动量组成，可以表示为

(1)

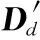
1.2 装配过程的相关定义

配合面是指零件在装配过程中与其他零件有配合关系的面，通常为零件的主要特征面。配合面有平面、圆柱面、锥面、球面等形式[14]，其中平面配合(图1中零件1和零件2的配合)和圆柱面配合(如图1中零件2和零件3的配合)是装配中最为常见的结构形式。

如图1所示，零件按照1→2→3的顺序依次装配。零件1是初始装配零件，称为基准零件；零件3是最终装配零件，称为目标零件；其余零件(如零件2)为中间零件。通常，选取基准零件的非配合平面作为全局基准面，目标零件的工作面为目标面。零件2装配到零件1上，零件1的上表面称为主动配合面，零件2的下表面称为被动配合面。显然，基准零件只存在主动配合面；目标零件只存在被动配合面；中间零件既存在主动配合面，也有被动配合面。

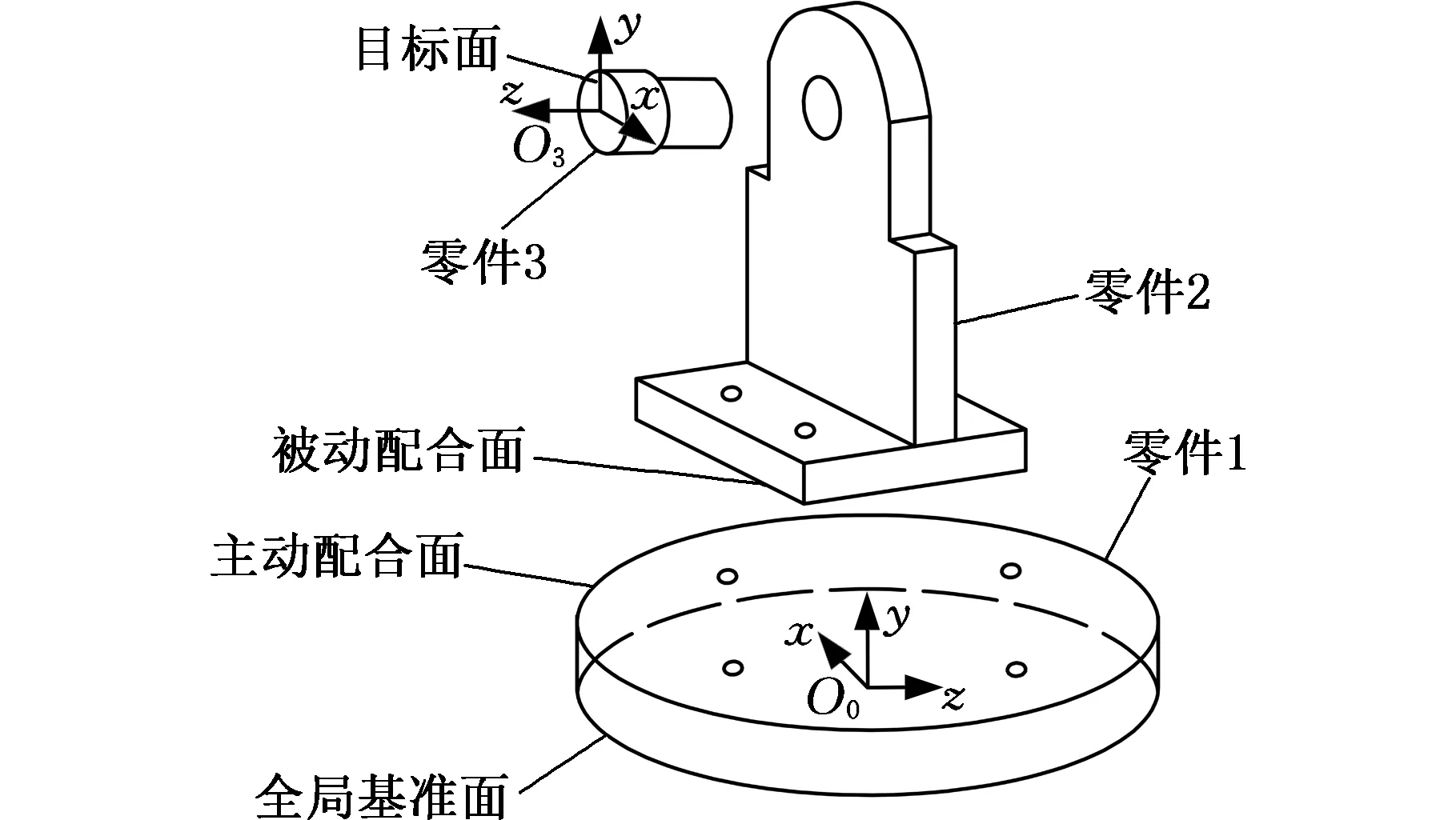
图1 零件装配示意图Fig.1 Schematic diagram of parts assembly

每种误差源都会影响目标零件的装配精度，因此，需对误差源进行分类，并分析不同类型误差与装配精度的关系。本文将误差类型分成零件内误差和配合面误差[1]。零件内误差主要由零件本身决定，本文考虑由加工、制造产生的零件尺寸误差，并用主动配合面上某点的位置误差矢量来表示。相较于零件内误差，配合面误差的组成和计算更为复杂。

1.3 配合面误差

配合面误差受配合面形位误差和连接方式等因素影响。本文将配合面误差分成位置误差和方向误差两部分。其中，位置误差由配合面的连接方式决定，方向误差由配合面的类型决定，并反映在零件的被动配合面上。本文主要研究平面配合和圆柱面配合，分析它们的误差组成及其计算方法。

1.3.1配合面位置误差

通常，对于不可拆卸连接(如焊接、铆接、粘接等)，除非破坏零件结构否则不可拆分，因此，本文将不可拆卸连接的零件视作一个子装配体，建模时将其视作整体加以分析。对于可拆卸连接(如螺纹连接、销连接和键连接等)，位置误差需要考虑配合面位置度误差t和被装配件的平面度误差s，位置误差计算公式为

(2)

式中，θ∈[0,2π]；ΔX1、ΔY1和ΔZ1分别为沿x、y、z方向的位置误差分量。

1.3.2配合面方向误差

(1)平面配合方向误差。通过描述被动装配零件的理想平面与实际平面的偏差量，可以建立平面配合方向误差关系模型。在全局坐标系下，任意零件的理想被动配合面平面方程Z可以表示为

Z=a1X+a2Y+a3

(3)

式中，a1、a2、a3为理想平面方程的表征参数。

通过测量零件几何特征，提取、拟合表面模型，可得到实际的被动配合面平面方程。由最小二乘法可得

(4)

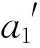
(5)

式中，α1、β1、θ1分别为平面配合的方向误差绕x、y、z轴的误差分量。

(2) 圆柱面配合方向误差。圆柱面配合的位置误差t会使被动装配零件绕x轴和y轴发生微小转动，如图2所示。

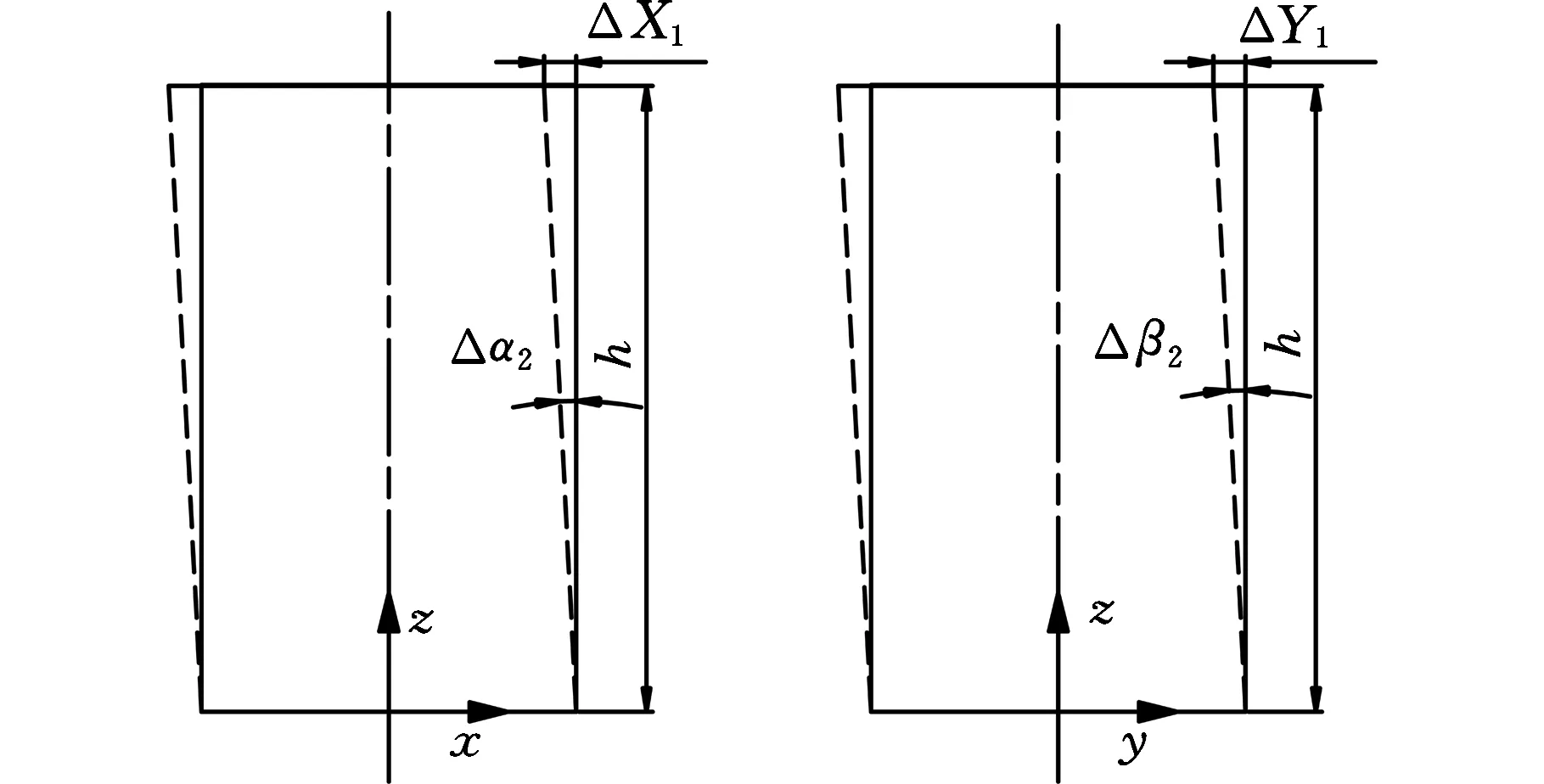
图2 圆柱面配合的方向误差示意图Fig.2 Orientation error of cylindrical surface assembly

根据三角形的几何关系可得

(6)

式中，α2、β2、θ2分别为圆柱面配合引起的绕x、y、z轴的方向误差分量；h为被装配件的高度。

2 装配误差建模及精度可靠性分析

2.1 装配误差建模原理

本文采用位姿误差转换矩阵描述误差在零件内和配合面间的传递。若有N个待装配零件，需要建立2N个坐标系。本文将全局基准坐标系定义为O0，目标坐标系定义为ON，主动配合面上的坐标系分别定义为P1、P2、…、PN-1，被动配合面上的坐标系分别定义为Q1、Q2、…、QN-1。

2.1.1位姿变换原理

零件在不同坐标系下的位姿变换可以由位姿变换矩阵表示。坐标系间的位置变换矩阵

(7)

式中，Trans为平移变换矩阵；a、b、c分别为坐标变换时沿x、y、z方向的移动距离。

坐标系间的角度变换矩阵

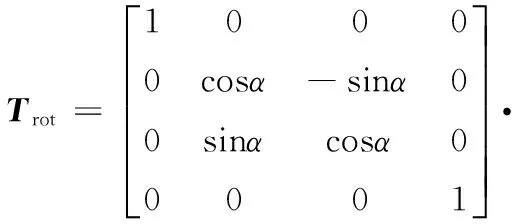
(8)

式中，Trot为旋转变换矩阵；α、β、θ分别为坐标变换时绕x、y、z轴的转动角度。

将式(7)和式(8)合并，可以得到零件在不同坐标系下的理想位姿变换矩阵：

T=TrotTrans

(9)

设存在装配误差，则坐标转换过程会存在沿x、y、z方向的微小移动量Δa、Δb、Δc和绕x、y、z轴的微小转动量Δα、Δβ、Δθ。忽略式(9)中2阶、3阶微小量，可得到位姿误差转换矩阵：

(10)

由此，位姿变换矩阵可以表示为

T′=ΔTT

(11)

2.1.2装配误差传递计算

零件内的误差传递可以描述为尺寸误差从主动配合面到相应被动配合面的传递过程。对于任意第k个中间零件，其主动配合面和被动配合面上的坐标系分别为Pk和Qk-1。

(12)

配合面的误差传递可以描述为误差从第k个零件的被动配合面传递到第k-1个零件的主动配合面。在第k-1个零件的主动配合面建立一个坐标系Pk-1，则有

(13)

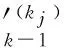
由式(12)和式(13)，并根据位姿变化矩阵的传递关系，可以依次得到目标零件(第N个零件)上点r在坐标系QN-1、PN-1、QN-2、PN-2直至全局坐标系O0的理想坐标矢量和实际坐标矢量，即

(14)

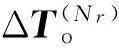
(15)

2.2 装配精度可靠性分析

设装配过程各尺寸误差服从正态分布、形位公差服从瑞利分布，通过计算目标参数的精度可靠度可以判定装配精度。

2.2.1装配精度可靠度的定义

装配精度可靠度是指产品在规定的装配条件下，其实际精度满足设计要求的概率。设计算的实际装配精度为ΔE，目标装配精度为 [ΔE1,ΔE2]。若ΔE1≤ΔE≤ΔE2，则精度符合要求；否则不符合要求。设完成L次(为保证抽样精度，L取足够大)抽样，其中符合要求的次数为M，则装配精度可靠度

R=M/L

(16)

2.2.2装配精度可靠性的计算

在计算装配误差和定义装配精度的基础上，通过模拟装配过程可以得到精度可靠度数据。装配精度可靠度分析流程如图3所示。

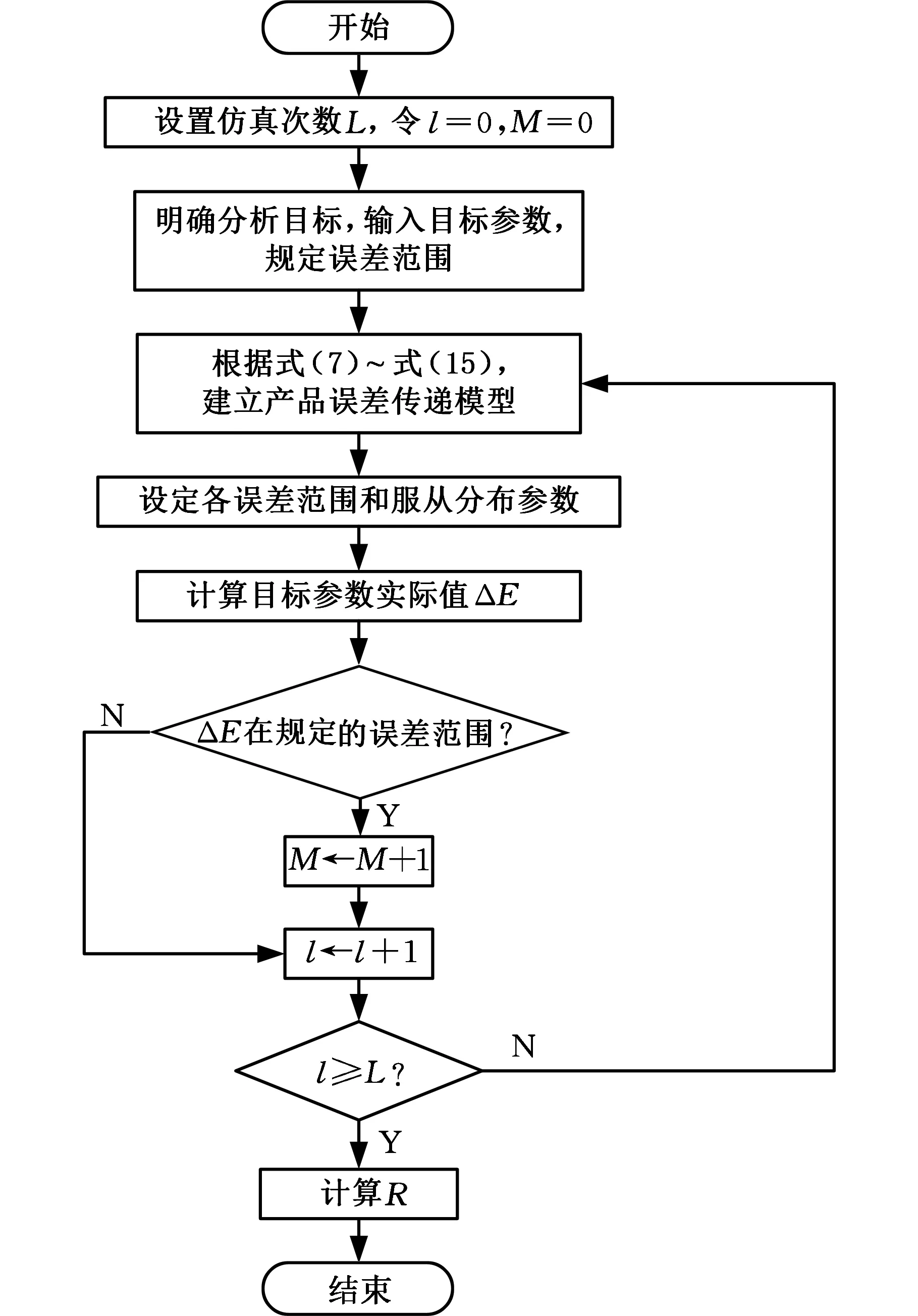
图3 装配精度可靠性分析流程Fig.3 Simulation calculation process

3 案例分析

本节以某型号测量平台机架为例，根据前述建模方法，并按照底座→立柱→头架→工作部分的装配过程进行分析。机架结构和基本尺寸如图4所示，假定非工作状态各零件处于图示位置。各零件的尺寸公差为±0.05 mm，形位公差为0.01 mm。该机架装配精度的目标为：工作部分在各方向位置误差为±0.15 mm的可靠度不小于95%。

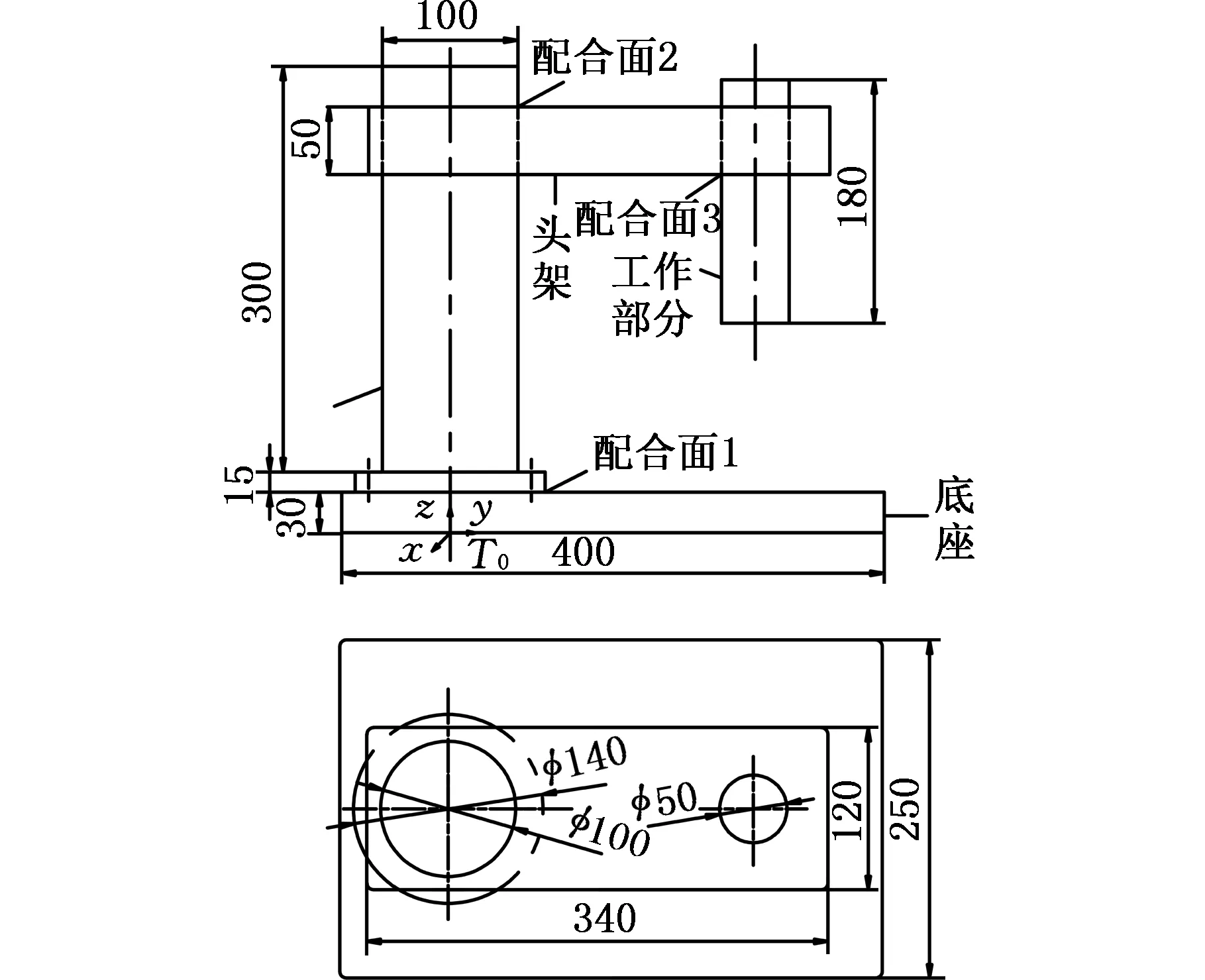
图4 某测量平台机架结构组成Fig.4 A frame model of a measurement platform

以机架结构底座下表面为全局基准面，工作部分的下表面为目标面。其中，配合面1为可拆卸的平面配合，配合面2和配合面3为可拆卸的圆柱面配合，各零件通过配合面形成误差传递累积的装配体。各坐标系的原点坐标如表1所示，各坐标系与全局坐标系T0平行。

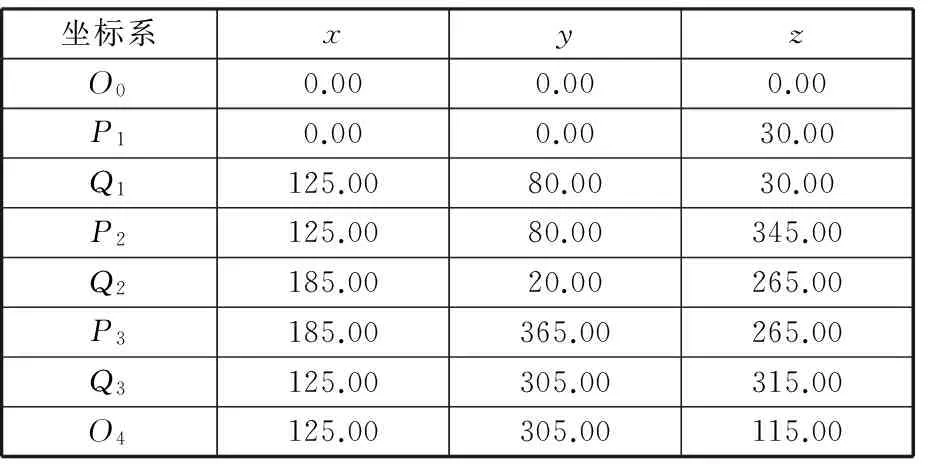
表1 各坐标系相对于全局坐标系的原点坐标

采用MATLAB抽样，得到装配目标在x、y、z方向的位置误差频数分布直方图和误差概率分布图，分别如图5～图7所示。表2为各方向的位置误差的均值和方差。

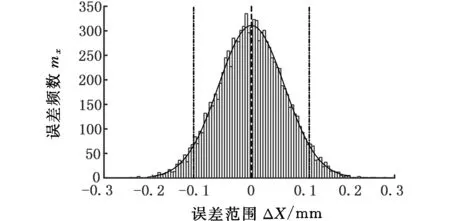
图5 目标面在x向位置误差Fig.5 Position error of target surface in x direction

由图5～图7可知，目标面的位置误差近似服从正态分布。表2中数据表明：z方向的误差大于x、y方向的误差。由测量机架的工作性质可知，z方向是误差敏感方向，且容易产生较大误差。计算结果与实际情况相符。

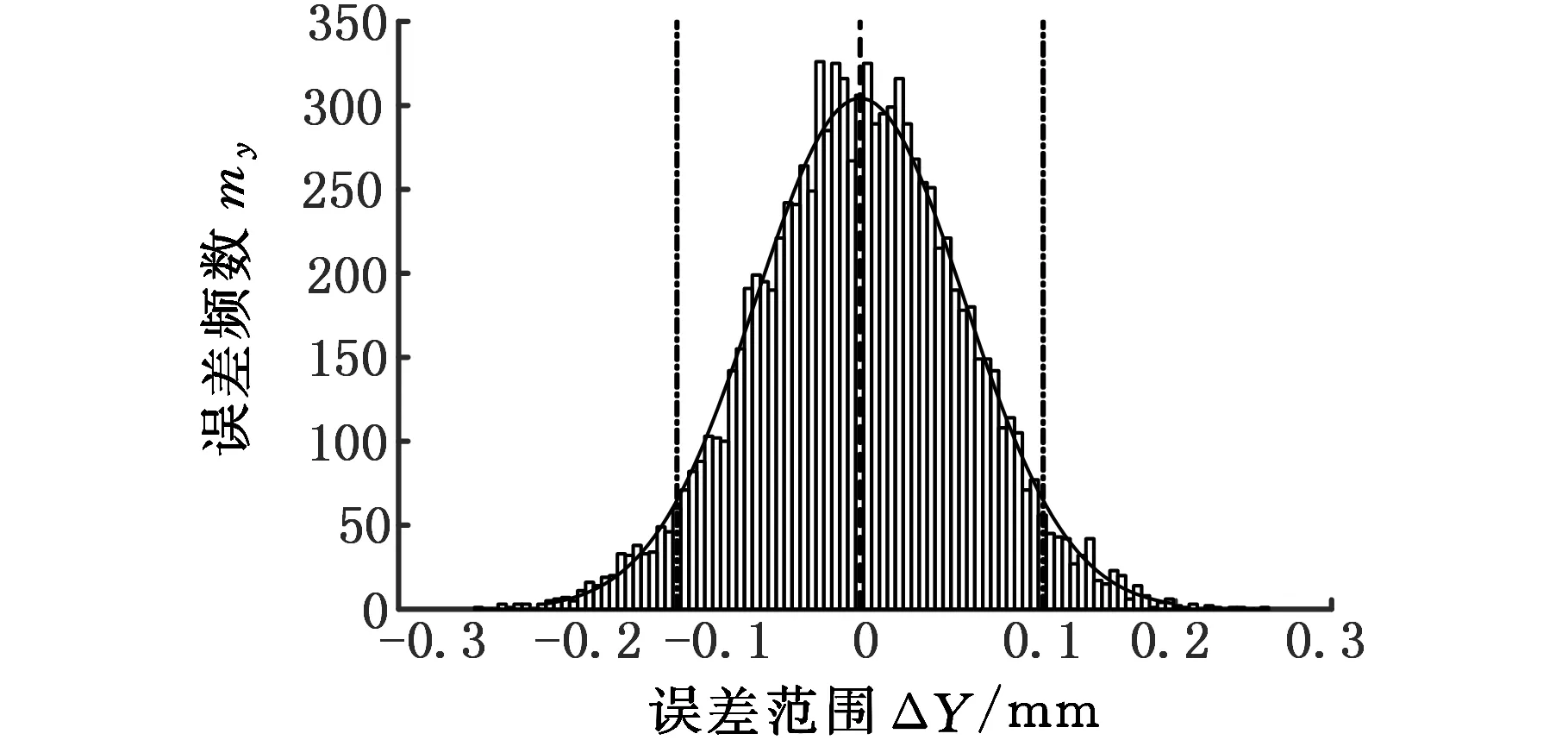
图6 目标面在y向位置误差Fig.6 Position error of target surface in y direction

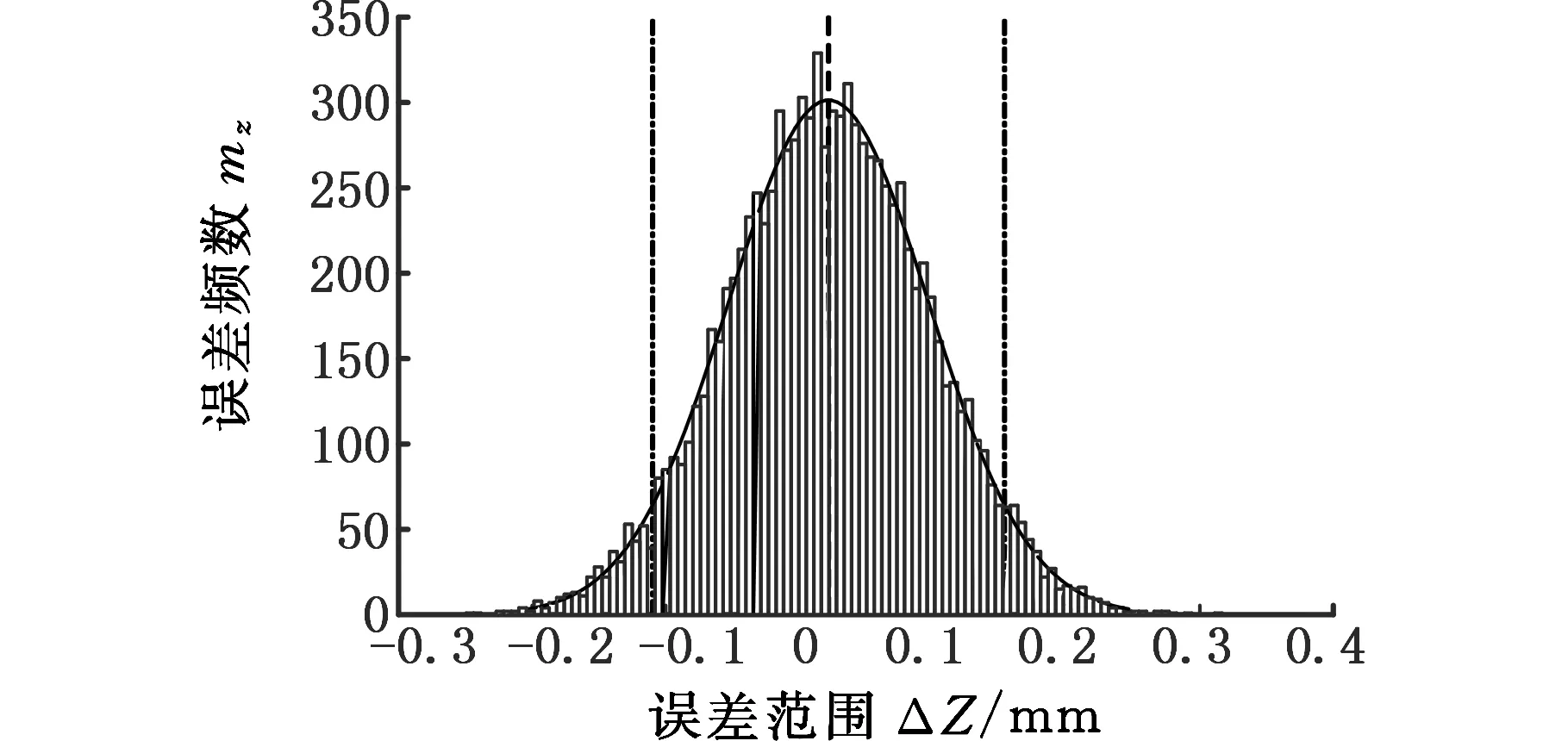
图7 目标面在z向位置误差Fig.7 Position error of target surface in z direction

ΔXΔYΔZ均值(mm)0.0042-0.00420.0211方差0.00410.00450.0057

由图3所示流程开展MATLAB模拟，计算出x、y、z方向的位置误差可靠度分别为97.31%、97.36%和94.37%。x、y方向的位置误差符合装配精度要求，z方向的精度可靠度未达到装配要求。

此外，将各方向的位置误差目标值分别设置为±0.10 mm、±0.15 mm、±0.20 mm，可靠度结果如表3所示。显然，当装配精度目标为±0.10 mm时，各方向位置误差可靠度均不符合要求；当精度目标为±0.15 mm时，x、y方向的位置误差可靠度符合装配精度要求，z方向的位置误差可靠度接近但未达到装配要求；当精度目标为±0.20 mm时，各方向位置误差可靠度均符合要求。

表3 目标面各方向的位置误差可靠度

需要指出的是，不同精度要求实现的难度有所不同，在设置装配精度时需要综合权衡精度目标实现的难易程度、成本等因素，合理确定装配精度。对于装配精度不符合要求的装配体，应采取提高加工精度等措施，以减小零件的制造误差。

4 结论

(1)考虑装配过程中的尺寸公差和形位公差，提出了零件内误差和配合面误差的概念，为装配误差分析提供了新思路。在分析装配误差源的基础上，采用位姿变换矩阵建立装配误差模型，获取装配精度数值。给出装配精度可靠度的定义和数值计算方法，通过计算目标面的误差概率分布，为装配精度可靠性分析提供理论依据。

(2)后续可以开展误差源对装配精度的灵敏性分析研究，并通过优化公差分配，实现装配体精度的改善。

[1] 刘伟东, 宁汝新, 刘检华，等. 机械装配偏差源及其偏差传递机理分析[J]. 机械工程学报, 2012,48(1):156-168. LIU Weidong, NING Ruxin, LIU Jianhua, et al. Mechanism Analysis of Deviation Sourcing and Propagation for Mechanical Assembly [J]. Journal of Mechanical Engineering,2012,48(1):156-168.

[2] 彭和平, 刘晓军. 考虑形位公差的二维装配公差分析[J]. 机械传动,2008,32(3):75-77. PENG Heping, LIU Xiaojun. Two-dimension Assembly Tolerance Analysis Considering Geometric Tolerance[J]. Mechanical Transmission,2008,32(3)：75-77.

[3] ASANTE J N. A Small Displacement Torsor Model for Tolerance Analysis in a Work Piece-fixture Assembly [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture,2009,223(8):1005-1020.

[4] HU S J, KOREN Y. Stream-of-variation Theory for Automotive Body Assembly [J]. CIRP Annals—Manufacturing Technology,1997,46(1):1-6.

[5] DING Y, CEGLAREK D, SHI J. Modeling and Diagnosis of Multistage Manufacturing Processes: Part Ⅰ: State Space Model[C]//Proceedings of the 2000 Annals of Japan/USA Symposium on Flexible Automation. Ann Arbor, MI,2000:23-26.

[6] ZHOU S, HUANG Q, SHI J. State Space Modeling of Dimensional Variation Propagation in Multistage Machining Process Using Differential Motion Vectors [J]. IEEE Transactions on Robotics and Automation,2003,19(2):296-309.

[7] LIU J. Variation Reduction for Multistage Manufacturing Processes: a Comparison Survey of Statistical-process-control VS Stream-of-variation Methodologies [J]. Quality and Reliability Engineering International,2010,26(7):645-661.

[8] 余治民, 刘子建, 艾彦迪, 等. 大型数控龙门导轨磨床几何误差建模与基于可靠性理论的精度分配[J]. 机械工程学报, 2013,49(17):142-151. YU Zhimin, LIU Zijian, AI Yandi, et al. Geometric Error Model and Precision Distribution Based on Reliability Theory for Large CNC Gantry Guide Way Grinder[J]. Journal of Mechanical Engineering,2013,49(17)：142-151.

[9] 黄勇刚, 杜力, 黄茂林. 基于旋量理论的机器人误差建模方法[J]. 哈尔滨工业大学学报, 2010,42(3):484-489. HUANG Yonggang, DU Li, HUANG Maolin. Screw Theory Based Error Modeling Method of Robot Mechanisms[J]. Journal of Harbin Institute of Technology,2010,42(3):484-489.

[10] TANG Hao, DUAN Jian, LAN Shuhuai, et al. A New Geometric Error Modeling Approach for Multi-axis System Based on Stream of Variation Theory [J]. International Journal of Machine Tools and Manufacture,2015,92(1):41-51.

[11] CAO Yanlong, LI Bo, GUAN Jiayan, et al. A Point-based Variation Propagation Model for Multi-pass Machining Process [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2015,229(7):1164-1179.

[12] ANSELMETTI B. Generation of Functional Tolerancing Based on Positioning Features[J]. Computer-aided Design,2006,38(8):902-919.

[13] 吕程, 刘子建. 基于装配定位优先级的并联结合面误差建模[J]. 中国机械工程,2015,26(24):3295-3301. LYU Cheng, LIU Zijian. Parallel Joint Surface Error Modeling Based Assembly Positioning Priority[J]. China Mechanical Engineering,2015,26(24):3295-3301.

[14] 伊国栋, 谭建荣, 张树有, 等. 基于配合面偶的装配约束建模[J]. 浙江大学学报(工学版),2006,40(6):921-926. YI Guodong, TAN Jianrong，ZHANG Shuyou， et al. Assembly Constraint Modeling Based on Mating Surface Couple[J]. Journal of Zhejiang University(Engineering Science),2006,40(6):921-926.

(编辑袁兴玲)

ModelingforAssemblyErrorPropagationsandAssessmentsofAssemblyPrecisionReliability

SU Chun HUANG Yi

School of Mechanical Engineering, Southeast University, Nanjing,211189

TP311.52

10.3969/j.issn.1004-132X.2017.19.014

2016-08-11

国家自然科学基金资助项目(71671035)；国防基础科研计划资助项目(JCKY2016210C007)

苏春，男，1970年生。东南大学机械工程学院教授、博士。主要研究方向为可靠性工程、生产系统工程。发表论文120余篇。E-mail:suchun@seu.edu.cn。黄漪，女，1992年生。东南大学机械工程学院硕士研究生。