基于逐时潮位推求设计水位的统计分布选型研究*

陈呈超， 焦春硕， 翟金金, 董 胜

(中国海洋大学工程学院, 山东 青岛 266100)

基于逐时潮位推求设计水位的统计分布选型研究*

陈呈超， 焦春硕， 翟金金, 董 胜**

(中国海洋大学工程学院, 山东 青岛 266100)

基于沿海长期观测的历时潮位资料，提出了推求设计高(低)水位的传统最大熵分布模型。该分布能够拟合逐时潮位具有双峰的概率密度曲线，计算所得设计高(低)水位，与修改的最大熵分布高潮10%和低潮90%的水位值相比，误差较小。选型的历时潮位曲线分布为港口工程设计水位推算提供了更多的选择，计算精度高，克服了手工方法推算历时潮位设计值的不足，有理论和工程意义。

逐时潮位；设计高水位；设计低水位；理论分布；传统最大熵分布

设计高、低水位是指港口水工建筑物在正常使用条件下的高、低水位。对港口而言，在此水位范围内，设计的最大船舶在各种装卸作业条件下，均可以安全地靠泊并进行装卸作业，同时，在各种设计荷载下，能够满足结构以及地基强度和稳定性的要求。

具有长期潮汐观测资料的港口，确定设计高、低水位有两种方法：一是根据历时潮位资料计算的，一是根据高潮或低潮资料计算的。中国《港口与航道水文规范》规定[1]：对于海岸港和潮汐作用明显的河口港，设计高水位采用高潮累积频率10%的潮位，简称高潮10%；设计低水位采用低潮累积频率90%的潮位，简称低潮90%。如已有历时累积频率统计资料，其设计高(低)潮位也可分别采用历时累积频率1%和98%的潮位。对于汛期潮汐作用不明显的河口港，设计高、低水位分别采用多年历时1%和98%的潮位。在进行潮位累积频率统计时，应有多年的实测潮位资料或至少完整一年逐日每小时的实测潮位资料。

需要指出的是：无论是历时累积频率曲线，还是高潮或低潮累积频率曲线，以往在工程设计中，多采用手工方法进行绘制。2010年董胜和姚艳杰[2]基于逐日高潮和低潮数据，采用修改的最大熵分布(Modified maximum entropy distribution, MMED)推算了海岸港的设计高(低)潮位，计算精度较高，克服了传统方法手绘曲线读取设计值的任意性。而采用MMED绘制历时潮位累积频率曲线，拟合效果不佳，如图1所示。

提出适用于设计高低潮位的随机模型，对于快速、准确计算设计潮位具有重要工程意义。本文首先简介了正态分布(Normal distribution，简称NORM)，对数正态分布(Log-normal distribution, 简称LOGN)，传统最大熵分布(Traditional maximum entropy distribution,简称TMED)，以及修改的最大熵分布，给出未知参数的估计方法。为了与修改最大熵分布进行比较，介绍了K-S统计检验和最小离差平方和的计算流程。再以连云港潮位观测资料为例，探讨了修改最大熵分布拟合历时潮位曲线不佳的原因。最后采用传统最大熵分布计算了设计高低潮位值，并进行了对比，获得有益的结论。

1 潮位的理论分布模型

关于设计潮位理论线型的研究。成果不多。2010年董胜和姚艳杰采用MMED对高潮10%和低潮90%进行了统计分析[2]。2011年董胜等探讨了乘潮潮位的理论分布[3]。为了拟合历时潮位曲线，本文采用正态分布、对数正态分布、传统最大熵分布、修改最大熵分布作为备选分布，通过假设检验和频率离差平方和来确定最优线型。

1.1 正态分布

正态分布的概率密度函数如下：

(1)

式中：μ为随机变量的均值；σ为随机变量的标准差。

1.2 对数正态分布

对数正态分布的概率密度函数如下：

(2)

式中：μy和σy分别是y=lnx的均值和标准差。

1.3 传统最大熵分布

1957年，Jaynes[4]在统计学中提出最大熵原则，“最少偏见的概率分布是这样一种分布，它使熵在已知信息的约束条件下最大化”[5]。即最容易出现的事件其复杂程度或称不确定性程度最大，熵也最大。传统最大熵分布模型可表示为[6]：

(3)

(4)

式中：f(x)为概率密度，是待求解的最大熵分布；H为f(x)的熵，熵最大，即表示在满足已知信息约束下，求出的最大熵分布概率密度函数最客观、合理；式(4)为传统最大熵的约束条件，其中：φi(x),i=0,1,…N为样本的已知函数，且φ0(x)=1；μi为随机变量的各阶原点矩，其中μ0=1；模型阶数根据具体问题确定。

引入Lagrange乘子λi，做目标泛函，即

(5)

要使式(5)中的泛函S达到极值，令S对f(x)的变分为零，即

(6)

解得最大熵的概率密度函数为[7]：

(7)

式中的Lagrange乘子λi可通过下面的非线性方程组求解：

(8)

i=0,1,…,N。

对式(8)做Taylor展开，得到：

Gi(λ)≌Gi(λ0)+(λ-λ0)t[gradGi(λ)]λ=λ0=μi,

n=0,1,…N。

(9)

式(9)可写成矩阵的形式：

Gδ=υ。

(10)

(11)

对海岸工程的历时潮位进行统计分析。令φi(x)表示随机变量潮位x的幂函数，即

φi(x)=xi,i=0,1,…,N,

(12)

则式(7)、(8)、(11)变化为：

(13)

，

(14)

(15)

联立式(13)、(14)和(15)，可求解TMED的参数λ。

1.4 修改最大熵分布

基于最大熵原理，Xu等推导了适用于描述于描述海洋工程环境条件的最大熵分布密度函数[8]。其约束条件如下：

(16)

将式(16)代入Euler方程，并令，α′=-1-λ1，β=λ3，γ=-λ2可得最大熵分布的概率密度函数为[9]：

f(x)=αxγe-βxξ。

(17)

引入位置参数a0，可得改进的最大熵分布

(18)

其中：

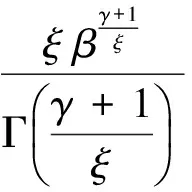
(19)

为了求解式(18)的未知参数，Dong等提出了矩法，经验适线法，以及极大似然法等[10]来估计最大熵分布的未知参数。下面简介极大似然法的求解过程。

最大熵分布函数的似然函数为

(20)

对数似然函数为

(21)

分别对参数β,γ,ξ和a0求偏导，并令其为零，得

(22)

对式(22)中的4个式子进行简化得

(23)

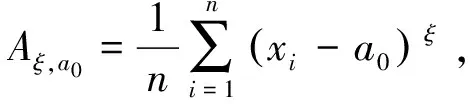
γ+1=βξAξ,a0，

(24)

式(23-b)可变为

(25)

(26)

式(26)化简可得：

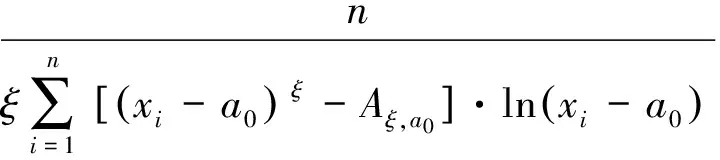
(27)

将式(27)带入式(25)得

(28)

根据式(23-d)可得

(29)

由式(24)可知γ=ξβξ,a0Aξ,a0-1，则上式可变为

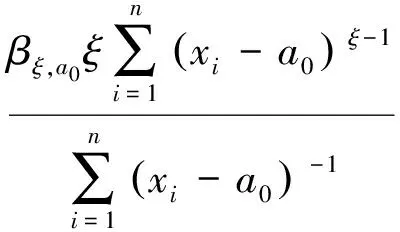
(30)

令

(31)

由于a0∈[0,x(1)]，假设a0值给定，则Aξ,a0仅由ξ确定。将式(27)代入式(28)，可得到ξ的数值解，然后将ξ代入式(27)即可得到β值。将β，ξ和a0代入式(29)，可求得γ值。由于a0是在[0,x(1)]遍历取值，因可以得到很多组(β,γ,ξ,a0)，选取使得式(31)中K值最小的那组(β,γ,ξ,a0)作为一维最大熵分布函数的极大似然参数估计值。

2 分布假设的统计检验

(a)K-S检验

假定样本服从F0(x)的理论分布，采用K-S检验，选取统计量Dn：

(32)

式中：Fn(x)为经验概率分布函数。令

(33)

则K-S检验的统计量Dn为：

(34)

(b)均方根误差法

本文采用均方根误差(Root mean square error, RMSE)法评价各理论分布的拟合优度，其表达式为：

(9)

式中：n为样本容量；Fthe为理论分布的计算值；Femp为经验概率。

3 连云港历时潮位曲线

《港口与航道水文规范》规定[1]，确定设计高(低)潮位时，应有完整的一年或多年的实测潮位资料。本文收集连云港1962—1973年的潮位资料进行历时潮位的统计计算。

(a)连云港设计潮位

收集连云港高潮数据和低潮数据，采用MMED，绘制高潮与低潮累积频率曲线(见图2)，得到连云港高潮10%的值，即设计高水位为518 cm；低潮90%的值，即设计低水位为57 cm。

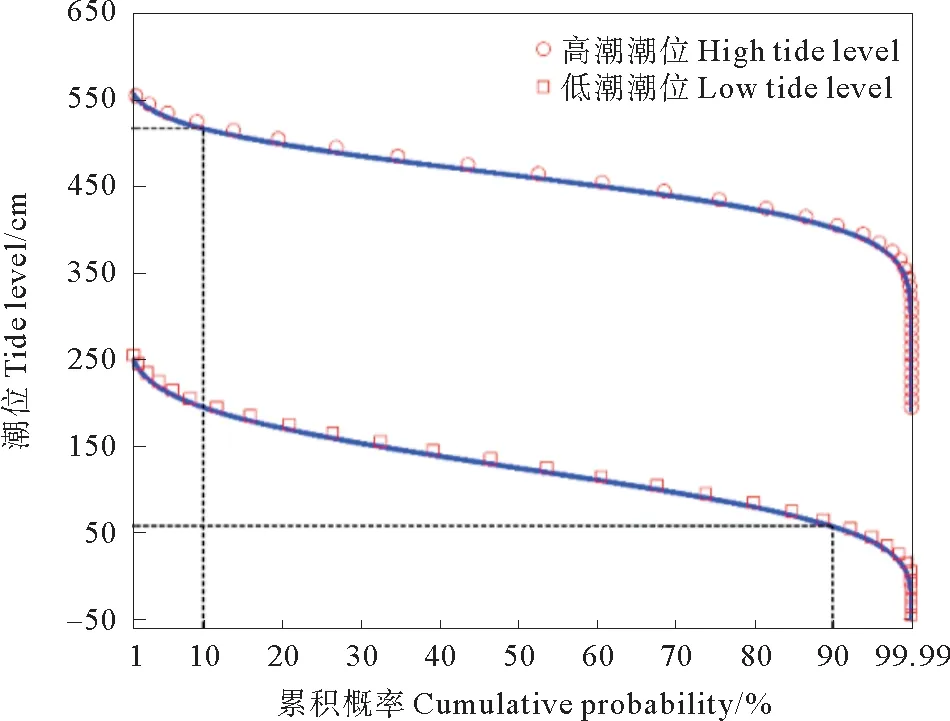
图2 MMED拟合的连云港高(低)潮累积频率曲线Fig.2 High and low cumulative probability curve by MMED for Lianyungang

(b)连云港历时潮位曲线

采用正态分布、对数正态分布、修改最大熵分布、传统最大熵分布，分别绘制历时潮位累积频率曲线(见图3)。各曲线的K-S检验统计量Dn和拟合曲线的频率离差平方和如表1。由不同曲线得到的历时潮位频率1%和98%的值如表2。论文3.1部分，由高潮和低潮累积分布曲线得到设计高水位518 cm，设计低水位57 cm。以此为基准，得到相对误差列入表2。

图3 连云港历时潮位曲线的分布拟合Fig.3 Fitting curve of tide duration at Lianyungang

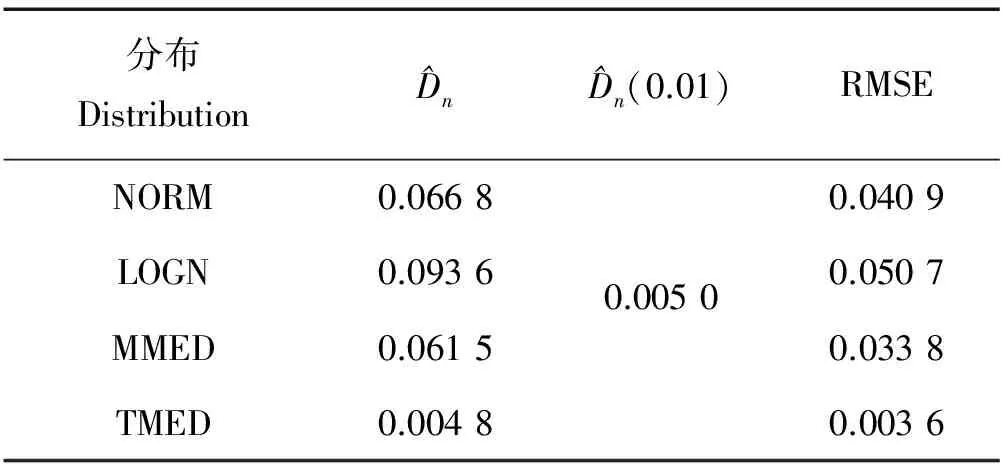
表1 不同分布拟合检验结果Table 1 Fitting test result for different distributions

表2 不同分布所得设计水位值Table 2 Design tide levels by different distributions

(c)计算结果比较分析

根据本文3.1的计算结果，基于高潮潮位资料，修改最大熵分布得到的10%的潮位值，即设计高水位为518 cm。采用低潮潮位资料，改进最大熵分布得到的90%的潮位值，即设计低水位为58 cm。由表2可知，基于历时潮位数据，4种分布中，传统最大熵分布计算的历时1%水位和历时98%水位，与高潮10%和低潮90%的潮位最为接近。

(d)传统最大熵分布概率密度曲线

绘制连云港历时潮位的概率密度直方图(见图4)，在潮位180～190 cm和410～419 cm区间各出现一个密度峰值。绘制4种分布的概率密度曲线如图4。由于正态分布、对数正态分布、修改最大熵分布的概率密度曲线都是单峰的，因此，对应的累积分布曲线拟合程度较差；而传统最大熵分布概率密度是双峰的，对于历时潮位曲线拟合得较优。

图4 连云港历时潮位曲线的概率密度分布Fig.4 Probability density function of tide duration at lianyungang

4 结论

基于历时潮位观测资料，本文选配了统计分布线型。通过计算与对比分析，得到如下结论：

(1)传统最大熵分布适用于港口工程历时潮位设计高(低)水位的推算。

(2)采用传统最大熵分布拟合的历时1%高潮与98%低潮，与修改最大熵分布拟合的高潮10%和低潮90%的潮位精度相当。

(3)修改最大熵分布不适用于历时潮位曲线的拟合，原因是：历时潮位的概率密度曲线为双峰型，而修改最大熵分布是单峰型，采用传统最大熵分布可以克服这一困难。

由于算例有限，传统最大熵分布对其他海岸港口设计潮位的适用性有待做更多的计算验证。

[1] 中华人民共和国交通部. 港口与航道水文规范(JTS145-2015) [S]. 北京: 人民交通出版社, 2015. China Communication Ministry. Code of Hydrology for Harbour and Waterway (JTS145-2015) [S]. Beijing: China Communications Press, 2015.

[2] 董胜, 姚艳杰. 海岸港设计潮位的最大熵分布统计分析 [J]. 港工技术, 2010, 47(5): 6-8. Dong S, Yao Y J. Statistical analysis of design tide levels for coastal ports with maximum entropy distribution [J]. Port Engineering Technology, 2010, 47(5): 6-8.

[3] 董胜, 曹书军, 周冲, 等. 乘潮潮位的理论分布探讨 [J]. 中国海洋大学学报(自然科学版), 2011, 41(7/8): 154-158. Dong S, Cao S J, Zhou C, et al. Study of theoretical distribution for ridable tidal levels [J]. Periodical of Ocean University of China, 2011, 41(7/8): 154-158.

[4] Jaynes E T. Information theory and statistical mechanics[J]. Physical Review, 1957, 106(4): 620-630

[5] 李继清, 张玉山, 王丽萍, 纪昌明. 应用最大熵原理分析水利工程经济效益的风险[J]. 水科学进展, 2003, 14(5): 626-630. Li J Q, Zhang Y S, Wang L P, Ji C M. Application of the maximum entropy principle to risk analysis of economic benefits for water projects [J]. Advances in Water Science, 2003, 14(5): 626-630.

[6] Shanon C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27: 379-423.

[7] Liu F J, Chang T P. Validity analysis of maximum entropy distribution based on different moment constraints for wind energy assessment[J]. Energy, 2011, 36(3): 1820-1826.

[8] Xu Delun, Zhang Jun and Zheng Guizhen. Maximum entropy estimation of n-year extreme wave heights [J]. China Ocean Engineering, 2004, 18(2): 307-314.

[9] Zhang Lizhen, Xu Delun. A new maximum entropy probability function for the surface elevation of nonlinear sea waves [J]. China Ocean Engineering, 2005, 19(4): 637-646.

[10] Dong S, Tao S S, Lei S H, et al. Parameter estimation of the maximum entropy distribution of significant wave height [J]. Journal of Coastal Research, 2013, 29(3): 597-604.

Abstract: With given data of long-term measured tide elevations, there exist two methods to determine design high water (DHW) or design low water (HLW). One is to determine design water (DW) with tide duration curve. The other is to calculate DW with high and low tide elevation data. According to the Code of Hydrology for Sea Harbor, for harbors at sea coast and river estuary with obvious tidal actions, the DHW shall be the water level with 10% of high water accumulation frequency (HW10%) and the HLW shall be the water level with 90% of low water accumulation frequency (LW90%). For coast harbors and estuary harbors with obvious tidal actions, if statistical data of accumulated frequencyies of water level duartion are available, the water levels with 1% and 98% of accumulated frequencies of duration can be used as the DHW and DLW respectively. For esturay harbors without obvious tidal actions during flood preiod, the water levels with 1% and 98% of accumulated frequencies of duration shall be used as the DHW and DLW respectively. For determination of DHW and DLW, the accumulated frequencies of high waters, low waters and tidal water levels with certain duartion shall be satistically calculated with the tide level data obtained from observation for one or several complete years.

No matter with the accumulated frequencies of high waters and low waters, or with the accumulated frequencies of tidal levels with certain duration, the DW are estimated with the plot curve by hand in port engineering design. Based on daily observed data of both high and low tide levels, Dong and Yao adopted Modified Maximum Entropy Distribution (MMED) to calculate design water levels in 2010. The computation accuracy is higher and the shortage of traditional method is overcome. However, the cumulative curve plotted by MMED does not fit tide duration very well.

It makes sense to put forward a suitable statistical distribution to quickly estimate correct design tide levels. Collecting 12-year observed tide elevation data at Lianyungang Port, 4 kinds of distributions, such as Normal distribution, Log-normal distribution, Traditional maximum entropy distribution, and MMED, are candidate theoretical distributions for frequency analysis. Corresponding estimating approaches are given for the unknown parameters of these distributions. The K-S test and Root Mean Square Error are provided for optimal curve selection.Through statistical calculation and result comparison, the conclusions are given as follows:

(1) TMED is suitable to estimate design high and low tide level for coastal port engineering.

(2) The calculation accuracy by TMED is almost the same as that by MMED.

(3) The histogram of tide duration shows its two peaks, but the probability density function of MMED only has one peak. MMED is not suitable to fit tide duration curve. On the contrary, TMED has a 2-peak probability density function, which can fit tide duration curve very well.

Key words: hourlytidal elevation; design high water; design low water; theoretical distribution; traditional maximum entropy distribution

责任编辑 庞 旻

Study of Theoretical Curve Type for Design Water Level Estimation Based on Hourly Tide Elevation

CHEN Cheng-Chao, JIAO Chun-Shuo, ZHAI Jin-Jin, DONG Sheng

(College of Engineering, Ocean University of China, Qingdao 266100，China)

U652.3

A

1672-5174(2017)11-117-07

10.16441/j.cnki.hdxb.20170047

陈呈超， 焦春硕， 翟金金, 等. 基于逐时潮位推求设计水位的统计分布选型研究[J].中国海洋大学学报(自然科学版), 2017, 47(11): 117-123.

CHEN Cheng-Chao, JIAO Chun-Shuo, ZHAI Jin-Jin, et al. Study of theoretical curve type for design water level estimation based on hourly tide elevation[J].Periodical of Ocean University of China, 2017, 47(11): 117-123.

国家自然科学基金项目(51479183) 资助 Supported by the National Natural Science Foundation of China (51479183)

2017-01-25；修改日期：2017-02-27

陈呈超(1977-)，男，博士生。 E-mail: ccc@ouc.edu.cn

** 通讯作者：E-mail: dongsh@ouc.edu.cn