南海北部内孤立波非线性陡斜的数值研究*
2017-10-17张哲恩陈学恩
张哲恩, 陈学恩
(中国海洋大学海洋与大气学院,山东 青岛 266100)
南海北部内孤立波非线性陡斜的数值研究*
张哲恩, 陈学恩**
(中国海洋大学海洋与大气学院,山东 青岛 266100)
基于三维海洋环流模式MITgcm,对非线性陡斜在南海北部内孤立波形成和传播过程中的作用进行了研究,探讨了内孤立波的三维演变过程。研究发现,吕宋海峡处正压潮流激发的斜压潮能射线在其西侧形成强斜压扰动,该扰动在西传过程中受到地形浅化的影响,发生非线性陡斜,波长变小,波形变陡,最终在南海北部陆架坡折处形成大振幅内孤立波,即南海北部的大振幅内孤立波主要是由吕宋海峡西侧的强斜压扰动发展而来,而非来自吕宋海峡巴坦岛附近经潮地相互作用所形成的强波动信号。同时,模式也揭示了a、b波的演变过程,在吕宋海峡西侧约120°E以东的海域,没有发现a、b波,经过西传过程中的非线性陡斜作用,a、b波才演变出来,表明传播过程在a、b波的形成中具有重要意义。
南海北部;数值模拟;内孤立波;非线性陡斜
内孤立波是一种强非线性的内波,其周期通常为10~30 min[1]。卫星遥感和现场观测研究表明南海北部存在频发的大振幅内孤立波[2-13]。在南海深水海盆处曾观测到振幅约170 m,半波宽度约3 km的大振幅内孤立波[10]。Ramp等[8]依据亚洲海国际声学实验(ASIAEX)的现场观测数据,将东沙岛附近的内孤立波分为a波和b波:a波每天同一时间到达其观测站点,头波振幅最大,其后尾波振幅依次减小;b波每天延后1 h到达其观测站点,一般振幅较a波小,且振幅最大的波往往在波列中部。目前普遍认为南海北部的大振幅内孤立波主要来源于吕宋海峡,且已有多种具体的形成机制被提出,如非线性陡斜机制[5,11]和内潮释放机制[14]。
非线性陡斜机制可以概括为三个步骤:首先海水流动受地形阻挡形成波面(Wave Front);接着波面在传播过程中非线性陡化;最后波动在非线性效应和频散效应共同作用下发展成波列[15-16]。Zhao等通过分析卫星遥感数据、东沙岛附近现场观测数据和正压潮流模式数据集,论证了南海北部的内孤立波可以由非线性陡斜机制形成[4-5]。Farmer等根据布设在吕宋海峡及南海海盆的观测站点的观测数据,研究了斜压潮在南海海盆的非线性陡斜过程,进一步佐证了非线性陡斜机制[11]。
内潮释放机制强调了正压潮流在通过吕宋海峡海脊时形成第一模态内波的过程,同时也肯定了传播过程中的非线性陡斜作用在第一模态内波发展成内孤立波这一过程中的重要性,更深入地分析了南海北部内孤立波的生成特点[14]。
由上所述,前人基于卫星遥感和现场观测等对南海北部大振幅内孤立波的生成、传播过程及伴随的非线性陡斜进行了探讨,但卫星遥感还不能较好地反映内波垂向结构,现场观测又局限于少数几个站位,缺乏对南海北部海域内孤立波现象的三维刻画。那么,南海北部大振幅内孤立波在非线性陡斜作用下的三维演变过程是怎样的呢?非线性陡斜过程对a、b波的形成有什么样的影响呢?为此,本文试图从三维数值模拟角度就上述两个问题对南海北部大振幅内孤立波非线性陡斜的具体过程予以研究。
1 模式配置及验证
1.1 模式配置
MITgcm模式通过非静力近似引进了水体垂向加速度导致的非静力压强,从而可以更好地刻画内孤立波。本文研究海域的范围为114°E~129°E,17.8°N~22.5°N,地形数据来自GEBCO_08(见图1)。考虑到内孤立波的水平波长在几百米至十几千米之间,且模拟海域内孤立波主要为西偏北方向传播,将模式东西方向的分辨率设定为500 m,南北方向为1 000 m,时间步长为10 s,满足CFL条件。模式最大水深6 000 m,垂向分层为110层,由表层的10 m每层过渡到底层的400 m每层。模拟时间从2006年6月14日0时刻起,共积分20 d,覆盖时间长度足以分析南海北部内孤立波的演化过程。

图1 模式地形和L1,B2,B1,S7(取自WISE/VANS观测项目)及Y[9]的位置Fig.1 Bathymetric distribution of model domain and selected stations L1, B2, B1, S7 (WISE/VANS project) and Y[9]
模式初始温盐场由WOA13的温盐数据经区域水平平均后赋值(见图2)。在开边界的处理上,模式采用了8分潮潮流驱动(K1、O1、P1、Q1、M2、S2、K2、N2),所使用的调和常数来自俄勒冈大学的TPXO7.2数据集。模式开边界上采用的潮流信号可以很快地传入模式内区并驱动整个模拟海域。本文模式在运行约120 h以后达到稳定状态。在模式内区湍参数化方案的选取上,考虑到本文数值模拟实验是对研究海域在边界正压潮流驱动条件下生成斜压流场的模拟,且内孤立波的耗散、破碎等现象不是本研究的重点,因此采用了KPP方案。
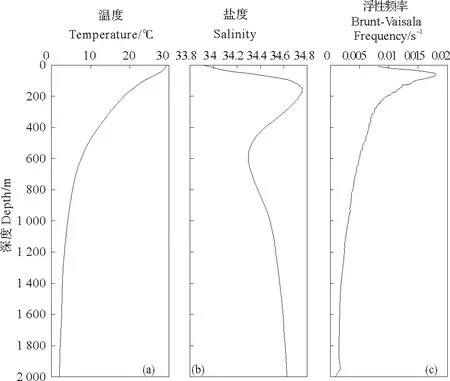
图2 模式初始温度场(a)、盐度场(b)及对应浮性频率(c)的垂向结构Fig.2 Vertical profiles of initial temperature(a), salinity(b) and corresponding buoyancy frequency(c) filed
模式全场数据输出的时间间隔是1 h。考虑到南海北部内孤立波的时间尺度往往在几分钟到几十分钟,在图1的典型选点处输出了1 min时间间隔的模式数据,以能够对南海北部三维斜压场进行时空刻画。
1.2 模式验证
为验证本文模式的可靠性,本文对全模拟海域的潮汐特征进行了验证。在研究海域内,前4大主要天文分潮为M2、K1、O1和S2。因此,本文对静力近似下的斜压模式积分了50 d,取后30 d的海面起伏数据进行调和分析,获得了前4个主要分潮的同潮图(见图3)。
由图3可见,南海北部M2分潮的迟角分布与Fang[19]基于观测数据所绘制的M2分潮迟角分布一致;全日分潮K1和O1在吕宋岛北部存在旋转潮波系统,这一特征也与前人研究吻合[20-22]。同潮图上振幅呈现出波动特征,半日分潮波动条纹之间的间距约为全日分潮的一半,与研究海域内各内潮分潮的水平波长相近,再现了表面潮受到内潮调制的特征[23]。
为进一步验证模式的可靠性,本文计算了纬向正压流速的均方根误差[24]。
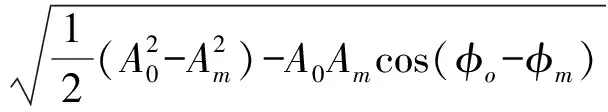
(1)

(色块表示振幅,线表示迟角。Patched color means amplitude, lines mean phase.)
其中:A代表振幅;φ代表迟角,下标m代表TPXO7.2数据,下标0代表模式结果。考虑到吕宋海峡是研究海域内孤立波的主要生成源地,对该区域正压潮流的准确模拟十分重要。从4大主要分潮纬向正压流速的均方根误差分布中(见图4)可以看到,对于吕宋海峡绝大部分海域,4个主要分潮纬向正压流速的均方根误差小于0.06 m·s-1,这说明模式在吕宋海峡处对正压潮流的模拟相对准确。较大的均方根误差主要分布在西海脊北端和东海脊岛屿处,这主要是由于这些地方水深较浅,以及本文模拟并没有考虑波的拖曳效应以及没有经过同化导致的。
上述特征表明,本文建立的数值模式对斜压流场的刻画可信,能够刻画内孤立波的生成和传播过程。
2 讨论
2.1 大振幅内孤立波的演变特征
内波虽然发生在海洋内部密度界面处,但通过引起流场变化造成海表面的辐聚辐散,进而导致海面高度的变化。因此,本文可以通过海面高度梯度的绝对值来追踪内孤立波[25-26]。
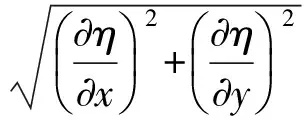
(2)
即,海面高度梯度的绝对值|Δη|在海表面高度η变化越剧烈的地方越大。本文选取了间隔12 h的模式第144、156和168 h的3组模拟数据(见图5),计算海面高度梯度绝对值来刻画内孤立波在研究海域的分布;同时,结合内孤立波传播路径,选取了对应的剖面来刻画内孤立波的垂向结构。图5中剖面中的色块表示斜压流速,即全流速减去正压流速后的成分,黑色实线表示等位温线,用于刻画海洋内部层结的扰动。
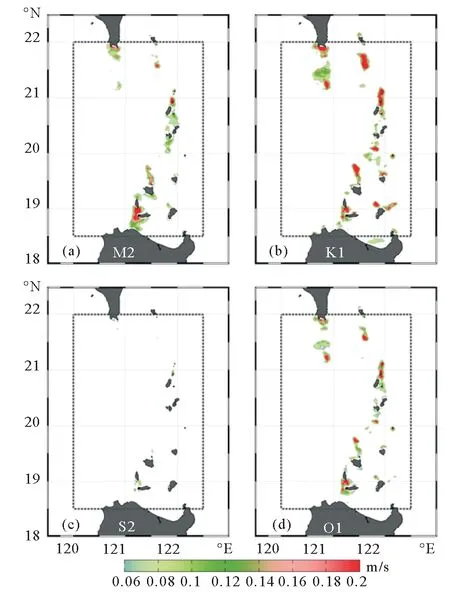
图4 前4大分潮M2(a)、K1(b)、S2(c)和O1(d)纬向正压流速在吕宋海峡的均方根误差分布
在模式第144 h(见图5(a)、(b)),南海北部至少存在三处明显的内波波峰线信号,这里标记南海陆坡处的波峰线为W1,吕宋海峡西侧的波峰线为W2。在W1信号西侧的陆架处,也存在一处较强的短波峰线,但因为这个信号与本文分析关联不大,这里不标记。由图5b可以看到,W2所示的波峰线处具有强烈的斜压扰动,斜压流速要远大于其两侧,等位温线下凹,表现出一个下凹型斜压扰动的结构。在W2的东侧,即其波后,斜压流场结构复杂,甚至存在明显的高模态内波。W1位于水深变化剧烈的南海大陆坡折处,W1处的上层斜压流速与传播方向一致,下层斜压流速与传播方向反向,且等位温线呈现出陡峭的下凹形,表明W1是一个已发育良好的第一模态内孤立波。吕宋海峡东海脊处受驱动潮流和地形作用形成了强烈的斜压扰动,但在吕宋海峡以东并没有观察到显著的内孤立波信号,与南海北部形成了明显的对比。
当模式运行到第156 h(见图5(c)、(d)),W2和W1均传播到了新的位置。W2相比W1传播了更远的距离,表明南海内孤立波在海盆处相比在陆架陆坡处具有更快的传播速度。此时的W2相比12 h前波长变小、波形变陡,表现出更显著的内孤立波特征。即吕宋海峡西侧形成的强斜压扰动在西传过程中,会在非线性效应的作用下逐渐陡斜,从而形成内孤立波。此时的W1仍在浅化过程中,波峰线相比12 h前发生了很大变化,即在地形作用下波峰线不同部分的波速产生了变化,形成了内波的折射现象。
在模式运行的第168 h(见图5(e)、(f)),W2传播到了24 h前W1所处的位置附近,在24 h前W2所处的位置处则形成了新的强斜压扰动W3。此时的W2波长较12 h前进一步减小,波形陡化,同24 h前的W1类似,具有了一模态内孤立波的典型特征。至此,从模式第144~168 h,W2由一个在吕宋海峡西侧受潮地相互作用形成的强斜压扰动信号,在西传的过程中,波长变小,波形变陡,逐渐发育成一个成熟的一模态内孤立波。
前人基于KdV方程的研究表明,在内波波面发展传播的初期,非线性效应的作用要远大于频散效应,波面发生非线性陡斜;当波面陡斜,频散效应也随之增大;当频散效应成长到与非线性效应可比较时,内孤立波也发育成熟[27]。
因此可以预测,新出现的强斜压扰动W3也将会在24 h后到达现在W2所处的位置附近,并经非线性陡斜发育成内孤立波。
上文分析的W1、W2、W3 3个波动信号均在每天的几乎同一时间到达南海北部陆架陆坡处,且振幅较大,波动信号显著,可归类为前人现场观测中所提到的a波。在这3个波动信号之间,例如,图5(a)模式第144 hW1和W2的中间,也存在一个西传的内波信号,依据前人研究中a、b波的特点[8],这个波动极可能是b波。

(色块表示斜压流速(m/s);黑色实线表示等位温线。Patched color means baroclinicvelocity(m/s); Lines mean temperature.)
图5 模式第144 h ((a)、(b))、第156 h((c)、(d))及第168 h((e)、(f))海面高度梯度绝对值分布((a)、(c)、(e))和折线垂向剖面(b、d、f)
Fig.5 Model predicted distributions of sea surface height gradient((a),(c),(e)) and sections along fold-line above ((b),(d),(f)) at the 144th((a),(b))156th((c),(d)) and 168th((e),(f)) model hour
在吕宋海峡以东,在地形和潮流作用下始终存在强斜压扰动,及一些下凹型波动向东传播,但没有明显的内孤立波。可以认为,吕宋海峡处形成的内波在东传过程中,由于水深较深,同时地形的变化难以提供足够的非线性效应来使这些波动陡斜,从而难以形成内孤立波。因此,南海北部不断浅化的地形对非线性陡斜起到了重要作用。这也从侧面论证了在南海北部海域非线性陡斜过程对内孤立波形成演化的重要性。
前文结合了内波信号的水平分布和垂向结构分析了南海北部内孤立波的西向陡斜过程,接下来进一步结合WISE/VANS观测计划在南海北部的站位位置,分析模式在典型选点处的数据以深入刻画上述陡斜过程。
据WISE/VANS观测计划,在吕宋海峡东海脊L1处(20°35′N,121°55′E)直观观测到了强烈的波动信号。从本文模式结果看,L1处(见图6(a))的纬向斜压流速结构和剧烈的等位温线起伏,也表明此处存在强烈且复杂的波动。在大潮期期间,L1处的纬向斜压流速随深度发生2次或多次转向,表明了高模态内波信号的存在。L1位于吕宋海峡东海脊巴坦岛附近,南北两侧有岛屿存在,地形复杂,正压潮流强烈,这些条件使得这个地点可以直接激发出强波动信号。
B2(20°56′N,120°8′E)位于南海海盆,临近西海脊,水深达3 300 m。B2处(见图6(b))具有较强的纬向斜压流速,尤其是在海洋上层,最大斜压流速能达到1 m·s-1。考虑到B2位于西海脊西侧,在海脊地形变化剧烈处所激发的斜压潮能射线刚好能传播到B2处的上层海洋,这可能是造成这里斜压流速能达到1 m·s-1的原因。在大潮期,每隔约24 h,B2处均出现了显著的西向斜压扰动信号。从等位温线上来看,在内潮信号中存在着一些锯齿状的小波动,这可能是一些高频扰动信号,或者是内孤立波发展的初期。在上文的分析中,L1处已经形成了强波动信号,但从B2站点来看,这些波动信号并没有能够传播到B2处,表明南海北部的大振幅内孤立波的主要来源并不在巴坦岛附近。B1(21°21′N,118°35′E)在B2西偏北方向,靠近南海北部大陆坡折,水深约2 500 m。B1处(见图6(c))相比B2处等位温线进一步陡斜,波动时间尺度也进一步减小,表现得更像是一个内孤立波。由于受到传播过程中非线性效应的作用,B1处虽然斜压流速相对B2处较弱,但内孤立波信号更显著。

(其中黑色实线为等位温线。Black lines mean temperature.)
S7(21°36′N,117°16′E)位于南海北部陆架坡折处,水深约335 m。S7处(见图6(d))在大潮期期间内孤立波信号显著,并存在多模态结构。当内孤立波由B1处传到S7处时,已经形成了明显的内孤立波波列结构,波动时间也进一步缩短到几十分钟的量级,即表现为斜压流速、等位温线起伏的变化更加迅速且剧烈。
至此,基于典型选点处的分析表明:在吕宋海峡L1处可以激发强波动信号,但这并不是南海北部内孤立波的主要源地;传到南海陆架陆坡如S7处的内孤立波主要起源于吕宋海峡西侧如B2处的强斜压扰动,这些强扰动信号在西传的过程中,受到非线性效应的作用逐渐陡斜,传到B1处已经形成了较明显的内孤立波结构,在传向S7站位的过程中进一步陡斜,直至形成大振幅、短周期的强非线性内孤立波。
2.2 a、b波
自Ramp等[8]通过分析2000—2001年ASIAEX的观测数据提出a、b波以来,其独特的差异性受到了诸多研究者的关注。Zhao等[5]通过计算一模态线性波相速度反推a、b波的来源,认为a、b波均起源于吕宋海峡巴坦岛处的西向潮流与地形相互作用。Buijsman等[14,28]对此提出了质疑,认为Zhao等可能错误地估计了波传播时间,并提出a、b波的形成与吕宋海峡处的正压潮流东西不对称相关,同时,科氏力、倾斜的等温线以及双海脊效应均能增强a、b波之间的差异。
本文模式在Ramp等人发现a、b波的S7站点[8]成功地再现了a、b波(见图7)。图7是截取放大了图6(d)中方框部分的第28~30个模式日,共72 h的时间序列。由图7可见,S7处的内孤立波可以明显地分成两类,一类振幅较大斜压流速较强,在图7中标记为a1、a2、a3;另一类振幅较小斜压流速较弱,在图7中标记为b1、b2、b3。这两类内孤立波的特征和Ramp等[8]现场观测到的a、b波吻合。即模式中的a波头波表现为一模态下凹型内孤立波,波列后尾随有高模态结构;b波的模态结构则更加复杂,如b1头波表现第一模态,而b3头波则表现为高模态。

(其中黑色实线为等位温线。Black lines mean temperature。)
模式中S7处的大振幅内孤立波均由其东侧的B2、B1站点传播演化而来。值得注意的是,在B2处(见图6(b))一天之内只存在一个强西向扰动信号,而B1处(见图6(c))一天之内存在2个强西向扰动信号。即在B2处并不能够提取到a、b波,而在B1处已可清晰地提取到分离成2个波动的a、b波。从模式结果来看,a、b波在西传的初始阶段(约120°E以东的吕宋海峡西侧)难以分别出来,在之后继续西传中才逐渐可清晰分辨。Zhao和Alford通过整理Yang等在南海陆架坡折处的另一个站点Y(21°2.8′N,117°13.2′E)的观测数据,发现这里一天之内的2个内孤立波波列根据振幅及斜压流速大小也可以分为两类,实际上就是a、b波,但这两类波的时间间隔并不是24和25 h[5,9]。这表明以到达时间来区分a、b波这一方法可能在S7以外的站点并不可行,也暗示我们a、b波的特征在传播过程中存在变化。本文模式结果表明a、b波的特征,如振幅大小、模态结构等,均只有在受到传播过程中的非线性陡斜效应后才清晰可见,因此,传播过程中的非线性陡斜可能是形成a、b波的主要原因。
综上所述,本文的研究揭示在吕宋海峡西侧形成的强斜压扰动信号在西传中经非线性陡斜形成内孤立波,这些内孤立波根据振幅大小、斜压流速大小可以明显地分成两类波,这两类波与前人所说的a、b波相似。前人的研究多认为,a、b波在吕宋海峡处存在不同生成机制[5,8,14,28]。本文的研究则表明,在吕宋海峡西侧如B2处并未能提取到a、b波;当B2处形成的强斜压扰动在西传过程中受非线性作用发生陡斜,a、b波才得以逐渐演变出来,并在南海北部陆架坡折处被前人所观测到。也就是说,传播过程中的非线性陡斜是a、b波形成的主要原因。
3 结语
本文基于三维环流模式MITgcm,在真实地形和8分潮潮流驱动的条件下,对南海北部斜压流场进行了数值模拟,讨论了非线性陡斜过程在南海北部内孤立波演化过程中的作用。研究表明,吕宋海峡巴坦岛附近可以直接激发强波动信号,但这些波动信号并不是南海北部陆架陆坡处大振幅内孤立波的主要来源。南海北部的大振幅内孤立波主要源于吕宋海峡西侧受潮地相互作用所形成的强斜压扰动。这些强斜压扰动在西传的过程中,波面在非线性效应作用下发生陡斜,到达南海北部陆架陆坡处时就可以发育成特征显著的第一模态下凹型内孤立波。对比于吕宋海峡东侧传向西太平洋的强斜压扰动并不能形成大振幅内孤立波,可知南海北部西向不断浅化的地形提供了发生非线性陡斜的必要条件。对于a、b波,在吕宋海峡西侧内孤立波形成的初始阶段难以提取到a、b波,只有当吕宋海峡西侧的强斜压扰动在西传过程中经非线性陡斜后,才逐渐演变成特征显著的a、b波。前人对a、b波的研究主要集中于其在吕宋海峡的生成机制,本文则研究了其在南海北部的传播过程特别是非线性陡斜对a、b波形成演化的重要作用。a、b波各自的特征经西传过程中的非线性陡斜作用之后才表现出来,表明非线性陡斜是a、b波形成的主要原因。
致谢:感谢国家超级计算济南中心提供了“神威蓝光”计算机系统的支持。
[1] 蔡树群, 甘子钧. 南海北部孤立子内波的研究进展 [J]. 地球科学进展, 2001, 16(2): 215-219. Cai S Q, Gan Z J. Progress in the study of the internal soliton in the northern South China Sea [J]. Advance in Earth Sciences, 2001, 16(2): 215-219
[2] Fett R, Rabe K. Satellite observation of internal wave refraction in the South China Sea [J]. Geophysical Research Letters, 1977, 4(5): 189-191.
[3] Liu A K, Chang Y S, Hsu M K, et al. Evolution of nonlinear internal waves in the East and South China Sea [J]. Journal of Geophysical Research: Oceans, 1998, 103(C4): 7995-8008.
[4] Zhao Z, Klemas V, Zheng Q, et al. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea [J]. Geophysical Research Letters, 2004, 31: L06302.
[5] Zhao Z, Alford M H. Source and propagation of internal solitary waves in the northeastern South China Sea [J].Journal of Geophysical Research: Oceans, 2006, 111: C11012.
[6] Zheng Q, Susanto R D, Ho C R, et al. Statistical and dynamical analyses of generation mechanisms of solitary internal waves in the northern South China Sea [J]. Journal of Geophysical Research: Oceans, 2007, 112(C3): C03021.
[7] Du T, Tseng Y H, Yan X H. Impacts of tidal currents and Kuroshio intrusion on the generation of nonlinear internal waves in Luzon Strait [J]. Journal of Geophysical Research: Oceans, 2008, 113(C8): C08015.
[8] Ramp S R, Tang T Y, Duda T F, et al. Internal solitons in the northeastern South China Sea PartⅠ: Sources and deep water propagation [J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1157-1181.
[9] Yang Y J, Tang T Y, Chang M H, et al. Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies [J]. IEEE Journal of Oceanic Engineering, 2004, 29(4): 1182-1199.
[10] Klymak J M, Pinkel R, Liu C T, et al. Prototypical solitons in the South China Sea [J]. Geophysical Research Letters, 2006, 33(11): L11067.
[11] Farmer D, Li Q, Park J H. Internal wave observations in the South China Sea: The role of rotation and non-linearity [J]. Atmosphere Ocean, 2009, 47: 267-280.
[12] 吕海滨, 申辉, 何宜军. 2009年夏季东沙群岛附近内孤立波的现场观测 [J]. 海洋科学, 2013, 37(11): 54-58. Lv H B, Shen H, He Y J. Internal solitary waves at the Dongsha Islands obverted in the summer of 2009 [J]. Marine Sciences, 2013, 37(11): 54-58.
[13] 司广成, 于非, 刁新源. 南海北部中尺度涡与内波相遇的特征分析 [J]. 海洋科学, 2014, 38(7): 89-94. Si G C, Yu F, Diao X Y. Characteristics of encounter between a mesoscale eddy and internal waves in the northern South China Sea [J]. Marine Sciences, 2014, 38(7): 89-94.
[14] Buijsman M C, Kanarska Y, McWilliams J. On the generation and evolution of nonlinear internal waves in the South China Sea [J]. Journal of Geophysical Research: Oceans, 2010, 115: C02012.
[15] Haury L R, Briscoe M G, Orr M H. Tidally generated internal wave packets in Massachusetts Bay [J]. Nature, 1979, 278: 312-317.
[16] Helfrich K R, Melville W K. Long nonlinear internal waves [J]. Annual Review of Fluid Mechanic, 2006, 38: 395-425.
[17] Marshall J, Adcroft A, Hill C, et al. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers [J]. Journal of Geophysical Research: Oceans, 1997, 102(C3): 5753-5766.
[18] Adcroft A, Campin J M, Dukiewicz, et al. MITgcm User Manual[M]. [s.1.]: MIT Department of EAPS, 2008.
[19] Fang G H. Tide and tidal current charts for the marginal seas adjacent to China [J]. Chinese Journal of Oceanology and Limnology, 1986, 4(1): 1-16.
[20] Jan S, Lien R C, Ting C H. Numerical study of baroclinic tides in Luzon Strait [J]. Journal of Oceanography, 2008, 64: 789-802.
[21] Zu T T, Gan J P, Erofeeva S Y. Numerical study of the tide and tidal dynamics in the South China Sea [J]. Deep Sea Research PartⅠ: Oceanographic Research Papers, 2008, 55: 137-154.
[22] Li M J, Hou Y J, Li Y L, et al. Energetics and temporal variability of internal tides in Luzon Strait: A nonhydrostatic numerical simulation [J]. Chinese Journal of Oceanography and Limnology, 2012, 30(5): 852-867.
[23] Niwa Y, Hibiya T. Three-dimensional numerical simulation of M2 internal tides in the East China Sea [J]. Journal of Geophysical Research: Oceans, 2004, 109: C04027.
[24] Cummins P F, Oey L Y. Simulation of barotropic and baroclinic tides off northern British Columbia [J].Journal of Physical Oceanography, 1997, 27(5): 762-781.
[25] Zhang Z, Fringer O, Ramp S. Three-dimensional, nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the South China Sea [J]. Journal of Geophysical Research, 2011, 116: C05022.
[26] 迟乐泉. 南海北部内孤立波三维数值模拟 [D]. 青岛: 中国海洋大学, 2014. CHI Le-Quan. A Three-Dimensional Numerical Simulation of Internal Solitary Waves in the Northern South China Sea[D]. Qingdao: Ocean University of China, 2014.
[27] Lee C Y, Beardsley R C. The generation of Long nonlinear internal waves in a weakly stratified shear flow [J]. Journal of Geophysical Research, 1974, 79(3): 453-462.
[28] Buijsman M C, McWilliams J C, Jackson C R. East-west asymmetry in nonlinear internal waves from Luzon Strait [J]. Journal of Geophysical Research: Oceans, 2010, 115: C10057.
Abstract: The three-dimensional process of internal solitary waves nonlinear steepen in the northern South China Sea is investigated by a nonhydrostatic ocean circulation model MITgcm. Model results suggest baroclinic tidal beams inspired by the interaction between barotropic tide and topography force intense perturbation in the western side of the Luzon Strait, then wave signals nonlinear steepen as they travel west, subsequently getting shorter wavelength and steeper waveform, finally forming large amplitude internal solitary waves at the shelf break in the northern South China Sea. Large amplitude solitary waves in the northern South China Sea are mainly developed from strong baroclinic perturbations in the western side of the Luzon Strait, rather than direct inspired strong fluctuations around Batan Island. Model results also successfully reproduce the evolution process of a-waves and b-waves. a-waves and b-waves are indistinctIn the western side of the Luzon Strait(approximately at the of 120°E), but they are obviously distinct after nonlinear steepen in the west travelling, which suggest the propagation is meaningful for forming a-waves and b-waves.
Key words: Northern South China Sea; numerical simulation; internal solitary wave; nonlinear steepen
责任编辑 庞 旻
Numerical Modelling of Internal Solitary Waves Nonlinear Steepen in the Northern South China Sea
ZHANG Zhe-En, CHEN Xue-En
(College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China)
P731.24
A
1672-5174(2017)11-001-08
10.16441/j.cnki.hdxb.20160367
张哲恩,陈学恩.南海北部内孤立波非线性陡斜的数值研究[J].中国海洋大学学报(自然科学版),2017, 47(11): 1-8.
ZHANG Zhe-En, CHEN Xue-En.Numerical modelling of internal solitary waves nonlinear steepen in the Northern South China Sea[J].Periodical of Ocean University of China, 2017, 47(11): 1-8.
国家自然科学基金项目“南海内波的生成、传播及其三维性(41276008)”;泰山学者计划项目资助 Supported by the National Science Foundation of China “Generation and Propagation of Internal Waves in the SCS as well as Its 3-D Characteristics” (41276008);Taishan Scholars Program Project
2016-10-28;
2016-12-08
张哲恩(1991-),男,硕士生,主要从事内波和内潮数值模拟研究。E-mail: zhangzheen@live.com
** 通讯作者:E-mail: xchen@ouc.edu.cn
