海底子母管作用下海床冲刷的试验研究*

潘新颖， 赵恩金， 拾 兵， 于 冬， 黄修筠

(中国海洋大学工程学院，山东 青岛 266100)

海底子母管作用下海床冲刷的试验研究*

潘新颖， 赵恩金， 拾 兵， 于 冬， 黄修筠

(中国海洋大学工程学院，山东 青岛 266100)

子母管作为海洋工程中的新型管线结构，越来越受到重视。本文运用物理试验的方法研究了稳定流中海底子母管对海床局部冲刷的影响。通过控制不同海底子母管间间距，管径及来流流速，分析出了两管间隙比对冲刷坑内冲刷深度的影响，同时，从泥沙起动原理出发，利用流体的连续性特征，推导了与子母管间间隙比、管径及来流流速相关的冲刷坑深度理论公式，该理论公式与试验结果吻合良好，可预测子母管下泥沙的冲刷。通过试验可知，雷诺数及子母管间间隙对冲刷坑深度有较大的影响。在一定雷诺数下，子母管间间隙越小，冲刷坑深度越大，泥沙输移越也越严重。在管线间间隙比不变时，雷诺数增加同样能加强管线下方冲刷。

子母管线；冲刷深度；海流；冲刷机理；试验研究

随着海底管线的广泛应用，子母管作为一种新的海底管线结构，能够降低管道的设计和施工成本，提高海洋油气田开发的经济效益[1]。子母管的大(母)管用于输送原油，小(子)管位于大管的正上方，用于输送一些置换介质(柴油、海水)及控制信号等。子母管结构如图1所示。D为母管直径，d为子管直径，G为两管之间间隙。该管线结构已在渤海海域BZ34-3/5边际油田中有所应用[2]。管线的存在极易造成下部泥沙的冲刷，造成管线悬空，甚至破坏，因此，对海底子母管下方泥沙冲刷研究极其重要。

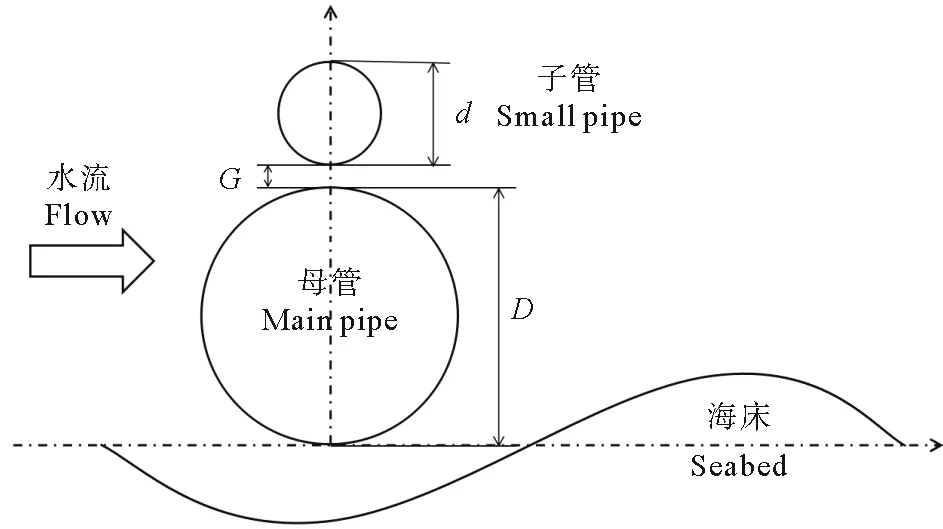
图1 海底子母管的基本结构形式Fig.1 Sketch of submarine piggyback pipeline configuration

海底子母管的结构形式比单一管道的结构复杂，导致子母管周围的水动力特性，流场形态及对海床冲刷影响更为复杂。

目前，国内外对“单一”结构形式管线下的海床局部冲刷已经进行了充分的研究。张芝永等人[3]基于N-S方程和有限体积法，在FLUENT中通过二次开发建立了近床面水平圆柱局部冲刷二维数值模型。刘勇等人[4]对单向恒定流作用下的海底管线冲刷坑内泥沙动水休止角进行了理论分析和试验研究，得出了管线迎流面的动水休止角要略大于背流面的动水休止角并基本呈线性变化规律。Lipeng Yang等人[5]对安装刚性导流板的管线下泥沙冲刷深度进行了计算及试验，他指出雷诺数及导流板高度对冲刷坑深度都有很重要的影响。夏令[6]研究了波浪作用下的泥沙起动及海底管线周围局部冲刷，通过物理试验分析了冲刷发展的物理过程，测量了管道底部的冲刷深度，得到了无因次冲刷深度与KC数之间的一般规律。潘冬子通过波浪水槽实验，研究波浪荷载引起的管线周围局部冲刷机理和形态，探讨了行进波作用下海床局部冲刷的演化规律及平衡冲刷深度与KC数的关系[7]。

然而，对子母管这种新型结构的研究多限制在子母管的水动力特性方面。崔金生等人[8]基于量纲分析的方法，通过模型试验，研究了在稳定海流中子母管涡激振动的情况，指出子母管横向涡激振动具有明显的不对称性。Kalghatgi S G等人[9]对作用在子母管上的水动力强度进行了分析，通过试验指出由于子母管两管的相互影响，作用在子母管上的拖曳力系数比单一结构管线增加50%～100%，对升力系数也有较明显的影响。Zhao Ming等人[10]对恒定流中子母管下的局部冲刷进行了数值模拟，数值模型中两管间的间隙比从0～0.5之间变化，通过分析发现冲刷剖面受间隙比的影响较大，但未对数值模拟结果进行物理验证。马良等人[11]以JZ20-2海底输气管道工程为背景，对JZ20-2的子母管在波流作用下水动力载荷的确定进行了试验研究，分析了子母管水动力系数CD、CM与KC数对管线受力的影响。成小飞等人[12]对波流共同作用下海底子母管线水动力进行了物理模型试验研究，基于Morison方程，采用“等效直径法”分析了流速比Uc/Uw，母管与海床间隙比e/D及子母管间的相对缝隙G/D对海底子母管水动力系数的影响。

当海底子母管铺设在海床面时，能够加剧海床面的冲刷，冲刷坑深度增加，使管线产生滑移造成管线的破坏。之前对子母管的研究着重于管线的受力分析，对子母管下冲刷坑的延展过程研究的却很少。本文通过物理试验的方法，从理论及试验两方面对冲刷过程进行了分析，同时探讨了两管间不同的间隙比(e=G/D，G为两管间间距，D为母管的直径)，子母管管径及来流流速对冲刷的影响，对海底子母管的稳定设计及合理铺放具有非常重要的意义。

1 理论分析

1.1 泥沙起动原理

在恒定流中，管线的两侧存在着压力差，管线前方压力较大，管线尾迹区压力较小，压差使附近海床产生水力梯度，水力梯度越大，管线周围海床泥沙的渗透力越大；当渗透力大于土体浮重并且合力方向向上时，海床便发生管涌，产生渗透破坏[13]。

海底子母管下床面泥沙起动，通过临界希尔兹数确定，其希尔兹数的表达式为

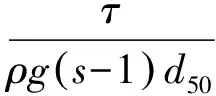
(1)

式中：τ为床面切应力；ρ为水的密度；g为重力加速度；s为泥沙比重；d50为泥沙中值粒径。

海床面上泥沙起动临界希尔兹数为：

(2)

式中：D*=[g(s-1)/v2]1/2，为无量纲泥沙颗粒尺寸。

在有坡度的床面上泥沙临界起动希尔兹数公式[14]，通过如下公式进行修正：

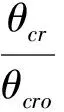
(3)

式中：α是管线冲刷后海床面与水平面的夹角，也称坡角，规定上坡为正角，下坡为负角；φ为泥沙休止角。

产生渗透破坏的临界水力梯度为：

icr=[(ρs/ρw)-1](1-ns)，

(4)

式中：ρs为泥沙密度；ρw为海水密度；ns为沙土孔隙率。

平均单宽体积输沙率q0由下式求得

(5)

式中：s为泥沙比重；θ为泥沙床面希尔兹数；θcr为泥沙临界起动希尔兹数；d50为泥沙中值粒径。

推移质单宽输沙率可表示为：

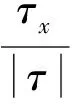
(6)

式中：q0为平面单宽体积输沙率；τ为床面剪应力；τx为床面剪应力x方向分量；经验系数C取值范围为1.5～2.3[15]。

床面变形模型根据输沙平衡规律，海床面高程变化h可用冲淤方程表示：

(7)

式中：p0为床沙孔隙率；qbx为x方向推移质单宽体积输沙率。

1.2 海底子母管下方冲刷平衡后理论分析

冲刷平衡后，子母管线周围流场及冲刷坑情况，如图2所示。

图2 子母管周围流速分布Fig.2 The velocity distribution around piggyback pipeline

冲刷稳定时，将冲刷坑最深点床面上，某高度处沿床面方向的流速定义为“冲止流速”。本文所讨论的冲刷为清水冲刷，且上游无泥沙补给的情况，因此，冲刷稳定时坑内泥沙将处于静止状态，根据力学平衡原理，颗粒所受的升力FL、水下重力Ws、拖曳力FD及摩擦阻力Rf间存在着平衡关系[5]。由此得出，摩擦阻力与重力沿床面分力之和等于推移力，可推出冲止流速为：

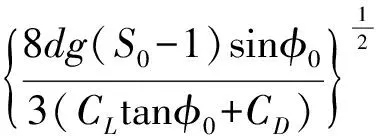
(8)

式中：S0为泥沙容重与水容重的比值(S0=(ρs/ρ)；ρs为泥沙颗粒的比重；ρs为水的比重；g为重力加速度；d为泥沙颗粒平均粒径；φ0为泥沙的动水休止角，其受结构物影响，并随管径、子母管间隙比及来流流速的变化而变化；CL为升力系数，爱因斯坦根据埃尔-萨姆尼的试验成果，发现距理论床面0.35d处的流速对应的CL为常数可取为0.178，CD为推移力系数，当试验条件为紊流时可取0.45[16]。

根据之前研究发现[5]管道冲刷达到稳定后，冲刷坑内流速呈指数分布(见图2)，因受床面和管道边壁的共同影响，最大流速出现在距床面3hb/4处(hb为冲刷坑深度)，则冲刷坑底端至水平海床面3hb/4间的距离为y，流速u(y)可以表达为：

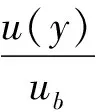
(9)

同时，3hb/4处至管壁处流速u′(y)可以表达为：

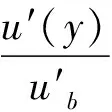
(10)

冲刷坑底部流速与冲刷坑底端至水平海床面3hb/4处的流速关系可用下式表示：

(11)

由于子管的存在，能够增大子母管线整体的阻流受力面积，加剧下方海床面的冲刷及泥沙输移，与单一结构管线相比冲刷坑宽度的幅度大于深度，因此子母管下的动水休止角比单一结构管线下动水休止角小。同时，因受床面和管道边壁的共同影响，根据Yang等人及本试验结果发现冲刷坑内最大流速在冲刷坑最低端到正常海床面深度的3/4处，管道迎流面上驻点的高度随子管与母管之间的间隙G的不同及管径的变化(母管管径为D，子管管径为d)而变化，其表达式为h=(D+de-G)/2。

断面A-A上床面至h处的流速分布可写为：

(12)

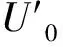
(13)

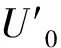
利用流体连续性条件，则有：

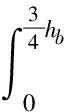
(14)

将式(9)～(13)带入式(14)中，得出子母管下冲刷坑深度的计算公式为：

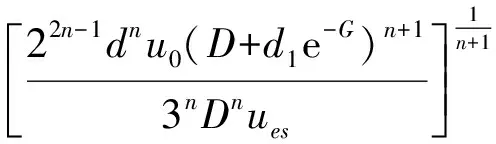
(15)

2 物理试验及分析

本试验在中国海洋大学工程学院河流工程实验室波流环形水槽中进行的，试验物理模型如图3所示。

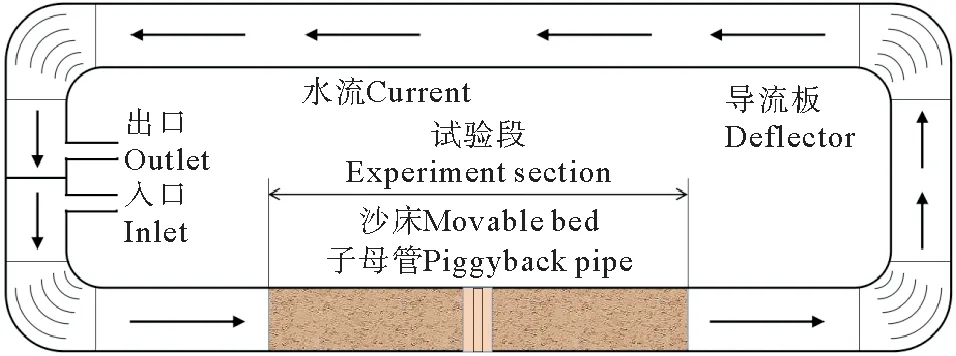
图3 物理试验装置Fig.3 Experiment arrangement

水槽长25.0 m，宽0.5 m，深0.6 m，水槽中央填有非均匀沙，用来模拟沙质海床，沙床高0.15 m，长5.0 m。

2.1 试验参数及步骤

试验主要测量了子母管与床面无间隙比时，不同管径、流速及两管间间隙比对冲刷坑内的流速分布、冲刷深度的影响。管道模型长度为0.5 m，母管外径分别为0.08、0.10、0.12 m，根据工程实际运用[2]，子母管径比一般为0.358，对应的子管外径分别为0.03、0.035、0.04 m。试验中子母管间隙比分别设置为0、0.25、0.5。试验水温为15℃，运动黏滞系数为1.120 1×10-6m/s2。试验水深为Ho=0.4 m，管道上游距床面D/2高度处的来流流速分别为0.24、0.3、0.4 m/s，泥沙中值粒径d50为0.3 mm，孔隙率n为0.4。试验工况及参数如表1所示。

试验值的获取主要集中在动床上，管道上游、管道迎流面及冲刷坑内的流场分布采用ADV(Acoustic Doppler Velocimeter)进行测量，测量精度为±1 mm。试验所用ADV探头为侧向的，测量的是其侧方5 cm处的流速，对测点影响较小，通过流场的试验值可以确定管道上游驻点的高度及流速分布指数。本文中的驻点高度即：管道迎流面上流速为零的点与床面间的高度，其可由管道迎流面的断面流速分布确定。冲刷稳定后，将水槽内水完全排出，采用精度为0.1 mm的测针对冲刷坑的断面进行测量，ADV及测针均垂直固定于水槽上方的数据采集车上，其可沿水槽自由运动，方便取值。

表1 试验工况及参数Table 1 Experiment cases and parameters

2.2 试验结果分析

2.2.1 冲刷现象描述 当水流速度增加到一定值时，管线下方的泥沙渗透力大于泥沙颗粒重力，海床开始出现管涌现象，随着时间和流速的增大，管道底部海床出现一处或几处泥沙输移后产生冲刷间隙，同时，间隙沿着管道轴线方向发展并形成一个冲刷坑。管道悬空主要是由于管线两侧的压力差使沙床内产生渗透力造成泥沙输移[17-19]。当子母管与沙床间的间隙很小时，间隙内的流速是来流流速的数倍，增大了床面的剪切力，造成输沙率增加。当冲刷坑深度及宽度达到一定值后，床面的冲刷坑形态基本不再发生变化，此时，为平衡冲刷阶段，不再出现泥沙输移的情况。

2.2.2 冲刷结果分析 冲刷稳定后冲刷坑的状态取决于子母管管径、子母管管间隙及来流流速，图4给出了不同流速下冲刷坑的几种形态。

在试验中，试验管线采用有机透明玻璃管，为了能看清子母管及冲刷状态，在管内设置了白色泡沫板，而管壁仍为透明状态并且存在一定厚度，因此，在拍摄照片，间隙为0时，如同存在间隙，而试验时两管间并未有间隙存在。试验结果显示：在相同子母管管径及间隙比下，管道下方冲刷坑的深度及宽度随来流流速的增加显著增大，如图4(a)，(b)所示。在相同来流流速及相同管径下，冲刷坑的深度及宽度随着子母管间间隙的增大而减小，如图4(a)，(c)，(e)所示。在相同情况下，冲刷坑的深度及宽度随着管径的增大而增加，并且冲刷坑的最深点出现向下游偏移的趋势。动水休止角与冲止流速和冲刷坑深度的变化规律相反，随着子母管间间隙及流速的增大而减小，并且最终趋于稳定。通过照片对比可知，子母管间间隙对冲刷坑有较大影响，间隙比越小，泥沙冲刷的越剧烈，泥沙输移程度越明显。

图4 不同流速及间隙比下冲刷坑状态(D=0.01m)Fig.4 Experimental photos of the scour around the piggyback pipe for D=10cm

2.2.3 公式参数的确定 通过拟合试验数据的方法确定冲刷坑深度公式中的参数。图5为泥沙休止角与沙粒雷诺数的关系曲线。

通过分析试验数据发现，当管线为单一结构及管线与沙床面无间隙时，休止角φ0是仅与沙粒雷诺数有关的系数，沙粒雷诺数定义为Re*=u*ds/v(u*为摩阻流速)。通过试验数据拟合，得到其关系式为：

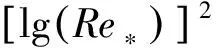
(16)

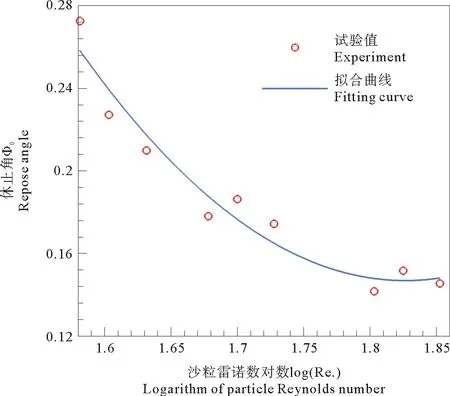
图5 休止角φ0与lg(Re*)的关系式拟合曲线Fig.5 The relationship curve of repose angle and lg(Re*)

当管道为子母管且管线与沙床无间隙时，休止角φ是与子母管间间隙、沙粒雷诺数及管径有关的参数。通过数据分析发现φ可由φ0及系数k表示。其表达式可写为φ/φ0=k=f(G/D)，G为两管间间隙比，D为母管管径，其中，当G趋近于无穷时，相当于单一管线结构状态。拟合曲线如图6所示，则k的关系表达式可写为：

(17)

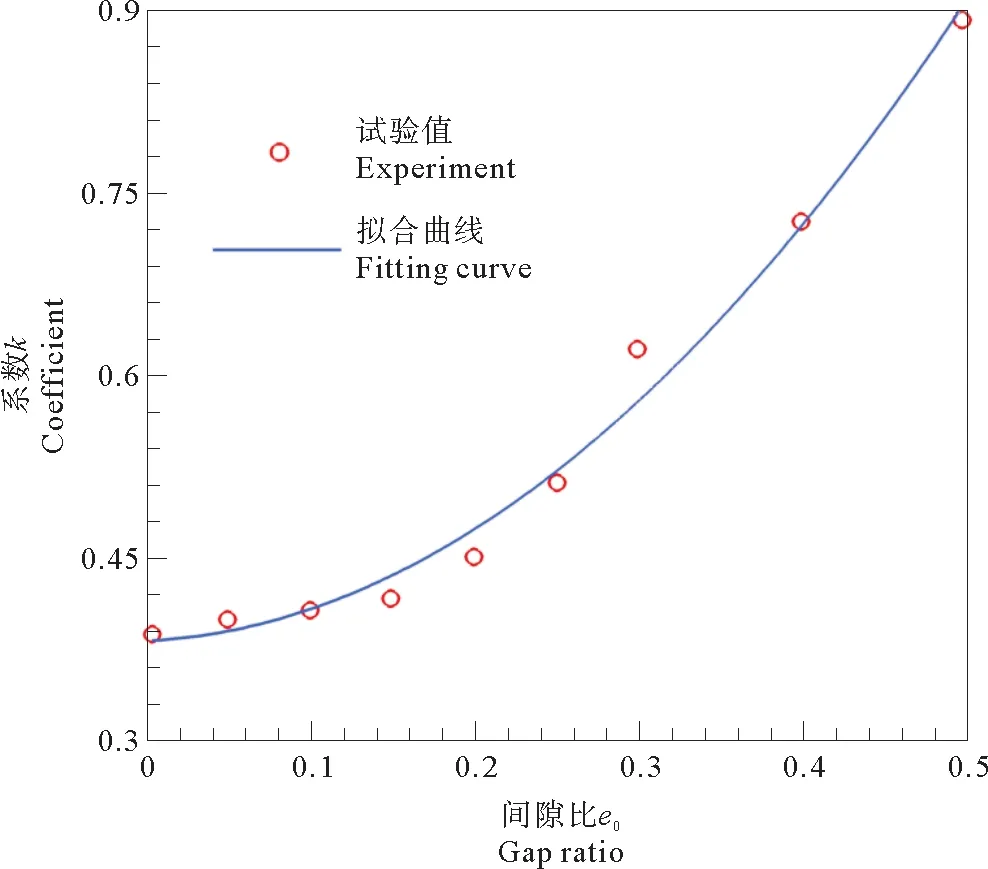
图6 系数k与G/D的关系曲线Fig.6 The relationship curve between k and G/D

指数n是由试验测定的流场数据确定的。试验发现在一定不同条件下(如：相同的子母管间间隙比和管径)，不同来流流速的流场分布规律呈现相同趋势。在此，以图7为例阐述指数的确定方法。图7为子母管线冲刷稳定后，冲刷坑内流速随竖直高度y的变化曲线，y为冲刷坑内距床面的竖直高度；H为水深，u为坑内不同高度处对应的流速。通过图7可知，当流速u0=0.24 m/s时，指数n为1/6时，试验值和拟合曲线吻合良好，当流速u0=0.30 m/s时，指数n为1/4时，两者吻合良好，并且来流流速越小，高度比相对于流速比变化越明显。

图7 不同流速时冲刷坑内流速分布指数nFig.7 The distribution index n in the scour hole

2.3 冲刷坑深度对比

在单一管线及与海床面无间隙的条件下，冲刷深度的计算值中即不存在子管与子母管间间隙，即式中的间隙距离G趋近于无穷，计算值与试验值的对比曲线如图8所示。对于同一管径，深度随流速的增加而增大；对于同一试验条件(如来流流速)，深度随管径的增大而增大。并且Mao[20]的试验数据也用来验证计算公式，结果显示：计算值与试验值相近，公式能反映试验数据的变化规律。

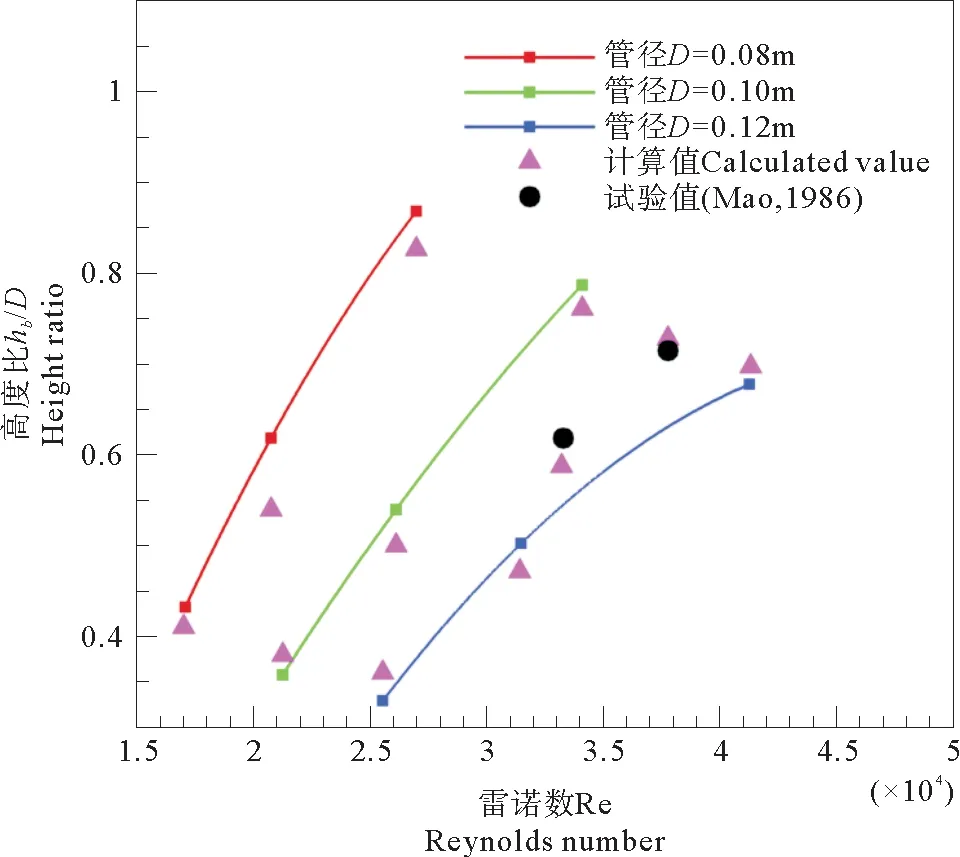
图8 无间隙单一管线计算值与试验值对比曲线Fig.8 The comparison between calculated data and test values

下图为子母管线两管间不同间隙比时，冲刷坑的深度计算值与试验值的对比曲线。由图9可知，冲刷坑深度随着间隙比的减小而增大，随着雷诺数的增加而增大；同一雷诺数条件下，间隙比为0时冲刷坑深度远远大于间隙比为0.5时的冲刷坑深度，来流流速越大这种趋势越明显。

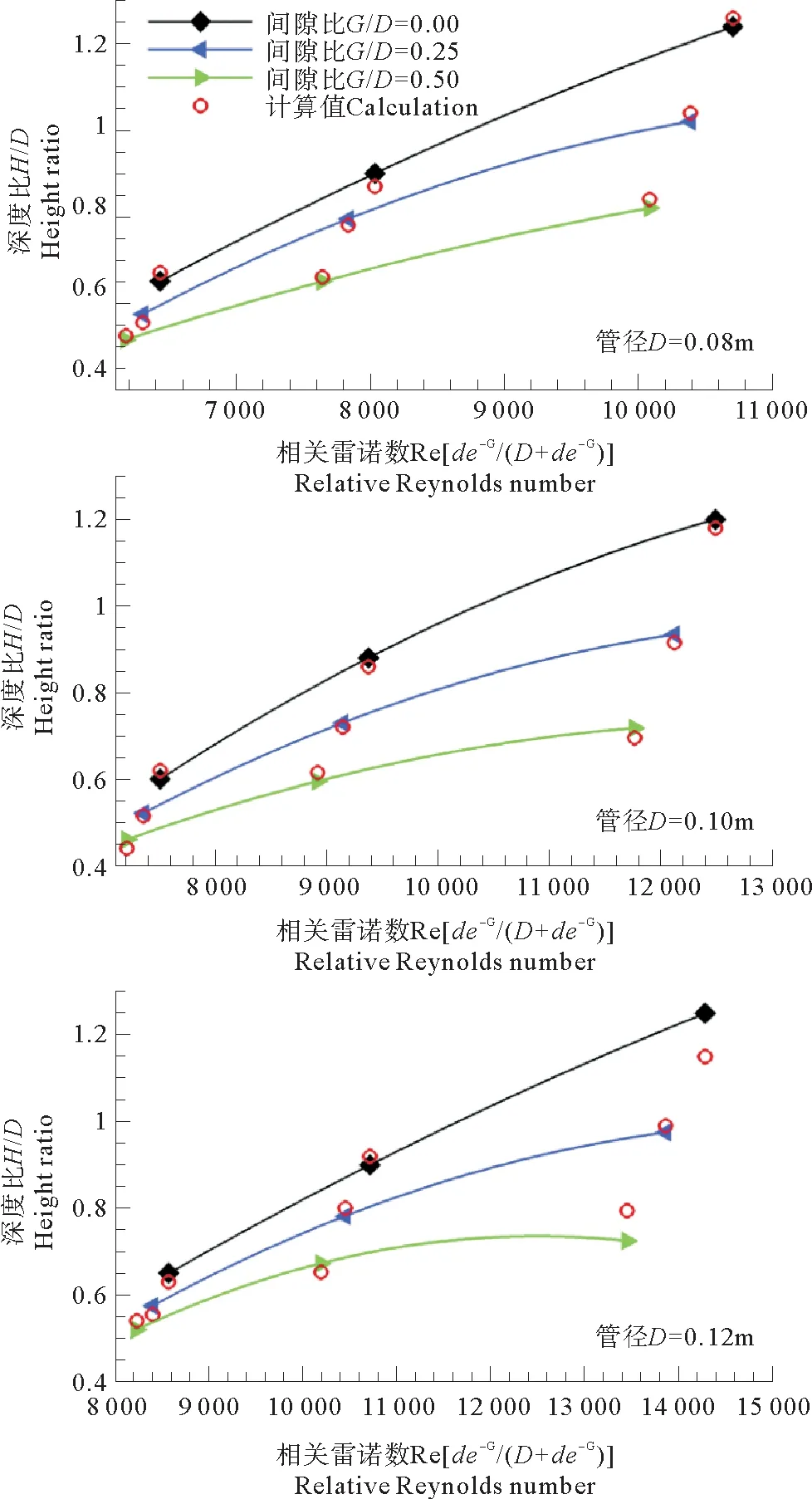
图9 不同条件下冲刷坑计算值与试验值的对比曲线Fig.9 Comparison of calculated values and test data

子母管管径对冲刷坑深度也有很大影响，在相同雷诺数条件下，随着管径的增加，冲刷坑深度与管径之比的比值越小。同时，对比单一结构管线下冲刷坑深度明显增加。Chiew[21]获得的两组试验值也用于验证公式的合理性，结果显示试验值与计算值吻合良好。但也出现了个别点相差较大，笔者认为在试验过程中，流速增加，紊动作用较大出现泥沙冲刷不均匀现象和系统误差造成的。

3 结论

本文研究了子母管不同管径、不同管间间隙、不同流速条件下冲刷坑内泥沙起动、流速分布及冲止流速的情况，在此基础上，讨论了冲刷坑内冲刷深度以及休止角的变化，得出结论如下：

(1)通过试验分析出了不同条件下冲刷坑的变化情况，冲刷坑状态与子母管不同管径，管间间隙及来流流速都有密切的关系，管径越大，间隙越小及来流流速越大，冲刷坑深度越大。

(2)通过不同条件下冲刷对比，得出动水休止角与冲止流速的规律与冲刷坑深度的变化规律相反，随着子母管间间隙及流速的增大而减小。

(3)采用流体的连续性条件，推导了子母管下冲刷稳定时不同试验条件下的冲刷深度计算公式。流速的分布和冲止流速是决定冲刷坑深度的主要因素，该深度与两管间间隙比有直接关系，间隙比越小，冲刷坑深度越大。经试验值与计算值的对比分析，充分验证了该冲刷坑深度计算公式。

不足之处，本文并没有研究子母管与床面存在间隙的情况及该间隙对冲刷坑的影响程度。

[1] Brockbank J. Bundled pipes speed offshore laying[J]. Oil and Gas Journal, 1990, 88(19): 78-84.

[2] 杨玻, 倪浩, 朱晓环. 一种新型的置换海底子母管道技术[J]. 中国造船, 2007, 48: 563-570. Yang H, Ni H, Zhu X H. An Applicable Replacement Bundled Pipeline Structure for Offshore Marginal Oilfield Development[J]. Shipbuilding of China, 2007, 48: 563-570.

[3] 张芝永, 拾兵, 范菲菲, 等. 近床面水平圆柱局部冲刷二维数值模拟[J]. 计算力学学报, 2012, 29(5): 759-764. Zhang Z Y, Shi B, Fan F F, et al. Two-dimensional numerical simulation of local scour around horizontal cylinder near sand bed[J]. Chinese Journal of Computational Mechanics, 2012, 29(5): 759-764.

[4] 刘勇, 拾兵, 杨立鹏, 等. 海底管线作用下的泥沙休止角的试验研究[J]. 海洋湖沼通报, 2012, 4: 31-35. Liu Y, Shi B, Yang L P, et al. Experimental study on the angle of repose of sediment under the action of submarine pipeline[J]. Transactions of Oceanology and Limnology, 2012, 4: 31-35.

[5] Yang L P, Shi B, Guo Y K, et al. Calculation and experiment on scour depth for submarine pipeline with a spoiler[J]. Ocean Engineering, 2012, 55: 191-198.

[6] 夏令. 波浪作用下的泥沙起动及海底管线周围局部冲刷[D]. 浙江: 浙江大学, 2006. Xia L. Study on the Sediment Onset and Local Scour Around Submarine Pipeline Under the Action of Wave[D]. Zhejiang: Zhe Jiang University. 2006.

[7] 潘冬子, 王立忠, 潘存鸿, 等. 推进波作用下海底管线周围局部冲刷实验研究[J]. 海洋工程, 2007, 25(4): 27-35. Pan D Z, Wang L Z, Pan C H, et al. Local scour around pipeline due to progressive wave[J]. The Ocean Engineering, 2007, 25(4): 27-35.

[8] 崔金声, 高福平, 韩希霆, 臧志鹏. 海流作用下子母管结构横向涡激振动[J]. 海洋工程, 2012, 30(1): 18-24. Cui J S, Gao F P, Han X T, et al. Vortex-induced transverse vibration of piggyback pipelines in steady current[J]. The Ocean Engineering, 2012, 30(1): 18-24.

[9] Kalghatgi S G, Sayer P G. Hydrodynamic Forces on Piggyback Pipeline Configurations[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1997, 123: 16-22.

[10] Zhao M, Cheng L. Numerical Modeling of Local Scour below a Piggyback Pipeline in Currents[J]. Journal of Hydraulic Engineering, 2008, 134: 1452-1463.

[11] 马良, 王金英, 孙绍述, 等. 海底(子-母)管道在波流作用下水动力载荷的实验研究[J]. 大连大学学报, 1993, 3(4): 54-63. Ma L, Wang J Y, Sun S S, et al. Experimental Study of Hydrodynamic Force Loading under the Action of Wave Current on Submarine Composite Pipelines[J]. Journal of Dalian University, 1993, 3(4): 54-63.

[12] 成小飞, 王永学, 王国玉. 波流共同作用下海底子母管线水动力的物理模型试验研究[J]. 海洋学报, 2012, 34(4): 172-180. Cheng X F, Wang Y X, Wang G Y. Physical model experimental study of hydrodynamic forces on submarine piggyback pipeline under waver-current coexisting action[J]. Acta Oceanology Sinica, 2012, 34(4): 172-180.

[13] 谷凡, 周晶, 黄承逵, 等. 海底管线局部冲刷机理研究综述[J]. 海洋通报, 2009, 28(5): 110-120. Gu F, Zhou J, Huang C K, et al. Research on mechanism of local scour around submarine pipeline[J]. Marine Science Bulletin, 2009, 28(5): 110-120.

[14] Allen J R L. Simple models for the shape and symmetry of tidal sand waves: statically stable equilibrium forms[J]. Marine Geology, 1982, 48(12): 31-49.

[15] BrØrs B. Numerical modeling of flow and scour at pipeline[J]. Journal of Hydraulic Engineering, 1999, 125(5): 511-523.

[16] 邵学军, 王兴奎. 河流动力学概论[M]. 北京: 清华大学出版社, 2005. Shao X J, Wang X K. Introduction to River Mechanics[M]. Beijing: Tsinghua University Press, 2005.

[17] Cheng L, Chiew Y W. Modeling of flow around a near-bed pipeline with a spoiler[J]. Ocean Engineering, 2003, 30: 1595-1611.

[18] Zhao J, Wang X. CFD Numerical simulation of the submarine pipeline with a spoiler[J]. Journal of offshore mechanics and arctic engineering, 2009, 131(3): 031601-1-031601-5.

[19] 杨兵, 高福平, 吴应湘, 等. 海流引起海底管道悬空的数值模拟[J]. 中国造船, 2005, 46(增刊): 22l-226. Yang B, Gao F P, Wu Y X, et al. Numerical study of the occurrence of pipeline spanning under the influence of steady current[J]. Shipbuilding of China, 2005, 46: 22l-226.

[20] Mao Y. The interaction between a pipeline and an erodible bed[D]. Denmark: The Technology University of Denmark, 1986.

[21] Chiew Y M. Mechanics of local scour around submarine pipelines [J]. Journal of Hydraulic Engineering, 1990, 116(4): 515-529.

Abstract: As an important part of ocean engineering, the submarine pipeline has many advantages when it transports crude oil, such as low coast, safety, quick and convenient. However, with the development of pipeline technology, the normal pipeline can not be satisfied to the various need. Based on the normal pipeline, a new pipeline which is piggyback pipeline is paid more and more attention. As a new type of submarine pipeline, piggyback pipeline has been gradually adopted in engineering practice to enhance the performances and safety of the submarine pipelines. In this paper, according to the present research of normal pipeline, the influence of piggyback pipeline on the local scour is studied based on the experiment and theory analysis. At first, the theory of scour around piggyback pipeline is analyzed. The erosion-stop velocity is deduced firstly. When the scour obtains equilibrium, depending on the force balance, the scour depth calculated formulas around piggyback pipeline are derived due to the erosion-stop velocity and the continuity equation of flow in the pipeline interface. Secondly, the experiment is carried out in an annular flume which can produce the steady flow. Through the experiment, it is found that the main influence factors on the scour are pipeline diameters, gap-ratio and incoming flow velocity. The results show that at a define Reynolds number, the depth of scour hole increases with the decreasing of gap between the main pipe and small pipeline. However, when the gap does not change, the scour depth also increases with the increment of Reynolds number. When the pipe diameter increases, the scour depth under the pipeline is also increase. However, the ratio of scour depth to pipeline diameter decreases slightly. Finally, the calculation values and experimental data are compared. Through the comparison, the calculated values of formulas is well agree with the experimental data and the the accuracy of the formulas is verified. The feasibility of the proposed formula has been well calibrated by both experimental data. The findings drawn from this study are believed to be instructive in the future design and application of the piggyback pipeline.

Key words: piggyback pipeline; scour depth; current; scour mechanism; experiment

责任编辑 陈呈超

Experimental Study on the Local Scour Around the Piggyback Pipeline

PAN Xin-Ying, ZHAO En-Jin, SHI Bing, YU Dong, Huang Xiu-Yun

(College of Engineering, Ocean University of China, Qingdao 266100, China)

P751

A

1672-5174(2017)11-109-08

10.16441/j.cnki.hdxb.20150184

潘新颖， 赵恩金， 拾兵， 等. 海底子母管作用下海床冲刷的试验研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(11): 109-116.

PAN Xin-Ying, ZHAO En-Jin, SHI Bing, et al. Experimental study on the local scour around the piggyback pipeline[J]. Periodical of Ocean University of China, 2017, 47(11): 109-116.

国家自然科学基金项目(51279189)资助 Supported by the National Natural Science Foundation of China (51279189)

2015-04-11；

2016-02-12

潘新颖(1976-)，女，讲师，主要从事海岸及海洋结构动力环境研究。E-mail: xinying@ouc.edu.cn