固定床颗粒层过滤性能分析及预测

颜深，孙国刚，詹敏述，姬忠礼

（1中国石油大学（北京）化学工程学院，北京 102249；2过程流体过滤与分离技术北京市重点实验室，北京 102249；3北京石油化工学院机械工程学院，北京 102617）

固定床颗粒层过滤性能分析及预测

颜深1,2，孙国刚1,2，詹敏述1,3，姬忠礼2

（1中国石油大学（北京）化学工程学院，北京 102249；2过程流体过滤与分离技术北京市重点实验室，北京 102249；3北京石油化工学院机械工程学院，北京 102617）

使用两种滤料颗粒在一套冷态试验装置上考察了过滤气速和颗粒层厚度对颗粒层过滤性能的影响。结合颗粒层过滤宏观模型，分析了不同操作条件下粉尘比沉积率σ对颗粒层粉尘捕集能力偏离初始值程度F和过滤压降偏离初始值程度G的影响，然后预测了过滤效率和压降。结果表明，试验范围内，随着σ的增大，F呈现先增加后降低的变化趋势，而G逐渐增加。结合过滤气速u=0.2～0.6 m·s−1、颗粒层厚度L=0.11～0.2 m条件下的试验数据拟合得到了F-σ和G-σ函数关系，过滤效率和压降的计算值与试验吻合较好，优于文献中相关公式，可为颗粒床过滤性能的预测提供参考。

过滤；固定床；模型；除尘效率；压降

Abstract:The influences of superficial velocity (u) and granular layer thickness (L) on the granular bed filtration performances were investigated in a cold-state experimental apparatus using two kinds of filter media.Combined with the macroscopic model of granular bed filtration,the effects of the specific mass deposit (σ) on the deviation degree (FandG) of dust collecting ability and pressure drop with initial values under different operation conditions were analyzed.On this basis,the prediction of filter efficiency and pressure drop was performed.The results revealed thatFincreased at first and then decreased with increasing ofσ,whileGpresented a linearly increase trend.The functional relationship betweenF(G) andσwas established by combination with experimental data under the condition ofu=0.2～0.6 m·s−1andL=0.11～0.2 m.The calculations of the proposed formulas were in a good agreement with experiments,which were better than the formulas provided in the literature,and thus could provide some guidance for the prediction of performances of granular bed filters.

Key words:filtration; fixed-bed; model; dust removal efficiency; pressure drop

引 言

颗粒床过滤器（简称颗粒床）利用物理和化学性质非常稳定的粒状物料组成颗粒层（也称滤料或过滤介质）实现高温含尘气体除尘，具有兼顾效率与压降、经济性好、苛刻环境适应性强等特点，在固体燃料高效综合利用[1-3]、清洁发电[4]、余热利用[5]等领域应用潜力巨大。颗粒层过滤是一个非稳态过程[6]，粉尘沉积会改变颗粒层空隙结构和滤料颗粒表面特性，过滤效率和压降随之发生变化。因此，研究颗粒层在不同操作条件下的过滤性能变化规律，对颗粒床的科学设计和正常运行具有重要意义。

由于颗粒层微观过滤机理较为复杂，迄今大多数学者通过宏观建模手段[7-17]对颗粒层过滤性能进行预测研究。国内部分学者采用量纲分析方法[13]提出了过滤效率和压降经验公式，虽然与试验值吻合较好，但经验公式没有体现粉尘沉积对颗粒层过滤性能的影响，缺乏普适意义。Tien等[12]总结的“宏观模型”是目前学者们较为普遍接受的预测颗粒层过滤效率和压降的一种方法。该模型采用一组带有未知参数[初始过滤系数λ0、稳态过滤压降(ΔP)0、校正因子F和G等]的微分方程来描述被适当简化的颗粒层过滤过程，这些未知参数与滤料颗粒和含尘气体的特性（直接影响粉尘比沉积率σ）有关，可以通过试验得到。

过滤过程中，伴随着粉尘沉积，颗粒层过滤效率和压降会呈现一种“混合行为”[2,16,18-21]，即效率和压降先随着粉尘沉积而增大，当粉尘沉积至一定程度后，在气流冲刷等作用下，已捕集粉尘会重新返回气流（二次扬尘），效率有所降低，压降趋于稳定。若压降允许，将操作时间适当延长至过滤后期，在效率得到保证的前提下，可降低固定床的反吹频率或移动床的换料频率。当前多数颗粒层过滤宏观模型研究只关注了颗粒层在过滤前期的表现[7,11,14-15]，通过试验得到的F和G是σ的单调递增函数，不能对颗粒层过滤后期的性能变化情况进行预测。目前仅见文献[16]给出一个可以体现颗粒层过滤效率和压降“混合行为”的F-σ和G-σ函数，但它建立在过滤气速低（u=0.15～0.22 m·s−1）、颗粒层厚度小（L=0.05 m）的试验之上，工业应用中颗粒床过滤气速一般维持在 0.3～0.8 m·s−1、颗粒层厚度常取0.1～0.2 m[22]，能否预测高气速、高厚度颗粒层的过滤性能还有待检验。

本研究采用两种滤料颗粒在一套固定床冷态试验装置上考察了颗粒层在工业常用过滤气速和颗粒层厚度条件下长时间运行的性能表现。在试验基础上，结合颗粒层过滤宏观模型，分析了过滤过程中σ对F和G的影响，并由此建立了F-σ和G-σ函数关系，继而对颗粒层过滤效率和压降进行了预测，以期丰富对颗粒层过滤宏观模型的认识。

1 颗粒层过滤宏观模型

1.1 过滤效率预测模型

根据质量守恒定理，假定含尘气体沿颗粒层轴向进行一维均匀流动，并忽略轴向质量扩散的影响，颗粒层过滤宏观控制方程[12]可写成式（1）

初始及边界条件

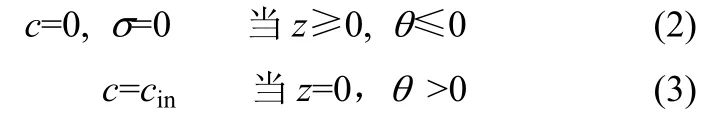
研究发现，含尘气体粉尘浓度沿颗粒层轴向呈对数分布[12]

过滤初期，过滤系数λ基本保持不变，随着粉尘沉积，颗粒层粉尘捕集能力发生变化，λ逐渐偏离其初始值λ0，F表示单位厚度颗粒层过滤能力偏离初始过滤能力的程度[12]

从颗粒层整体质量平衡的角度考虑，并结合式（4），过滤开始后的任一时刻t，颗粒层平均比沉积率σave和平均过滤系数λave计算如下[12,16]

颗粒层瞬时过滤效率E采用式（8）计算

结合式（5）和式（7），式（8）写成

式（9）表明只要明确λ0和F(σave)，便可预测E。

1.2 λ0的确定

如前所述，λ在过滤初期基本保持不变，结合式（4）和式（8），λ0采用式（10）计算

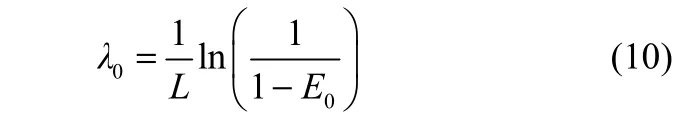
式（10）表明λ0可由过滤初期颗粒层过滤效率E0计算。E0一般可通过试验和经验公式两种方法得到，下面分别予以介绍。

1.2.1 试验计算E0若能在试验中得到t=0时刻颗粒层出口处含尘气体粉尘浓度cout，由式（8）可计算E0，但该值一般较难测量，然而过滤操作中cout随t变化关系是可以通过试验得到的，E0采用式（11）近似计算[12]

1.2.2 经验公式计算E0均匀、随机填充的颗粒物料所构成的颗粒层可认为由N个单元颗粒层（unit bed element，UBE）串联组成。对于圆柱形颗粒层，UBE厚度l采用式（12）计算[12]

过滤初期，认为UBE过滤效率e均相等（e=e0），E0采用式（13）近似计算[12,15-16]

对于圆柱形颗粒层，采用Happel球形模型，e0采用式（14）计算[12]

对于惯性碰撞占主导地位的过滤过程，过滤初期孤立捕集体捕集效率ηs0（single collector efficiency）可由文献[23]中式（19）和式（20）计算。

1.3 过滤压降预测模型

过滤操作中，粉尘沉积除了改变颗粒层过滤能力，还会影响操作压降ΔP，G表示单位厚度颗粒层过滤压降偏离初始过滤压降（稳态过滤压降）的程度[12]

式（15）表明若要预测 ΔP，除G(σave)外，还需明确洁净颗粒层(ΔP)0，这一压降可由Ergun公式[24]计算

2 试 验

2.1 试验装置与测量仪器

冷态试验装置如图1所示，装置主要由颗粒床、气流控制系统、粉尘加料系统及检测系统等组成。固定床颗粒过滤器主体由φ286 mm×1500 mm（外径φ300 mm）有机玻璃筒体构成；筒体下部安装 15 mm×15 mm钢制方形孔网作为滤料支撑结构，孔网上铺设一层250 μm筛网防止滤料漏下。装置内设置3个入风口和2个阀门，通过入风口开闭和阀门切换分别实现正吹过滤和反吹清灰。离心风机负压吸风，螺旋加料器在颗粒层入口处加入粉料形成含尘气流，通过调节加料频率和入口风流量控制cin。u（或入口风流量）由L型皮托管测量；ΔP由U型管压力计测量；cout由德国 Palas公司生产的Promo3000H气溶胶粒径谱仪（时间分辨率1 s）检测，该仪器采样流量固定（5 L·min−1），试验在不更换采样嘴的前提下通过调节旁路补充气体的方式实现等速采样[21,25]。

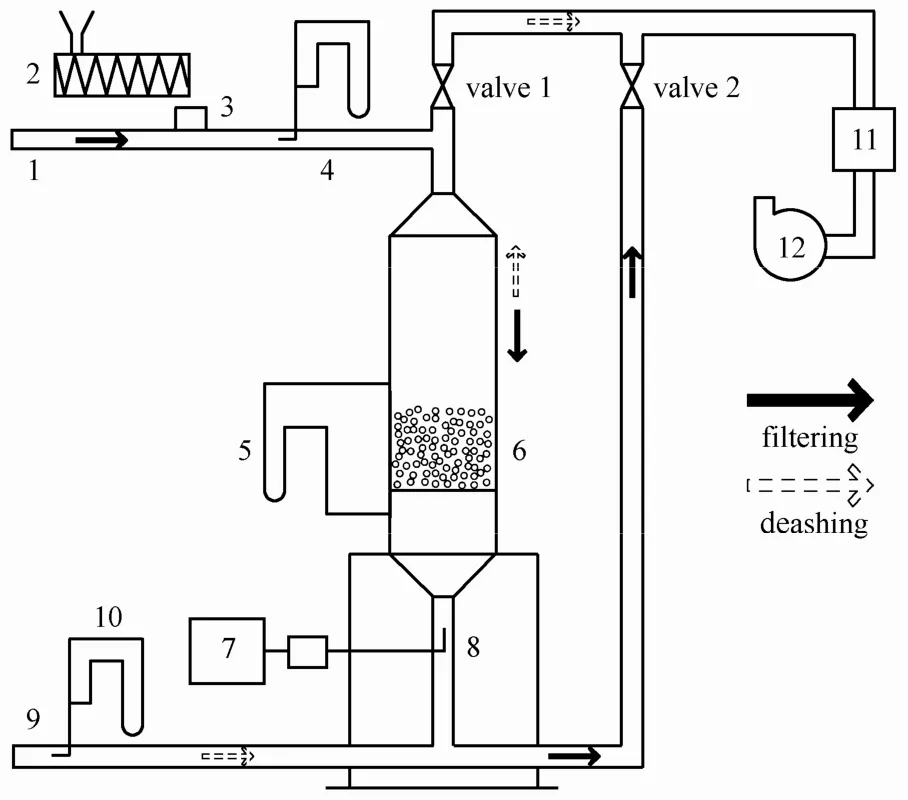
图1 冷态试验装置示意图Fig.1 Schematic diagram of experimental apparatus 1,9—air inlet; 2—screw feeder; 3—feed inlet; 4,10—Pitot tube and U-type pressure gauge; 5—U-type pressure gauge; 6—granular layer; 7—Promo 3000H aerosol spectrometer system; 8—sampling nozzle; 11—bag filter;12—centrifugal fan

2.2 试验物料

试验粉料来自某3000 吨/年固体热载体煤热解中试试验平台产生的粉煤灰，密度约1300 kg·m−3，BT-9300S激光粒度仪测量其体积粒度分布见图2，中位粒径 11.1 μm。试验采用陶瓷球和膨胀珍珠岩作为过滤介质，两种颗粒的基本物性参数见表1。

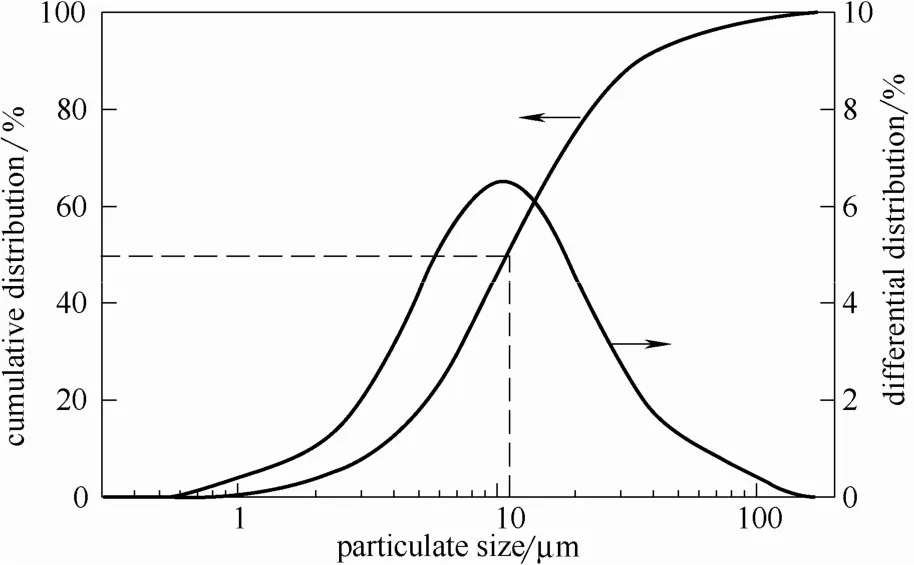
图2 试验粉尘粒度分布Fig.2 Particle size distribution of fly ash

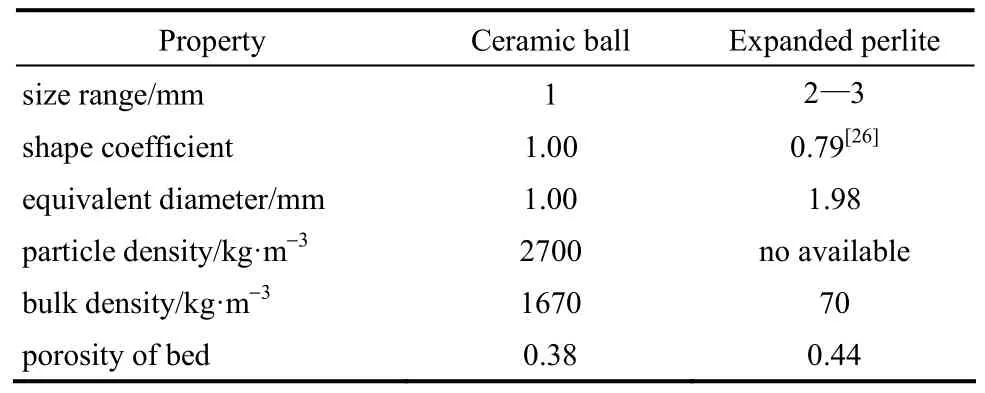
表1 滤料颗粒基本物性参数Table 1 Major properties of filtering media

2.3 试验方法

2.3.1 试验过程与操作条件 在本研究中，首先进行了稳态过滤试验，测量了两种颗粒层在L=0.11、0.2 m，u=0.2～0.8 m·s−1条件下的压降，用以拟合式（16）中可变参数k1、k2和为评价颗粒层反吹清灰质量提供参考。之后进行5组除尘试验，操作条件见表2。

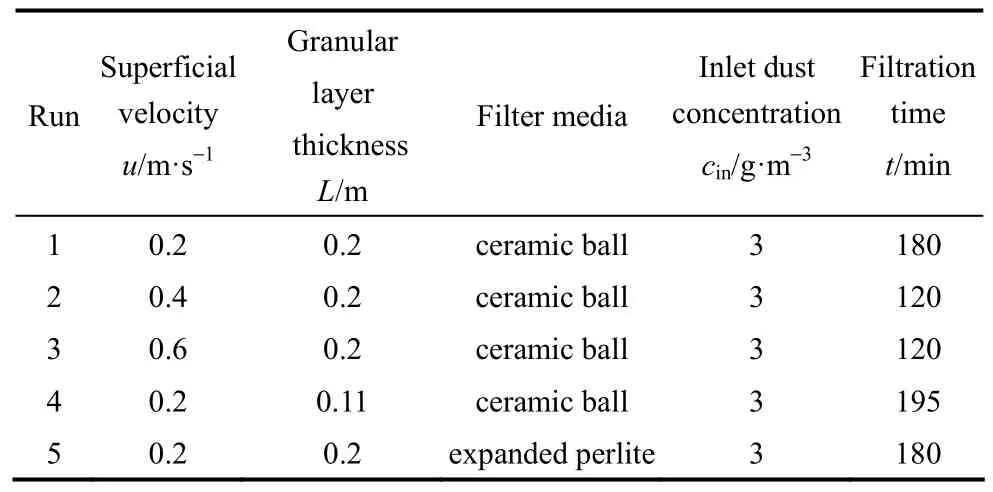
表2 试验操作条件Table 2 Experimental conditions

配尘过滤时，关闭阀1和进气口9，打开进气口1和加料口3，调节阀2开度，由Pitot管4确定u；调节螺旋加料器2加料频率，然后同时启动加料器与Promo3000H气溶胶粒径谱仪，过滤操作自此开始；颗粒层出口处含尘气体经除尘器11进一步过滤后排入大气。试验开始后，间隔5～10 min记录ΔP。随着颗粒层内沉积粉尘的增多，阀2开度逐渐增大，保证u维持在设定值附近。

过滤操作结束后，颗粒层进行反吹清灰，然后进行下次配尘试验。清灰时，关闭阀 2、进气口 1和加料口3，打开气口9和阀1，反吹气体流化颗粒层6，夹带着颗粒层捕集粉尘的气体经除尘器11过滤后排入大气。清灰后颗粒层(ΔP)0与之前稳态过滤试验中测得的(ΔP)0的相对误差不应超过10%（L和u一致情况下），否则应重新进行清灰操作。不同于表面规则且光滑的陶瓷球，膨胀珍珠岩结构非规则且表面粗糙，清灰后仍有相当部分粉尘附着在膨胀珍珠岩表面，为避免这些粉尘对下次过滤试验产生影响，Run 5中不再安排颗粒层清灰，重复试验采用洁净膨胀珍珠岩滤料。

2.3.2 数据分析方法 Promo3000H气溶胶粒径谱仪记录了cout历史数据，试验结束后得到(cout)i-ti变化曲线，其中(cout)i为ti−1～ti期间颗粒层出口处含尘气体粉尘浓度平均值，i初始值1。先由式（10）和式（11）计算λ0，接着由式（5）～式（7）得到F-t和σave-t变化关系，最后拟合得到F(σave) 表达式。本研究也将5次试验的操作条件代入经验公式计算了λ0。

在λ0和F(σave)表达式已知情况下，颗粒层过滤效率预测值Ep可按照以下步骤进行计算：① 假定ti时刻颗粒层平均比沉积率为((σave)p)i；② 将((σave)p)i代入F(σave)表达式得到F(((σave)p)i)；③ 将λ0和F(((σave)p)i)代入式（9）得到(Ep)i；④ 将(Ep)i代入式（6）得到((σave)p)i2；⑤ 若((σave)p)i=((σave)p)i2，则((σave)p)i和(Ep)i分别为ti时刻颗粒层平均比沉积率预测值和过滤效率预测值，此时回到步骤①开始计算ti+1时刻(Ep)i+1；若((σave)p)i≠((σave)p)i2，则回到步骤①重新假定ti时刻((σave)p)i并进行后续计算，直至((σave)p)i=((σave)p)i2。

结合上述Ep计算中得到的(σave)p-t变化关系，颗粒层过滤压降预测值 ΔPp计算步骤如下：① 由ΔP、(ΔP)0及式（15）得到G-t变化关系，结合σave-t变化关系，拟合得到G(σave)表达式；② 将((σave)p)i代入G(σave)表达式得到G(((σave)p)i)；③ 将(ΔP)0和G(((σave)p)i)代入式（15）得到ti时刻(ΔPp)i。

3 结果与讨论

3.1 粉尘沉积对颗粒层过滤压降的影响

陶瓷球和膨胀珍珠岩两种颗粒层(ΔP)0试验值和计算值见图3。在式（16）中，对于陶瓷球，k1=106.79、k2=1.26、R2=0.9972；对于膨胀珍珠岩，k1=170.64、k2=1.45、R2=0.9967。可以看出，Ergun公式很好地预测了试验结果。

图3 (ΔP/L)0试验值和计算值对比Fig.3 Comparison of (ΔP/L)0between experimental and calculated data

图4（a）反映了过滤气速对G值随σave变化情况的影响，可以看出，σave相同时，Run 1的G值明显高于Run 2和Run 3。引起这种差异的主要原因是，气速较低时，粉尘主要沉积于颗粒层上部[27]，这部分颗粒层的内部空隙迅速减小；增大气速，动能随之增加的粉尘可穿过滤料颗粒间的曲折通道深入颗粒层内部，沉积粉尘散布于较大的颗粒层范围内，颗粒层的内部空隙相对较大。由图4（a）也可以看出，Run 2和Run 3的G值相差不大，并以σave=10 kg·m−3为界限分为两个阶段，前后两个阶段G值增加幅度不同。这种现象说明，在较高气速条件下，随着过滤操作的深入进行，沉积粉尘脱落现象越发突出，气流会从某些阻力较小的地方通过，从而产生了固定通道，也就是说颗粒层被穿孔[28]，导致后一阶段G值增加较为平缓。

图4 G试验值和计算值对比Fig.4 Comparison ofGbetween experimental and calculated data

图4（b）反映了颗粒层厚度和滤料种类对G值随σave变化情况的影响。尽管Run 1与Run 5颗粒层空隙率不同，但两者G值却无明显差别。分析原因，Run 5滤料颗粒表面粗糙，比表面积大，粉尘极易黏附于其上[29-30]，在气流吹动下，粉尘也不容易在颗粒层内“滑移”以让出气流通道，沉积粉尘对过流气体较强的阻碍作用导致Run 5压降增幅较大。Run 5的G值在过滤后期逐渐稳定下来，这是因为随着σave的增大，Run 5颗粒层的容尘能力趋于饱和，来流粉尘的沉积量有所减少，气流通道稳定，压降增加不明显。相比之下，在整个过滤过程中，Run 1和Run 4的G值随粉尘沉积呈线性增加变化，说明两者仍有部分颗粒层未被充分利用。过滤结束时，Run 1和Run 4的σave存在较大差异，造成后者压降变化更为显著，其G值约是Run 1的1.5倍。

过滤后期，可以观察到陶瓷球颗粒层顶部形成了较薄的粉尘层。一般来讲，随着过滤操作继续进行，粉尘层逐渐被压实，压降增幅随之增大[27-28]。然而由图4可以看出，试验后期压降并没有出现跃升，这表明粉尘层并没有完全覆盖颗粒层并独自发挥捕集粉尘的作用，过滤操作仍以深层过滤为主导。

Wenzel等[16]基于有关学者研究成果认为G值随σave变化关系可由式（17）表达

将试验数据代入式（17），根据过滤气速、颗粒层厚度及颗粒层空隙率的不同得到了4组G表达式，表达式可变参数、相关系数及适用范围总结于表3。由前述分析可知，σave＞10 kg·m−3时，Run 2和Run 3粉尘二次扬起现象较为突出，颗粒层实际过滤操作时应避免延长过滤时间至这一阶段，将二者拟合范围控制在σave＜10 kg·m−3内。另外，由图4（a）可知，在较高气速条件下，Run 2和Run 3的G值在拟合范围内相差不大，故G表达式由二者统一拟合得到。G试验值与计算值对比见图4，可以看出，式（17）较好地描述了试验G值随σave变化情况。

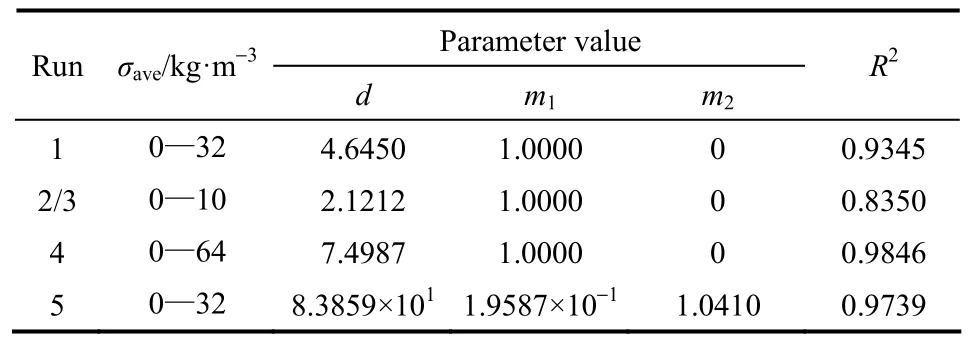
表3 G表达式相关参数Table 3 Parameter values ofGexpression

3.2 粉尘沉积对颗粒层粉尘捕集能力的影响

试验法和经验公式法得到的λ0总结于表4。λ0表征单位厚度颗粒层的初始过滤能力，Run 1和Run 4经验公式计算表明，在其他操作条件相同时，λ0与颗粒层厚度无关；而试验结果更加贴近实际，即在一定范围内，颗粒层厚度的增大对过滤是有利的，厚度继续增大，粉尘捕集能力增加不明显，这解释了为什么颗粒层厚度相对较小的Run 4的λ0会大于Run 1。Run 1～3经验公式计算的λ0随气速的增大而减小，这与经验公式的适用条件相吻合，而试验表明颗粒层厚度增至一定程度后，气速的变化对颗粒层初始过滤能力无显著影响。由Run 1和Run 5可知，颗粒层的初始过滤能力也受空隙率影响，空隙率较小的颗粒层的λ0相对较大。需要注意的是，在Run 1～5中，两种方法得到的λ0均存在一定程度的偏差，这表明在经验公式法中，过滤初期e均相等这一假设应用于颗粒层较厚的场合存在一定的局限性。所以，试验法得到的λ0被应用于后续计算。

表4 试验和经验公式计算λ0对比Table 4 Comparison ofλ0obtained by experiment and empiric equation/m−1

图5给出了颗粒床出口粉尘浓度随时间变化情况（以Run 4为例），用以后续计算。

图5 出口粉尘浓度随时间变化情况Fig.5 Relationship between outlet dust concentration and time

图6反映了不同操作条件下粉尘沉积对颗粒层过滤能力偏离初始值程度的影响，可以看出，5次试验F值随σave的增大均呈现先增加后降低的变化趋势，这从粉尘沉积的角度解释了过滤过程中颗粒层过滤效率呈现“混合行为”的原因。

如前所述，在其他操作条件相同时，气速偏低，粉尘会在颗粒层上部“集中”分布，气速偏高，粉尘则倾向于在颗粒层内“均匀”分布，这解释了图6（a）中σave相同时，颗粒层在低气速下的过滤表现要优于高气速这一情况的发生。对于Run 2和Run 3，σave＞2.5 kg·m−3时，二次扬尘现象逐渐显现，颗粒层沉积粉尘重新返回气流，F值迅速降低，从峰值降至1，Run 2用时约20 min，Run 3用时约12 min。而对于Run 1，因沉积粉尘主要分布于颗粒层上部，重新返回气流的粉尘可能在颗粒层下部被重新捕集，F值则缓慢降低，从峰值降至1用时约140 min。

图6（b）反映了颗粒层厚度和滤料种类对F值随σave变化情况的影响。相较于Run 4，Run 1颗粒层厚度大，难以穿透，更多的粉尘被捕集并沉积下来，颗粒层过滤能力较初始值明显增强，图中表现为其F峰值是Run 4的1.2倍左右。一般来说，对于同一种滤料颗粒，在其他操作条件相同时，颗粒层厚度越大，其容尘量也越大，但是单位厚度颗粒层的容尘能力却不会有明显差别，然而由图6（b）可以看出，过滤操作结束时，颗粒层厚度相对较小的Run 4的σave却近乎是Run 1的2倍，这种差异产生的原因是，Run 1颗粒层较厚，在有限的操作时间内，粉尘主要沉积于颗粒层上部，下部颗粒层未能充分发挥捕集粉尘的作用，而用来计算σave的式（6）中的L却是颗粒层的总体厚度，这无疑降低了σave的数值。将滤料颗粒更换为膨胀珍珠岩，因颗粒层空隙率较大，粉尘沉积对颗粒层过滤能力的增强作用相对不明显，其F峰值低于Run 1。

将试验数据代入与式（17）形式相似的式（18）[16]进行拟合，同样得到了4组F表达式，其可变参数、相关系数及适用范围见表5，F试验值与计算值对比见图6。其中，Run 2和Run 3的F值在σave＞10 kg·m−3时降至 1 以下，表明此时颗粒层过滤能力已低于初始值，故F表达式拟合范围与G表达式保持一致，控制在σave＜10 kg·m−3范围内。另外，由图6（a）可知，在较高气速条件下，颗粒层粉尘捕集能力对气速变化并不敏感，F表达式由二者统一拟合得到。

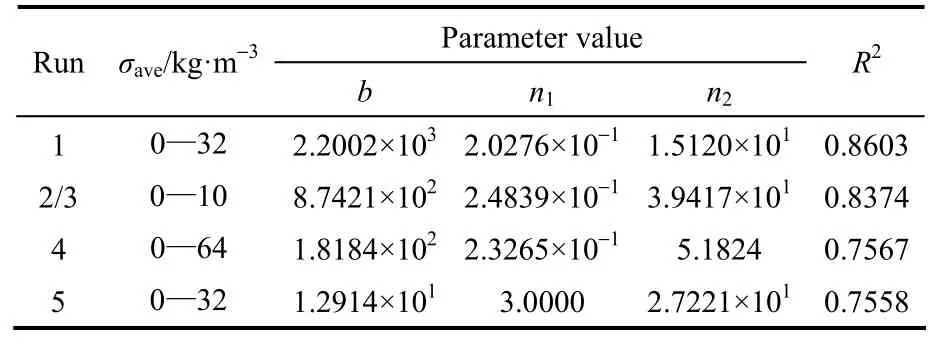
表5 F表达式相关参数Table 5 Parameter values ofFexpression

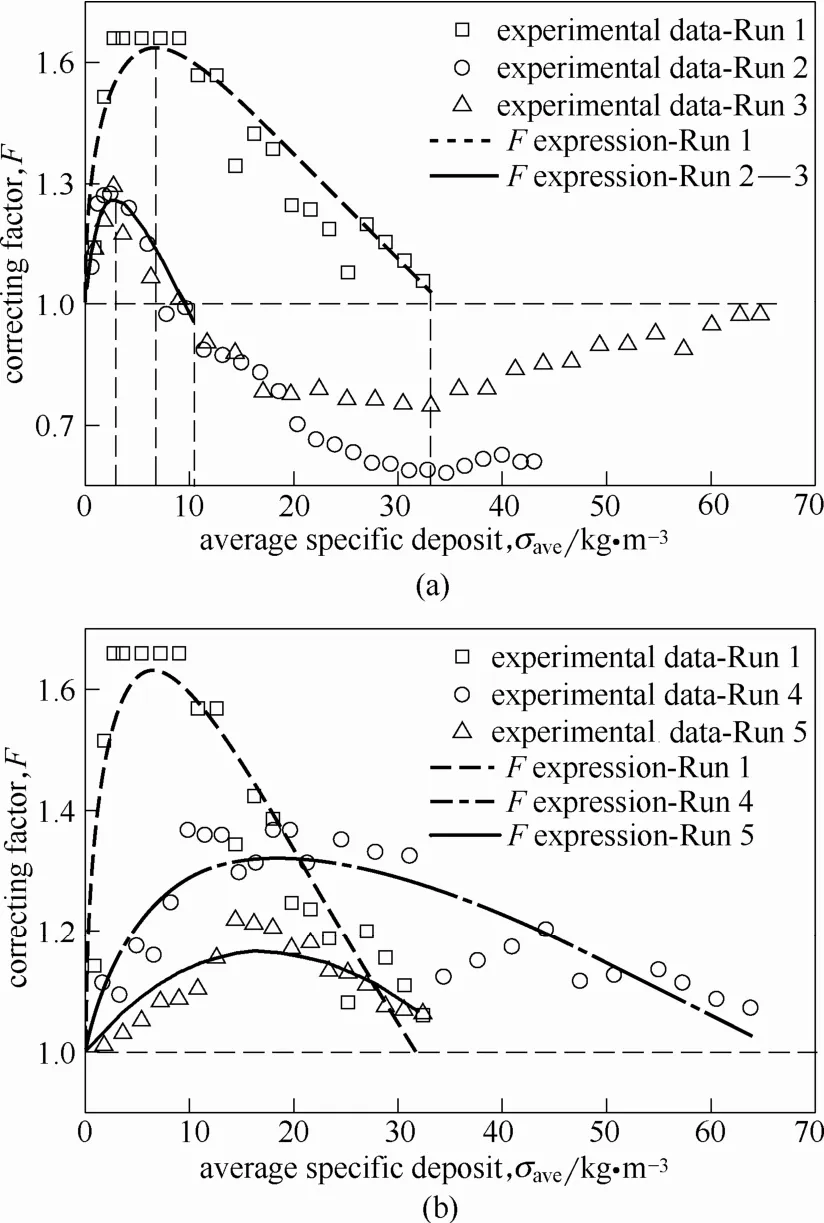
图6 F试验值和计算值对比Fig.6 Comparison ofFbetween experimental and calculated data

3.3 过滤效率和压降预测

利用2.3.2节给出的数据分析方法得到的ti时刻σave预测值与试验值对比见图7，可以看出两者基本一致。

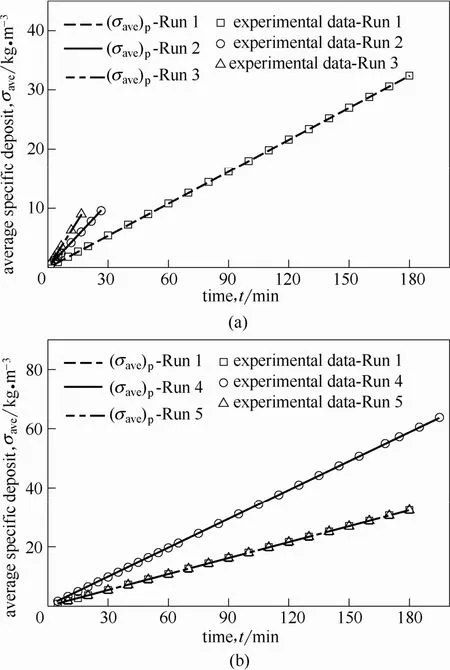
图7 σave试验值和预测值对比Fig.7 Comparison ofσavebetween experimental and predicted data

图8给出了5组试验颗粒层过滤性能随过滤时间变化曲线，由图可知，增大陶瓷球颗粒层厚度至一定程度后，气速的改变对E无明显影响，虽然高气速下颗粒层的处理气量得以增大，但ΔP也随之上升。相比之下，膨胀珍珠岩在过滤过程中表现出了高效率低压降的特点，但是这种滤料表面多孔、强度低、再生质量差，不适合长时间循环使用。

以(σave)p-t变化关系为基础，结合试验数据拟合的F和G表达式，得到的E和ΔP预测值见图8。作为对比，图8还给出了利用文献[16]中F和G表达式（适用范围σave=0～195 kg·m−3）计算的E和 ΔP值，以验证依低气速、小厚度颗粒层试验建立的宏观模型预测本研究操作条件下的颗粒层过滤性能的可行性。可以看出，文献[16]模型预测值仅与较低气速条件下的Run 1、Run 4和Run 5操作前期的试验值较吻合，随着过滤时间的增加，预测值与试验值偏差较大。相比之下，在拟合范围内，本研究计算得到的Ep较好地预测了试验E随过滤时间增加表现出的先升高后降低的变化规律，与此同时，ΔPp也与过滤过程中逐渐增加的ΔP吻合较好。

4 结 论

（1）试验范围内，随着粉尘比沉积率σ的增大，颗粒层粉尘捕集能力偏离初始值程度F呈现出先增加后降低的变化趋势，而过滤压降偏离初始值程度G逐渐增加。这从粉尘沉积的角度解释了过滤操作中颗粒层效率和压降表现出“混合行为”的原因。

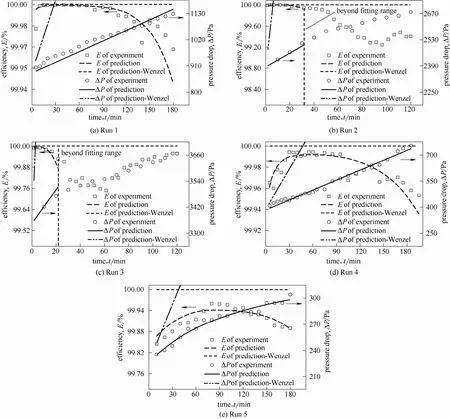
图8 E和ΔP试验值和预测值对比Fig.8 Comparison ofEand ΔPbetween experimental and predicted data

（2）不同操作条件下，颗粒层F和G值随σ的变化程度是有差异的。从颗粒层充分利用角度考虑，低过滤气速应与小颗粒层厚度相配合。在压降允许情况下，采用较大颗粒层厚度，增大处理气量的同时，过滤效果也可得以满足。优先选用表面粗糙、结构非规则的滤料颗粒，但其强度也应得到保证。

（3）依据过滤气速u=0.2～0.6 m·s−1、颗粒层厚度L=0.11～0.2 m条件下的试验数据，拟合获得了F-σ和G-σ函数关系，结合颗粒层过滤宏观模型计算的效率和压降预测值与试验值吻合较好，优于文献[16]中相关公式，可为颗粒床过滤性能的预测提供参考。后续应继续开展不同操作条件下F-σ和G-σ函数关系试验研究，寻找共性，以丰富颗粒层过滤宏观模型。

符 号 说 明

b,d,k1,k2,m1,m2,n1,n2——可变参数

c——含尘气体粉尘浓度，kg·m−3

dg——滤料颗粒直径，m

E——颗粒层过滤效率，%

e——单元颗粒层过滤效率，%

F,G——校正因子

L——颗粒层厚度，m

l——单元颗粒层厚度，m

N——单元颗粒层数量（整数）

ΔP——颗粒层过滤压降，Pa·m−1

R2——相关系数

t——过滤时间，s

u——表观过滤气速，m·s−1

z——颗粒层轴向方向，m

ε0——洁净颗粒层空隙率

ηs——孤立捕集体捕集效率，%

θ——校正时间（通常θ与t差别很小，取θ≈t），s

λ,λave——分别为过滤系数和平均过滤系数，m−1

μf——气体动力黏度，Pa·s

ρf——气体密度，kg·m−3

σ,σave——分别为比沉积率、平均比沉积率，kg·m−3

下角标

in,out ——颗粒层入口处、出口处

i——时间点

p ——预测值

0 ——过滤初期阶段

[1]战金辉,赖登国,许光文.油页岩: 固体石油[J].科学世界,2016,(12): 68-73.ZHAN J H,LAI D G,XU G W.Oil shale: solid petroleum[J].Science World,2016,(12): 68-73.

[2]詹敏述.油页岩与固体热载体颗粒混合及热解气高温除尘技术研究[D].北京: 中国石油大学(北京),2015.ZHAN M S.Research on the mixing of oil shale and solid heat carriers and high temperature pyrolysis gas dust removal technology[D].Beijing: China University of Petroleum,2015.

[3]能源转化课题组.中国科学院过程工程研究所煤炭低温热解油尘分离技术获得突破性进展[EB/OL].[2017-04-05].http://www.ipe.cas.cn/xwdt/kyjz/201504/t20150410_4334971.html.Energy conversion research group.Institute of Process Engineering,Chinese Academy of Sciences made a great breakthrough in the separation technology of oil and dust in the process of low-temperature pyrolysis of coal [EB/OL].[2017-04-05].http://www.ipe.cas.cn/xwdt/kyjz/201504/t20150410_4334971.html.

[4]SMID J,PENG C Y,LEE H T,et al.Hot gas granular moving bed filters for advanced power systems[J].Filtration and Separation,2004,41(10): 32-35.

[5]于春令,杨国华,王兴云.双层滤料颗粒床高温除尘技术及其在冶金炉窑中的应用[J].环境工程,2009,27(2): 15-17,21.YU C L,YANG G H,WANG X Y.Dual-layer granular bed filter for hot gas cleanup and its application in metallurgical furnaces[J].Environmental Engineering,2009,27(2): 15-17,21.

[6]ZAMANI A,MAINI B.Flow of dispersed particles through porous media—deep bed filtration[J].Journal of Petroleum Science and Engineering,2009,69(1/2): 71-88.

[7]WALATA S A,TAKAHASHI T,TIEN C.Effect of particle deposition on granular aerosol filtration: a comparative study of methods in evaluating and interpreting experimental data[J].Aerosol Science and Technology,1986,5(1): 23-37.

[8]BAI R,TIEN C.Effect of deposition in deep-bed filtration:determination and search of rate parameters[J].Journal of Colloid and Interface Science,2000,231(2): 299-311.

[9]吴晋沪,王洋.移动床除尘过程数学模型建立及机理讨论[J].燃料化学学报,2002,30(3): 218-222.WU J H,WANG Y.Establishment of mathematical model of moving granular bed for dust removal process and discussion of process mechanism[J].Journal of Fuel Chemistry and Technology,2002,30(3): 218-222.

[10]赵建涛,黄戒介,吴晋沪,等.气固错流移动颗粒床过滤器除尘效率[J].化工学报,2004,55(5): 721-726.ZHAO J T,HUANG J J,WU J H,et al.Collection efficiency of cross-flow moving granular bed filter[J].Journal of Chemical Industry and Engineering(China),2004,55(5): 721-726.

[11]MACIAS-MACHIN A,SOCORRO M,VERONA J M,et al.New granular material for hot gas filtration: use of the “Lapilli”[J].Chemical Engineering and Processing,2006,45(9): 719-727.

[12]TIEN C,RAMARAO B V.Granular Filtration of Aerosols and Hydrosols[M].2nd ed.Oxford: Elsevier Science,2007: 21-116.

[13]付海明,李阳.颗粒层过滤器过滤性能优化模型[J].环境工程,2009,27(S1): 250-254.FU H M,LI Y.Optimized model of performance of granular bed filter[J].Environmental Engineering,2009,27(S1): 250-254.

[14]颜学升,张敏,王助良,等.新型颗粒层过滤性能的宏观数学模型[J].环境工程学报,2009,3(12): 2285-2290.YAN X S,ZHANG M,WANG Z L,et al.Macroscopic mathematical model for predicting filtration performance of a new granular layer[J].Chinese Journal of Environmental Engineering,2009,3(12):2285-2290.

[15]SULAYMON A H,MUSTAFA Y A.Aerosol filtration using quartz sand filter[J].American Journal of Environmental Science,2012,8(4):385-395.

[16]WENZEL B M,PORCIUNCULA C B,MARCILIO N R,et al.Filtration of dust in an intermittent moving granular bed filter:performance and modeling[J].Separation and Purification Technology,2014,133(36): 108-119.

[17]刘书贤,黄峰,苌亮,等.颗粒过滤器除尘效率的实验研究与数学建模[J].煤炭学报,2016,41(S2): 542-547.LIU S X,HUANG F,CHANG L,et al.Mathematical modeling and experimental study on dust removal efficiency of granular filtration bed[J].Journal of China Coal Society,2016,41(S2): 542-547.

[18]谭天佑,梁凤珍.工业通风除尘技术[M].北京: 中国建筑工业出版社,1984: 179-181.TAN T Y,LIANG F Z.Industrial Ventilation and Dust Removal Technology[M].Beijing: China Architecture and Building Press,1984:179-181.

[19]许世森.移动颗粒层过滤高温除尘过程结构和参数优化实验研究[J].中国电机工程学报,1999,19(5): 13-17.XU S S.Research on optimizing structure and parameters of the moving granular bed filter for high temperature dust removal in IGCCand PFBC systems[J].Proceedings of the Chinese Society for Electrical Engineering,1999,19(5): 13-17.

[20]李翔,白皓,苍大强,等.固体颗粒床高温除尘器的等温实验研究[J].北京科技大学学报,2004,26(1): 18-21.LI X,BAI H,CANG D Q,et al.Isothermal experiment research of a high temperature granular bed filter[J].Journal of University of Science and Technology Beijing,2004,26(1): 18-21.

[21]TIAN S R,YANG G H,LI Z,et al.Cascade fi ltration properties of a dual-layer granular bed fi lter[J].Powder Technology,2016,301:545-556.

[22]向晓东.现代除尘理论与技术[M].北京: 冶金工业出版社,2002:159-160.XIANG X D.Modern Aerosol Particle Collection Theory and Technology[M].Beijing: Metallurgical Industry Press,2002: 159-160.

[23]JUNG Y,WALATA S A,TIEN C.Experimental determination of the initial collection efficiency of granular beds in the inertial-impaction-dominated region[J].Aerosol Science and Technology,1989,11(2): 168-182.

[24]ERGUN S.Fluid flow through packed columns[J].Chemical Engineering Progress,1952,48(2): 89-94.

[25]黄三.自带粉体层滤膜的多层滤料颗粒床过滤特性研究[D].宁波:宁波大学,2012.HUANG S.Study on characteristics of the multi-layer granular bed with powder membrane[D].Ningbo: Ningbo University,2012.

[26]吴占松,马润田,汪展文.流态化技术基础及应用[M].北京: 化学工业出版社,2006: 51-52.WU Z S,MA R T,WANG Z W.Fluidization Technology Foundation and Application [M].Beijing: Chemical Industry Press,2006: 51-52.

[27]岑可法,倪明江,严建华,等.气固分离理论及技术[M].杭州: 浙江大学出版社,1999: 494,499.CEN K F,NI M J,YAN J H,et al.Gas-Solid Separation Theory and Technology[M].Hangzhou: Zhejiang University Press,1999: 494,499.

[28]KUO Y M,HUANG S H,LIN W Y,et al.Filtration and loading characteristics of granular bed fi lters[J].Journal of Aerosol Science,2010,41(2): 223-229.

[29]白皓,齐道辉,钱文涛,等.微米级气溶胶粒子在滤层中的收集效率研究[J].过程工程学报,2009,9(S1): 31-35.BAI H,QI D H,QIAN W T,et al.Study on filtrating efficiency of micron aerosol particles by granular bed filter[J].The Chinese Journal of Process Engineering,2009,9(S1): 31-35.

[30]SHI K Y,YANG G H,HUANG S,et al.Study on fi ltering characteristics of aerosol particulates in a powder-grain dual-layer granular bed[J].Powder Technology,2015,272: 54-63.

Analysis and prediction of fixed granular bed filtration performances

YAN Shen1,2,SUN Guogang1,2,ZHAN Minshu1,3,JI Zhongli2
(1College of Chemical Engineering,China University of Petroleum,Beijing102249,China;2Beijing Key Laboratory of Process Fluid Filtration and Separation,Beijing102249,China;
3College of Mechanical Engineering,Beijing Institute of Petrochemical Technology,Beijing102617,China)

TQ 028.2；TQ 051.8

A

0438—1157（2017）10—3841—10

10.11949/j.issn.0438-1157.20170379

2017-04-10收到初稿，2017-07-01收到修改稿。

联系人：孙国刚。

颜深（1994—），男，硕士研究生。

国家重点基础研究发展计划项目（2014CB744304）；中国科学院过程工程研究所多相复杂系统国家重点实验室开放课题（MPCS2014D11）。

Received date:2017-04-10.

Corresponding author:Prof.SUN Guogang,ggsunbj@163.com

Foundation item:supported by the National Basic Research Program of China (2014CB744304) and the Open Project Program of Institute of Process Engineering,Chinese Academy of Sciences (MPCS2014D11).