基于AIS的对海雷达多目标联合误差估计方法*

2017-10-16姜佰辰王国庆

火力与指挥控制 2017年9期

关键词：航迹关联雷达

姜佰辰，孙璐，周伟，王国庆，关键

（海军航空大学，山东烟台 264001）

基于AIS的对海雷达多目标联合误差估计方法*

姜佰辰，孙璐，周伟，王国庆，关键

（海军航空大学，山东烟台 264001）

提出了一种基于AIS的对海警戒雷达多目标联合误差估计方法，该方法以高精度AIS提供的目标信息为目标真值，对雷达进行误差估计。利用系统积累的多目标航迹信息，首先进行目标粗关联，将航迹信息进行时空对准后产生误差序列，通过单目标误差序列统计信息进行异常值的筛选，再通过多目标误差序列进行错误关联目标的检验，最终对剩余误差序列进行误差估计。通过实测数据和实际应用证明，该方法估计的雷达误差较准确，用估计结果对雷达误差进行校准后可有效减小对海雷达的系统误差。

自动识别系统，对海雷达，误差估计

Abstract：A multi-target joint bias estimation method for sea surveillance radar based on AIS is proposed in this paper.Using the AIS with the higher precision as target true value，by which estimates the bias of radar.Based on the multi-target track data，firstly associates the tracks in the presence of systematic bias，then generates the error series after temporal and space alignment.With one target error series，filtrates the abnormal track point，then eliminate the false correlated track by statistical test using multi-target error series.At last，the system bias is estimated.The measured data and practical application shows that this method can properly estimate the bias，and the system bias is effectively reduced after calibration with the estimated result.

Key words：automatic identification system，sea surveillance radar，bias estimation

0 引言

近年来，掌控海上综合态势已越来越重要，各类态势信息的融合处理，对系统中各类传感器的指标要求越来越高［1］。对海雷达的系统误差会随着工作时间的延长而积累，近年的研究表明［2-3］，雷达系统误差会降低与其他传感器航迹正确关联的概率，进而影响后续的融合处理，且误差增大会增加融合的难度，因此，需要定期对雷达系统误差进行校准。

传统的误差校准方法主要是以配备高精度差分GPS设备的舰船为配合目标进行标校［4］，该方法需要专门的目标船进行配合，受限于成本，一般只会派出一艘舰船，导致目标单一，且活动范围有限，不能覆盖雷达主要探测区域，易产生较片面的误差校准结果。

随着船舶自动识别系统（Automatic Identification System，AIS）的广泛应用，海上主要船舶均配备了AIS，AIS可以提供GPS等高精度的船舶定位信息。近年基于AIS信息进行雷达误差标校逐渐成为主流［5-8］。文献［5］是选取某个合适的目标进行误差标校，目标单一且主观性较大，不能涵盖各类运动状态的目标。利用多目标进行标校比较普遍［6-8］，但目前的研究成果仍处于研究阶段，主要在仿真环境下对方案可行性进行了研究，设置了较多的假设条件，如目标运动较为理想、目标分布较散等，这些与实际应用环境有较大出入，且未考虑雷达工作性能等因素。

通过对大量实测数据进行分析，发现雷达覆盖区域中的多目标误差样本相对较为集中，在统计上趋于正态分布，一般情况下仅含有少量较大随机误差的测量值，少数情况下会有一些错误测量值。众多雷达误差分析方面的研究成果，都将雷达的测量随机误差建模为高斯白噪声［3，9］，这部分对后续误差分析中的影响较小，可以忽略［10］。在集中区域之外出现的测量样本，主要是因为目标密集、目标航迹交汇、雷达跟踪性能不稳定等原因导致目标漏跟、错跟带来的错误目标测量值；还有一些错误测量值，是由于错误的航迹关联导致测量值与真值的错误配对，从而带来一部分错误测量结果。这些错误测量值是不能将其纳入误差估计样本中的，且这类错误测量的存在往往会严重影响误差估计结果。

应用于真实环境中的实测数据，必须对上述几种错误测量值进行筛选和剔除，再进行多目标联合误差估计，才能保证最终结果的可靠。实际应用证明，本文方法在对海雷达系统测量误差标校中取得了较为理想的效果。

1 问题描述

设传感器A为对海雷达，传感器B为AIS，传感器A和传感器B可以同时探测到M个目标。

传感器A有2个属性测量值，分别为距离ρ和方位θ，其对目标的测量向量为，且测量属性之间相互独立。设为传感器A对i目标在k时刻的测量向量，其中；由于传感器B与传感器A是异类传感器，其对目标的测量向量是不同的，需通过空间坐标变换得到与传感器A同维且同属性的测量向量，设为传感器B对i目标在k时刻的测量向量；传感器B测量结果转换得到的，即视为传感器A的测量参考真值。由于雷达距离测量和方位测量相互独立，对二者误差序列的分析方法相同，不失一般性，本文以距离误差序列分析为例对误差估计过程进行介绍。

设ni为传感器A对i目标在数据采集时间内获得的目标测量样本数，那么为传感器A探测到的M个目标测量样本数的总和。

本文后续介绍的异常航迹点筛选方法和错误关联目标剔除方法，将主要基于上述统计量进行。

另外，在对海雷达误差校准的实际应用过程中，还应遵循以下几条原则。

（1）雷达测量值均为原始测量值，不进行任何形式的变换，以减少转换过程中带来的误差积累；

（2）雷达和AIS系统使用统一的授时设备进行授时，确保系统时间一致。

2 雷达误差估计方法

本文提出的对海雷达误差估计方法主要包含以下几个步骤：

（1）系统误差条件下的航迹粗关联；

（2）雷达航迹时间对齐；

（3）单目标误差序列异常值筛选；

（4）错误关联目标剔除；

（5）估计传感器系统误差。如下页图1所示为对海雷达误差估计完整流程图。

2.1 航迹粗关联

图1 误差估计流程图

设 AIS的目标集合为 TB，对坌b∈TB，有，其中idb表示 AIS的目标批号，ρb和θb分别为经空间坐标变换后AIS的距离和方位测量值。空间坐标变换已有较多研究成果，本文参考了文献［11］的坐标转换方法。设Δρ和Δθ分别为对海雷达的距离精度和方位精度，则以为距离筛选区间，以为方位筛选区间对雷达的目标进行筛选，同时满足距离和方位筛选区间的雷达目标加入雷达目标集合TA，对，有，其中ida表示雷达的目标批号，ρa和θa分别为雷达的距离和方位测量值，再以为距离筛选区间，以为方位筛选区间对AIS目标进行反馈筛选，同时满足两个筛选区间的AIS目标加入a的配对目标集合Ca，若对，其配对目标集合Ca有且只有一个元素，则完成目标配对；否则，以Δρ和Δθ为步进长度，减小距离和方位筛选区间继续进行筛选，直到配对目标集合Ca中有且只有一个元素，则完成雷达与AIS目标的粗关联；若某次筛选时集合Ca为空，则将a从TA中剔除。

2.2 时间对齐

虽然雷达与AIS有统一的授时设备，并不代表二者产生的测量结果时刻是一致的。例如雷达有扫描周期，每一圈或几圈产生一个测量结果，而AIS的船位报告时间间隔有其规范［12］，各自产生的目标航迹时刻一般不相同，因此，需要对航迹数据进行时间对齐。

其中ρb'和θb'分别为插值得到的AIS在t时刻的距离和方位测量值。

2.3 单目标误差序列异常值筛选

步骤2 若存在筛选区间外的样本，剔除筛选区间外的样本，重新计算剩余所有样本的均值和方差，返回步骤1继续进行；

步骤3 若序列中所有样本都包含于筛选区间内，则完成目标距离误差序列的异常值筛选。

需要说明的是，剔除距离误差样本的同时，其对应的方位误差样本将同时被剔除，对方位误差序列进行异常值筛选时也是如此。

2.4 错误关联目标剔除

步骤2 除i目标距离误差序列以外的剩余所有目标距离误差序列的集合，记为，计算R的均值、标准差，计算公式如下：

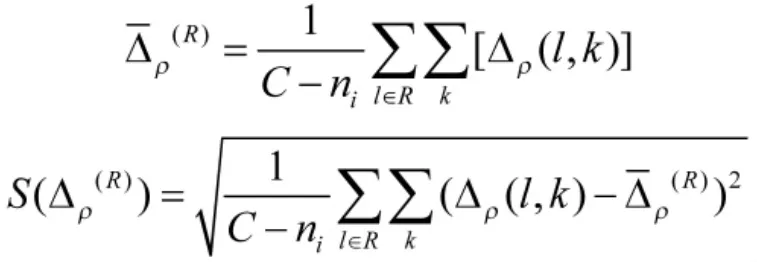
步骤3 在显著性水平为α的条件下对假设

进行检验，取检验统计量为

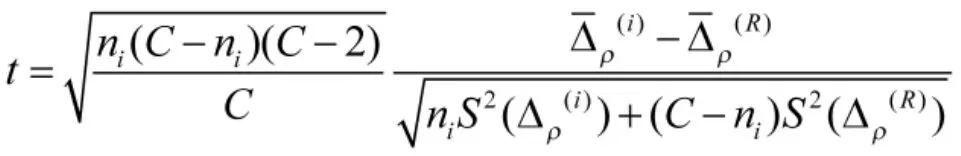
则t服从自由度为C-2的t分布，否定域为

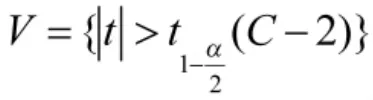
若i目标不满足否定域的条件，即不能否定H0，则判定i目标为正确关联，予以保留，反之，则将判定i目标为错误关联，将其误差序列予以剔除，更新M、C和，返回步骤1继续进行；

步骤4 若所有目标均满足假设条件，则完成距离误差序列的错误关联剔除。

与前一过程类似，若某个目标距离误差序列不满足假设予以剔除时，该目标的方位误差序列也会同时被剔除，对方位误差序列进行检验时也是如此。

2.5 传感器误差估计

设完成异常航迹筛选和错误关联提出的所有目标距离误差序列为，则将的均值作为距离误差估计结果：

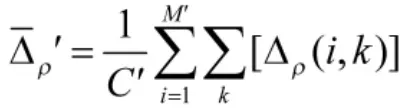
其中，M'表示剩余误差序列的关联目标总数，C'表示剩余误差序列的误差点数。

3 实验结果与分析

实验分为误差标定实验和验证实验，误差标定实验过程采集的数据为计算传感器误差所用，完成误差标定后，对传感器系统进行误差校准，再使用同样的方法进行验证实验。两次实验的数据均使用某站实地采集的目标航迹数据，雷达目标为半自动录取，即人工起始，自动跟踪。

误差标定实验的数据采集时间共83 min，共采集到该型雷达上报的目标航迹70批，AIS目标1 738批，其中实现粗关联的目标共54对（仅使用船位精确度为高的目标数据），经空间坐标变换和航迹的时间对齐后，误差序列共4 934个样本。以距离误差估计为例对误差标定实验过程进行介绍。

所有粗关联目标距离误差序列统计直方图如图2所示，在统计区间外还有大量的样本，主要是错误关联目标和目标异常值所导致的。

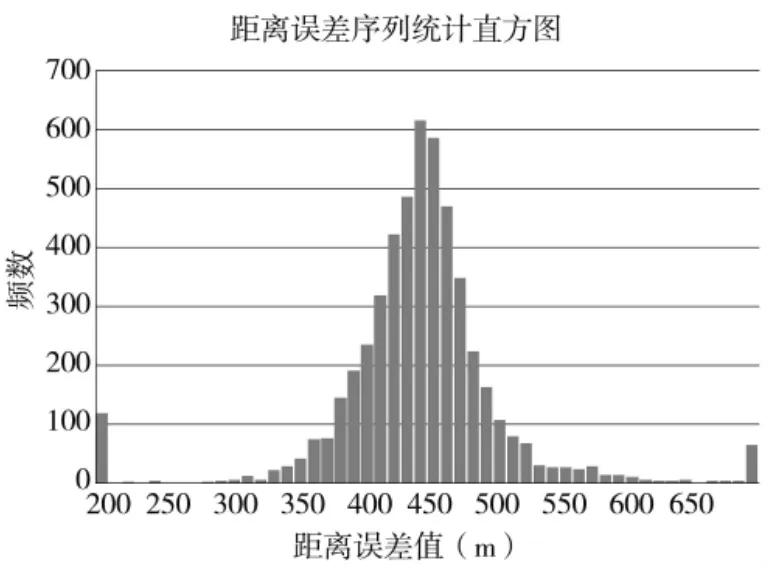
图2 筛选前距离误差统计序列统计直方图

首先对所有目标的距离误差序列对单个目标进行异常航迹的剔除，完成筛选后，共剔除168个异常样本，剩余样本共4 766个。完成异常值筛选的各目标误差序列散点图如图3所示。

图3 异常值筛选后距离误差序列散点分布图

这一步筛选可以将单目标误差序列中占少数的异常航迹进行剔除，因其对误差序列的标准差影响有限，可以通过区间筛选将其筛选并剔除；但对于目标密集区的目标，由于系统跟踪不稳定，或错误跟踪后纠正，如果这类航迹数量较多，对误差序列的标准差影响较大，仅通过区间筛选并不能将其筛选出来，如图3中的目标1和目标2，此时需要通过目标全航迹误差序列的检验，将其剔除。

下面进行错误关联目标的剔除。以图3中的目标3为例，该目标误差序列共n1=81个样本，均值 μ1=-337.66，方差 S21=2 749.01，剩余目标误差序列共n2=4 553个样本，均值μ2=433.61，方差S22=184 131.58，用公式

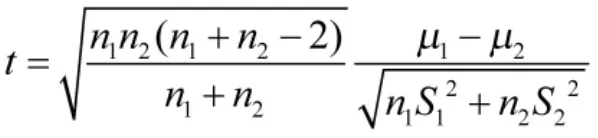
计算得到t=-16.17，在显著性水平为α=0.05下，，不能接受假设H0，判定该目标为错误关联目标，予以剔除；剔除所有错误关联目标后，剩余距离误差序列共4 504个点。完成剔除后的距离误差序列统计直方图如图4所示，各目标误差序列散点分布图如下页图5所示。

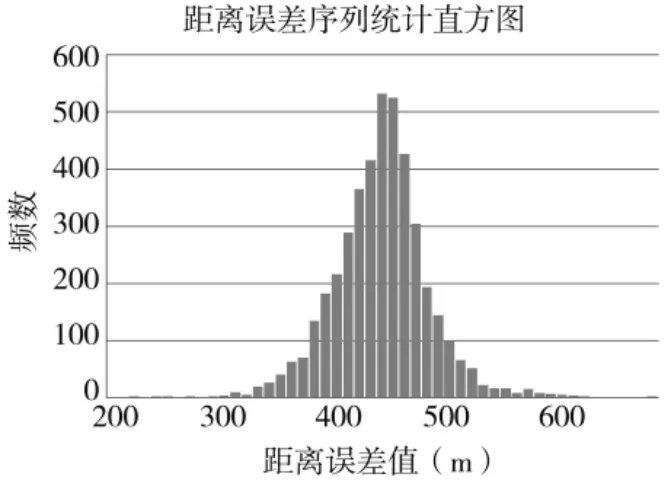
图4 错误目标剔除后距离误差序列统计直方图

图5 错误目标剔除后距离误差序列散点分布图

完成异常值筛选和错误目标剔除后，直方图分布相对集中，且较为符合正态分布的特征。

最后，对完成处理的距离误差序列计算均值，得到距离误差估计结果为偏大434.66 m。使用相同方法和流程处理方位误差序列，得到方位误差估计结果为偏大0.639°。

完成误差估计后，使用上述估计结果对雷达系统误差进行校准，再次进行数据采集实验，对校准结果进行验证。

验证实验的数据采集时间共76 min，共采集到该型雷达上报目标航迹共70批，AIS目标共1 674批；实现粗关联目标58对，完成异常值筛选和错误关联目标剔除后，剩余关联目标55对，有效距离误差序列为4 155个样本。校准后的距离误差序列统计直方图如图6所示，各目标误差序列散点分布图如图7所示。

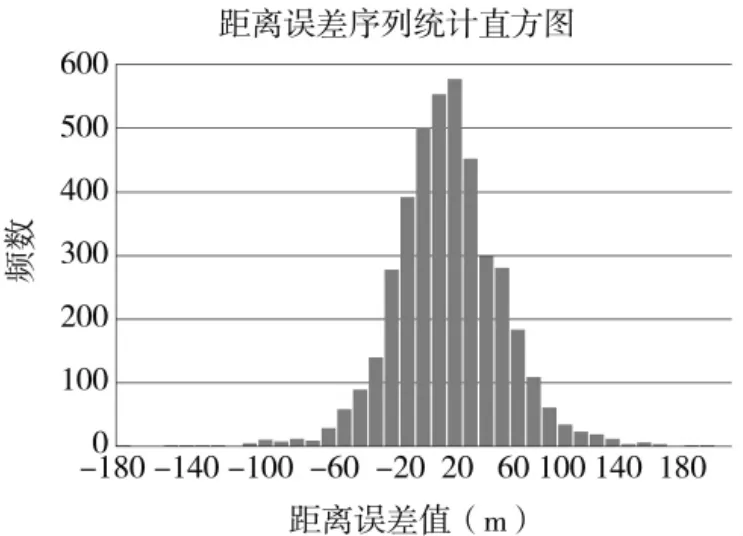
图6 校准后距离误差序列统计直方图

图7 校准后距离误差序列散点分布图

经计算，校准后雷达距离误差为偏大21.71 m，小于该型雷达距离分辨率，方位误差为偏大0.011°，小于该型雷达方位分辨率，达到了预期的校准效果。

4 结论

利用多目标信息进行联合误差估计的优势有：①各目标活动范围不一，能覆盖雷达主要探测区域，且目标运动形态各异，无需刻意对目标进行筛选，快慢速目标、机动目标、静止目标等均可以作为备选目标；②不同目标的AIS定位天线相对于船身的位置不一［12］，而雷达对目标的测量经凝聚后是回波的质心［13］，如使用单个目标进行估计，会引入天线位置带来的固定偏差，而使用多目标联合估计，可以显著消除不同类型船舶的定位天线位置不同带来的差异，减小该因素对估计结果的影响。

本文根据实践工作中积累的经验，应用提供高精度差分GPS定位数据的AIS作为标准设备，实现对海雷达的误差估计。首先实现系统误差条件下的航迹粗关联并完成航迹的时间对齐，再对误差序列分别进行单目标异常航迹筛选和错误关联目标的剔除，实现了对海雷达系统误差的估计。实际应用表明，该方法具有较好的校准效果，利用该方法已经实现XX部（套）对海雷达的误差校准工作。

［1］INCE A N.海上集成监视系统原理［M］.周沫，察豪，胡波，译.北京：电子工业出版社，2012.

［2］汪洋，罗军.五种常用航迹关联算法在AIS与岸对海警戒雷达航迹关联中的仿真分析［J］.论证与研究，2010（3）：23-26.

［3］陈林元，何佳洲，罗双喜.多目标环境下分布未知的系统误差估计方法研究［J］.计算机与数字工程，2013，41（3）：382-387.

［4］刘冬利，何民，张驿，等.一种新的岸海警戒雷达标校方法［J］.电讯技术，2009，49（6）：53-56.

［5］赵永刚.一种岸海警戒雷达的标校方法［J］.现代电子技术，2012，35（9）：22-24.

［6］罗军，商允力，曾浩，等.应用AIS信息进行岸基对海雷达标校［J］.电讯技术，2009，49（9）：87-89.

［7］汪洋，罗军.基于AIS的岸对海警戒雷达系统误差误差校准方法研究［J］.论证与研究，2011，1：26-28.

［8］潘绍仁，察豪.基于AIS的舰载雷达标校方法研究［J］.舰船科学技术，2009，31（6）：101-104，127.

［9］刘熹，尹浩，吴泽民，等.无先验关联的雷达系统误差协同配准算法［J］.西安电子科技大学学报（自然科学版），2013，40（5）：26-32，140.

［10］田威，王钺，山秀明，等.稳健的联合航迹关联与系统误差估计［J］.清华大学学报（自然科学版），2013，53（7）：946-950.

［11］朱起悦.应用差分GPS技术进行雷达标校［J］.电讯技术，2006，46（1）：108-110.

［12］吴顺君，梅晓春.雷达信号处理和数据处理技术［M］.北京：电子工业出版社，2008.