基于压缩传感的PSO-OMP重构算法的研究*

王红云，王 鹏，张 楠，白艳萍

（中北大学理学院，太原 030051）

基于压缩传感的PSO-OMP重构算法的研究*

王红云，王 鹏，张 楠，白艳萍

（中北大学理学院，太原 030051）

由于粒子群算法具有解决寻优问题的能力，将其应用于信号处理领域，提出了一种新的基于PSO-OMP的信号重构算法。为了降低计算复杂度，把粒子群算法运用在正交匹配追踪算法的匹配过程，以此来确定最优原子。实验结果表明，所提出的新的基于PSO-OMP的信号重构算法具有计算复杂度低和重构成功概率高等特点。

压缩传感，重构算法，正交匹配追踪算法，粒子群算法

Abstract：Because the particle swarm algorithm has the ability to solve the problem of optimization，applied to the field of signal processing，this paper proposes a new signal reconstruction algorithm based on PSO-OMP.In order to reduce the computational complexity，the particle swarm algorithm is used in matching process of orthogonal matching pursuit algorithm，in order to determine the optimal atom.The experimental results show that the proposed new signal reconstruction based on PSO-OMP algorithm has low computing complexity and reconstruct high success probability.

Key words：compressed sensing，reconstruction algorithm，orthogonal matching pursuit algorithm，particle swarm optimization algorithm

0 引言

近年来，由于信号的采样一直受到Nyquist采样定理即信号的采样频率必须比信号最高频率的二倍高的限制，这对信号提出了很高的要求。然而，在实际应用中，为了减少采样的时间，提高采样的效率，人们被迫去寻找新的采样方式，这样，压缩传感［1-2］就被提出了，它主要是对稀疏或可压缩信号进行投影，通过采集少部分的信号投影值，利用与其对应的重构算法由传感矩阵获得原始信号的过程。

在压缩传感中，重构算法成为其关键的组成部分，它主要涉及压缩信号精确重构的概率和效果。目前，重构算法有很多种，分别是：匹配追踪（MP）［3］、正交匹配追踪（Orthogonal Matching Pursuit，OMP）［4］、正则化正交匹配追踪（ROMP）［5］、压缩采样匹配追踪（CoSaMP）［6］、分段正交匹配（StOMP）［7］、分段弱正交匹配（SWOMP）［8］和广义正交匹配（gOMP）［9］。其中应用最广泛的是OMP算法，收敛快且精度高。然而，对在过完备原子库上的重构问题，OMP算法的匹配过程需要对原子库中全部的原子进行遍历，而过完备原子库中原子过多使得计算复杂度较高。粒子群优化（Particle Swarm Optimization，PSO）［10］是一种启发式的全局搜索算法，它主要通过迭代寻找全局最优解，本文将PSO算法用于OMP算法的匹配过程，来提高搜索最优原子的能力。因此，提出了新的基于PSO-OMP的信号重构算法，与OMP算法相比，不仅减少了计算内积的次数，而且提高了信号重构成功概率。

1 基本理论

1.1 压缩传感理论

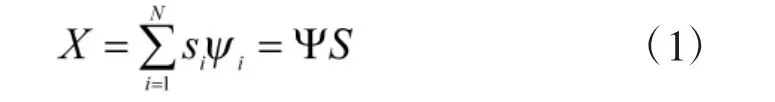
式中，si为展开系数，记为向量形式若展开系数中的非零分量的个数越少，则说明其越稀疏。如果展开系数S中非零元素的个数为K，则信号X在Ψ的稀疏度为K。对信号X利用一个大小为M×N维的投影测量矩阵Φ（M＜N）进行线性测量，获得长度为M的观测信号为y：

式中，Θ=ΦΨ称为传感矩阵。在有限等距性（RIP）的前提下，即其可以用公式表示为：

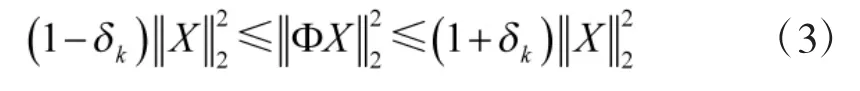
1.2 正交匹配追踪算法

OMP算法中的核心思想是：首先将传感矩阵Θ看作一个过完备原子库，从中选出与信号残差最相关的原子，对其进行Gram-Schmidt正交化处理，然后利用当前信号残差减去在原子上的相关部分作为下一次迭代的信号残差，最后对迭代停止的条件进行判断，即迭代次数达到稀疏度K。

OMP算法对信号重构的步骤如下：

1）对信号残差进行初始化使r0=y，为传感矩阵Θ中的所有原子建立索引集，迭代次数n=0；

2）计算信号残差rn-1和传感矩阵Θ中原子的内积；

3）寻找内积向量gn中绝对值最大的，对与其相对应的脚标进行索引，使得；

7）对迭代次数进行更新，使得n=n+1，若n＞K，则输出重构信号Sn和信号残差rn；否则，返回到步骤2）；

8）最后根据式（1）得到原始信号X。

1.3 粒子群算法

PSO算法是一种启发式进化算法，其思想来源于鸟群在空中觅食的过程，即把每只鸟作为一个独立的个体，并且根据群体中当前距离目标最近位置的个体和自身最优位置去确定下一步的搜索方向和速度大小，以此来最快获得目标的位置，利用这种特征来求解函数优化问题，其中每个独立的个体被抽象为一个粒子，代表优化问题的一个候选解，被用位置和速度向量来表示，每个候选解能根据适应度函数得到适应度值。PSO算法的更新公式为：

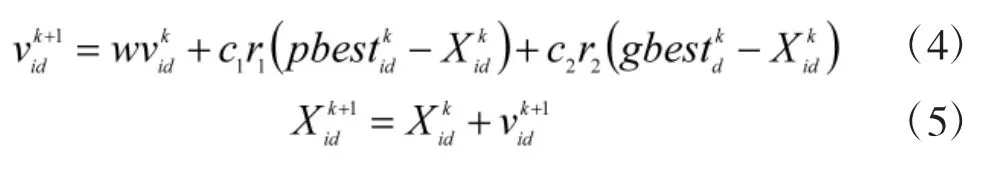
式中，w为惯性权重；c1和c2为学习因子；r1和r2都是区间［0，1］的一个随机数，分别表示自身体验和社会经验的影响因素。分别表示第i个粒子在k次迭代中第d维的速度和位置表示第i个粒子在第d维的个体最优的位置表示种群在第d维的全局最优的位置。

2 改进的PSO-OMP算法

在过完备原子库的压缩传感中，OMP算法的匹配过程需要遍历原子库中所有原子，而过完备原子库中原子过多使得计算复杂度较高。本文利用PSO对OMP的匹配过程进行优化，使其快速收敛到全局最优。选择OMP的匹配函数作为PSO的适应度函数：

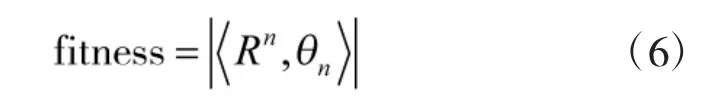
2.1 算法实现

本文提出的基于PSO-OMP算法的步骤可总结如下：

1）对信号残差进行初始化使R0=y，设定最优原子的集合为，迭代次数n=1；

2）初始化所有粒子，设置PSO算法的参数，确定 pbest和 gbest；

3）对粒子的速度根据式（4）进行更新，判断粒子的速度是否满足速度的要求，若不满足，则用边界值代替，再对粒子的位置根据式（5）进行更新；

4）对每个粒子的适应度值根据式（6）进行计算，更新 pbest和 gbest；

5）对粒子群更新代数进行判断是否达到最大，若是，则输出gbest，gbest就是本次搜索的最优原子；若不是，重复步骤2）～4），继续搜索直到找到最优原子；

9）对迭代进行判断，若n≤K，则n=n+1，重复步骤2）～8）；否则，输出重构信号Sn和信号残差Rn；

10）最后按照式（1）得到原始信号X。

2.2 仿真与结果分析

为了对PSO-OMP算法验证，本文基于window下的MATLAB仿真环境实现了PSO-OMP算法，并与原始的OMP进行性能的比较。

仿真实验采用的是长度为N=256的一维信号，稀疏度 K=10，观测信号长度为 64，投影测量矩阵为高斯随机矩阵，采样点数是由公式确定的。而优化算法种群的数量为sizepop=256，粒子的最大搜索次数t=10。

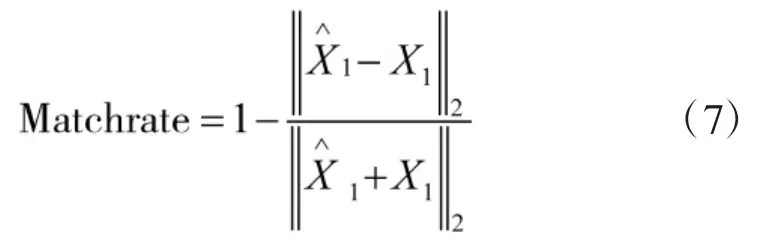
式（7）的取值在［0，1］之间，它表示信号重构的效果。其值越大，说明信号的重构能力越强，效果越好；其值越小，说明信号的重构能力越弱，效果越差。相反，信号的相对误差为：

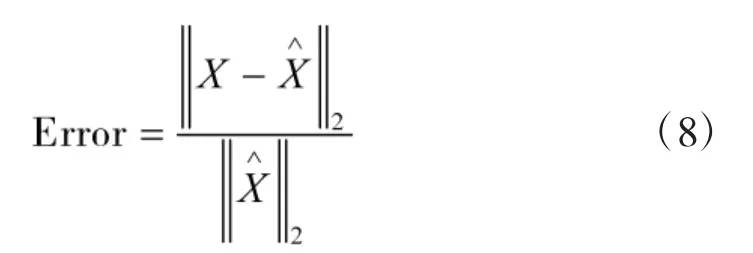
式（8）说明其值越大，信号重构的质量越差；其值越小，信号重构的质量越好。

OMP算法与PSO-OMP算法对原始信号的重构可以从图1看到。而两种算法对信号重构的匹配率和相对误差的结果利用式（7）和式（8）计算所得，它们的对比结果如表1所示，从表1观察可得，基于PSO-OMP算法的匹配率相对较高，其相对误差较小，内积计算次数也较少使得计算复杂度降低。

图1 两种算法对原始信号的重构

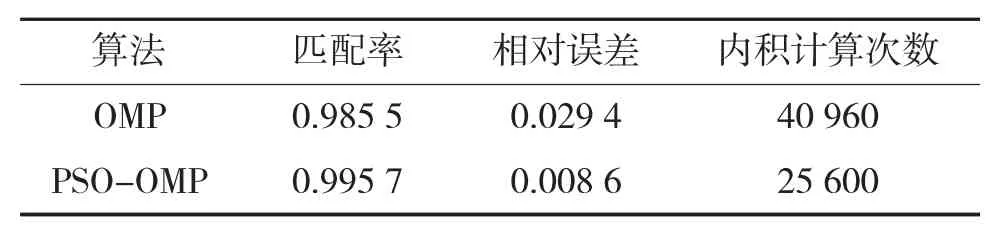
表1 OMP算法与PSO-OMP算法重构结果的对比

为了更加充分表现PSO-OMP算法的优越性，以信号的重构概率为指标，对OMP算法和PSO-OMP算法分别进行了在不同观测值M和不同稀疏度K的条件下的比较，其结果分别如图2和图3所示。从图2可以看出，观测值M较小时，两种方法的重构概率基本相同，但随着观测值M的增加，PSO-OMP的重构概率逐渐高于OMP，且PSO-OMP的重构概率相对比较稳定。

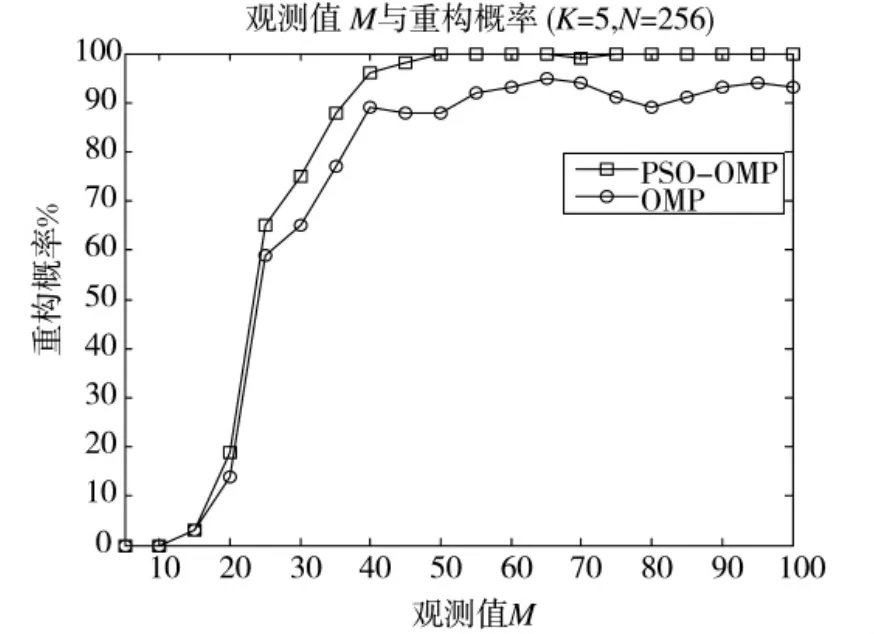
图2 不同观测值下两种算法重构概率的比较

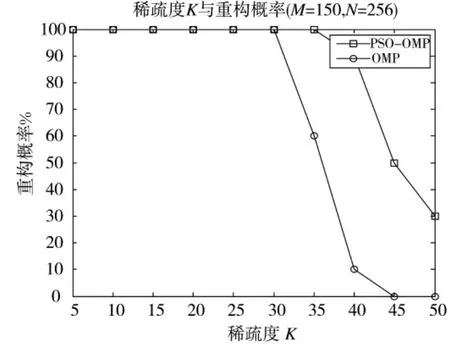
图3 不同稀疏度下两种算法重构概率的比较

从图3观察得到，两种方法的重构概率随着稀疏度K的增大而减小，在稀疏度K逐渐增大的过程中，PSO-OMP的重构概率明显高于OMP，且在稀疏度K为45°时，PSO-OMP的重构概率为30%，而OMP为0。但是，当稀疏度K不大于30时，两种方法的重构概率值都最大，都为100%。

3 结论

对于稀疏或可压缩信号，压缩传感采样比Nyquist采样更加有用且实用范围广。在压缩传感中，信号重构成为其关键部分，主要包括信号的重构概率和效果。然而，针对OMP算法的计算复杂度较高，本文提出了一种新的基于PSO-OMP的信号重构算法。实验结果表明，所提出的基于PSO-OMP的信号重构算法与原始的OMP算法相比，不仅可以降低计算复杂度，而且可以提高重构成功概率。然而每种算法都有局限性，即基于PSO-OMP的信号重构算法有随机性的缺点。因此，下一步的工作是寻找更稳定的信号重构算法。

［1］DONOHO D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1289-1306.

［2］CANDES E J，TAO T.Near optimal signal recovery from randomprojections：universalencodingstrategies［J］.IEEETransactionsonInformationTheory，2006，52（12）：5406-5425.

［3］MALLAT S，ZHANG Z.Matching pursuits with time-frequency dictionaries［J］.IEEE Transactions on Signal Processing，1993，41（12）：3397-3415.

［4］TROPP J，GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53（12）：4655-4666.

［5］NEEDELL D，VERSHYNIN R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit［J］.Found Comput Math，2009，9（3）：317-334.

［6］NEEDELL D，TROPP J A.CoSaMP：Iterative signal recovery from incomplete and inaccurate samples［J］.Communi-Cations of The ACM，2010，53（12）：93-100.

［7］DONOHO D L，TSAIG Y，DroriI，te al.Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2012，58（2）：1094-1121.

［8］BLUMENSATH T，DAVIES M E.Stagewise weak gradient pursuits ［J］.IEEE Transactionson SignalProcessing，2009，57（11）：4333-4346.

［9］WANG J，KWON S，SHIM B.Generalized orthogonal matching pursuit［J］.IEEE Transactions on Signal Processing，2011，60（12）：6202-6216.

［10］KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proceedings of 1995 IEEE International Conference on Neural Networks.Perth，Australia：IEEE，1995，1942-1948.

PSO-OMP Reconstruction Algorithm Based on Compressed Sensing

WANG Hong-yun，WANG Peng，ZHANG Nan，BAI Yan-ping
（School of Science，North University of China，Taiyuan 030051，China）

TP301

A

10.3969/j.issn.1002-0640.2017.09.005

1002-0640（2017）09-0021-04

2016-05-11

2016-07-09

国家自然科学基金（61275120）；山西省回国留学人员科研基金资助项目（2016-088）

王红云（1992- ），女，山西朔州人，硕士研究生。研究方向：智能计算与信息处理。