一种脉冲超宽带测控信号捕获方法

廉 昕 王元钦 侯孝民 孟祥利



一种脉冲超宽带测控信号捕获方法

廉 昕*王元钦 侯孝民 孟祥利

(装备学院 北京 101416)

脉冲超宽带测控系统作为一种航天测控新体制，可有效提高系统的隐蔽性和抗干扰性。该文针对脉冲超宽带测控信号的捕获问题，提出利用基于部分匹配滤波与快速傅里叶变换(Partial Matched Filtering and Fast Fourier Transform, PMF-FFT)的捕获方法完成对脉冲相位、伪码相位和多普勒频率的3维捕获。又针对搜索空间大、捕获时间长和多普勒频率估计精度低的问题，提出了一种改进的捕获方法。该方法采用两步捕获法对时延相位进行捕获，同时利用修正的Rife算法对多普勒频率进行进一步精细估计。仿真结果表明，该方法可有效提高捕获速度，减小捕获时间，且能显著提高多普勒频率估计精度。

脉冲超宽带；测控；捕获；多普勒频率；Rife算法

1 引言

随着航天技术的发展，世界各国在航天领域的竞争日趋激烈。航天测控通信系统是执行航天活动的重要支撑和保障，其安全性越来越受到重视。而现行测控系统的隐蔽性和抗干扰性仍存在不足，难以满足未来航天测控系统的需求[1]。脉冲超宽带技术是一种利用极窄脉冲作为载体进行信息传输的无线通信技术。将脉冲超宽带技术引入到航天测控系统中，构建脉冲超宽带测控新体制，可大大提高测控系统的隐蔽性和抗干扰能力，同时还可提高测距精度、增大系统容量[2]。

脉冲超宽带系统目前主要用于室内短距离的高速数据传输和高精度测距定位，对信号的同步捕获是系统的关键环节之一。目前对其信号捕获方法的研究大多集中在室内复杂密集多径环境下的时延捕获。由于脉冲超宽带信号的脉冲宽度很窄，且具有一定的占空比，导致其搜索空间巨大，从而增大了信号捕获的难度[3]。文献[4-6]等从搜索策略的角度出发，提出了观察再跳K单元搜索、比特反转搜索等高效搜索策略，以实现对信号的快速捕获。文献[7,8]等提出了两步捕获法，对整个搜索空间进行分阶段搜索，可有效缩短捕获时间，同时保证较高的捕获精度。

然而，以上方法只针对信号时延的捕获，并未考虑信号在传输过程中的动态变化。而对于脉冲超宽带测控系统，由于测量目标为高速飞行的航天器，在信号传输过程中还会产生一定的多普勒效应。因此，对脉冲超宽带测控信号的捕获包括对信号时延和多普勒频率的2维捕获。对测控信号的成功捕获是测距测速功能得以实现的必要条件，也是后续数据解调的前提。

本文针对脉冲超宽带测控信号，采用基于部分匹配滤波与快速傅里叶变换(PMF-FFT)的信号捕获方法，可同时对信号时延和多普勒频率进行捕获。又针对捕获时间长、多普勒频率估计精度低等问题，对原捕获方法进行改进，提出了一种基于改进PMF-FFT的信号捕获方法，并对所提方法进行仿真验证和性能分析。

2 信号模型

脉冲超宽带测控系统采用载波调制的直接序列扩频-脉冲幅度调制(DS-PAM)信号，该信号首先对数据信息进行伪码扩频调制，所得调制码再对矩形窄脉冲串进行脉冲幅度调制，最后进行Ka频段载波调制。其信号表达式为[9,10]

在脉冲超宽带测控系统中，由于地面测站与航天器之间存在高速的相对运动，信号在传播过程中会产生多普勒效应，设其载波多普勒频率为。同时假设测控信道为加性高斯白噪声信道，则接收机接收到的信号经下变频和滤波后的表达式为

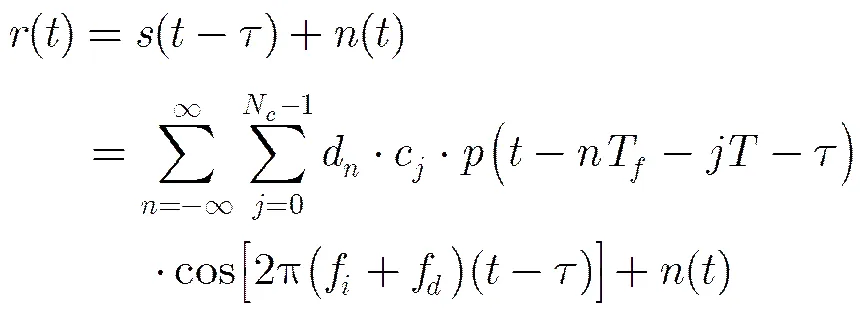
对接收信号的同步捕获通常利用相关处理的方法，即将本地产生的模板信号与接收信号进行相关运算：

(4)

当本地模板信号与接收信号的时延相位和载波频率均完全一致时，其相关运算结果达到最大峰值。

3 基于PMF-FFT的捕获方法

在直接序列扩频测控系统中，通常采用基于PMF-FFT的方法对信号进行伪码-多普勒的2维捕获[11,12]。该方法将本地模板信号与接收信号进行部分相关，再利用FFT运算进行多普勒补偿。鉴于脉冲超宽带测控信号与直扩信号的相似性，对现有PMF-FFT捕获方法进行适当调整，即可应用于脉冲超宽带测控信号的捕获。该方法的原理框图如图1所示。

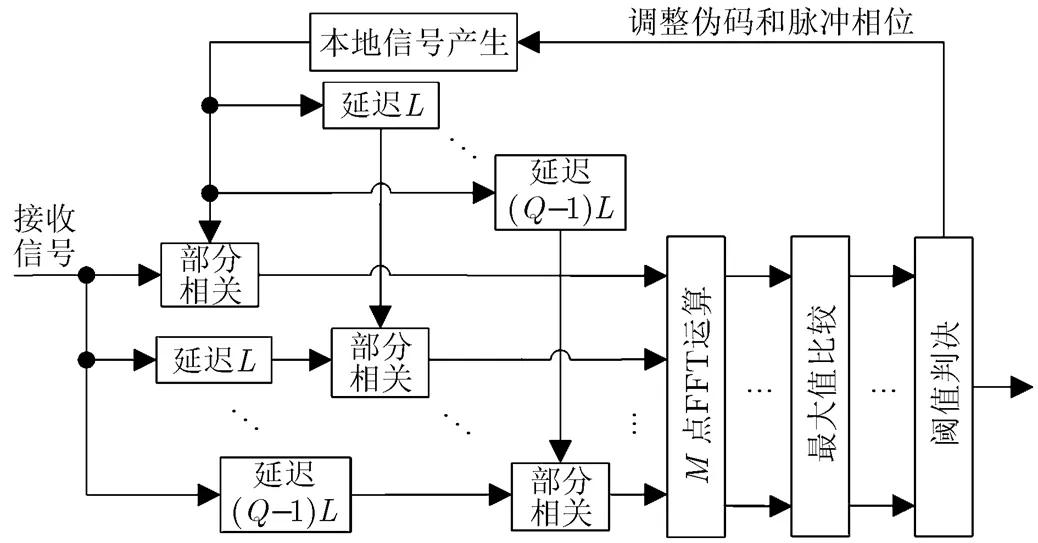
图1 基于PMF-FFT的信号捕获方法

图2 不同Q 值下的归一化相关峰值

以上方法考虑了多普勒频移对相关结果的影响，利用FFT运算进行频率补偿，实现了时延和多普勒频率的2维捕获[13]。但对于脉冲超宽带测控信号，其时延相位的搜索空间巨大。若搜索步长为一个脉冲宽度，则其搜索空间的大小为伪码码长与脉冲占空比倒数的乘积，即。采用串行搜索策略，由于一次相关时间为，则其最长捕获时间为。而对于多普勒频率的捕获，若信号采样率为, FFT运算点数为，则其频率分辨率为，即最大频率估计误差为。

4 基于改进PMF-FFT的捕获方法

由以上分析可知，对于脉冲超宽带测控信号，直接采用基于PMF-FFT的捕获方法所面临的问题主要有：一是由于信号时延相位包括伪码相位和脉冲相位，其搜索空间大，捕获时间长；二是由于信号带宽很宽，所需采样率很高，而FFT点数有限，使得多普勒频率估计精度较低。针对以上问题，在原PMF-FFT捕获方法的基础上进行改进。

4.1基于两步捕获法的信号时延捕获

为了快速减小时延相位搜索空间，提高捕获速度，可采用两步捕获法分别对脉冲相位和伪码相位进行捕获，同时还可考虑与原PMF-FFT法相结合。故这里采取先捕获脉冲相位，再采用PMF-FFT的方法对伪码相位和多普勒频率进行捕获的策略。

对于脉冲相位的捕获，可采用简单的并行搜索策略，如图3所示，其搜索步长为一个脉冲宽度。

图3 脉冲相位捕获方案

在完成脉冲相位的捕获后，采用PMF-FFT的方法对伪码相位和多普勒频率进行2维捕获，其处理过程与图1所示相同，只是本地模板信号的脉冲相位固定，每次相位调整的步长为一个伪码宽度，其搜索空间大小仅为。

以上基于两步捕获法的改进算法大大提高了对信号时延相位的捕获速度，有效缩短了捕获时间。

4.2 基于修正Rife算法的频率估计

为了提高PMF-FFT捕获方法的多普勒频率估计精度，可采用Rife算法加以改进。Rife算法是Rife等人[14]提出的一种计算量小、估计精度高的频率估计方法。该方法在进行FFT运算后，在FFT输出结果的最大值和次大值之间，利用插值的方法对信号频率进行精细估计。Rife算法的基本计算公式为

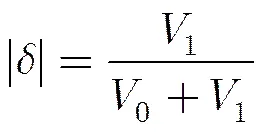
由于在PMF-FFT捕获方法中也采用了FFT运算，故可利用Rife算法对多普勒频率进行精细估计。假设伪码码长分段数FFT点数，且本地模板信号与接收信号的时延相位已完全对齐，则当多普勒频率变化时，FFT运算结果的最大值和次大值以及式(5)中的值如图4所示。

由图4可知，FFT运算结果随多普勒频率呈周期性变化。图4(b)中的最大值出现在FFT相邻量化频率的中点，而其最小值出现在FFT各量化频率上。在一个量化频率范围之内，值随多普勒频率呈线性变化。根据值与多普勒频率的关系，需对原Rife算法公式进行修正。利用最小二乘法进行曲线拟合，可得修正的坐标偏移量与FFT最大值和次大值之间的关系表达式：

图4 FFT运算结果与多普勒频率的关系

因此，在进行基于PMF-FFT的信号捕获过程中，可根据FFT输出结果的最大值和次大值，利用式(7)和式(6)对多普勒频率进行精细估计，以减小频率估计误差。

4.3整体捕获方案

综合以上两点改进，提出基于改进PMF-FFT的信号捕获方案，其整体实现框图如图5所示。

首先，利用并行搜索策略对脉冲相位进行捕获，搜索步长为一个脉冲宽度。之后，利用捕获到的脉冲相位，采用PMF-FFT的方法对伪码相位和多普勒频率进行2维捕获。当FFT运算结果最大值超过阈值时，判定捕获成功，此时本地信号的脉冲相位、伪码相位和多普勒频率即为捕获结果。同时，利用修正Rife算法对多普勒频率进行精细估计，以进一步提高频率估计精度。

该方法可完成对脉冲相位、伪码相位和多普勒频率的3维捕获，减小了相位搜索空间，从而提高了捕获速度。同时提高了多普勒频率的估计精度，为后续对信号的精密跟踪奠定了基础。

5 仿真分析

现对本文提出的基于改进PMF-FFT的脉冲超宽带测控信号捕获方法进行仿真分析。信号参数如下：伪码码长，码速率，脉冲占空比1/8，中频载波频率。信号经过高斯白噪声信道，信噪比，传输时延，多普勒频率。采用本文所提方法对信号进行捕获，令PMF分段数FFT点数，则信号捕获结果如图6所示。

5.1捕获精度

下面对本文方法在不同条件下的捕获精度进行仿真分析。由于对时延相位的搜索步进为1个脉冲宽度，故其对时延的估计误差最大为，这与原PMF-FFT捕获方法相同。这里重点分析多普勒频率的估计精度。假设信号参数不变，且本地模板信号与接收信号的时延相位已完全对齐，则当接收信号的多普勒频率变化时，两种捕获方法的多普勒频率估计结果如图7所示。

图5 基于改进PMF-FFT的信号捕获方案

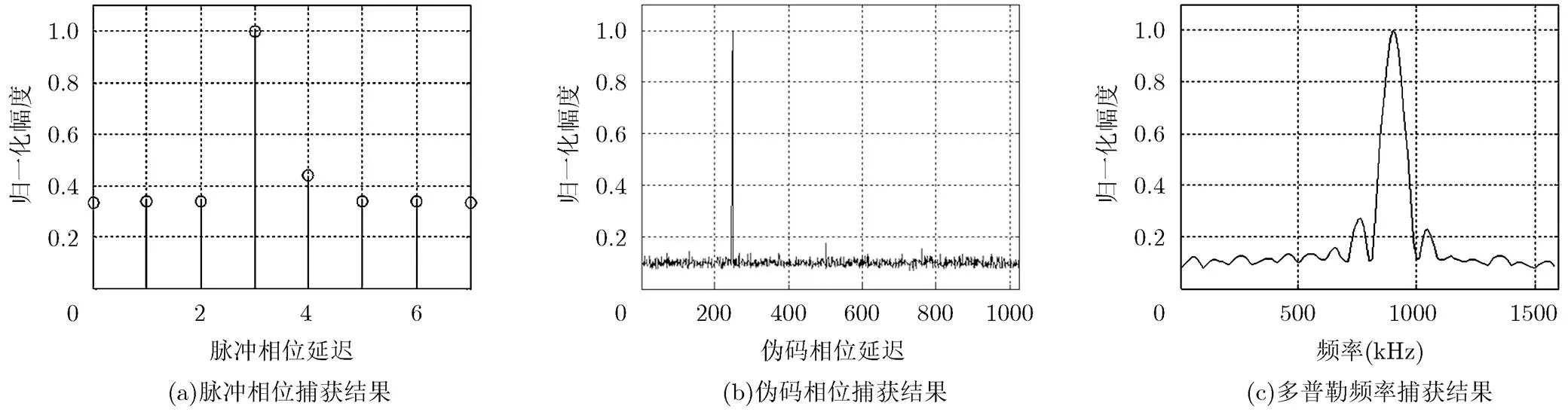
图6 基于改进PMF-FFT法捕获结果

可见，由于FFT点数有限，导致PMF-FFT捕获方法的频率分辨率较低，多普勒频率捕获误差较大，其最大频率误差达。而利用修正Rife算法对原方法进行改进，可显著提高多普勒频率捕获精度，其最大频率误差在以下，为后续的载波跟踪环节提供了方便。

图7 两种捕获方法的多普勒频率估计误差

5.2捕获性能

由图8可见，在判决阈值固定不变的情况下，两种捕获方法的捕获概率均随信噪比的增大而增大，而虚警概率均随之减小。由于本文方法在第1步对脉冲相位进行捕获时采用了非相干累加，其累加效果要比相干累加差，导致其捕获性能与原PMF-FFT法相比有所下降。

由捕获概率和虚警概率即可得到捕获方法的平均捕获时间。一般将捕获过程看作是一个离散时间有限状态的马尔可夫过程，则PMF-FFT法的平均捕获时间为[11]

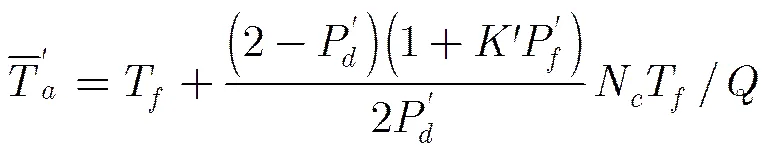
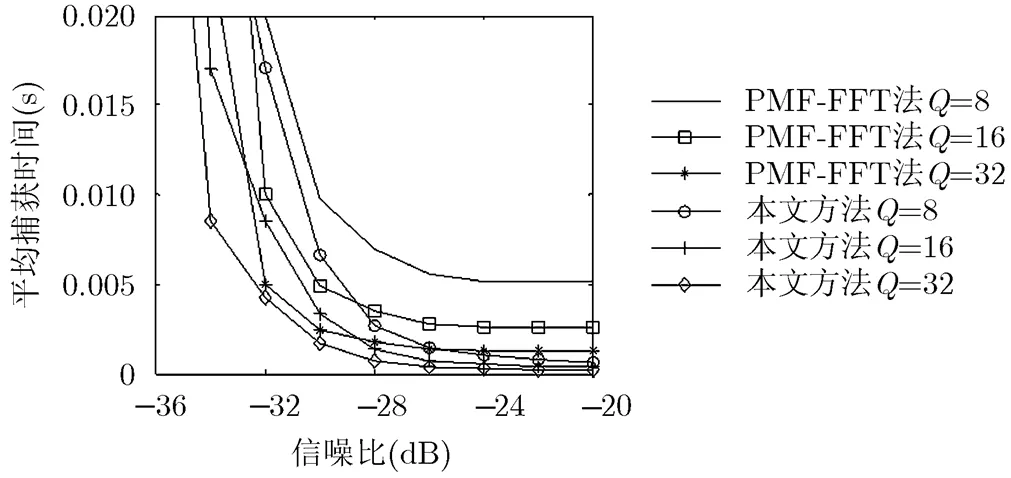
图9 两种捕获方法的平均捕获时间

可见，与原PMF-FFT法相比，本文提出的改进方法由于采用了两步捕获法进行时延相位捕获，在分段数相同的情况下，其平均捕获时间明显更短，有效提高了捕获速度。此外，两种捕获方法的平均捕获时间均随分段数的增大而减小，因此可通过增大来缩短信号捕获时间。

6 结论

本文首先建立了脉冲超宽带测控信号模型，采用基于PMF-FFT的捕获方法对信号进行捕获。又针对时延相位搜索空间大、捕获时间长和多普勒频率捕获精度低的问题，提出了一种基于改进PMF- FFT的信号捕获方法。该方法采用两步捕获法对时延相位进行捕获，并利用修正Rife算法对多普勒频率进行精细估计。仿真结果表明，本文方法可完成对脉冲超宽带测控信号的脉冲相位、伪码相位和多普勒频率的3维捕获。且该方法能有效缩短信号捕获时间，提高多普勒频率的估计精度。其缺点是由于采用了非相干累加导致其捕获概率性能与原PMF-FFT法相比有所下降。

[1] 雷厉, 朱勤专. 飞行器测控通信技术发展趋势与建议[J]. 飞行器测控学报, 2014, 33(6): 463-468. doi: 10.7642/j.issn. 1674-5620.2014-06-0463-06.

LEI Li and ZHU Qinzhuan. Analysis of the trend of development of spacecraft TT&C and communication technologies and suggestions[J]., 2014, 33(6): 463-468. doi: 10.7642/j.issn.1674- 5620.2014-06-0463-06.

[2] WANG F, ZHANG X, WANG F,. Joint estimation of TOA and DOA in IR-UWB system using a successive propagator method[J]., 2015, 102(10): 1765-1788. doi: 10.1080/00207217.2014. 996781.

[3] AEDUDODLA S R, VIJAYAKUMARAN S, and WONG T F. Timing acquisition in ultra-wideband communication systems[J]., 2005, 54(5): 1570-1583. doi: 10.1109/TVT.2005.855495.

[4] JOUNG Y B, CHONG D, YOON S,. A generalized analysis for search strategies in UWB signal acquisition[C]. International Conference on Advanced Communication Technology, Gangwon-Do, Korea, 2007, 612-614. doi: 10.1109 /ICACT.2007.358430.

[5] HOMIER E A and SCHOLTZ R A. Rapid acquisition of ultra-wideband signals in the dense multipath channel[C]. 2002 IEEE Conference on Ultra Wideband Systems and Technologies, Baltimore, MD, USA, 2002, 105-109. doi: 10.1109/UWBST.2002.1006329.

[6] VIJAYAKUMARAN S and WONG T F. A search strategy for ultra-wideband signal acquisition[J]., 2015, 53(12): 2015-2019. doi: 10.1109 /TCOMM.2005.860074.

[7] SAGHAFI A and FAKHRAIE S M. A new search space reduction technique for acquisition of UWB signals in multipath channels[C]. 2007 IEEE 65th Vehicular Technology Conference, Dublin, Ireland, 2007: 1559-1563. doi: 10.1109/ VETECS.2007.325.

[8] IBRAHIM J and BUEHRER R M. Two-stage acquisition for UWB in dense multipath[J]., 2006, 24(4): 801-807. doi: 10.1109/JSAC. 2005.863832.

[9] CONROY J T, LOCICERO J L, and UCCI D R. Communication techniques using monopulse waveforms[C]. IEEE Military Communications Conference 1999, Atlantic City, NJ, USA, 1999: 1181-1185. doi: 10.1109/MILCOM.1999. 821389.

[10] 廉昕, 王元钦, 侯孝民, 等. 脉冲超宽带信号测量性能分析[J].飞行器测控学报, 2015, 34(5): 427-437. doi: 10.7642/j.issn. 1674-5620.2015-04-0427-11.

LIAN Xin, WANG Yuanqin, HOU Xiaomin,. Analysis of the measuring performance of UWB signals[J].&, 2015, 34(5): 427-437. doi: 10.7642/j.issn.1674-5620.2015-04-0427-11.

[11] SPANGENBERG S M, SCOTT I, MCLAUGHLIN S,. An FFT-based approach for fast acquisition in spread spectrum communication systems[J]., 2000, 13(1): 27-56. doi: 10.1023/A: 1008848916834.

[12] QI J, LUO F, and SONG Q. Fast acquisition method of navigation receiver based on folded PMF-FFT[C]. Proceedings of 2014 IEEE Computing, Communications and IT Applications Conference, Beijing, China, 2014: 62-66. doi: 10.1109/ComComAp.2014.7017171.

[13] MA Y, SUN H, and YUAN W. BDS/GPS satellite signal acquisition algorithm research based of PMF (Partial Matched Filter) and FFT[C]. 2015 International Conference on Network and Information Systems for Computers (ICNISC), Wuhan, China, 2015: 194-196. doi: 10.1109/ ICNISC.2015.38.

[14] RIFE D C and VINCENT G A. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J]., 1970, 49(2): 197-228. doi: 10.1002/j.1538-7305.1970.tb01766.x.

[15] LIU X, REN Y, CHU C,. Accurate frequency estimation based on three-parameter sine-fitting with three FFT samples[J].&, 2015, 22(3): 403-416. doi: 10.1515/mms-2015-0032.

[16] 刘晓明, 张鹤, 吴皓威, 等. 高动态环境下长码扩频信号快捕算法[J]. 电子与信息学报, 2016, 38(6): 1398-1405. doi: 10. 11999/JEIT150860.

LIU Xiaoming, ZHANG He, WU Haowei,. Rapid DSSS signal acquisition algorithm under high dynamic environment [J].&, 2016, 38(6): 1398-1405. doi: 10.11999/JEIT150860.

[17] 冯文全, 刘曦, 李春升. 扩频测控体制信号捕获方法分析[J]. 北京航空航天大学学报, 2013, 39(9): 1150-1156.

FENG Wenquan, LIU Xi, and LI Chunsheng. Analysis on acquisition method in spread spectrum TT&C system[J]., 2013, 39(9): 1150-1156.

Acquisition Scheme for Impulse Radio UWB TT&C Signal

LIAN Xin WANG Yuanqin HOU Xiaomin MENG Xiangli

(,101416,)

The impulse radio Ultra-WideBand (UWB) Tracking, Telemetry, and Command (TT&C) system is a new kind of TT&C system that can greatly improve the concealment and anti-interference performance. To solve the acquisition problem of the impulse radio UWB TT&C signal, an acquisition scheme based on Partial Matched Filtering and Fast Fourier Transform (PMF-FFT) is proposed to accomplish the three-dimensional acquisition of pulse phase, pseudorandom code phase and Doppler frequency simultaneously. Then, according to the problem of excessive search space, long acquisition time and low estimation accuracy of Doppler frequency, a new improved acquisition scheme is proposed. It adopts the two-step scheme to accomplish time delay phase acquisition, and uses the modified Rife algorithm to further estimate the Doppler frequency. Simulation results show that this scheme can effectively improve the acquisition speed, reduce the acquisition time, and greatly improve the estimation accuracy of Doppler frequency.

Impulse radio UWB; Tracking, Telemetry, and Command (TT&C); Acquisition; Doppler frequency; Rife algorithm

TN911.3

A

1009-5896(2017)08-2000-07

10.11999/JEIT161213

2016-11-09；

改回日期：2017-02-08；

2017-05-02

廉昕 lianxin20032002@aliyun.com

廉 昕： 男，1987年生，博士生，研究方向为航天测控技术、脉冲超宽带技术.

王元钦： 男，1963年生，教授，博士，研究方向为航天测控系统、高速数字信号处理.

侯孝民： 男，1968年生，教授，博士，研究方向为航天测控系统、高速数字信号处理.

孟祥利： 男，1991年生，硕士生，研究方向为航天测控技术、脉冲超宽带技术.