基于KL散度的雷达信号波形抗截获性能评估

王旭东 陆 威 闫 贺



基于KL散度的雷达信号波形抗截获性能评估

王旭东 陆 威*闫 贺

(南京航空航天大学电子信息工程学院 南京 211106)

该文给出了一种对13类常用雷达信号波形的抗截获性能进行评价的新方法，可为雷达波形的设计者提供评价波形抗截获性能的一般性准则。该准则假定白噪声信号具有最好的抗截获性能，通过将不同雷达信号波形和白噪声信号进行比较，得出雷达信号和白噪声的相似程度。首先，利用Wigner半圆法推出白噪声和雷达信号的特征分布函数，然后用KL散度来表示雷达信号和白噪声之间的相似性，较小的KL散度值，意味着较强的抗截获性能，反之亦然。理论推导和仿真验证表明这种评价准则可对不同雷达信号波形的抗截获性能进行有效评价。

雷达信号波形；抗截获性能；评价准则；KL散度；Wigner半圆法

1 引言

随着电子侦察能力的增强，常规体制的雷达面临着严重的生存威胁，雷达波形易于被敌方截获、干扰，从而使雷达的有效探测能力大打折扣，使雷达很难正确地发现并跟踪目标，并且易于被反辐射导弹(ARM)摧毁。为提升雷达的抗截获能力，各种新颖的低截获概率雷达波形被设计出来。然而这些波形的抗截获性能好坏，多依靠工程师的经验判断，往往缺乏理论依据。雷达信号的抗截获性能和信号的不确定性有着密切联系，有的学者提出用信息熵来评价雷达信号的不确定性，因此相应地提出了信号类型熵、密度熵、时频分布熵、安全信息因子等概念[1,2]。还有的学者提出将时间带宽积，峰均功率比，参数捷变特性等准则作为雷达信号的抗截获性能的评价准则[3]。一般意义上，白噪声具有最大的信息不确定度，因此具有最好的抗截获性能，如果一种雷达信号具有接近白噪声的信息不确定度，即可认为该信号具有较强的抗截获性能。另一方面，在信息论中，信息散度通常用来度量两个概率分布之间有多大的不同[4,5]。将白噪声信号和雷达信号分作两个不同的信号集合，可采用信息散度对两个集合的相似程度进行评价，通过选取当下常用的13类典型雷达信号波形作为测试对象，得出了在典型参数选取情况下不同雷达信号的抗截获性能差异程度。

2 算法原理

为了简化分析，对信号序列做标准化处理，首先对信号序列的方差和均值进行估计，采用极大似然估计方法。信号序列的估计均值和估计方差可以表示为

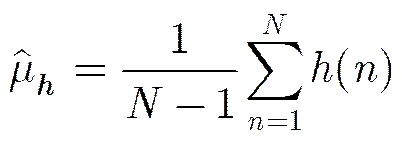
(3)

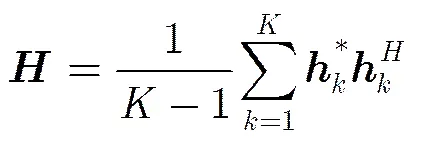
(6)

进而可得

(8)

(10)

本文利用雷达发射信号采样值构造信号Wigner矩阵，将其特征值的概率分布函数作为公式(1)中的；相应地，由噪声采样值构造噪声Wigner矩阵，再将其特征值的概率分布函数作为式(1)中的。

将式(11)展开为

可见，若已知分布函数，则能计算出它们的KL散度值。本文将式(12)作为白噪声信号集合和雷达信号集合之间的距离函数，即式(1)中的。

(14)

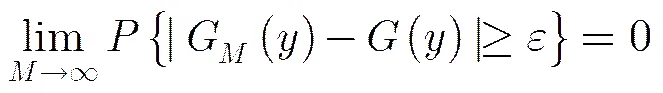
所以可以将式(13)表示为

将式(14)代入到式(16)可以得到：

其中，

将式(17)代到式(1)中可以得到

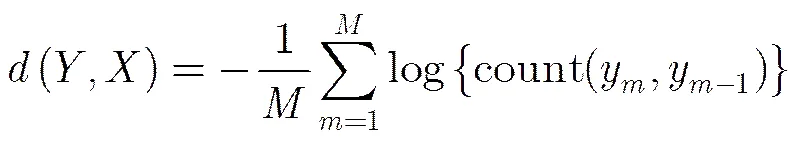
算法中作为参照标准的白噪声信号为理想白噪声信号，即信号的带宽无限，功率谱在整个频域范围内均匀分布，信号自相关函数为一个冲激函数。采用理想白噪声信号作为参照的主要原因是：理想白噪声信号的信号特性有利于式(12)的简化，有利于降低算法的复杂度，简化后的KLD的值仅与测试信号自身的特性有关，与白噪声信号的参数特性无关，所以在比对的过程中没有考虑噪声的带宽影响。

3 仿真验证

这里选用工程中常用的13类雷达信号波形进行抗截获性能分析，即：常规信号(NS)、线性调频信号(LFM)、多项式调频信号(PPS)、双线性调频信号(DLFM)、分段线性调频信号(MLFM)、非线性调频信号(NLFM)、二相编码信号(BPSK)、四相编码信号(QPSK)、多相编码信号(MPSK)、频移键控信号(FSK)、线性调频-二相编码复合调制信号(LFM/BPSK)、频移键控—相位编码复合调制信号(FSK/BPSK)和噪声调频信号[11,12]。并简要通过仿真验证了频率捷变和脉冲重复频率(PRF)对雷达信号抗截获性能的影响。3.1节分析了一定参数选取情况下前12类信号的抗截获性能，3.2节分析了相同带宽时不同信号的抗截获性能，3.3节分析了噪声调频雷达信号的抗截获性能，3.4节和3.5节分别分析了频率捷变和PRF对抗截获性能的影响。

3.1前12类信号的抗截获性能

仿真参数设置如下：

信号公共参数：总长度为2000采样点，采样频率为100 MHz。其他参数如下：

(1) NS：载频30 MHz；

(5)MLFM：信号分两段，载频均为10 MHz，调频系数均为Hz/s；

(6)NLFM：采用S型函数进行构造，载频为10 MHz，调制带宽为10 MHz；

(7)BPSK：采用的PN码为[1 1 1 1 1 0 0 1 1 0 1 0 1]，码元个数为13，码元宽度为154采样点，载频为30 MHz；

(8) QPSK：采用的PN码为[0 1 2 3 1 3 1 3 1 3 2 1 0]，码元个数为13，码元宽度为154采样点，载频为30 MHz；

(9)MPSK：采用16位Frank, P1, P2, P3和P4码，码元宽度为125采样点，载频为30 MHz；

(10)FSK：采用的调频序列为[15 20 5 10 30 25 10 15 25 30]MHz，每个频点持续时间为200采样点；

(11)LFM/BPSK：采用的PN码为[1 1 1 1 1 0 0 1 1 0 1 0 1]，码元个数为13，码元宽度为154采样点，载频为30MHz，调频系数为Hz/s；

(12)FSK/BPSK：调频序列为[20 10 30 20] MHz，每跳中的PN码为[0 1 1 0]，码元宽度为125采样点；

仿真结果如图1所示。

从仿真结果可以看出，在上述参数选择条件下，线性调频信号有着较好的抗截获性能，而常规信号抗截获性能最差。多相编码信号抗截获性能相近。采用频率调制类的信号抗截获性能比采用相位调制类的信号抗截获性能更好。

3.2相同带宽情况下信号的抗截获性能

信号的发射带宽对信号的抗截获性能有着较大的影响，相同的发射信号类型在不同的带宽的情况下，抗截获性能往往不同，下面着重分析在相同带宽情况下各个信号的抗截获性能。信号的带宽设置为0.4 MHz，仿真结果如图2所示。

由于常规雷达信号在脉冲内部为点频信号，所以图2不包含。从图2的仿真结果可以看出，在相同带宽的情况下，调频类雷达信号有着几乎相同的抗截获性能，调相类雷达信号的抗截获性能优于调频类信号，复合调制信号则有着最优的抗截获性能。

3.3噪声调频信号的抗截获性能

噪声调频雷达的发射信号为[13,14]：

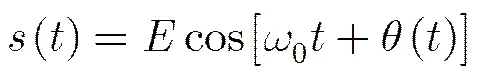
仿真参数[15,16]：

(1)信号总长度为1200采样点，采样频率为2 GHz，载频为100 MHz，带宽为100 MHz。

(2)信号总长度为1200采样点，采样频率为2 GHz，载频为100 MHz，带宽为400 MHz。

分别对上述两种参数的噪声调频信号进行蒙特卡洛仿真，仿真次数为1000次。仿真参数(1)和(2)情况下，计算所得KLD值分别为0.9125和0.7537。

仿真结果表明带宽为400 MHz的噪声调频信号抗截获性能要优于带宽为100 MHz的信号。

3.4载频捷变对信号抗截获性能的影响

雷达载频捷变是一种常见的脉间抗截获技术，有脉间捷变、脉组捷变等。捷变方式可以按一定的规律变化，也可以随机跃变，还可以有针对性地在干扰频带的空隙或弱区进行自适应频率捷变。这里采用调频连续波雷达信号作为测试信号，时域表达式为

仿真结果表明载频捷变比载频恒定有着更好的抗截获性能，而且载频变化的越频繁、越剧烈，抗截获的性能越好。

3.5脉冲重复频率对信号抗截获性能的影响

脉冲重复间隔(Pulse Repetition Interval, PRI)即雷达相邻发射脉冲前沿的时间间隔，其倒数被称为脉间重复频率(PRF)，简称重频。这里着重分析重频参差对信号抗截获性能的影响，重频参差雷达采用两个或两个以上的脉冲重复频率，通过顺序、循环利用脉冲重复序列集合中的PRI值产生脉冲序列。

重频参差雷达发射信号时域表达式为

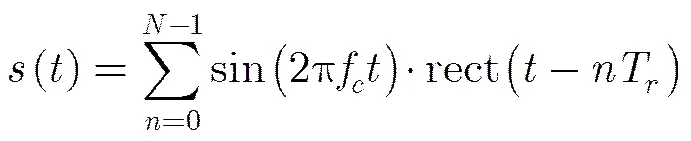
仿真参数：信号总长度为8000采样点，采样率为100 MHz，共10个脉冲，脉冲宽度均为100点，载频均为5 MHz。脉冲重复频率设置为：(1)PRF固定，为800点；(2) PRF三重参差，分别为：200点、500点、800点。

PRF参数(1)和(2)情况下，计算所得KLD值分别为：0.8672和0.7578。

比较两种PRF参数选取情况下的仿真结果可以发现，采用重频参差技术可以有效改善雷达信号的抗截获性能。

4 结束语

本文针对雷达信号波形抗截获性能评价问题，以高斯白噪声信号为基准，将不同雷达信号波形与高斯白噪声信号的信息散度作为抗截获性能指标，为雷达信号波形抗截获性能评价建立了一种可量化的度量方法。理论分析和仿真结果表明，信息散度越小，雷达信号功率谱分布越接近于白噪声的功率谱分布，信号能量在频带范围内的分布也就越均匀，在同等发射能量和带宽情况下，该信号波形与白噪声的相似性越大，其抗截获性能也就越好。论文最后应用MATLAB仿真，针对13类常用雷达信号波形，验证了所提算法的有效性，为工程中设计、评价雷达信号的抗截获性能提供了一定参考。

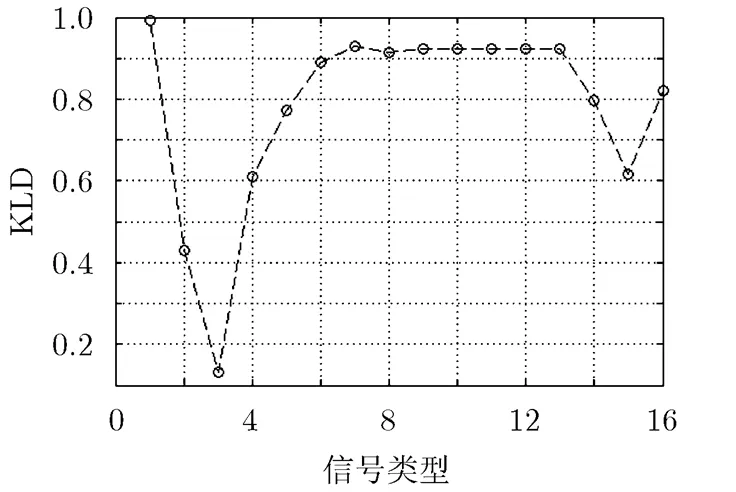
图1 前12类雷达信号的抗截获性能

[1] 陈利虎. 跳频信号的侦察技术研究[D]. [博士论文], 国防科学技术大学, 2009.

[2] WANG F, SELLATHURAIM, LIU W,. Security information factor based airborne radar RF stealth[J]., 2015, 26(2): 258-266. doi: 10.1109/JSEE.2015.00031.

[3] FANCEYC and ALABASTERC M. The metrication of low probability of intercept waveforms[C]. IEEE International Conference on Waveform Diversity and Design, Falls Niagara, Canada, 2010: 58-62. doi: 10.1109/WDD.2010.5592358.

[4] TUMMINELLO M, LILLO F, and MANTEGNA R N. Shrinkage and spectral filtering of correlation matrices: a comparison via the Kullback–Leibler distance[J]., 2007, 38: 4079-4088.

[5] CONTERAS-REYES J E. Asymptotic form of the Kullback-Leibler divergence for multivariate asymmetric heavy-tailed distributions[J].:&, 2014, 395(4): 200-208.

[6] ERD˝OS L, KNOWLES A, YAU H T,. The local semicircle law for a general class of random matrices[J]., 2013, 18(12): 2140-2154.doi: 10.1214/EJP.v18-2473.

[7] BAI Z D, MIAO B, and TSAY J. Convergence rates of the spectral distributions of large Wigner Matrices[J]., 2002, 1(1): 65-90.

[8] GÓTZE F, NAUMOV A, TIKHOMIROV A N,. Local semicircle law under weak moment conditions[J]., 2016, 93(3): 248-250.doi: 10.1134/S10645624 16030029.

[9] BIROLI G, BOUCHAUD J P, and POTTERS M. The student ensemble of correlation matrices: eigenvalue spectrum and Kullback–Leibler entropy[J]., 2007, 38: 4009-4026.

[10] BU Y, ZOU S, LIANG Y,. Estimation of KL divergence between large-alphabet distributions[C]. IEEE International Symposium on Information Theory. Barcelona, Spain, 2016: 1118-1122.

[11] JIANG L, LI L, and ZHAO G Q. Polyphase coded low probability of intercept signals detection and estimation using time–frequency rate distribution[J]., 2016, 10(1): 46-54. doi: 10.1049/iet-spr.2014.0020

[12] 李秀友, 董云龙, 张林, 等. 一种新的低旁瓣LFM噪声雷达波形设计方法[J]. 电子与信息学报, 2016, 38(6): 1452-1459. doi: 10.11999/JEIT151070.

LI Xiuyou, DONG Yunlong, ZHANG Lin,. A new design method of low side lobe level LFM noise radar waveform[J].&, 2016, 38(6): 1452-1459. doi: 10.11999/JEIT151070.

[13] 倪浩杰. 基于FPGA的噪声调频雷达信号处理系统的设计与实现[D]. [硕士论文], 南京理工大学, 2008.

[14] 王钊, 顾红, 苏卫民, 等. 基于共轭噪声组的宽带噪声雷达机动目标参数估计[J].电子与信息学报, 2015, 37(5): 1071-1077. doi: 10.11999/JEIT140737.

WANG Zhao, GU Hong, SU Weimin,. Parameter estimation of maneuvering targets in wideband noise radar based on conjugate noise group[J].&, 2015, 37(5): 1071-1077. doi: 0.11999/JEIT140737.

[15] 郑慧芳, 邓云凯. 随机噪声调频信号带宽分析[J]. 科学技术与工程,2009, 9(15): 4351-4357. doi: 10.3969/j.issn.1671-1815. 2009.15.018.

ZHENG Huifang and DENG Yunkai. Analysis of random noise frequency modulation signal's bandwidth[J].,2009, 9(15): 4351-4357. doi: 10.3969/j.issn.1671-1815.2009.15.018.

[16] HEUSCHEL E R. Time-frequency, bi-frequency detection analysis of noise technology radar[D]. [Ph.D. dissertation], Monterey California Naval Postgraduate School, 2006.

Anti-interception Performance Evaluation of Radar Signal Waveform Based on KL Divergence

WANG Xudong LU Wei YAN He

(,,211106,)

This paper presents a new method for evaluating the anti-interception performance of thirteen kinds of radar signals, which can be used to guide radar waveform designing. The method assumes that white noise signal has the best anti-interception performance, by comparing different radar signals with it, the similarity degree of radar signal and white noise signal can be obtained. First, the characteristics distribution function of white noise and radar signal distribution function are introduced using Wigner semicircle law. Second, KL divergence is used to represent the similarity between radar signal and white noise. Small value of KL divergence means better anti interception performance, and vice versa. Theoretical derivation and simulation results show that this method can evaluate the anti interception performance of different radar signals effectively.

Radar signal waveform; Anti-interception performance; Evaluation criterion; KL divergence; Wigner semicircle law

TN974

A

1009-5896(2017)08-1894-05

10.11999/JEIT161124

2016-10-21；

改回日期：2017-03-17；

2017-04-25

陆威 834185768@qq.com

国家自然科学基金(61201208)，中国博士后科学基金(2014M561643)，中央高校基本科研业务费专项资金(NJ20150018)

The National Natural Science Foundation of China (61201208), China Postdoctoral Science Foundation (2014M561643), The Fundamental Research Funds for the Central Universities (NJ20150018)

王旭东： 男，1978年生，博士，副教授，研究方向为信号检测、参数估计、FPGA设计应用.

陆 威： 男，1992年生，硕士生，研究方向为雷达信号检测与估计.

闫 贺： 男，1985年生，博士，讲师，研究方向为广域运动目标监视.