真空法动态制冰的非等温结晶动力学
2017-10-14刘曦庄焜煜黄成李学来
刘曦,庄焜煜,黄成,李学来
真空法动态制冰的非等温结晶动力学
刘曦,庄焜煜,黄成,李学来
(福州大学石油化工学院,福建福州350116)
以氯化钠水溶液为制冰溶液,采用真空法制备得到冰浆。从理论上论证非等温结晶动力学模型Jeziorny法和Mo法用于描述冰浆结晶行为的可行性。通过实验测定不同结晶时间下的冰浆含冰率,并建立了冰浆生成过程的非等温动力学方程。研究结果表明:Jeziorny法和Mo法可很好地描述冰浆的非等温结晶过程;Jeziorny模型指数的值在0.473~0.525间,表明不同实验条件下的结晶机理基本一致,冰晶呈片状增厚生长;Jeziorny模型中的结晶动力学参数c、0.25和Mo模型中的冷却速率函数()的变化规律均表明高冷却速率可促进冰浆的形成,同时氯化钠的添加会在一定程度上抑制冰晶生长。
冰浆;结晶;动力学;真空制冰;动力学模型
引 言
冰浆作为一种新型蓄冷介质,具有蓄冷密度高、释冷速度快、流动性和换热性良好等优点,在能源短缺且电力峰谷供需不平衡的当今,发展以冰浆为载冷介质的蓄冷技术具有十分重要的意义[1-4]。真空法作为一种典型的动态冰浆制备技术,因具有热效率高、操作方便、过程稳定等特点而备受关注。国内外的许多科研机构及公司都在此领域展开了研究,并取得了一定的成果。
Shin等[5-6]测定了真空环境下不同颗粒的水滴在下落过程中温度随时间的变化情况,同时基于扩散蒸发模型分析了液滴在真空室中闪蒸过程的热、质交换,建立了冰晶形成过程的数学模型。Isao等[7]研究了水滴的真空蒸发特性与水滴初温、直径和真空度的关系,并对过冷现象进行了探讨。刘伟民等[8-9]观察了液滴在真空环境中发生闪蒸过程所经历的6种形态,解释了液滴内不同位置点温度的变化机理。章学来等[10-14]分析了不同环境温度、环境压力、供水水温、水质、粒径及水滴下落初速度等情况下水滴温度随时间的变化特性及这些因素对含冰率的影响规律,在此基础上探讨了乙醇水溶液、液态水膜等介质的真空闪蒸过程。同时,还设计了一种带吸附功能的真空制冰装置,发现吸附模块可有效降低闪蒸室内的压力,促进冰浆形成。赵红霞等[15]基于㶲分析法,计算了真空闪蒸冰浆制备系统的㶲损失和㶲效率。Lugo等[16]对氨水溶液和乙醇水溶液处于汽-液-固三相共存状态下的压力和温度进行了测定,并用热力学模型验证了实验数据,结果表明该实验数据可用于真空制冰系统的设计。Asaoka等[17-18]测定了乙醇水溶液在冻结温度和20℃下的汽液平衡数据,在此基础上观测乙醇水溶液的结晶过程,并测定结晶过程中制冰溶液浓度和蒸汽浓度之间的关系,最终测算了系统的制冷能效比。产品开发方面,以色列IDE技术有限公司已成功开发了VIM系列和ECO-VIM系列真空制冰机,并在矿井降温、人工造雪等领域投入使用[19]。
虽然近20年来,各国学者已从热质交换、热力学等角度对真空法冰浆制备展开了大量的研究,然而真空制备技术的实际应用仍相对较少,除了以色列IDE技术有限公司开发的真空制冰机外,尚未发现其他公司利用真空法生产冰浆。制约真空法制冰技术发展的主要原因在于对冰浆制备过程的结晶动力学机理尚未有准确可靠的认识。结晶动力学可揭示冰晶的成核机制及含冰率与结晶时间的关系,是真空制冰机的设计与过程优化、控制的基础,然而目前真空环境下冰晶生成过程的动力学研究几乎未见报道。
为此,本文基于非等温结晶动力学理论分析冰浆生成过程的结晶行为。首先,从理论上论证非等温结晶动力学模型(Jeziorny方程和Mo方程)应用于描述冰浆结晶动力学的可行性,在此基础上,通过实测数据,获得相应的动力学参数,掌握成核机理,得到总结晶速率方程,并探明添加剂浓度、操作参数等对结晶过程的影响规律。研究成果可为工业应用中冰浆结晶速率的在线预测提供参考。
1 理论分析
真空法冰浆制备过程中,既有相变过程的传热传质,也有同一相间的传热传质,过程涉及相变热力学、流体力学、传热传质学、真空技术等。通常真空制冰系统包括真空泵、冷凝器和真空罐,若从传热传质角度分析冰浆生成速率,需对整个系统进行动力学分析,十分复杂,且系统热损失、蒸发过程的蒸发阻力、凝结过程的凝结系数、真空罐的漏气量、冷凝室的漏气量等均难以估算[20],故通过传热传质理论分析结晶动力学特性将存在较大误差。
从热量守恒角度考虑,冰的生成是因为部分水的蒸发需要吸热,因此,冰浆的含冰率主要取决于水的蒸发速率和制冰时间(即结晶时间),故有
=(W,) (1)
式中,W为水的蒸发速率,Pa·m3·s-1;为结晶时间,s。
同等条件下,水的蒸发速率越大,则含冰率越高。水的蒸发速率可表示为

式中,W为溶液的饱和温度,K;W为溶液蒸发面积,m2;W为溶液的饱和蒸气压,Pa;W1为真空室内水蒸气的压力,Pa;为Boltzmann常数;0为液体分子质量,kg;为液体表面蒸发系数。
可将、0和视为常数,真空室内水蒸气的压力主要取决于蒸汽被抽出和被冷凝的速率,即真空泵的抽速和冷凝器的冷凝能力。综合以上分析,可知冰浆含冰率可表征为以下一系列参数的函数
=(W,W,W,p,L,) (3)
式中,p为真空泵的抽速,m3·s-1;L为冷凝器的冷凝能力,Pa·m3·s-1。
分析式(3),可发现:溶液的饱和温度和饱和蒸气压即为结晶时的三相点温度和压力,它们是一一对应的,可用结晶过程中的冷却速率和结晶时间来表征;蒸发面积W、真空泵的抽速p、冷凝器的冷凝能力L3个参数的变化,都会引起冷却速率的改变。例如:蒸发面积及真空泵抽速相同时,若冷凝器的冷凝能力越大,则系统降温、降压越快,因此可统一用冷却速率和冰晶生成时间来概括上述一系列参数对冰浆生成率的影响,式(3)简化为
=(,) (4)
若能获得与、间的关系,即可通过冰晶生成时间和冷却速率来实时判断冰浆的含冰率,这对工业生产具有十分重要的意义。冰晶生成过程实际上是一典型的液-固相变过程,在材料学的研究中,常用相变动力学速率模型来描述系统在相变过程中新相宏观转化率与相变时间的关系,包括等温结晶过程的Avrami方程及非等温结晶过程的Jeziorny方程、Ozawa方程和Mo方程[21-24]。
Avrami方程的具体形式为

式中,为结晶速率常数,为Avrami指数。
Avrami方程的推导是基于概率统计理论的,因此,只要过程涉及成核和生长,理论上便可以用Avrami模型来描述。Avrami模型最初多被用于高分子结晶过程的分析[25-26],目前,已有较多关于Avrami模型用于其他研究领域的报道,如陶瓷、玻璃、小分子金属等物质的等温结晶研究[27-32]。
真空法冰浆制备过程中,冰晶的生成同样是液-固相变过程,也必须经历成核与生长两个步骤,若采用纯水制冰,则冰浆生成过程可视为等温过程,其含冰率与时间的关系理论上可用Avrami方程描述。若采用水溶液制冰,则随着水蒸气的蒸发及冰晶的生成,溶液浓度越来越高,所对应的相变温度和压力不断减小,即冰浆生成过程为典型的非等温过程,其生成速率理论上可用基于Avrami方程推导得到的非等温结晶过程动力学方程:Jeziorny方程、Ozawa方程和Mo方程来描述。
Jeziorny方程可由Avrami方程转换而得,对Avrami方程两边取对数
ln[-ln(1-())]=ln+ln(6)
考虑到冷却速率对结晶的影响,Jeziorny方程对结晶速率常数进行适当的修正。假设冷却速率不变或近似不变,则非等温结晶动力学特性参数c可以通过式(7)修正
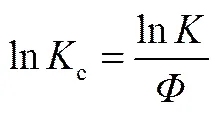
式中,c为非等温结晶速率常数。
Ozawa方程假设非等温结晶过程是由无限小的等温结晶过程组成,故得到
1-()=exp[-()/Φ] (8)
式中,()为温度时的相对结晶度;为Ozawa指数,其物理意义与Avrami指数相同;()为温度的函数。
对式(8)两边取对数得
ln[-ln(1-())]=ln()-ln(9)
在非等温条件下,对于同一体系,在冷却速率为时,某时刻和温度的关系如下

式中,0为=0时刻的温度。
对于一定的研究体系,在某时刻,必然存在与时刻相对应的温度时的相对结晶度(),故基于式(10),关联式(6)与式(9)的左边项
ln[-ln(1-())]=ln[-ln(1-())] (11)
关联式(6)与式(9)的右边项
ln+ln=ln()-ln(12)
将式(12)整理变形,得到

令()=[()/]1/m,=/,可得到Mo方程
ln=ln()-ln(14)
式中,()为冷却速率函数,其物理意义为对某一体系,在单位时间内达到某一相对结晶度时所需的冷却速率,()可作为表征结晶快慢的参数。
冰晶生成过程中溶液温度不断下降,Jeziorny模型和Mo模型中的冷却速率通常使用降温或降压速率来表示,因实验过程中,温度的降幅较小,故采用单位时间内的压力降幅来表征冷却速率

式中,为冷却速率,Pa·min-1;Δ为初始冰晶生成时的压力与实验结束时的系统压力之差,Pa;为初始生成冰晶至实验结束所经历的时间,即结晶时间,s。
2 实验装置与方法
真空制冰实验系统如图1所示,该系统由冰浆生成罐、旋片式真空泵、绝压变送器、压力采集器、热电偶、温度采集器、冷凝器、磁力搅拌器及计算机组成。真空泵抽速为2 L·s-1;绝压变送器型号为WH3051,量程为0~9 kPa,精度为±0.075%FS;T形热电偶测量精度为±0.5%。当真空制冰系统产生冰晶时,其溶液温度会产生阶跃,对应的水蒸气压力也将改变,因此,可通过监测压力数据和温度数据的变化来判断冰晶是否生成。当结晶时间达到预设的结晶时间时(45、70、90、130、180、310、410、510、650 s),关闭真空泵,并测量冰浆的含冰率。
冰浆的含冰率采用量热法测定,将制备得到的冰浆样品与20 g、温度为40℃的热水混合,测定混合前后的质量、温度等参数,并基于热量守恒计算获得含冰率

(17)
式中,i为冰浆中冰的质量,g;0为冰浆的温度,℃;1为冰浆与热水混合后的溶液温度,℃;1为水的比热容,J·g-1·K-1;2为溶液的比热容,J·g-1·K-1;1为冰浆溶液的总质量,g;为固态冰的融解潜热,J·g-1;i为冰的密度,g·cm-3;s为溶液的密度,g·cm-3。
为验证量热法及测温装置的可靠性,用天平分别称取质量为1、2、3、4和5 g的固态碎冰,并加入至15 g、温度为0℃的液态水中,配制得到理论含冰率分别为6.3%、11.8%、16.7%、21.1%和25.0%的冰浆,随后立即将冰浆与20 g、温度为40℃的热水混合,测定混合后的溶液温度并计算得到含冰率,分别为6.1%、11.6%、16.8%、21.2%和24.5%,对比以上数据,可知实验值与理论值间的相对误差分别为−3.2%、−1.7%、0.6%、1.0%和−2.0%,误差值较小,因此认为采用量热法测定得到的冰浆含冰率真实可靠。
3 结果与讨论
3.1 基于Jeziorny方程的非等温结晶行为
分别测定20 ml、浓度(质量分数)分别为0.5%、1%、2%和3%的氯化钠水溶液在不同冷却速率下的含冰率,得到不同冷却速率下含冰率与结晶时间的关系,如图2所示。不同冷却速率下氯化钠水溶液所生成冰浆的含冰率随时间变化的趋势基本一致:结晶初始阶段,曲线较陡,意味着冰浆生成速率较快,随着时间的延续,曲线变缓,即冰浆生成速率逐渐减慢;相同的含冰率下,冷却速率越大,完成结晶所需的时间越短,同时当结晶时间相同时,冷却速率越大,生成的冰浆含冰率越高,即结晶速率越快。分析其原因,主要是因为较高的冷却速率必然对应着较大的过冷度,过冷度是冰晶成核与生长的推动力,过冷度越大,成核和生长速率也越大,因此在相同时间内生成的冰浆也必然越多。
图3为不同冷却速率下的ln[−ln(1−)]和ln关系图。从图中可看出,ln[−ln(1−)]与ln间呈现出良好的线性关系,拟合度较好,这说明Jeziorny法适用于描述真空冰浆制备过程中氯化钠水溶液的非等温结晶特性。
考察氯化钠初始浓度对冰浆生成速率的影响,得到相同冷却速率下含冰率与结晶时间的变化关系,如图4所示。由图可知:相同含冰率下,溶液初始浓度越大,结晶完成的时间则越长,这说明了氯化钠对冰晶的生成起到了一定程度的抑制作用。氯化钠水溶液中,存在着O—H…Cl型氢键,虽然这种氢键的键能较小,但也可在一定程度上影响到水分子与水分子间自身氢键的形成,由此抑制了冰晶的生成,因此氯化钠浓度越高,结晶所需时间越长。
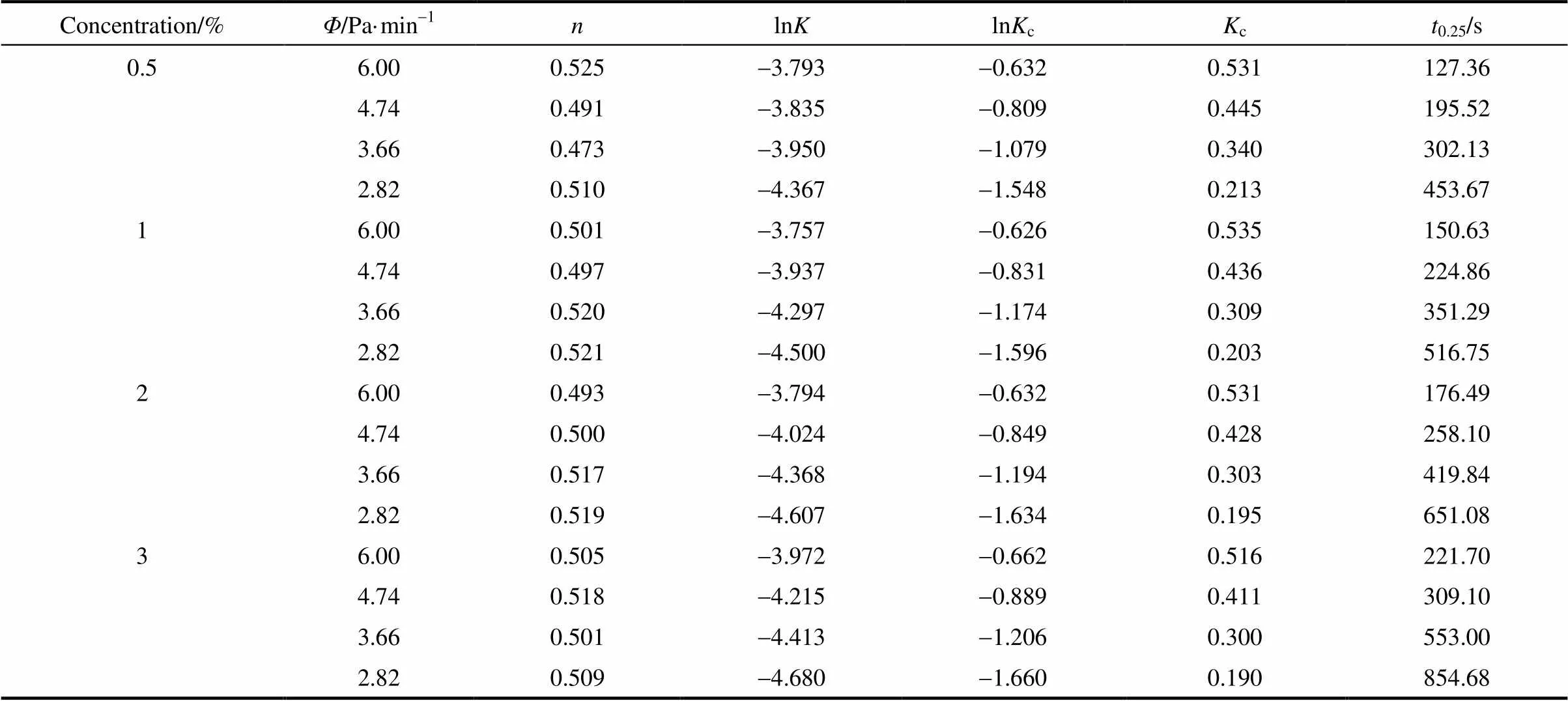
表1 Jeziorny法非等温结晶动力学参数
图5为氯化钠水溶液在不同初始浓度下的ln[−ln(1−)]和ln的关系图。从图中可以看出,ln[−ln(1−)]与ln呈现良好的线性关系,拟合度较好,故不同初始浓度下氯化钠水溶液的非等温制备冰浆过程可采用Jeziorny法描述。
根据Jeziorny法可以得到氯化钠水溶液真空制冰过程的结晶动力学参数,列于表1。表中0.25表示当含冰率达到25%时所需的结晶时间,其计算式如下
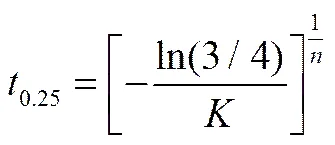
材料学中一般采用0.5这一指标来表示结晶的快慢,考虑到实际冰浆应用中,为了提高冰浆的流动性能,降低流体黏度,一般采用含冰率为20%~30%的冰浆,故本文中以当含冰率达到25%时所需的结晶时间0.25来表征结晶的快慢。
从表1中可看出:不同实验条件下,指数的值均小于1,位于0.473~0.525间,且都为非整数,这说明在实验设定的溶液浓度和冷却速率范围内,氯化钠水溶液中冰晶的成核行为基本一致。模型指数通常可揭示相变机制和生长形态,具体如表2所示[33]。本文得到的值约为0.5,表明冰晶呈片状增厚生长,并且生长过程受扩散控制。采用显微装置对冰晶颗粒进行观测,可发现冰晶大多呈近似圆形或椭圆形,是一种二维形态[34]。值不为整数,有可能是由以下原因造成:①冰晶生长过程中因为搅拌、团聚、熟化等因素产生了新的形状不规则的新冰晶;② 在同一结晶过程中可能同时存在不同的结晶机制。

表2 各种转变机制下的n值
以0.5%氯化钠水溶液为例,分析c与0.25随冷却速率的变化关系,如图6所示。可发现对同一初始浓度的氯化钠水溶液,制冰过程中,若冷却速率越大,则对应的结晶速率常数c也越大,而结晶时间0.25则越小。当冷却速率相同时(以冷却速率等于6 Pa·min-1为例),如图7所示,结晶时间0.25的值随氯化钠浓度的增大而显著增大,这同样说明了增大氯化钠的添加会抑制真空制冰过程中冰晶的形成,导致结晶时间变长,而结晶速率常数c的值位于0.516~0.535之间,基本无变化。
3.2 基于Mo法的总结晶速率
采用Mo方程分析冰浆生成过程冷却速率和结晶时间两者之间的关系,根据式(14),以ln对ln作图,如图8所示。对所得曲线进行拟合得到氯化钠水溶液非等温结晶动力学参数列于表3。从图8中可看出,氯化钠水溶液的ln-ln关系曲线均具有很好的线性关系,因此,可用Mo法分析氯化钠水溶液真空环境下的冰浆生成过程。从表3可以看出,对于同一初始浓度的氯化钠水溶液,随着相对结晶度的增大,()的值不断增大,这表明在某一温度时刻,单位结晶时间内体系达到某一结晶度所需要的冷却速率增大,亦即冷却速率越大,结晶速率越大。

表3 Mo法非等温结晶动力学参数
4 结 论
(1)提出了采用冷却速率和冰晶生成时间这两个参数来概括众多因素对冰浆总结晶速率的影响,即认为冰浆总结晶速率取决于冷却速率和冰晶生成时间,并基于非等温结晶动力学模型Jeziorny方程和Mo方程,成功描述了冰浆制备过程中含冰率随冰晶生成时间、冷却速率的变化关系,为工业应用中冰浆含冰率的在线预测提供了参考。
(2)基于实验得到了Jeziorny方程的结晶速率常数c和结晶时间0.25,根据这两个参数在不同实验条件下的变化趋势,可知:提高制冰过程的冷却速率可加速冰浆的生成;氯化钠在一定程度上会阻碍冰晶的形成,具体体现在当添加浓度增大时,结晶速率常数c减小同时结晶时间0.25增大。
(3)基于实验得到了Mo方程的冷却速率函数(),这一参数同样可反映冰浆生成速率的快慢:当制冰溶液初始浓度增大时,()值随之增大,表明此时若要制得同样含冰率的冰浆,浓度越高的溶液所需的冷却速率越大;当制冰溶液初始浓度相同时,()值随含冰率的增大而增大,表明在单位时间内若需达到较高的含冰率,就必须加快冷却速率。
符 号 说 明

AW ——溶液的蒸发面积,m2 C(T) ——温度T时的相对结晶度 c1——水的比热容,J·g-1·K-1 c2——溶液的比热容,J·g-1·K-1 F(T) ——冷却速率函数 K ——结晶速率常数 Kc——非等温结晶速率常数 k ——Boltzmann常数 L——固态冰的融解潜热,J·g-1 m ——Ozawa指数 mi——冰浆中冰的质量,g m0 ——液体分子质量,g m1——冰浆溶液的总质量,g n ——Avrami指数 pW ——溶液的饱和蒸气压,Pa pW1 ——真空室内水蒸气的压力,Pa Δp ——系统压力差,Pa qL ——冷凝器的冷凝能力,Pa·m3·s-1 qW ——水的蒸发速率,Pa·m3·s-1 Sp ——真空泵的抽速,m3·s-1 TW ——溶液的饱和温度,K t ——结晶时间,s t0——冰浆的温度,℃ t1——冰浆与热水混合后的溶液温度,℃ α——液体表面蒸发系数 ρi——冰的密度,g·cm-3 ρs——溶液的密度,g·cm-3 Φ ——冷却速率,Pa·min-1
References
[1] FANG G Y, TANG F, CAO L. Dynamic characteristics of cool thermal energy storage systems—a review[J]. International Journal of Green Energy, 2016, 13(1): 1-13.
[2] LI G, HWANG Y H, RADERMACHER R. Review of cold storage materials for air conditioning application[J]. International Journal of Refrigeration, 2012, 35(8): 2053-2077.
[3] YAU Y H, RISMANCHI B. A review on cool thermal storage technologies and operating strategies[J]. Renewable and Sustainable Energy Reviews, 2012, 16(1): 787-797.
[4] KAUFFELD M, WANG M J, GOLDSTEIN V,. Ice slurry applications[J]. International Journal of Refrigeration, 2010, 33(8): 1491-1505.
[5] KIM B S, SHIN H T, LEE Y P,. Study on ice slurry production by water spray[J]. International Journal of Refrigeration, 2001, 24(2): 176-184.
[6] SHIN H T, LEE Y P, JURNG J. Spherical-shaped ice particle production by spraying water in a vacuum chamber[J]. Applied Thermal Engineering, 2000, 20(5): 439-454.
[7] ISAO S, KAZUYOSHI F, YU H. Freezing of water droplet due to evaporation-heat transfer dominating the evaporation-freezing phenomena and the effect of boiling on freezing characteristics[J]. International Journal of Refrigeration, 2002, 25(2): 226-234.
[8] 刘伟民, 毕勤成, 刘璐, 等. 低压闪蒸液滴形态和温度变化的研究[J]. 工程热物理学报, 2007, 28(6): 957-960. LIU W M, BI Q C, LIU L,. Study on the shape and temperature variations within droplet in low pressure enviroment[J]. Journal of Engineering Thermophysics, 2007, 28(6): 957-690.
[9] 刘伟民, 毕勤成, 杨东, 等. 低压闪蒸液滴温度与相变过程的研究[J]. 应用基础与工程科学学报, 2005, 13(4): 381-387.LIU W M, BI Q C, YANG D,. Study on temperature and phase change of water droplet in the process of flash under low pressure[J]. Journal of Basic Science and Engineering, 2005, 13(4): 381-387.
[10] 章学来, 李晓菲, 高文忠, 等. 真空制冰过程中水滴动态特性[J]. 化工学报, 2012, 63(5): 1373-1378. ZHANG X L, LI X F, GAO W Z,. Analysis on droplet temperature in binary ice preparation by vacuum method[J]. CIESC Journal, 2012, 63(5): 1373-1378.
[11] 纪珺, 章学来, 刘小微, 等. 水膜闪蒸真空制冰的换热特性[J]. 化工学报, 2013, 64(4): 1236-1241. JI J, ZHANG X L, LIU X W,. Heat transfer characteristics of water film flash evaporation in vacuum ice making[J]. CIESC Journal, 2013, 64(4): 1236-1241.
[12] 章学来, 赵群志, 孟祥来, 等. 吸附作用下真空制冰特性的实验分析[J]. 化工学报, 2014, 65(10): 4131-4137. ZHANG X L, ZHAO Q Z, MENG X L,. Experimental analysis of ice-making characteristics with adsorption in vacuum environment[J]. CIESC Journal, 2014, 65(10): 4131-4137.
[13] 黄亮, 章学来. 乙醇溶液液滴降压闪蒸特性[J]. 化工学报, 2016, 67(9): 3762-3767. HUANG L, ZHANG X L. Flash evaporation characteristics of ethanol solution droplets under depressurization[J]. CIESC Journal, 2016, 67(9): 3762-3767.
[14] ZHANG X L, HAN Z, LI Z W. Analysis on IPF influencing factors for vacuum binary ice making method[J]. International Journal of Thermal Sciences, 2013, 67(5): 210-216.
[15] 赵红霞, 孙冰洁, 冀翠莲, 等. 真空闪蒸制取冰浆系统㶲分析[J]. 化工学报, 2013, 64(8): 2724-2729. ZHAO H X, SUN B J, JI C L,. Exergy analysis on ice slurry production system by water spray evaporation in vacuum environment[J]. CIESC Journal, 2013, 64(8): 2724-2729.
[16] LUGO R, FOURNAISON L, GUILPART J. Ice-liquid-vapor equilibria of ammonia and ethanol aqueous solutions applied to the production of ice-slurries prediction and experimental results[J]. Chemical Engineering and Processing, 2006, 45(1): 66-72.
[17] ASAOKA T, SAITO A, OKAWA S,. Vacuum freezing type ice slurry production using ethanol solution(Ⅰ): Measurement of vapor-liquid equilibrium data of ethanol solution at 20℃and at the freezing temperture[J]. International Journal of Refrigeration, 2009, 32(3): 387-393.
[18] ASAOKA T, SAITO A, OKAWA S,. Vacuum freezing type ice slurry production using ethanol solution(Ⅱ): Investigation on evaporation characteristics of ice slurry in ice production[J]. International Journal of Refrigeration, 2009, 32(3): 394-401.
[19] 吴继忠, 刘祥来, 姚向东, 等. 孔庄煤矿集中降温方案的选择与优化[J]. 中国工程科学, 2011, 13(11): 59-67. WU J Z, LIU X L, YAO X D,. Optimization of centralized cooling schemes in Kongzhuang coal mine[J]. Engineering Sciences, 2011, 13(11): 59-67.
[20] 张世伟, 张志军, 鄂东梅, 等. 液体真空蒸发冻结过程的动力学研究[J]. 真空科学与技术学报, 2009, 29(6): 619-623. ZHANG S W, ZHANG Z J, E D M,. Thermal dynamical study of vacuum freezing of liquids[J]. Chinese Journal of Vacuum Science and Technology, 2009, 29(6): 619-623.
[21] AVRAMI M. Kinetics of phase change(Ⅰ): General theory[J]. Journal of Chemical Physics, 1939, 7(12): 1103-1112.
[22] AVRAMI M. Kinetics of phase change(Ⅱ): Transformation time relations for random distribution of nuclei[J]. Journal of Chemical Physics, 1940, 8(2): 212-224.
[23] AVRAMI M. Granulation, phase change, and microstructure kinetics of phase change(Ⅲ)[J]. Journal of Chemical Physics, 1941, 9(2): 177-184.
[24] 莫志深. 一种研究聚合物非等温结晶动力学的方法[J]. 高分子学报, 2008, 1(7): 656-661. MO Z S. A method for the non-isothermal crystallization kinetics of polymers[J]. Acta Polymerica Sinica, 2008, 1(7): 656-661.
[25] ZHANG T Z, LI T, NIES E,. Isothermal crystallization study on aqueous solution of poly (vinyl methyl ether) by DSC method[J]. Polymer, 2009, 50(5): 1206-1213.
[26] 梁明霞, 张晓红, 宋志海, 等. 复合成核剂对聚丙烯结晶行为的影响[J]. 高分子学报, 2008, 1(10): 985-992. LIANG M X, ZHANG X H, SONG Z H,. The effect of compound nucleating agent on the crystallization behavior of polypropylene[J]. Acta Polymerica Sinica, 2008, 1(10): 985-992.
[27] USAMI N, JUNG M, SUEMASU T. On the growth mechanism of polycrystalline silicon thin film by Al-induced layer exchange process[J]. Journal of Crystal Growth, 2013, 362(1): 16-19.
[28] VAISH R, VARMA K B R. Glass transition and crystallization kinetics of CsLiB6O10glasses by differential scanning calorimetry[J]. Journal of Crystal Growth, 2007, 307(2): 477-482.
[29] KANG M, KANG S. Influence of Al2O3additions on the crystallization mechanism and properties of diopside/anorthite hybrid glass-ceramics for LED packaging materials[J]. Journal of Crystal Growth, 2011, 326(1): 124-127.
[30] ZHAO D H, ZHANG X H, XIA F,. Nonisothermal study on crystallization kinetics of GeSe2-As2Se3-CdSe chalcogenide glasses by differential scanning calorimeter[J]. Journal of Crystal Growth, 2005, 285(1/2): 228-235.
[31] KIMA W K, PAYZANTB E A, KIMA S,. Reaction kinetics of CuGaSe2formation from a GaSe/CuSe bilayer precursor film[J]. Journal of Crystal Growth, 2008, 310(12): 2987-2994.
[32] LIU H X, HUANG Y Y, YUAN L,. Isothermal crystallization kinetics of modified bamboo cellulose/PCL composites[J]. Carbohydrate Polymers, 2010, 79(3): 513-519.
[33] MALEK J. The applicability of Johnson-Mehl-Avrami model in the thermal analysis of the crystallization kinetics of glasses[J]. Thermochimica Acta, 1995, 267(95): 61-73.
[34] LIU X, ZHUANG K Y, LIN S,. Determination of supercooling degree, nucleation and growth rates, and particle size for ice slurry crystallization in vacuum[J]. Crystals, 2017, 7(5): 128.
Non-isothermal crystallization kinetics of dynamic ice slurry production by vacuum method
LIU Xi, ZHUANG Kunyu, HUANG Cheng, LI Xuelai
(School of Chemical Engineering, Fuzhou University, Fuzhou 350116, Fujian, China)
Ice slurry treated with sodium chloride was produced by vacuum method. The feasibility of describing the crystallization behaviors of ice slurry based on the non-isothermal crystallization kinetic model, Jeziorny and Mo method, was theoretically proved.The relationships between the crystallization time and the ice packing fraction (IPF) were measured and the non-isothermal crystallization kinetic equations were developed. Experimental results indicated that the non-isothermal crystallization kinetics of ice slurry formation fit the Jeziorny and Mo model very well.The values of the Jeziorny exponentwere between 0.473 and 0.525, indicating that the crystallization mechanisms were almost the same for different experimental conditions and the growth pattern of ice crystals was flake thickening.The change trends of the crystallization kinetic parameters,c, the crystallization time,0.25, and the cooling rate function,(), revealed that high cooling rate was beneficial to promote the formation of ice slurry and sodium chloride inhibited the growth of ice crystals.
ice slurry; crystallization; kinetics; vacuum ice; kinetic modeling
10.11949/j.issn.0438-1157.20170336
TK 02
A
0438—1157(2017)08—3071—11
李学来。第一作者:刘曦 (1983—),女,博士,讲师。
国家基础科学人才培养基金项目(J1103303);福建省中青年教师教育科研项目(JA14053)。
2017-03-31收到初稿,2017-06-10收到修改稿。
2017-03-31.
LI Xuelai, lxl6632@sina.com
supported by the National Natural Science Foundation of China (J1103303) and the Program of Young Teacher Education and Research of Fujian Province(JA14053).
